独立性检验考向解析与备考建议
2023-02-24秦文波
秦文波
(重庆市璧山区教师进修学校)
独立性检验是高中阶段所学的一种检验方法,是近年来高考的考查热点.为了更好地复习备考,本文就独立性检验的考向进行诠释,并结合新课标要求给出备考建议.
1 考向解析
1.1 等高条形图分析
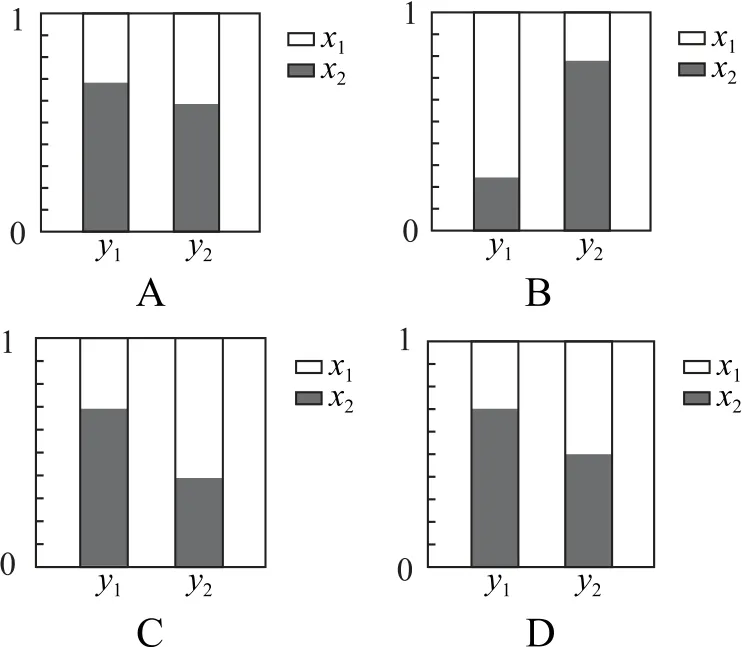
例1在下面频率等高条形图中,两个分类变量x与y关系最强的是( ).
1.2 列联表分析
例2假设两个分类变量x与y的2×2列联表如表1所示.
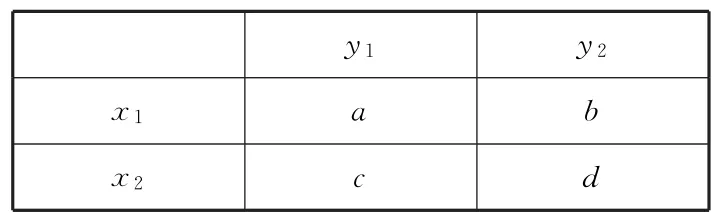
表1
对于以下数据,对同一样本能说明x与y有关系的可能性最大的一组为( ).
A.a=20,b=30,c=40,d=50
B.a=50,b=30,c=30,d=40
C.a=30,b=60,c=20,d=50
D.a=50,b=30,c=40,d=30
1.3 统计量K2 的计算
例3在研究色盲与性别的关系调查中,调查了男性50人,其中有20人患色盲,调查的60个女性中15人患色盲,则变量K2的值约为( ).
A.1.60 B.2.83 C.2.712 D.6.004
列出2×2列联表如表2所示.
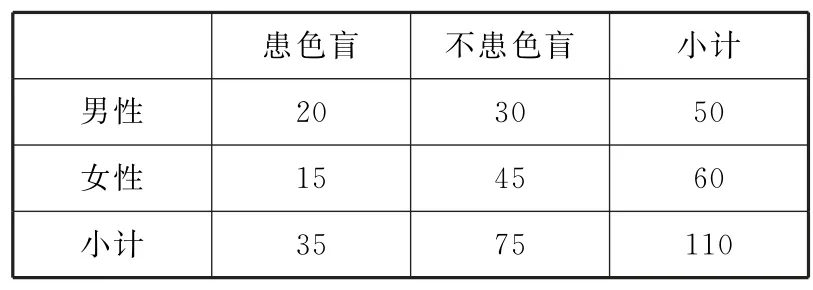
表2
故选B.
1.4 独立性检验的概念及辨析
例4有关独立性检验的四个命题,其中为假命题的是( ).
A.两个分类变量的2×2列联表中,对角线上数据的乘积相差越大,说明这两个变量有关系的可能性就越大
B.对分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”的可信程度越小
C.从独立性检验可知:有95%把握认为秃顶与患心脏病有关,我们说某人秃顶,那么他有95%可能患有心脏病
D.从独立性检验可知:有99%的把握认为吸烟与患肺癌有关,是指在犯错误的概率不超过1%前提下认为吸烟与患肺癌有关
1.5 独立性检验解决实际问题
例5(2022年全国甲卷文17,节选)甲、乙两城之间的长途客车均由A和B两家公司运营,为了解这两家公司长途客车的运行情况,随机调查了甲、乙两城之间的500个班次,得到列联表(如表3).
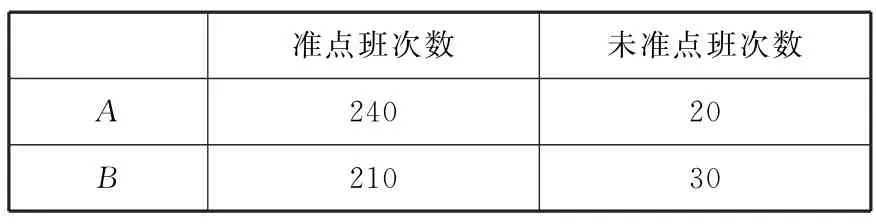
表3
能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关?
1.6 独立性检验与其他知识交会问题
例6为了检测某种抗病毒疫苗的免疫效果,需要进行动物与人体试验,研究人员将疫苗注射到200只小白鼠体内,一段时间后测量小白鼠的某项指标值,按[0,20),[20,40),[40,60),[60,80),[80,100]分组,绘制频率分布直方图如图1所示,试验发现小白鼠体内产生抗体的共有160只,其中该项指标值不小于60的有110只.假设小白鼠注射疫苗后是否产生抗体相互独立.
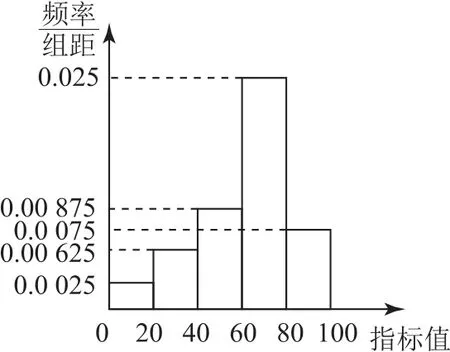
图1
(1)请根据α=0.05的独立性检验,判断能否认为注射疫苗后小白鼠产生抗体与指标值不小于60有关.
(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的40只小白鼠进行第二次注射疫苗,结果又有20只小白鼠产生抗体.
(ⅰ)用频率估计概率,求一只小白鼠注射2次疫苗后产生抗体的概率p;
(ⅱ)以(ⅰ)中确定的概率p作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,记n个人注射2次疫苗后产生抗体的数量为随机变量X.试验后统计数据显示,当X=90时,P(X)取最大值,求参加人体接种试验的人数n及E(X).
在[0,20)内有0.0025×20×200=10只;
在[20,40)内有0.00625×20×200=25只;
在[40,60)内有0.00875×20×200=35只;
在[60,80)内有0.025×20×200=100只;
在[80,100]内有0.0075×20×200=30只.
由题意,有抗体且指标值小于60的有50 只;而指标值小于60的小白鼠共有10+25+35=70只,所以指标值小于60且没有抗体的小白鼠有20只.同理,指标值不小于60且没有抗体的小白鼠有20只,故列联表(单位:只)如表4所示.
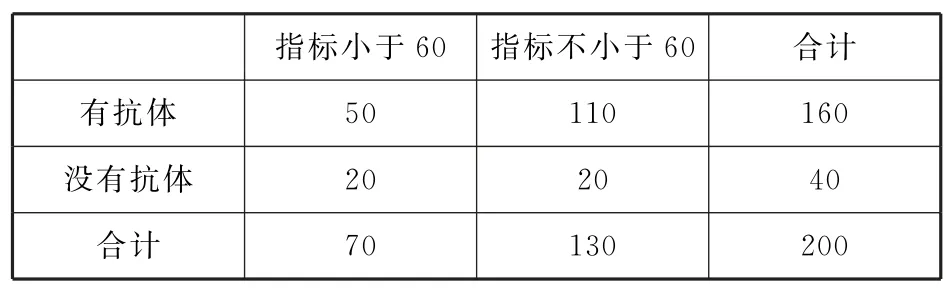
表4
零假设为H0:注射疫苗后小白鼠产生抗体与指标值不小于60无关联.
根据列联表中数据,得
根据α=0.05 的独立性检验,推断H0不成立,即认为注射疫苗后小白鼠产生抗体与指标值不小于60有关,此推断犯错误的概率不大于0.05.
(2)(ⅰ)令事件A为“小白鼠第一次注射疫苗产生抗体”,事件B为“小白鼠第二次注射疫苗产生抗体”,事件C为“小白鼠注射2次疫苗后产生抗体”.
记事件A,B,C发生的概率分别为P(A),P(B),P(C),则
所以一只小白鼠注射2 次疫苗后产生抗体的概率为0.9.
(ⅱ)由题意,知随机变量X~B(n,0.9),则
当接种人数为99 时,E(X)=np=99×0.9=89.1;当接种人数为100 时,E(X)=np=100×0.9=90.
2 备考建议
2.1 要准确理解基础知识
本部分内容的基础知识包括:2×2列联表、等高条形图、统计量K2、独立性检验的概念、基本思想以及操作步骤等,这些都是高考重点考查的内容,需要准确理解并牢固掌握.
2.2 要熟练掌握基本方法
学生要能快速且准确地列出2×2列联表并画出等高条形图,要能根据等高条形图准确列出2×2列联表,要熟练独立性检验的操作步骤和结果的表述方式.
2.3 要不断提高运算能力
关于统计量K2的观测值的获得需要较大的运算量,我们平时要提高自己的运算求解能力,计算时最好能提取公因数或借助平方差公式因式分解后再约分化简求解,结果最好先以分式形式呈现,再根据题目要求保留相应小数点位数.
2.4 要重视练习的质和量
平时的练习题要在重视基础的前提下适当顾及广度、深度和难度,练习题尽量选取各省市或名校模拟试题以及高考真题.
2.5 要深入理解独立性检验的基本思想
独立性检验本质上是对两个分类变量独立性的假设检验,基本思路:先假设两个分类变量独立,再在给定显著性水平下计算统计量K2的观测值并与临界值比较,最后根据比较结果作出拒绝假设或接受假设的概率解释.
2×2列联表、等高条形图和统计量K2的观测值可以判断两个分类变量是否有关系.2×2列联表对角线乘积相差越大,则两个分类变量有关系的可能性越大;等高条形图下方颜色高度相差越大,则两个分类变量有关系的可能性越大;统计量K2的观测值越大,则两个分类变量有关系的可能性越大.
在给定显著性水平α的条件下,利用统计量K2的观测值k与α对应的临界值k0的大小关系可以从概率的角度判断两个分类变量是否有关系.若k≥k0,则可表述为能在犯错误的概率不超过α的前提下认为这两类分类变量有关系;有1-α(百分比)的把握认为这两个分类变量有关系.若k<k0,则可表述为不能在犯错误的概率不超过α的前提下判定这两个分类变量有关;没有1-α(百分比)的把握认为这两个分类变量有关.
3 备考练习
练习1(多选题)为了增强学生的身体素质,某校将冬天长跑作为一项制度固定下来,每天大课间例行跑操.为了调查学生喜欢跑步是否与性别有关,研究人员随机调查了相同人数的男、女学生,发现男生中有80%喜欢跑步,女生中有40%不喜欢跑步,且有95%的把握判断喜欢跑步与性别有关,但没有99%的把握判断喜欢跑步与性别有关,则被调查的男、女学生的总人数可能为( ).
A.120 B.130 C.240 D.250
答案AB.
练习2某种常见疾病可分为Ⅰ,Ⅱ两种类型.为了了解该疾病类型与地域、初次患该疾病的年龄(以下简称初次患病年龄)的关系,在甲、乙两个地区共随机抽取100名患者调查其疾病类型及初次患病年龄,得到的数据如表5所示.
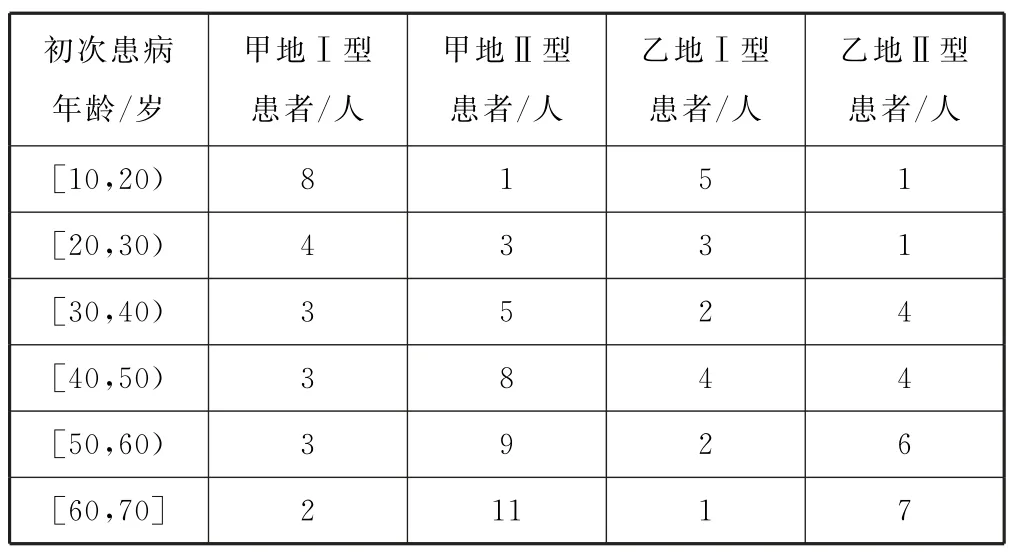
表5
记初次患病年龄在[10,40)的患者为低龄患者,初次患病年龄在[40,70]的患者为高龄患者.根据表5中数据,解决以下问题:
(1)将以下列联表(表6和表7)补充完整,并判断地域、初次患病年龄这两个变量中哪个变量与该疾病的类型有关联的可能性更大(直接写出结论,不必说明理由).
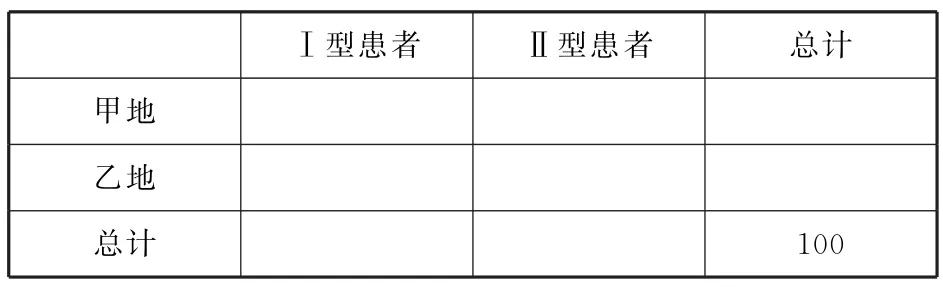
表6
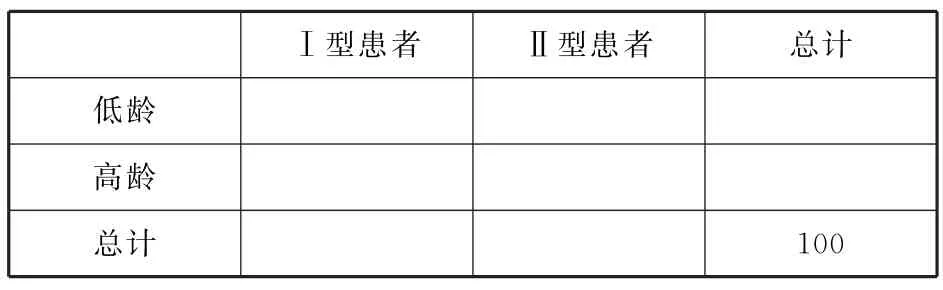
表7
(2)记(1)中与该疾病的类型有关联的可能性更大的变量为X.问:是否有99%的把握认为该疾病的类型与X有关?
答案(1)列联表略,初次患病年龄与该疾病的类型有关联的可能性更大.
(2)有99%的把握认为该疾病类型与初次患病年龄有关.
练习3为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取100名学生,将他们的竞赛成绩(满分为100 分)分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],得到如图2所示的频率分布直方图.
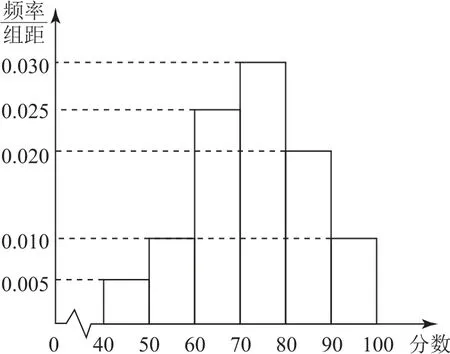
图2
(1)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表),并估计这100 名学生成绩的中位数(精确到0.01);
(2)在抽取的100名学生中,规定:竞赛成绩不低于80分为“优秀”,竞赛成绩低于80分为“非优秀”.
(ⅰ)请判断是否有99%的把握认为“竞赛成绩是否优秀与性别有关”?
(ⅱ)求出等高条形图需要的数据,并画出等高条形图(按图3中“优秀”和“非优秀”所对应阴影线画),利用条形图判断竞赛成绩优秀与性别是否有关系?
图3
答案 (1)平均成绩73,中位数73.33.
(2)(ⅰ)略,没有;(ⅱ)略,有.
本文可能用到的参考公式及数据:

表8
(完)
