国产原子钟频率稳定度评估分析

陈汗龙，董 哲，周真帆，郑晓雪

国产原子钟频率稳定度评估分析

陈汗龙，董 哲，周真帆，郑晓雪

（北京卫星导航中心，北京 100094）

针对单一频率稳定度测量方法中存在周期过长或测量精度不达标的问题，提出使用2种测量方法结合的国产原子钟频率稳定度评估分析方法：一是利用相位噪声测量仪5120A对原子钟的相位噪声和短期稳定度进行测量；二是利用多通道时间间隔计数器经数据提取、预处理和“3σ”粗差剔除后，分别用阿伦方差、重叠阿伦方差和重叠哈达玛方差对多台原子钟长期稳定度进行计算和分析。实验结果表明，该方法既能满足测量精度要求，又可满足测量环境统一性的要求，且可大幅缩减多台钟的测量时长，验证了测量方法的可行性、有效性。

原子钟；阿伦方差；频率稳定度；相位噪声；评估分析

0 引言

原子钟（或频率源）的主要任务就是输出连续恒定的频率信号。作为一种电子设备，原子钟实际输出频率并非一个固定值，受到其内部电路噪声或外部环境扰动等影响，实际输出频率会呈现出随机起伏的特征[1-2]。频率稳定度就是用来描述频率源输出的频率受噪声影响程度的大小，表示信号在给定时间段内频率或相位偏差相对于平均频率或平均相位偏差的波动[3-6]，是衡量频率源性能的重要指标之一。

式中()为单边带相位噪声，大小等于噪声信号调制的单边带功率和载波功率之比。

时域频率稳定度从时域的角度把受噪声影响的输出频率用一个时间函数来描述，常用阿伦方差（Allan variance）、重叠阿伦方差（overlapping Allan variance）或哈达玛方差（Hadamard variance）来表示。阿伦方差表达式为[1,6]

如果为了计算天稳、周稳或更长的频率稳定度结果，则需要大量的采样数据，导致测量时间过长。为了在有限的测量时间内最大限度地利用有效数据，并且获得较好的统计置信度，有必要采用迭代取样法进行分析计算。重叠阿伦方差是普通阿伦方差的一种特殊形式，将取样数为的时差测量数据形成（2个）频率差分来最大限度利用有效数据，大幅减少测量时长，即有[1]

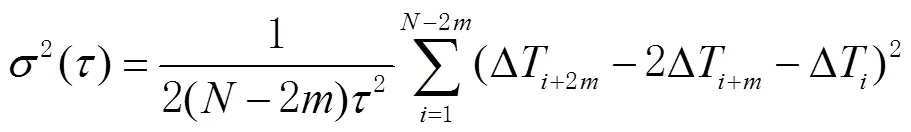
哈达玛方差是基于哈达玛变化的一种时域频率稳定度计算方法。哈达玛变换比Allan方差的分辨率高，优点在于对频率源的线性频率漂移不敏感，也常被用于原子钟稳定度的评价和计算，即[5,7-8]

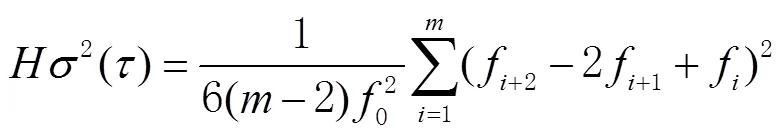
同样，在实际应用中对于测量的相位数据常转换为

与哈达玛方差对应特殊形式的重叠哈达玛方差为

将取样数为的时差测量数据形成（3个）频率差分的重叠哈达玛方差，同样缩减了测量周期。

1 基准频率标准

在频率稳定度的测量中，通常需要一个参考频率源作为基准频率标准，并且要求这个参考频率源的稳定度比被测频率标准高一个量级以上，否则无法科学计算出被测频率标准的真实稳定度[9-11]。该测试所选用参考频率源主要性能指标如表1所示。

表1 参考频率源主要性能指标

参考频率源具有较好的频率稳定度、较低的相位噪声特性，其长期和短期频率稳定度均比被测原子钟出厂指标高一个量级以上，可作为基准频率标准进行测量。将参考频率源和被测原子钟放置在恒温（20±0.2℃）恒湿环境下连续稳定运行一段时间后，对实际输出频率信号和脉冲信号进行采集和测量，分别计算其频域频率稳定度和时域频率稳定度。被测国产原子钟分别被命名为A-01、A-02、B-01、B-02、C-01和C-02。

2 频域频率稳定度实测

利用单边带相位噪声()去评价和描述被测原子钟的频域频率稳定度，它是指在偏离载频傅氏频率处，1 Hz带宽的相位噪声调制单边带功率与载波功率之比，单位为dBc/Hz，表征了频率源输出的标准频率信号附近相位噪声的分布情况。测量仪器选用相位噪声测量仪5120A，测量精度为±1.0 dB，6台原子钟实际相位噪声测量结果如图1～图6所示，横坐标为偏差频率，纵坐标为单边带相位噪声。

对国产原子钟相位噪声实测数据汇总，得到如表2所示结果。

图1 A-01（氢钟）相位噪声实测

图2 A-02（氢钟）相位噪声实测

图3 B-01（氢钟）相位噪声实测

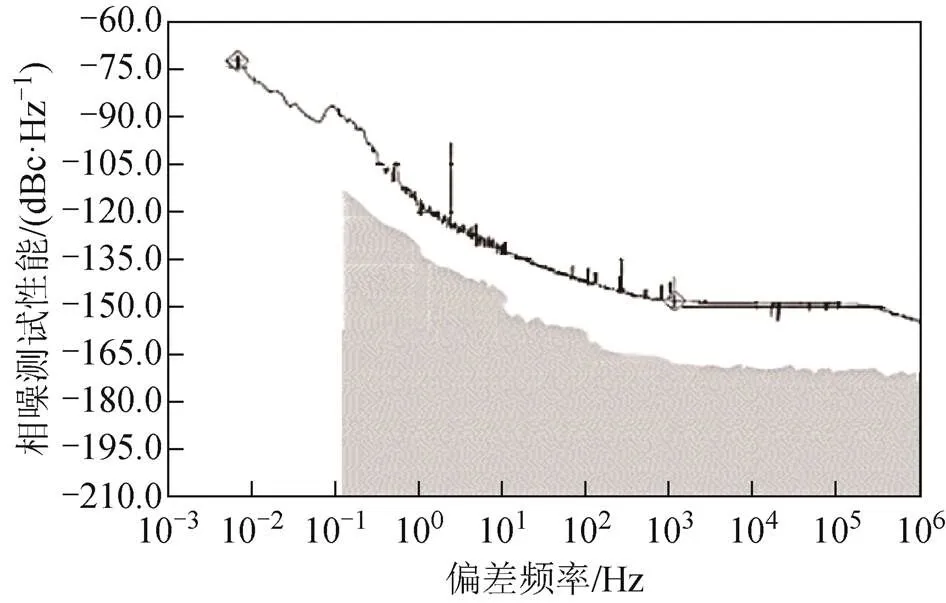
图4 B-02（氢钟）相位噪声实测

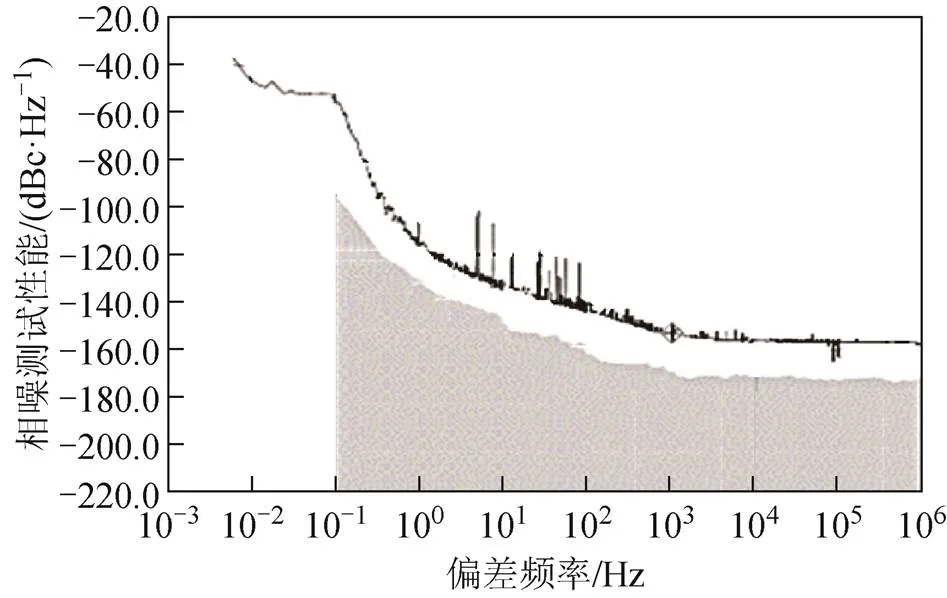
图5 C-01（铯钟）相位噪声实测

图6 C-02（铯钟）相位噪声实测

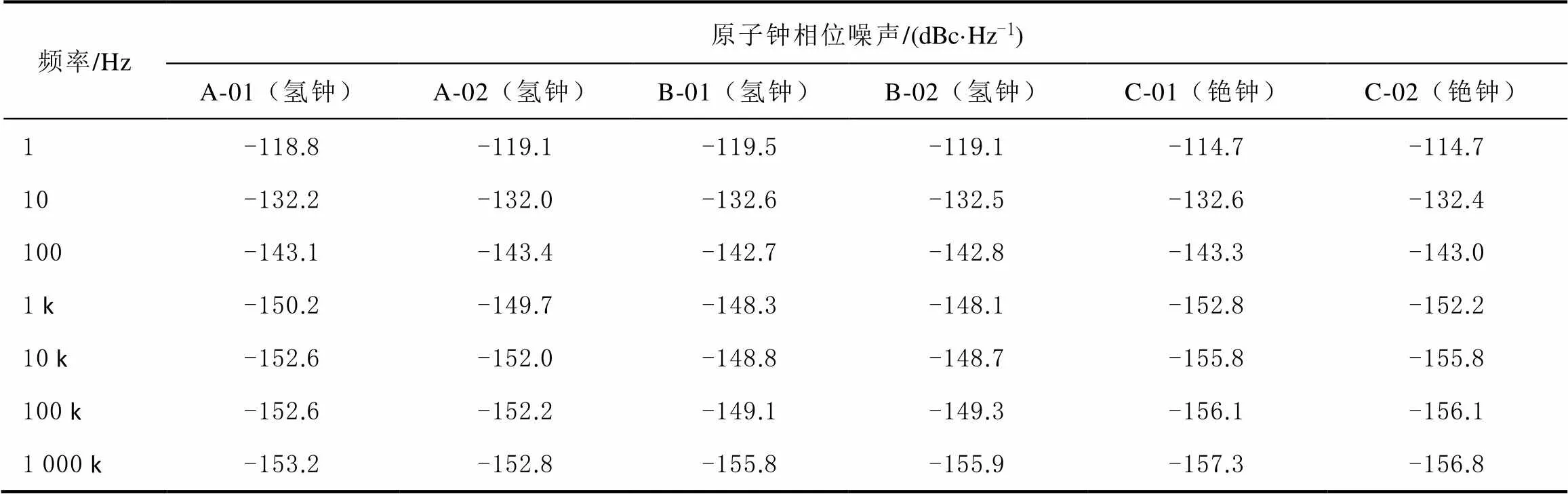
表2 国产原子钟相位噪声测量结果汇总

3 时域频率稳定度实测

采取2种方式同步测量。

一是利用相位噪声测量仪5120A直接测量短期时域频率稳定度结果。该方法短期频率稳定度测量精度较高；缺点是该类型设备通常只有一路10 MHz信号比对通道，同一时间仅支持单台原子钟频率稳定度的测量，对多台钟的天以上稳定度测量周期过长，不同时间的测量环境也会发生一定变化。因此，可使用该方法逐一对国产原子钟的短期（10000 s以下）频率稳定度进行测量，测量结果如表3所示。

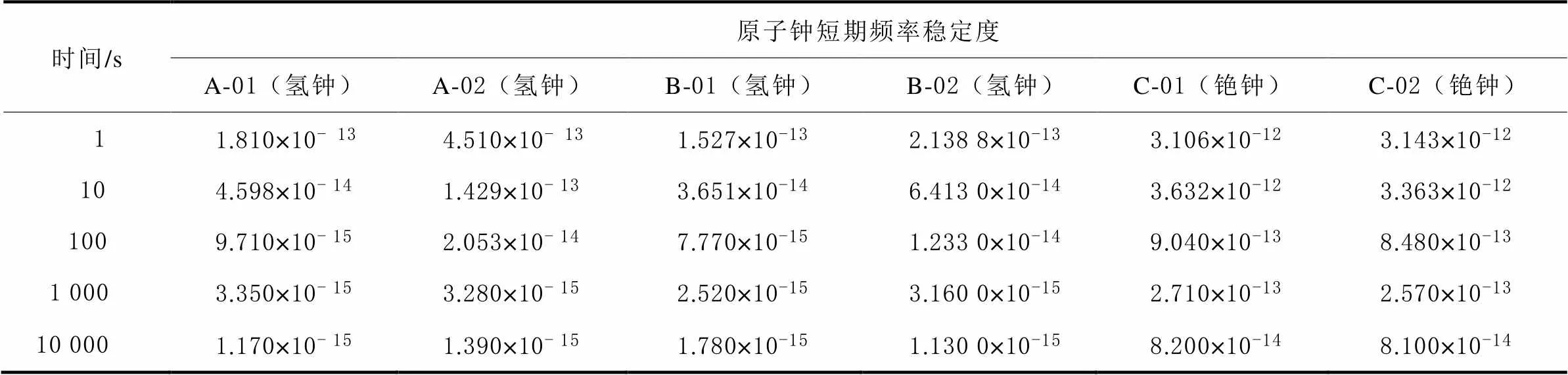
表3 相位噪声测量仪短期频率稳定度测量结果

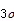
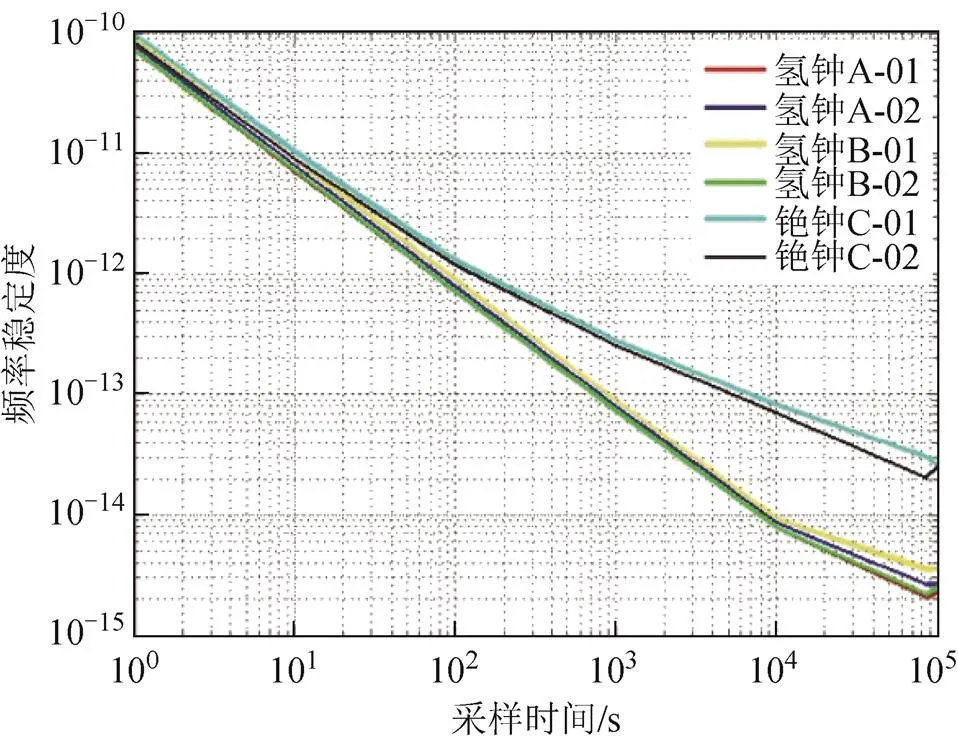
图7 时间间隔计数器标准阿伦方差结果

图8 时间间隔计数器重叠阿伦方差结果

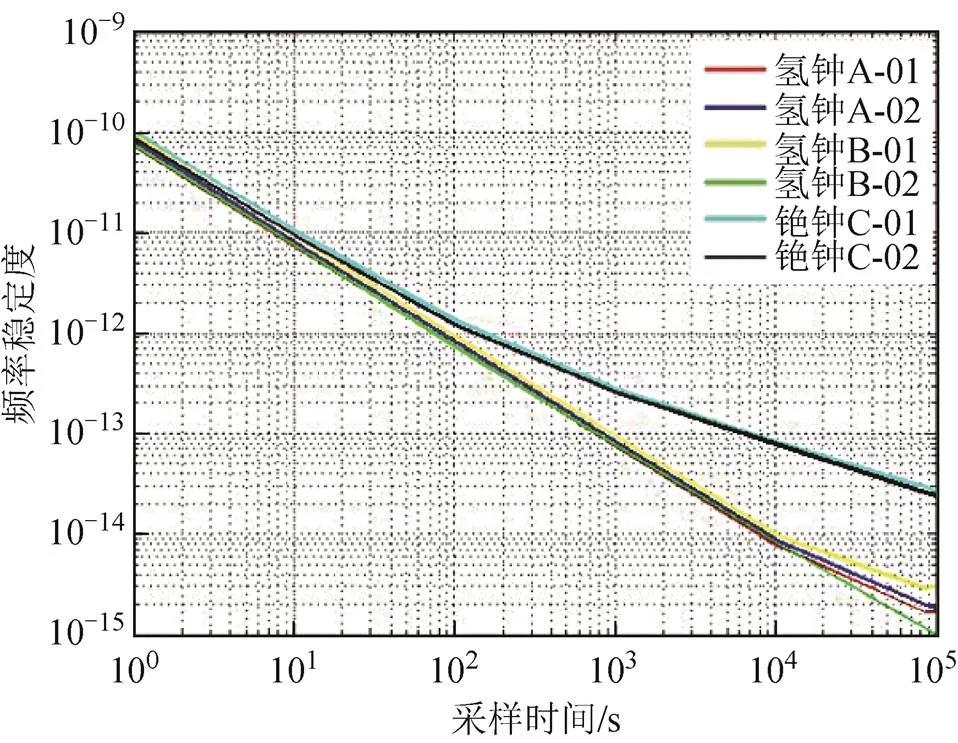
图9 时间间隔计数器重叠哈达玛方差结果

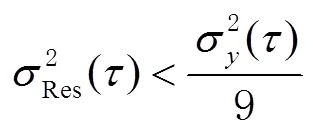
对国产原子钟天稳定度和10万s稳定取阿伦方差、重叠阿伦方差和重叠哈达玛方差均值，可得到综合频率稳定度评估分析结果。

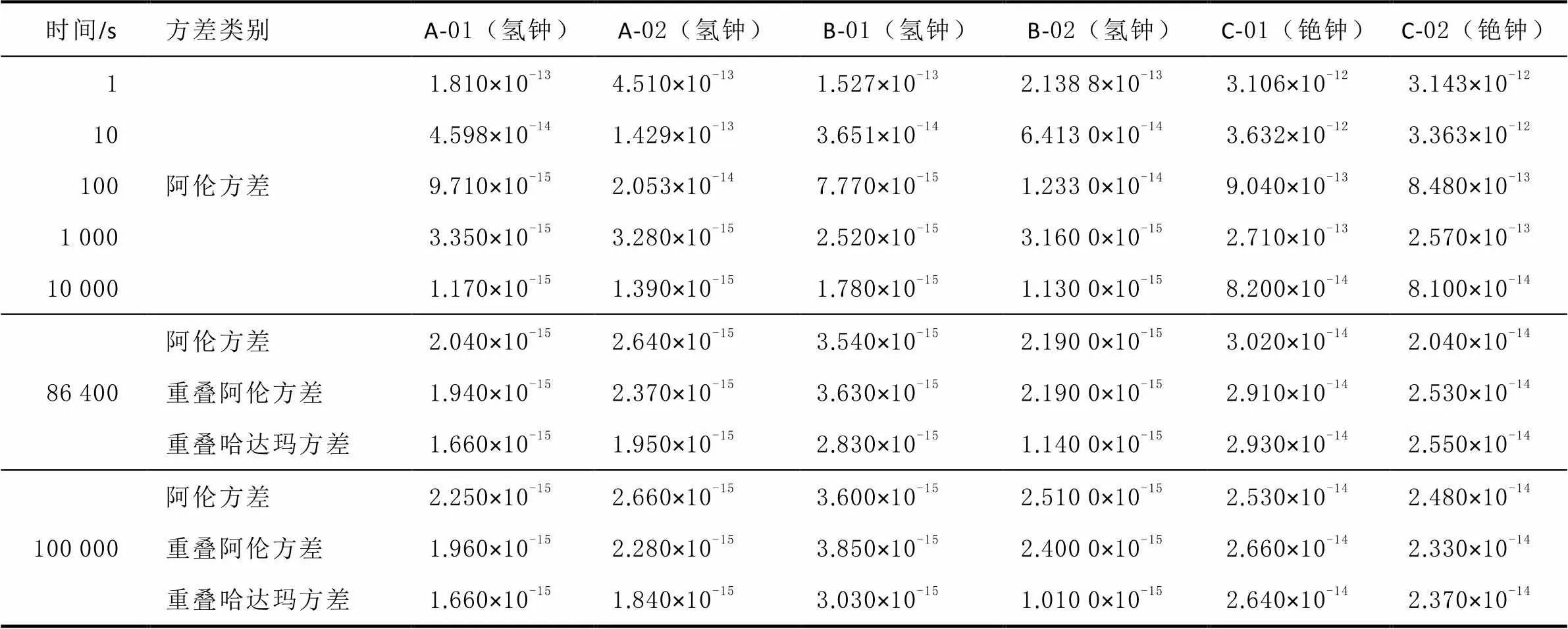
表4 国产原子钟时域频率稳定度综合分析

对实验实测数据进行分析：一是时域频率稳定度上，1～10万s范围内国产氢原子钟较铯原子钟均高1个数量级，氢原子钟1000 s稳至10万s稳可达10-15量级，与出厂设计指标一致。国产铯原子钟短期稳定度不如氢原子钟，但万秒稳和天稳可达10-14量级，且铯钟的优势在于长期运行中不存在明显的频率漂移；二是频域频率稳定度上，国产原子钟单边带相位噪声相差不大，例如在偏离10 Hz频率处均低于-132 dBc/Hz，较为优质；三是评估方法上，标准阿伦方差、重叠阿伦方差和重叠哈达玛方差均可对时域频率稳定度进行有效计算和评估，结果趋于一致，其中重叠哈达码方差计算频率稳定度结果较优，原因在于它可消除部分线性频率漂移误差，分辨率高于阿伦方差，而重叠阿伦方差与阿伦方差计算结果相差不大，但采取“重叠”的方法可大幅缩减测量时长。综合2种测量和计算方法，各原子钟频率稳定度综合分析结果如图10所示。

4 结束语

本文从时域和频域角度对频率稳定度计算原理进行了分析，采用相位噪声测量仪和多通道时间间隔计数器同步对国产原子钟频率稳定度进行了评估分析，实验结果表明：国产氢原子钟10万s和天稳定度均可达10-15量级，国产铯原子钟10万s和天稳定度均可达10-14量级，在1～10万s范围的频率稳定度上，氢原子钟比铯原子钟普遍高一个量级以上，但天稳以上二者指标差距逐渐缩小，符合氢钟与铯钟的特性；实验还验证了结合使用相位噪声测量仪和多通道时间间隔计数器2种方式同步开展频率稳定度测量的可行性、有效性，可使用该方法对多台原子钟进行同步测量，既满足了测量精度又缩短了测量周期，具有实际借鉴价值。

图10 原子钟频率稳定度综合分析结果

[1] 童宝润. 时间统一技术[M]. 北京: 国防工业出版社, 2004: 278-296.

[2] 美国电气电子工程师学会. 基本频率和时间计量学用物理量定义随机不稳定性: IEEE 1139—2008[S]. IEEE, 2008.

[3] 曾庆化. 全球导航卫星系统[M]. 北京: 国防工业出版社, 2014: 1-39.

[4] 董哲, 陈汗龙, 欧阳文, 等. 卫星导航系统星载钟时域频率稳定度探讨[J]. 现代导航, 2022, 13(4): 251-257.

[5] 李孝辉. 时间频率信号的精密测量[M]. 北京: 科学出版社, 2010: 16-36.

[6] 贾小林, 冯来平, 毛悦, 等. GPS星载原子钟性能评估[J]. 时间频率学报, 2010, 33(2): 115-120.

[7] 钦伟瑾, 葛玉龙, 杨旭海. 伽利略星载被动型氢原子钟性能评估[J]. 仪器仪表学报, 2018, 39(10): 93-99.

[8] 赵丹宁. GLONASS星载钟性能分析[J]. 时间频率学报, 2020, 43(1): 66-71.

[9] 丁毅涛, 郭美军. 基于不同机构钟差产品的GNSS星载钟性能分析与评估[J]. 时间频率学报, 2020, 43(1): 72-84.

[10] 韩有文. Galileo卫星星载原子钟性能分析[J]. 导航定位学报, 2020, 8(1): 54-58.

[11] 杨玉峰, 彭勇, 刘梦晗, 等. BDS-3在轨卫星钟性能评估与分析[J]. 导航定位学报, 2021, 9(1): 53-60.

[12] 王宇谱, 吕志平, 王宁. BDS星载原子钟长期性能分析[J]. 测绘学报, 2017, 46(2): 157-169.

[13] 艾青松. GNSS星载原子钟时频特性分析及钟差预报算法研究[D]. 长安大学, 2017: 11-35.

[14] 白杉杉, 董绍武, 赵书红, 等. 主动型氢原子钟性能监测及评估方法研究[J]. 天文学报, 2018, 59(6): 58-68.

[15] 刘峰宇, 王宇谱, 李锡瑞. 国产SOHM-4型氢钟长期性能分析[J]. 导航定位学报, 2020, 8(5): 102-106,116.

[16] 张军, 王向磊, 王路生, 等. 国产小铯钟比测结果分析[J]. 时间频率学报, 2018, 41(3): 162-170.

[17] 伍贻威, 杨斌, 肖胜红, 等. 原子钟模型和频率稳定度分析方法[J]. 武汉大学学报(信息科学版), 2019, 44(8): 1226-1232.

[18] 徐荣, 赵金峰, 田湘, 等. 北斗高精度时间同步技术方案[J]. 导航定位学报, 2023, 11(1): 154-158.

[19] 陈亮, 展昕, 许磊, 等. BDS授时性能分析与接收机DCB估计[J]. 导航定位学报, 2023, 11(1): 53-59.

[20] 郭海荣, 杨元喜. 导航卫星原子钟时域频率稳定性影响因素分析[J]. 武汉大学学报(信息科学版), 2009, 34(2): 218-221.

Evaluation and analysis of frequency stability for domestic atomic clocks

CHEN Hanlong, DONG Zhe, ZHOU Zhenfan, ZHENG Xiaoxue

（Beijing Satellite Navigation Center, Beijing 100094, China）

Aiming at the problem that the measurement period is too long or the measurement precision cannot satisfy the standard requirement in the single frequency stability measurement, the paper proposed an evaluation and analysis method of frequency stability for domestic atomic clocks combined with two means: firstly, phase noise and short-term stability of atomic clock were measured by phase noise meter 5120A; second, after data extraction, pre-processing and “3σ” gross error elimination using multi-channel time interval counter, Allern variance, overlapping Allern variance and overlapping Hadamard variance were used to calculate and analyze the long-term stability of multiple atomic clocks. Experimental result showed that the proposed method could not only meet the requirement of measuring precision, but also meet the unity requirement of measuring environment, and greatly reduce the measurement time of multiple clocks, which verifies its feasibility and effectiveness.

atomic clock; Allan variance; frequency stability; phase noise; evaluation and analysis

陈汗龙，董哲，周真帆，等. 国产原子钟频率稳定度评估分析[J]. 导航定位学报, 2023, 11(6): 28-33.（CHEN Hanlong, DONG Zhe, ZHOU Zhenfan, et al. Evaluation and analysis of frequency stability for domestic atomic clocks[J]. Journal of Navigation and Positioning, 2023, 11(6): 28-33.）DOI:10.16547/j.cnki.10-1096.20230604.

P228

A

2095-4999(2023)06-0028-05

2023-03-10

陈汗龙（1988—），男，湖北十堰人，硕士，工程师，研究方向为卫星导航和时间频率。