基于磁链预测的永磁直驱风力发电机SVM-DTC 技术
2023-02-23单立宇张兰红陈小海
单立宇,张兰红,陈小海
(1.江苏大学电气信息工程学院,江苏镇江 212013;2.盐城工学院电气工程学院,江苏盐城 224051;3.江苏金风科技有限公司,江苏盐城 224051)
风能作为一种清洁、可再生的绿色能源,其开发利用对于减少传统化石能源消耗和减轻环境污染有重大意义,因此风力发电正被越来越多的国家所重视[1]。永磁直驱风力发电机将风力机与永磁同步发电机直接相连,无需齿轮箱,具有损耗低、可靠性高等优势[2-3],已成为风力发电的主流机型。直接转矩控制(Direct Torque Control,DTC)技术不需要大量坐标变换,将转矩直接作为被控制量,具有结构简单、响应速度快等优点,已被推广应用到永磁直驱风力发电机的控制系统中[4-6]。
然而,传统DTC 技术有着明显不足,一是在开关表控制方式下,只能利用逆变器输出的六个固定非零电压矢量来控制转矩和磁链,无法对定子磁链和转矩进行精确调节;二是采用磁链和转矩滞环控制方式,导致磁链和转矩波动较大[7-9]。
针对传统DTC 技术的不足,文中研究了一种基于定子磁链预测的永磁直驱风力发电机SVM-DTC(Direct Torque Control based on Space Vector Modulation)策略,通过预测算法得到下一个控制周期的磁链矢量,进而求得需要补偿的电压矢量,再结合SVPWM(Space Vector Pulse Width Modulation)可以准确合成任意位置的电压矢量,实现对磁链和转矩的精准控制[10],从而改进永磁直驱风力发电机的控制性能。
1 传统DTC技术
传统DTC 控制是通过滞环控制器和查表法方式选择合适的电压矢量,以实现对磁链和转矩的直接控制[11]。
永磁直驱风力发电机的电磁转矩方程为:

式 中,Te为转矩,pn为极对数,Ls为定子自感,|ψs|、|ψf|分别为定、转子磁链幅值,δ为定、转子磁链的夹角。
由于转子磁链的转速取决于原动机转速,在一个控制周期内可认为 |ψf|保持不变,则由式(1)可知,若 |ψs|为恒定值,那么可以通过改变定、转子磁链夹角δ来调节电磁转矩[12]。由于转子磁链的转动速度是恒定的,因此δ的大小可通过控制定子磁链的旋转来改变。定子磁链方程为:
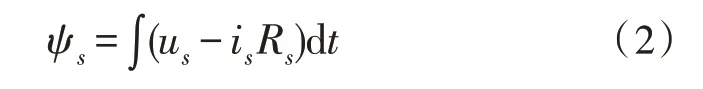
式中,ψs为定子磁链,us为定子电压,Rs为定子电阻,is为定子电流。
忽略定子电阻的影响,由式(2)可得:

由式(3)可知,定子磁链的大小和运动方向都受定子电压矢量的影响,其中所需要的电压矢量由滞环控制器和扇区信号共同决定,通过选择合适的开关电压矢量来控制磁链矢量的幅值在滞环控制器的控制范围内,并沿着特定方向旋转。
图1 所示为传统DTC 中的定子磁链运行轨迹,空间被电压矢量u1-u6分为六个扇区。以定子磁链ψs在Ⅰ扇区为例,若要增大定子磁链幅值,可以选择u2或u6;若要减小定子磁链幅值,则选择u3或u5。假设电机逆时针转动,若要使转矩增大,则选择u2、u3控制定子磁链正向加速;若要使转矩减小,则选择u5、u6控制定子磁链反向加速,可以类推其余扇区情况。

图1 传统DTC控制的定子磁链运行轨迹
综上分析可知,转矩随定子磁链滞环宽度内脉动,因此需要寻求与DTC 技术相结合的新控制算法来取代滞环控制器。
2 基于磁链预测SVM-DTC技术
2.1 基于磁链预测的SVM-DTC控制原理
基于磁链预测的SVM-DTC 系统框图如图2 所示,该控制方法采用磁链预测模块、参考电压矢量模块和SVPWM 模块代替了传统DTC 系统中的滞环控制器和开关表[13]。

图2 基于磁链预测的SVM-DTC系统框图
当PMSG(Permanent Magnet Synchronous Generator)的转速无法跟上给定转速时,Te与转矩参考值会有误差,由转矩方程可知,Te与定转子磁链的夹角δ存在非线性关系,δ的大小可通过控制定子磁链的旋转来改变,因此转矩误差可通过PI 调节器求得磁链变化角Δθ来补偿[14];然后在磁链预测模块中求出定子磁链的增量,再输入到参考电压矢量模块,生成两个参考矢量,送入SVPWM 模块中可发出相应脉冲信号控制变流器通断,进而控制发电机运行。
2.2 定子磁链预测
假设当前采样时刻为k,则定义当前采样周期内的定子磁链为ψs(k),幅值为磁链估算值ψs;下一个采样周期的定子磁链为ψs(k+1),幅值为磁链给定值。第k个和第k+1 个周期中磁链矢量关系图如图3 所示。
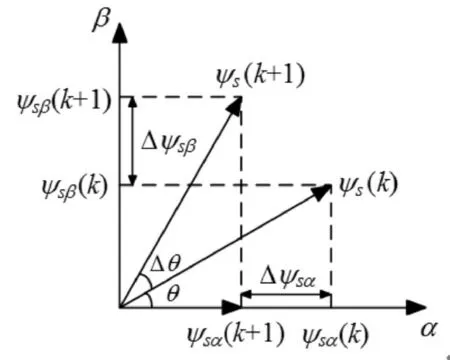
图3 磁链矢量关系图
图3 中,θ为磁链角度,Δθ为磁链的相位变化角。k时刻的定子磁链矢量在两相静止αβ坐标系中表示为:
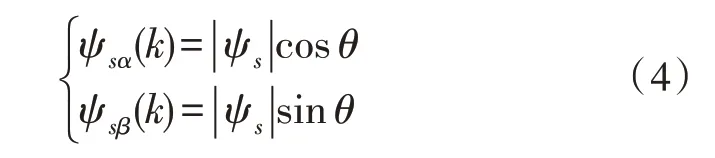
k+1 时刻磁链角度增加Δθ后的定子磁链矢量在两相静止α β坐标系上表示为:
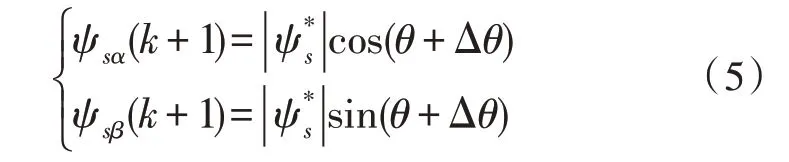
由式(2)可得定子电压的计算公式,由于采样周期Ts很小,微分公式可以转换为:
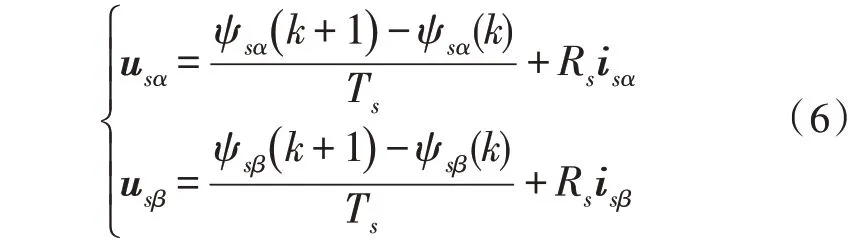
将式(4)、(5)、(6)代入式(7)即可求出期望的参考电压矢量
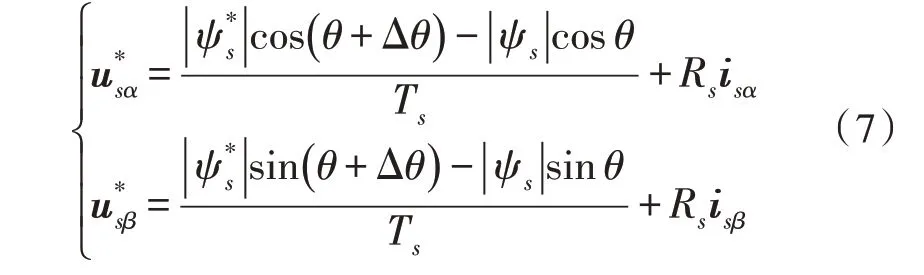
综上分析可知,可以通过参考电压矢量补偿随定子磁链角度的变化而改变的定子磁链,已知电磁转矩可通过改变磁链角度θ来调节,因此采用P(IProportional Integral)调节器对转矩环进行调节,根据转矩差得到定子磁链的相位变化角即可求出下一个周期的磁链。转矩环PI 调节器的输入输出关系表示为:
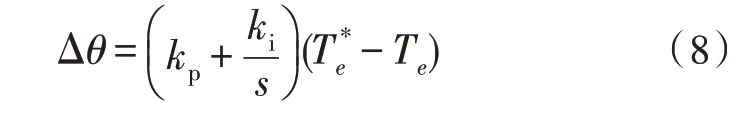
式中,kp、ki分别为比例、积分系数。转矩环PI 调节器的参数对系统性能有重要影响,参数设置不当可能导致较差的转矩响应,影响系统性能。PI参数设置按照先比例、后积分顺序,首先令ki=0,使PI成为纯比例调节,kp从0 逐渐增大,直至转矩波形出现振荡,再将此时的kp减小,直至振荡消失,记录当前kp值,设定PI 的比例系数kp为当前值的60~70%;然后调节ki,先将ki设定为较大值,逐渐减小ki,直至转矩波形振荡,再逐渐增大ki,直至振荡消失,记录当前ki值,设定PI 的积分系数ki为当前值的150~180%,最终kp取值0.002,ki取值2.51 时,测得系统仿真结果较好。
2.3 空间矢量的调制
SVPWM 技术通过控制两个相邻基本电压矢量,依据伏秒平衡法则,合成任意电压矢量us,代替了传统DTC 的查表法[15]。
基本空间电压矢量分布如图4 所示,基本空间电压矢量由八个电压矢量组成,其中u1-u6为非零电压矢量,u0、u7为零矢量,平面被u1-u6分成了六个扇区。
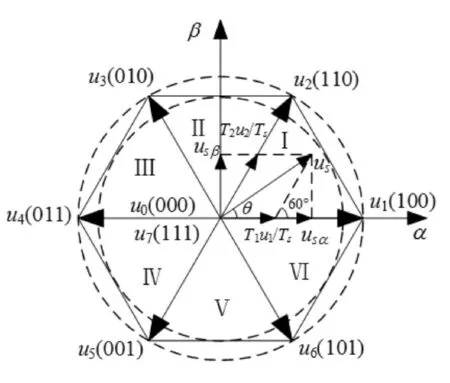
图4 基本空间电压矢量分布图
SVPWM 算法的实现可以分为三个步骤:扇区判断、矢量作用时间计算、矢量切换时间的计算。
2.3.1 扇区判断
定义变量如下:
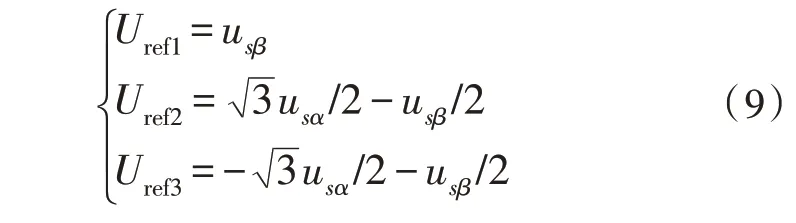
定义:若Uref1>0,则A=1,否则A=0;
若Uref2>0,则B=1,否则B=0;
若Uref3>0,则C=1,否则C=0。
因A、B、C不能同时为1 或0,故有六种组合,令N=A+2B+4C,不同N值时目标电压矢量所在扇区如表1 所示。

表1 N值与扇区号的对应关系
2.3.2 矢量作用时间计算
如图5 所示,若目标电压矢量us位于Ⅰ扇区,那么us可由u1、u2及零电压矢量通过不同作用时间组合得到,利用伏秒平衡法则[16]可得:
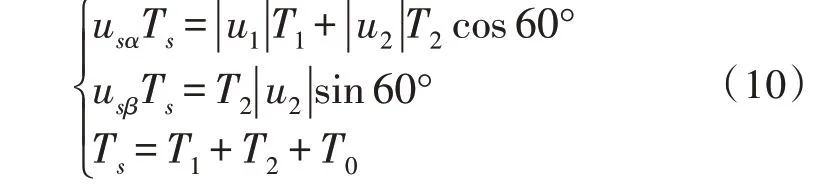
式中,Ts为控制周期,T1、T2、T0分别为电压矢量u1、u2和零矢量的作用时间。
由图5可知,|u1|=|u2|=2Udc/3,则通过式(10)可得:
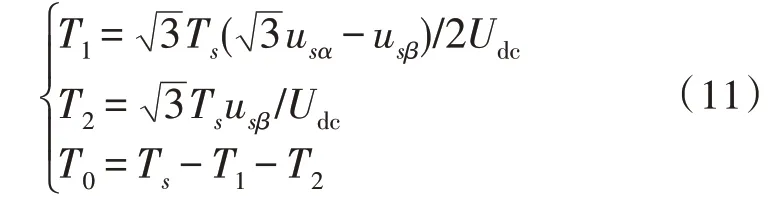
同理可得到其他扇区电压矢量作用时间。为易于分析,定义中间变量x、y、z表示不同扇区的电压矢量作用时间:
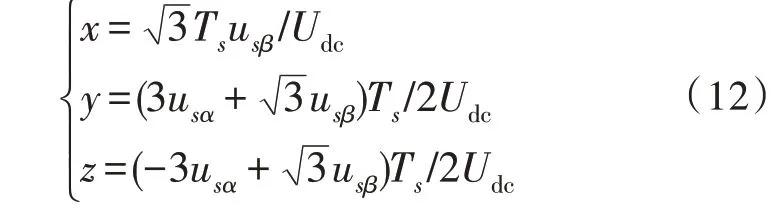
假设先后导通的非零电压矢量作用时间为Tm、Tn,则各扇区相邻矢量作用时间表如表2 所示。

表2 各扇区相邻矢量作用时间表
为避免Tm+Tn>Ts过调制情况的出现[17],用比例缩小算法进行修正:
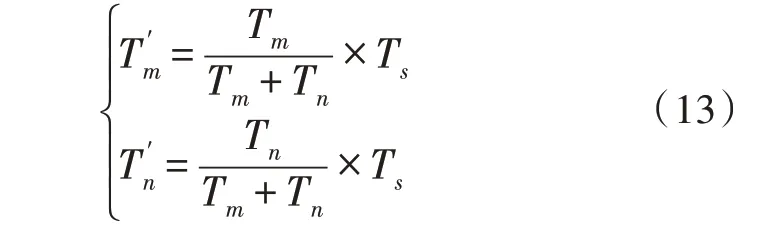
2.3.3 矢量切换时间的计算
计算矢量切换时间以减少开关次数为目标来安排基本矢量作用顺序,每个周期以零矢量开始和结束,并且平均分配零矢量的时间,使PWM 对称,以有效降低谐波分量[18]。
以扇区Ⅰ为例,设Sa、Sb、Sc的导通时刻分别是Ta、Tb、Tc,可得:
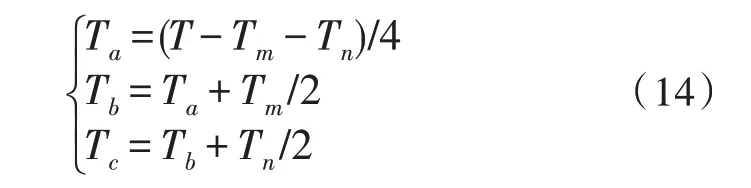
同理可推导其他扇区各矢量切换时间。
3 仿真与分析
根据基于磁链预测永磁直驱风力发电机SVMDTC 系统框图及其控制算法在Matlab/Simulink 中完成其仿真模型的搭建,从而对控制策略进行验证。
仿真电机为隐极式永磁同步发电机,电机相关参数如表3 所示。
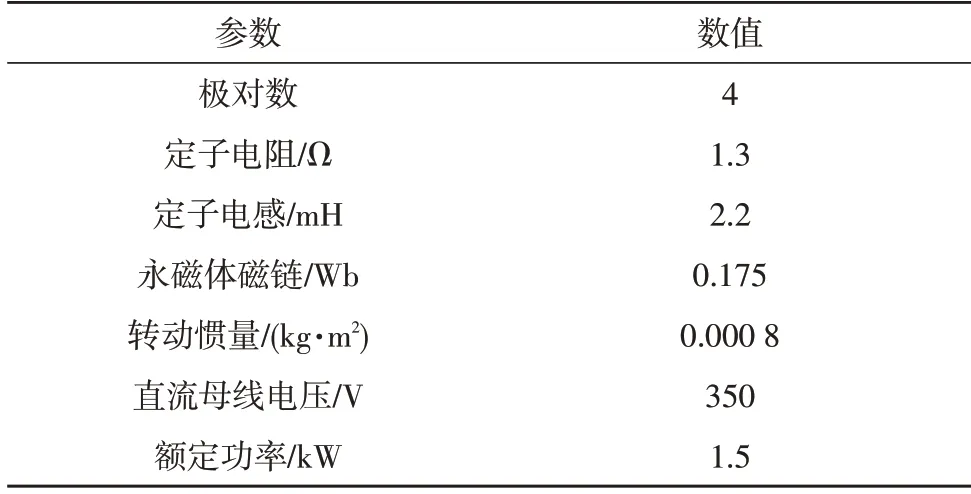
表3 电机参数
仿真环境与传统DTC 控制方法保持一致。风机模型输出初始转速为140 r/min,在0.7 s 时增至190 r/min,转矩由10 N·m 阶跃至21 N·m。根据Simulink 仿真得到定子磁链圆曲线、三相定子电流波形、转矩波形,如图5-7 所示。
将SVM-DTC 的仿真结果和传统DTC 的仿真结果进行对比分析,得到以下结论:
1)从图5 可以看出,磁链幅值约为0.215 Wb,SVM-DTC 方法产生的磁链脉动更小,圆形曲线更加标准。
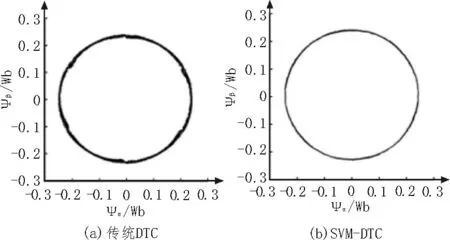
图5 定子磁链圆曲线
2)从图6 对比可以看出,SVM-DTC 方法得到的电流波形更加接近正弦分布,且电流谐波相较于传统DTC 方法明显减小。
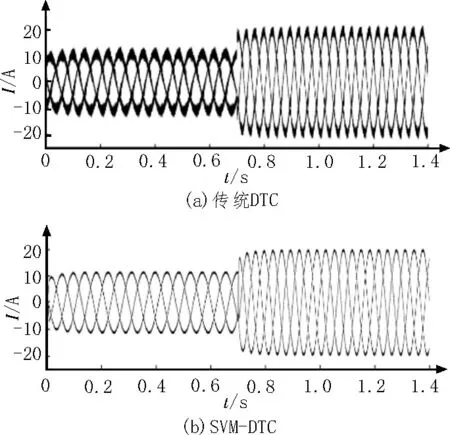
图6 三相定子电流波形
3)从图7 可以看出,当t=0.7 s 时,转矩从10 N·m快速增至21 N·m,SVM-DTC 方法的转矩动态响应更加迅速,且转矩脉动也比传统DTC 小。
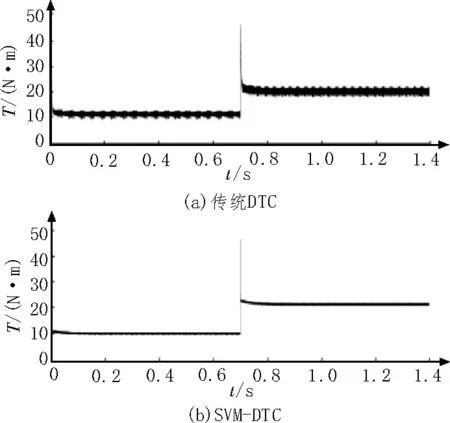
图7 转矩波形
综上所述,采用基于磁链预测SVM-DTC 方法不仅具有传统直接转矩控制动态响应快速的优点,而且大大减弱了电流谐波,使电流波形正弦度更好,同时有效降低了转矩和磁链的脉动。
4 实验分析
为验证基于磁链预测SVM-DTC 方法在实际控制中的可行性,对该控制方法进行实验验证。实验平台由基于TMS320F28377 DSP 芯片的主控制柜、对拖直驱发电机、上位机等组成。
由异步电动机拖动发电机转动模拟风力机,并通过变频器改变异步电动机的转速来模拟风速变化,发电机参数与仿真参数一致,实验工况为电机转速140 r/min,负载转矩10 N·m,实验所得电流波形如图8 所示。从图8 可以看出,发电机发出的三相电流波形的正弦度较好,振幅约为±10 A,与仿真所得的电流波形接近。

图8 三相电流波形
图9 代表α β轴的定子磁链分量的检测结果,由图可知磁链幅值约0.215 Wb,与仿真图5 所示幅值一致,说明实验所测波形正确。
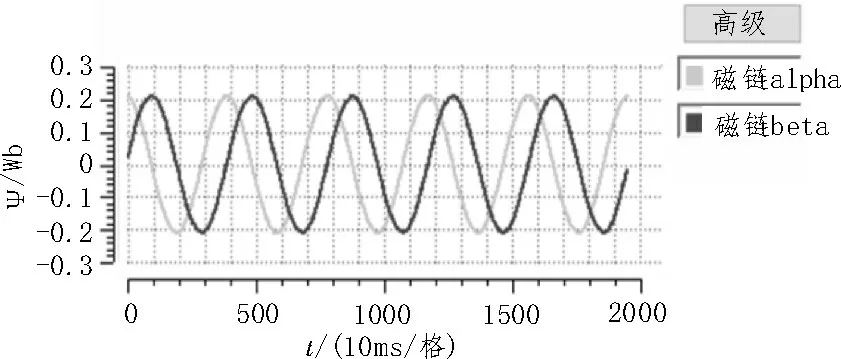
图9 α β 轴的定子磁链分量波形
通过测得的实验波形可以看出,基于定子磁链预测的SVM-DTC 方法的实验结果与仿真结果基本一致,证明了该控制方法应用到永磁直驱风力发电系统中的可行性。
5 结论
文中首先对永磁直驱风力发电机的传统DTC 控制进行了仿真分析,结果显示传统DTC 控制存在转矩和磁链脉动较大等问题。针对该问题,文中研究了一种将定子磁链预测SVPWM 加入到传统DTC 的控制方法,通过对改进算法的仿真和实验研究,对比证明了改进控制方法能明显改善磁链和转矩的脉动,提高系统动稳态特性,并且验证结果也表明了所研究的改进控制方法在系统中的有效性和可行性。
