基于LS-DYNA的某打桩锤机械冲击系统性能仿真

＊王腾 张加翔 于文太 张欣 刘顺庆 张晓馨 张长龙

（1.中国石油大学（华东）海洋物探及勘探开发装备国家工程研究中心 山东 266580 2.青岛科技大学机电工程学院 山东 266061 3.海洋石油工程股份有限公司安装事业部 天津 300450 4.青岛高测科技股份有限公司 山东 266114 5.中机锻压江苏股份有限公司 江苏 226600）

打桩锤是桩基础施工中的重要设备之一，随着桩基的直径和深度的不断增加，对打桩设备的要求越来越高[1-2]。打桩过程中，锤芯、砧座与桩端体承受周期性的冲击载荷，应力和力学关系复杂，难以通过传统计算方法进行分析，借助有限元方法模拟冲击载荷下冲击系统的动力学特性具有重要意义。

Zhou W等人[3]通过摆锤撞击试验，研究了桩在不同撞击条件下的响应和破坏模式；Adegbulugbe O等人[4]提出了一种全尺寸桩冲击性能实验评估方法，模拟了桩的实际工作过程；Qin W等人[5]分析了大直径开口钢桩在冲击荷载下的位移，并探讨了桩锤单次冲击在软土中的偏微分方程，预测了拒锤情况和钢桩的位移。综上，已有文献对冲击载荷下打桩锤冲击系统动力学的研究较少，因此本文基于冲击载荷作用下的打桩锤冲击系统有限元模型，研究不同冲击能量下对砧座应力、桩端位移和冲击力的影响，为打桩锤冲击系统结构设计优化提供参考。

1.基于波动力学冲击过程分析

图1 冲击系统等效模型

锤芯和砧座碰撞过程的本质是应力波产生和传递的过程，古典牛顿碰撞理论忽略了锤芯、砧座及钢桩的形状，应用波动理论分析打桩锤的工作过程能够更加准确地描述各部件的受力状态。在本研究的模型中，砧座被等效为一个具有弹性系数Kh的弹簧，如图1所示。

根据牛顿第二定律和波动理论[6]，可得式（1）：

式中，F为锤芯与砧座的冲击力；Kh为砧座刚度，N·m-1；mc为锤芯阻尼，N·(m·s-1)-1；mz为桩身阻尼，N·(m·s-1)-1；t=0时，v’=v0，v=0，F=0。

由式（1）可得式（2）：

经过拉普拉斯变换后可解得冲击力的表达式（3）：

2.建立模型

本研究将采用Solidworks软件构建的某打桩锤冲击系统三维模型导入ANSYS软件，并运用HyperMesh的高级网格划分功能对该模型进行网格划分，得到如图2所示的有限元模型。锤杆、锤芯、砧座、钢桩和土体材料及其属性见表1和表2所示。由于冲击系统结构和载荷作用的对称特性，为提高仿真计算效率和精度，采用1/4模型进行求解。

表1 金属材料性能参数

表2 土体模型性能参数

冲击过程中，液压系统差动连接（活塞上下端面同时连通高压油），因此对活塞上下端面施加22MPa的压力，如图3所示。

图2 冲击系统有限元模型图

图3 活塞受力示意图

为提高计算效率，本研究将锤芯与砧座的初始间隔定为10mm。在冲击瞬间，锤芯的动能即为其冲击能量，根据动能定理，该打桩锤的最大冲击能量设定为600kJ，锤芯质量为33t。据此计算，锤芯在冲击时的速度为6.03m/s。

3.仿真结果分析

图4 砧座冲击应力时程变化云图

冲击过程不同时刻砧座冲击应力分布云图如图4所示，由图可知，冲击过程中砧座内的应力呈波动状态，应力主要集中于上接触面及其下部区2.0ms。

图5 冲击能量变化曲线图

冲击过程各部件的能量变化情况如图5所示，由图可知，锤芯初始能量为586.18kJ，钢桩最大能量为538.45kJ，因此冲击过程的能量传递效率为91.86%。

4.不同冲击能量的响应分析

通过改变锤芯冲击速度使锤芯具有不同的冲击能量。锤芯冲击速度分别为3m/s、4m/s、5m/s、6m/s，得到桩端位移、最大冲击力以及砧座最大应力如表3所示。桩端位移随时间、桩端位移随冲击速度、冲击力随时间、最大冲击力随冲击速度、砧座应力随时间、最大应力随冲击速度的变化曲线如图6至图11所示。

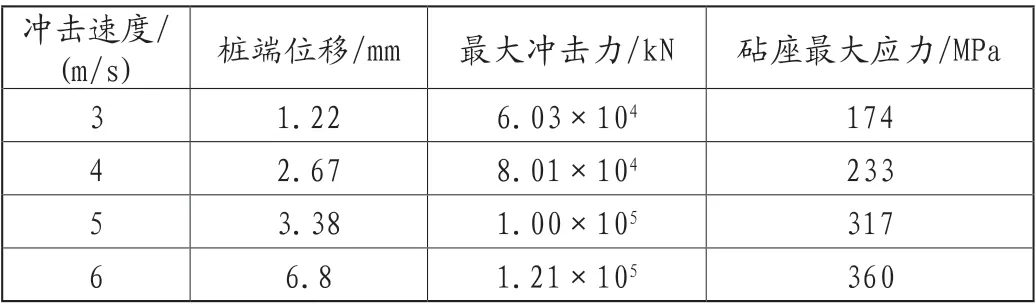
表3 不同冲击能量下桩端位移、最大冲击力和砧座最大应力

图6 桩端位移随时间变化曲线图

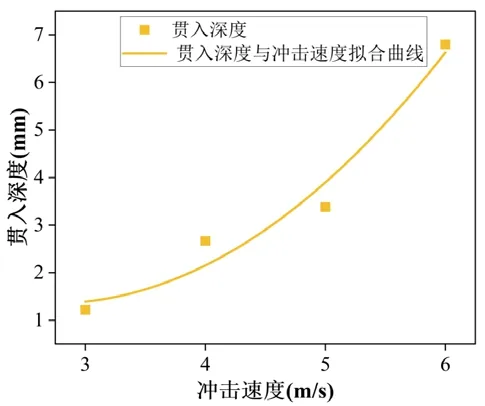
图7 桩端位移随冲击速度变化曲线图

由图6和图7可知，桩端位移先增大后减小，最终稳定，稳定后的位移是钢桩的实际贯入深度，冲击速度由3m/s增大到6m/s时，对应的贯入深度逐渐增加，表明贯入深度随冲击能量增加而增大。

由图8和图9可知，冲击力随着冲击速度的增大而增大，冲击力近似为一阶跃信号，冲击作用时间近似为5ms；冲击速度由3m/s增大到6m/s时，最大冲击力随冲击速度增加呈线性变化。

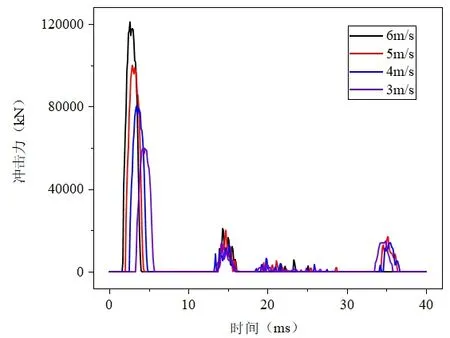
图8 冲击力随时间变化曲线图

图9 最大冲击力随冲击速度变化曲线图

由图10和图11可知，砧座应力随着冲击速度的增大而增大，且各个冲击速度下的最大应力值均符合强度设计要求；冲击速度由3m/s增大到6m/s时，砧座最大应力随冲击速度增加呈线性变化。

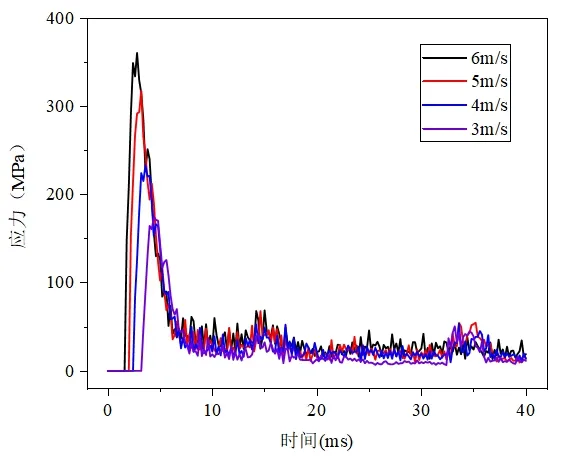
图10 砧座应力随时间变化曲线图

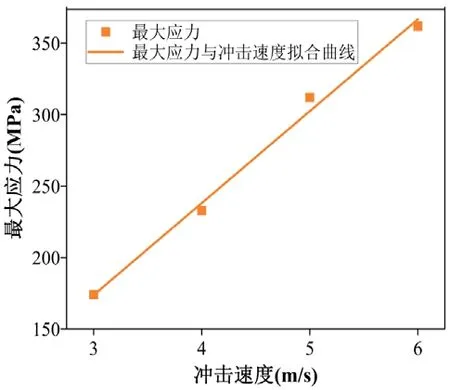
图11 砧座最大应力随冲击速度变化曲线图

5.结束语

（1）根据冲击能量在各部件中的传递情况，计算能量传递效率，得到冲击过程中各部件的应力分布，冲击力、应力以及钢桩的时程变化曲线。

（2）砧座最大应力达到360.361MPa，主要分在上接触面，且圆角处有应力集中现象；冲击系统的能量传递效率为91.86%。

（3）贯入深度、冲击力、冲击应力随着冲击能量的增大而增大，最大冲击力和最大冲击应力与速度呈线性变化关系。