自主行驶铲运机路径跟踪控制

朱 铭，吕 潇，张元生，李佳梦，刘 鹏，孙 昊

(1.矿冶科技集团有限公司，北京 100160； 2.北京北矿智能科技有限公司，北京 102628； 3.金属矿山智能开采技术北京市重点实验室，北京 102628； 4.矿冶过程自动控制技术国家重点实验室，北京 102628)

随着我国对矿产资源的逐步勘探与开采，浅部矿产资源已开发殆尽。我国作为矿藏资源丰富的国家，更多的矿产资源深埋在千米之下。当前我国近三分之一的矿山开采已达到1 000 m深度。深部采矿面临着许多挑战，如矿山建设难度大、开采作业困难、环境恶劣、安全风险较高等；井下青年从业人员越来越少，采矿领域人口老龄化现象严重[1]；疫情对密集型劳动产业影响较大，严重影响了矿山的生产效率。发展智能化、自动化的采矿装备，革新矿山开采模式，减少井下作业人员，提高生产流程的自动化与智能化，精确化管控生产计划，是我国资源开发尤其是深部资源开采的必然选择和必经之路[2]。

本文以Atlas Copco ST3.5铲运机为研究对象，展开了对铰接式车辆的运动学建模与自动驾驶控制策略的研究。推导适用于铰接车控制的基于偏差的线性模型预测控制器，并进行了仿真对比分析与实车验证。

1 模型预测控制

1.1 铲运机预测模型

当前针对铰接式车辆存在两种较为主流的建模方式，即基于运动学建模和依据动力学建模。在算法中使用车辆模型，计算的实时性是一个非常重要的算法评价指标，越复杂的车辆模型意味着要占用更多的计算资源和更长的求解时间，对于一个实时性要求较高的算法，过于复杂的模型研究并非重点，一定的简化和近似必不可少[3]。由于运动学模型具有简单的结构和尚可的模型精确度，故本文控制部分采用铰接车的运动学模型[4]。

忽略铰接式车辆在运动过程中的轮胎力学特性，可搭建如图1所示的运动学特征图[5]。

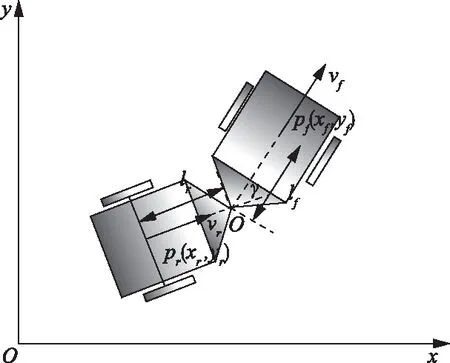
图1 铰接车运动学分析Fig.1 Kinematic analysis of articulated vehicle

当铰接式车辆行驶时，分析前车轴中心处的速度与前车身航向角关系。位姿状态Pf=[xf，yf，θf，γ]与前车身速度、铰接角速度写为如下状态空间方程[6]：

(1)

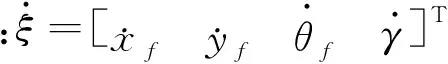
上述状态空间为非线性，采用近似线性化方法泰勒展开进行处理，得到：

(2)

式中，Jf(ξ)为f相对于ξ的雅克比矩阵，Jf(u)为f相对于u的雅克比矩阵。处理后可以得到：

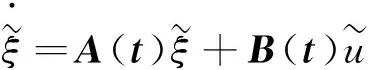
(3)

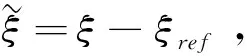
将得到的新状态方程采用前向欧拉法离散化处理后整理得到一个新的状态空间表达式：

(4)

(5)

设定控制系统的预测时域为NP，控制时域为NC，则预测时域内的状态量偏差和系统控制增量可以表示为：

(6)

(7)

将上式计算系统的预测输出简化为矩阵形式如下：

Y(t)=ψtξ(t|t)+ΘtΔU(t)

(8)

每一项矩阵如下：

通过上式可以求出控制器未来NP次循环的x向、y向、航向角、铰接角角度与预测的偏差和参考控制量的偏差。

1.2 优化求解

优化求解是模型预测控制中求解系统的控制增量部分，并将控制增量用于实际输出和预测模型。将控制增量作为目标函数的状态量，得到目标函数：

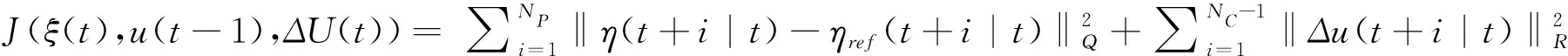
(9)

优化后的目标函数中第一项求和累加了预测时域内状态量与参考状态间的偏差，考虑到了未来的跟踪效果。第二项起到了调节控制量平稳性的作用。

控制量约束：

umin(t+k)≤u(t+k)≤umax(t+k)，k=0，1，…，NC-1

控制增量约束：

Δumin(t+k)≤Δu(t+k)≤Δumax(t+k)，k=0，1，…，NC-1

(10)

车辆状态约束为：

ymin(t+k)≤y(t+k)≤ymax(t+k)，k=0，1，…，NC-1

(11)

引入松弛因子，如下所示：

(12)

式中：ρ为权重系数；ε为松弛因子。

通过求解以上带约束的目标函数，可以得到一个控制序列，控制量个数为NC。

1.3 反馈控制

模型预测控制在每个控制周期根据环境反馈的车辆状态，更新状态空间方程内的矩阵参数，进行一轮预测控制求解可以得到LMPC对未来目标的控制序列，将控制序列的第一个控制量输出至系统。如式(13)所示：

u(t)=u(t-1)+Δu×t

(13)

系统接收到此控制指令后作出相应的动作，得到下一时刻环境反馈的状态量，输入至控制器，控制器重复之前动作，循环往复完成控制过程。此过程可以一定程度上避免由于系统干扰或是模型不精确导致的控制失败问题。

2 仿真试验

采用MapleSim搭建铲运机保真模型，如图2所示。根据铲运机外形尺寸，搭建车辆的左右转向液压缸及限位约束、前后车架、添加等效质心等。轮胎使用了“Tire Force and Moments”元件库中的“Fiala Tire SubSys”动力学模型。

图2 铲运机车辆模型Fig.2 LHD vehicle model

仿真平台选择MATLAB R2018a版本，将MapleSim车辆模型和模型预测控制器导入Simulink中，根据实车情况设置约束条件，搭建整车控制框架进行仿真。仿真框架如图3所示。

图3 仿真框架Fig.3 Simulation framework

跟踪效果与控制偏差如图4～7所示。

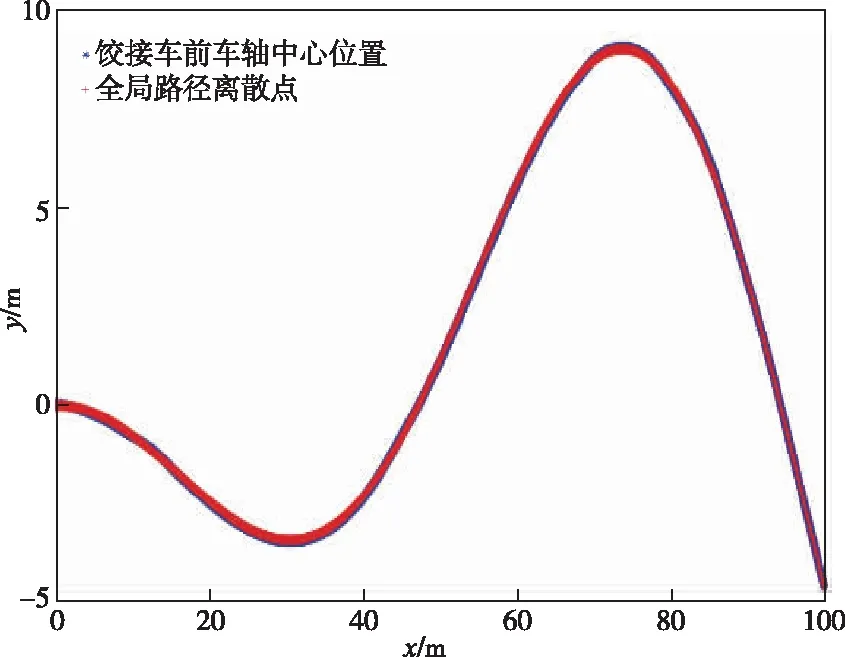
图4 跟踪控制效果Fig.4 Path following control performance

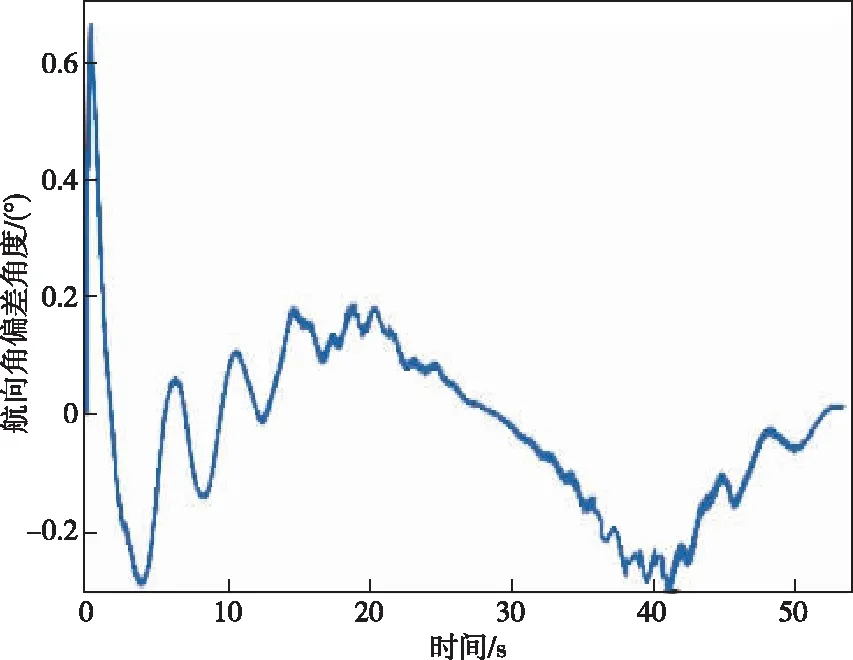
图6 航向角控制偏差Fig.6 Heading angle deviation

图7 铰接角控制偏差Fig.7 Articulation angle deviation

考虑到实际工业应用时采集数据与控制指令下发均为离散型数据，因此在仿真中模拟这一特点使用离散的参考路径点。本文采用兼顾左右转向、变曲率的全局路径，将其进行离散插值得到一系列离散点，之后以车辆根据当前位置寻找最近参考路径点进行迭代运算。

从轨迹上观察四状态偏差的LMPC控制策略可以较准确地跟踪参考路径，车辆行驶的路径未出现明显的偏差。根据当前车辆所处位置自动寻找该全局路径上最近的参考点进行跟踪，这样得到的参考点能较好地匹配当前车辆的位置信息，并且避免了由于模型误差推算导致的误差累计问题。全程中本文提出的四状态偏差LMPC控制策略在y向的最大偏差约为0.06 m，行驶中航向角偏差不超过0.3°，跟踪全过程中最大铰接角控制偏差小于0.8°。在变曲率的路径下依然具有不错的控制精度。

3 实车试验

于三山岛金矿-645中段开展井下自动驾驶试验，选用车型为Atlas Copco ST3.5铲运机(见图8)。

图8 ST3.5铲运机在-645中段Fig.8 ST3.5 scraper at -645 middle section

-645中段为矿上生产中段，矿车需从主斜坡道下至该中段，将矿车运载的矿石物料运至溜井口破碎(见图9)。该中段巷道俯视图如图10所示。图中起点处即为该中段入口，终点为溜井口位置。

图9 铲运机在巷道中自动行驶Fig.9 Scraper auto driving in underground roadway

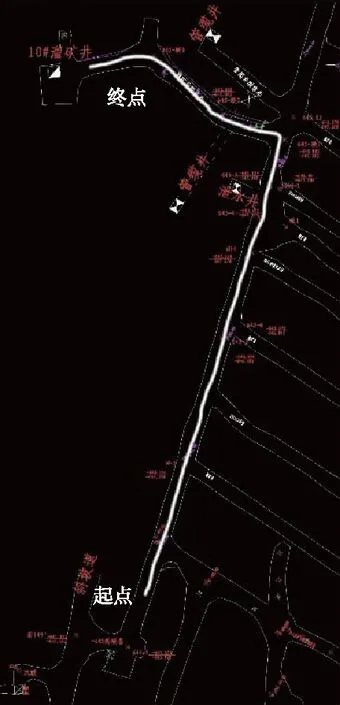
图10 -645中段作业路线Fig.10 -645 middle section operation route

采用多线激光雷达SLAM定位得到车辆在全局地图的坐标，预设不同路径得到自动驾驶跟踪效果如图11所示。

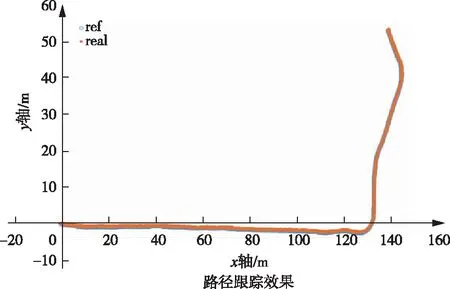
图11 ST3.5铲运机路径跟踪效果Fig.11 Path following control performance of ST 3.5 scraper

图11中蓝色ref代表预设路径，红色real为铲运机实际跟踪轨迹，自动驾驶铲运机可较好地跟随全局预设路径，完成运输任务。各状态偏差控制效果如图12～17所示。

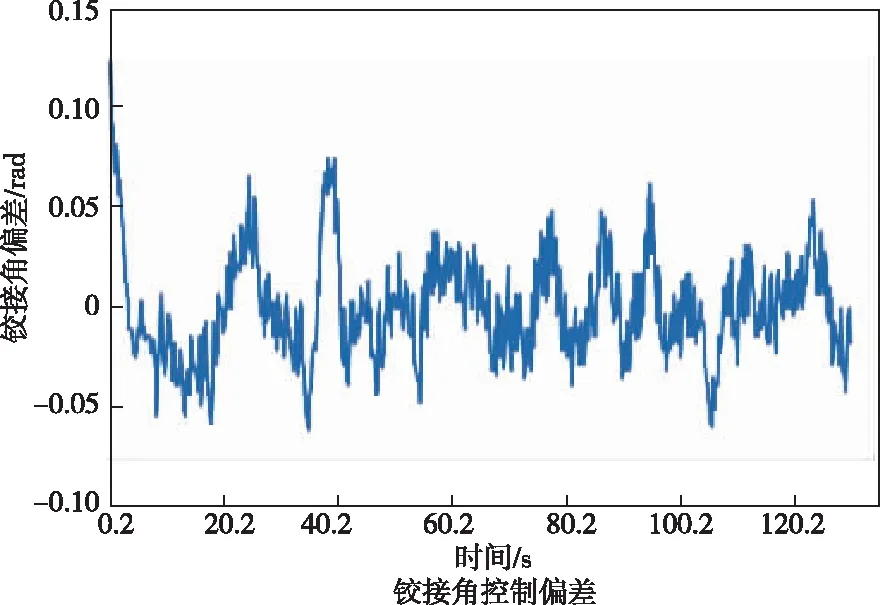
图12 ST3.5铲运机铰接角控制偏差Fig.12 Articulation angle deviation of ST 3.5 scraper

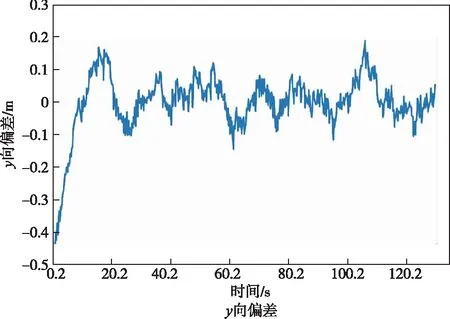
图13 ST3.5铲运机y向控制偏差Fig.13 Y-direction deviation of ST 3.5 scraper

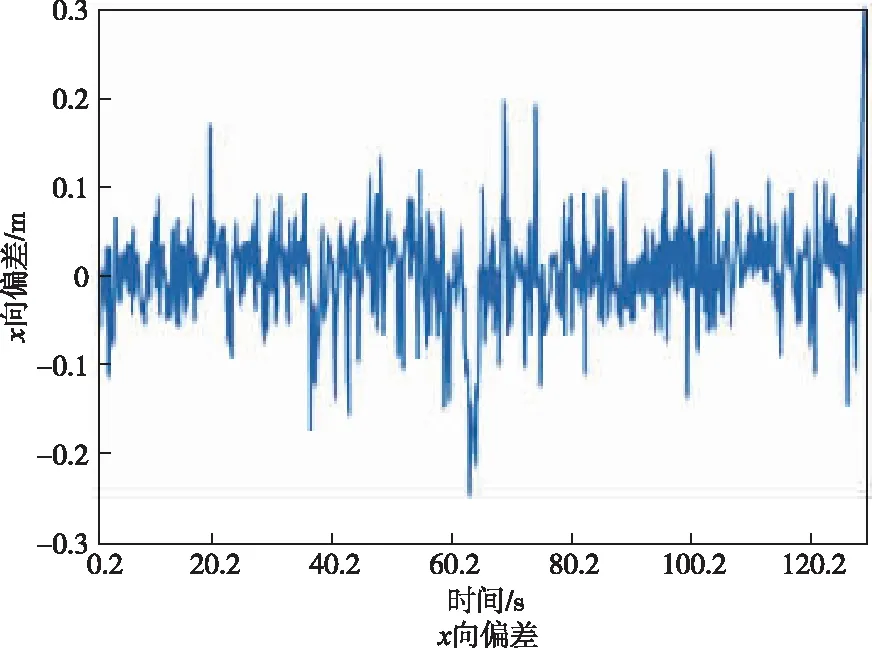
图14 ST3.5铲运机x向控制偏差Fig.14 X-direction deviation of ST 3.5 scraper

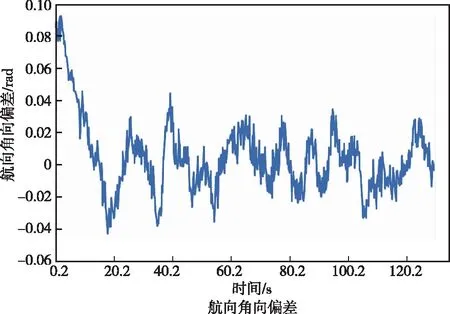
图15 ST3.5铲运机航向角控制偏差Fig.15 Heading angle deviation of ST 3.5 scraper

图16 ST3.5铲运机航向角控制效果Fig.16 Heading angle control performance of ST 3.5 scraper

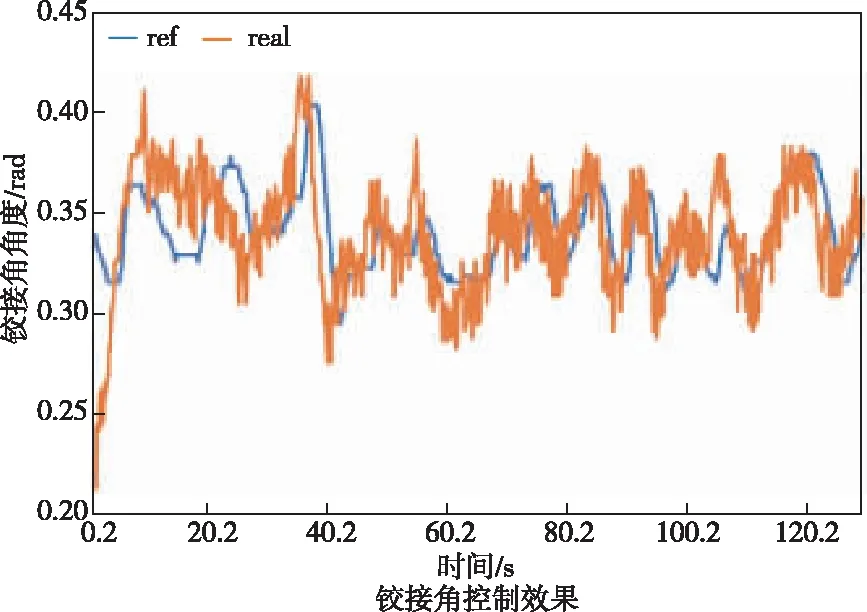
图17 ST3.5铲运机铰接角控制效果Fig.17 Articulation angle control performance of ST 3.5 scraper

除去起步时初始偏差外，行驶途中y向偏差正向保持在0.2 m以内，负向偏差小于0.15 m，x向偏差绝对值小于0.3 m，整体较好地跟踪了预设路径内最近点的坐标位置。同时航向角控制偏差与铰接角控制偏差也分别保持在0.042 rad(约2.4°)与0.075 rad(约4.3°)以内，控制误差均保持在合理的范围内。

4 结论

本文提出的四状态偏差MPC控制算法，经仿真验证y向最大偏差约为0.06 m，行驶中航向角偏差不超过0.3°，跟踪全过程中最大铰接角控制偏差小于0.8°。实车试验中y向最大偏差约为0.2 m，x向最大偏差约为0.3 m，行驶中航向角偏差不超过0.042 rad(约2.4°)，最大铰接角控制偏差小于0.075 rad(约4.3°)，在约90°转向的弯道依旧保持良好的跟踪效果，经现场试验达到了实际铲运机自主行驶作业的路径跟踪精度要求，证明了本文提出的模型预测控制算法具有较好的实际应用效果，具备工业应用推广价值。