基于箱体振型特征的油浸式电抗器绕组松动识别方法
2023-02-22孟令明高树国丘子诚
孟令明,高树国,丘子诚,张 凡,欧 强,赵 军,张 宁
(1.国网河北省电力有限公司电力科学研究院,河北 石家庄 050021;2.西安交通大学电力设备电气绝缘国家重点实验室,陕西 西安 710049;3.特变电工衡阳变压器有限公司,湖南 衡阳 421007;4.国网河北省电力有限公司检修分公司,河北 石家庄 050021)
1 引言
高压并联电抗器作为电力系统中的关键设备,起着补偿线路上无功功率、抑制线路过电压的作用[1,2]。在长期运行的过程中,电抗器的振动很可能会造成电抗器内部紧固件以及铁心绕组等关键部件的松动,极端情况下可引起设备发生严重故障[3-5]。因此,及时评估电抗器关键部件松动状况,有效避免设备故障程度发生劣化,对电抗器的安全运行意义重大。
目前国内外学者针对电抗器振动特性进行了大量研究。关于电抗器的振动机理,目前的研究主要集中于仿真和实验。葛德馨通过仿真对电抗器的铁心、铁轭以及其他结构件进行了受力分析,在此基础上,对电抗器进行了整体的瞬态振动响应分析[6]。谭黎军等人对现场三台特高压并联电抗器进行了噪声与振动的测量实验,分析了振动以及噪声的频谱特性[7]。郭佳熠等人考虑到了气隙结构对电抗器振动的影响,通过搭建包含不同气隙个数及气隙在不同位置情况下的电抗器仿真模型,利用多物理场有限元仿真计算方法,得到了气隙结构对电抗器铁心振动的影响规律[8]。在故障诊断方面,国内学者利用信息多元化的信号分析方法,对电抗器运行状态进行分析:吴金利等人通过提取高压并联电抗器振动信号中的主成分系数等参数作为特征值,综合K-临近算法、支持向量、神经网络等多种机器学习方法实现对高压并联电抗器机械故障的诊断[9]。赵若妤等人提出了一种基于经验小波变换(Empirical Wavelet Transform,EWT)、多尺度数学形态谱进行特征提取,采用KernelK-means聚类进行故障模式识别的诊断新方法,并成功识别了几种工况下电抗器振动信号特征参数[10]。以上学者的研究从振动机理方面为振动法提供了理论基础,并通过实验得到了一些值得参考的故障诊断方法。
本文利用若干传感器测量一台500 kV电抗器油箱表面的振动信号,并通过运行变形振型(Operating Deflection Shapes,ODS)对其箱壁振动分布进行了可视化展示,通过升压实验分析电抗器表面振动幅值与电压之间的关系。应用灰度共生矩阵的图像纹理分析方法,对电抗器在正常状态下以及绕组松动状态下的两组不同振动分布进行了分析,并对比了图像特征值机械状态之间的对应关系,进而实现了电抗器绕组松动状态的检测。
2 高压并联电抗器振动机理
2.1 高压并联电抗器结构
并联电抗器主要由铁心和线圈等主要结构件组成,其绕组采用饼式结构。铁心是电抗器的核心,由铁心柱和铁轭组成;其铁心柱由若干个铁心饼叠加而成,铁心饼之间用绝缘垫块隔开,形成间隙,其铁轭结构与变压器相似;铁心柱与铁轭由压紧装置通过拉螺杆提供预紧力,形成一个整体。单相并联电抗器铁心为单心柱、两旁柱结构,铁轭宽度大于铁心柱直径,用以吸收部分漏磁[11]。图1为单相并联电抗器结构模型。
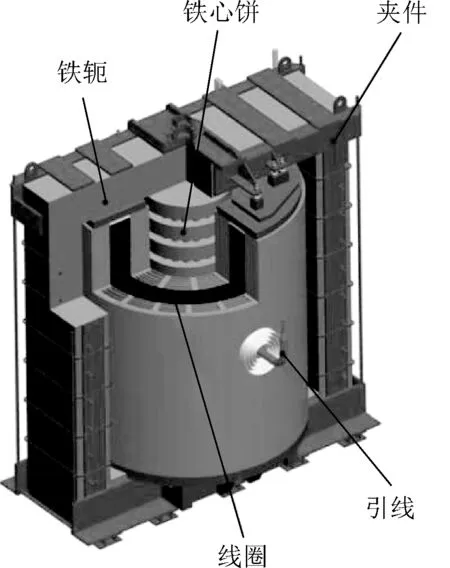
图1 高压并联电抗器结构Fig.1 Structure of high voltage shunt reactor
2.2 高压并联电抗器振动模型分析
高压并联电抗器的振动主要由绕组上的电磁力、硅钢片上的磁致伸缩效应和铁心饼间的麦克斯韦力引起。
造成高压并联电抗器中铁心产生振动的原因有两个:①由于铁心柱是分段的,在交变的电磁场作用下,铁心饼之间会产生麦克斯韦力,而麦克斯韦力会使磁场能量向变小的方向发展,从而造成铁心弹性形变;②由于铁心硅钢片的磁致伸缩效应会使得高压并联电抗器铁心产生周期性的伸长或收缩,进而产生振动。
绕组振动的产生是由于在高压并联电抗器稳定运行的过程中,其绕组线圈中流过电流时,由于漏磁场的存在,绕组间、线匝间产生动态电磁力,从而引起绕组的振动[12]。
对于铁心柱和绕组,两者都是由饼状结构堆叠而成。将高压并联电抗器铁心绕组的饼式结构简化为质量-弹簧数学模型,如图2所示[13]。在该数学模型中,上下压板被认为是刚体,其位置固定,不发生位移;每层线饼可等效为质量模块;而线饼间的绝缘垫块则可认为是为弹性元件。图2中,mi为第i层线饼质量;Fi为第i层线饼所受电磁力;Xi为第i层线饼位移;Ki为弹性系数;Ci为阻尼系数。通过该模型建立并求解运动微分方程组的方式来对绕组的位移、速度以及加速度进行计算分析。
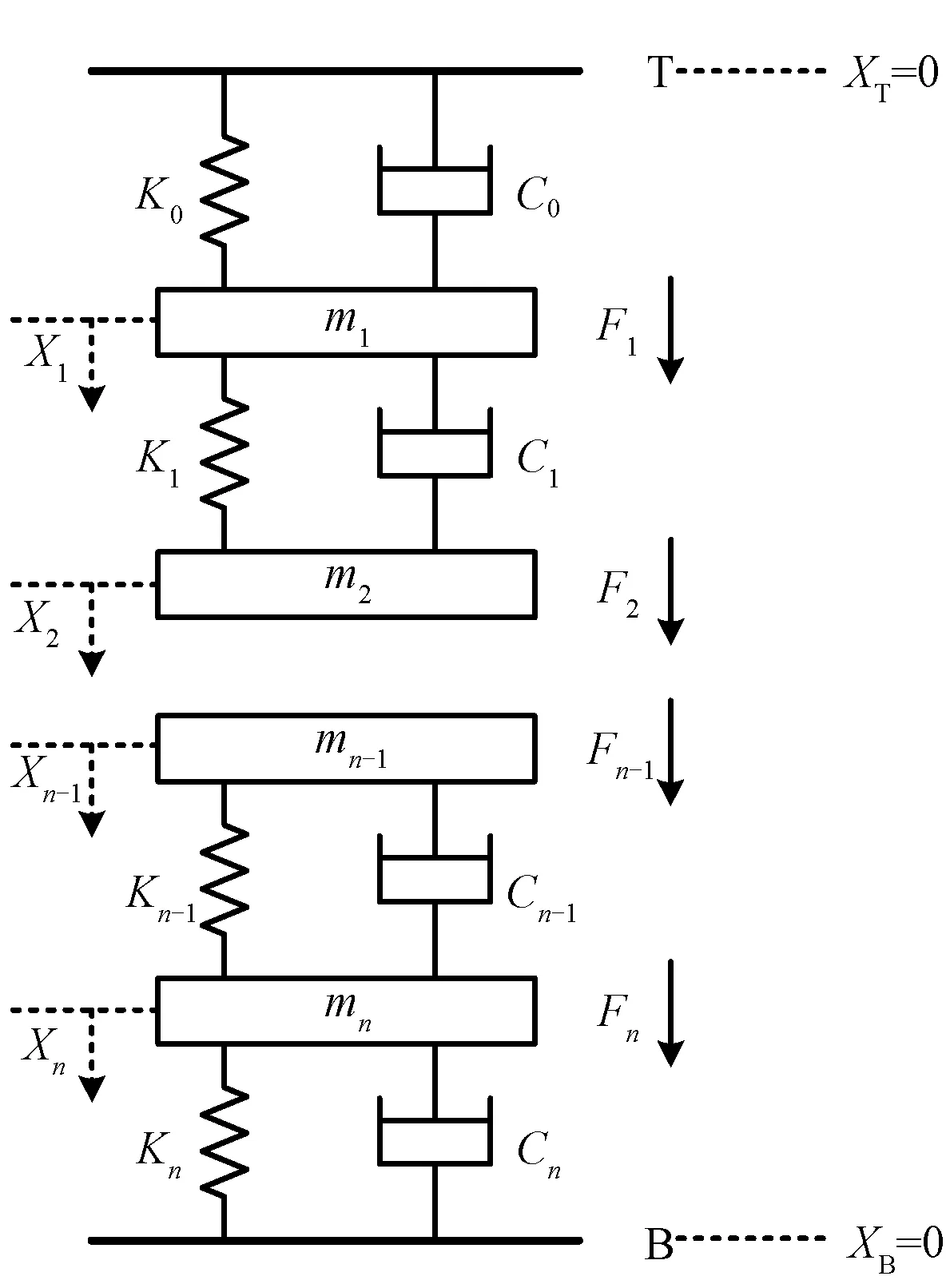
图2 饼式结构的轴向结构质量-弹簧数学模型Fig.2 Axial structure mass-spring mathematical model of cake structure
根据机械振动理论可得:
(1)
式中,Mw、C、Kw和xw分别为绕组的质量矩阵、阻尼矩阵、刚度矩阵和位移向量;Fw、Gw和t分别为电磁力矩阵、重力矩阵和时间。对于铁心柱,其表达式与式(1)类似,但实际操作条件受到麦克斯韦力与磁致伸缩效应的影响。
对于绕组振动,若忽略弹性系数以及阻尼系数C的非线性,式(1)可简化为具有常系数的非齐次二阶微分方程,求解该微分方程组,可得到简化的绕组振动加速度为:
(2)
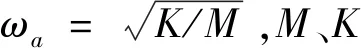
对于绕组振动,若忽略弹性系数K以及阻尼系数C的非线性,式(2)可简化为具有常系数的非齐次二阶微分方程,求解该微分方程组,可得到简化的绕组振动加速度。因此,实际稳态运行的电抗器振动信号中仅包含稳态分量,即并联电抗器绕组振动信号的频率是电源频率的2倍。实际情况中,由于绕组绝缘垫块材料的非线性特性,绕组的振动信号中也可能存在100 Hz的倍频谐波[14]。
3 ODS成像原理及图像分析方法
3.1 ODS成像原理
本文以一台500 kV单相电抗器为研究对象,测量所用到的传感器由14通道的振动加速度传感器以及1通道的电流信号传感器组成,整体实验平台如图3、图4所示。

图3 实验电抗器Fig.3 Test reactor
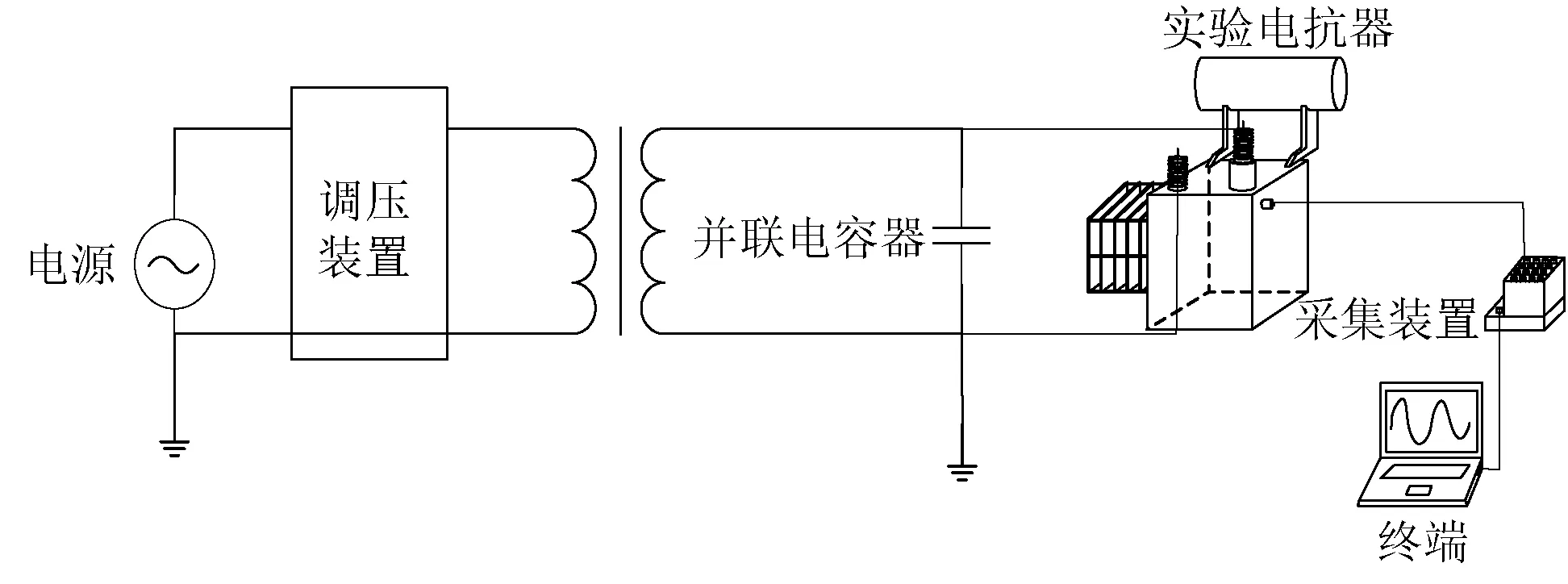
图4 实验平台Fig.4 Test platform
理论上,生成ODS图像需要同时测量电抗器表面上的所有测点,但在箱体表面布置过多的传感器并不切合实际,同时过多的传感器在一定程度上会改变箱体模态,从而影响测量结果。因此选择对箱体同一表面进行分批次测量,由于每批次测量的时刻不同,导致针对各测点获取到的振动信号可能存在初相角偏移,因此需要对每批次的振动信号进行相位校正[15]。
相位校正就是在每次测量的同时引入一个参考点的测量。由于参考点和测量点同时测量,因此它们的相位差是固定的。而两次不同的测量之间,参考点之间的相位差也是固定的,由此便可以实现相位校正。本文选取电流信号作为参考点信号,这是因为电流信号只存在50 Hz,不存在其余谐波,且不容易受到电抗器工况以及周围环境的干扰。
在进行了相位校正过后,对各测点所得信号进行频域分析,得到频域ODS,如下所示:
fODS(φ)=diag(φ)X(φ)
(3)
式中,diag(φ)为测点信号与基准信号相位差对角矩阵;X(φ)为各测点信号幅值频谱向量[16]。
3.2 灰度共生矩阵分析方法
图像的纹理分析指通过一定的图像处理技术提取纹理特征参数,由于ODS可直观地反映电抗器运行期间其箱体表面在某一特定频率下的振动形态,因此当绕组的松动状态发生改变时,电抗器本体振动形态改变,因此传播至油箱表面的振动信号特征也发生波动,ODS图像也随之改变。运用图像纹理分析技术可以从中提取到特征值,进一步判断绕组松动状态。图像纹理分析技术现已生成很多算法,灰度共生矩阵是其中重要的一种,在分类精度提高研究方面具有有效性[16]。电抗器的ODS图像灰度信息丰富,对机械状态变化的反应更为灵敏。因此本文使用灰度共生矩阵来提取ODS图像中的纹理特征。
灰度共生矩阵又称灰度级空间依赖性矩阵,它是在假定图像中各像素间的空间分布关系包含了图像纹理信息的前提下,提出具有广泛性的纹理分析方法。灰度共生矩阵通过统计各种灰度级对在不同方向上出现的概率来生成灰度共生矩阵,再通过算法提取特征值,进而表示不同方向上的纹理特征。
如图5所示,灰度共生矩阵的具体生成过程如下:
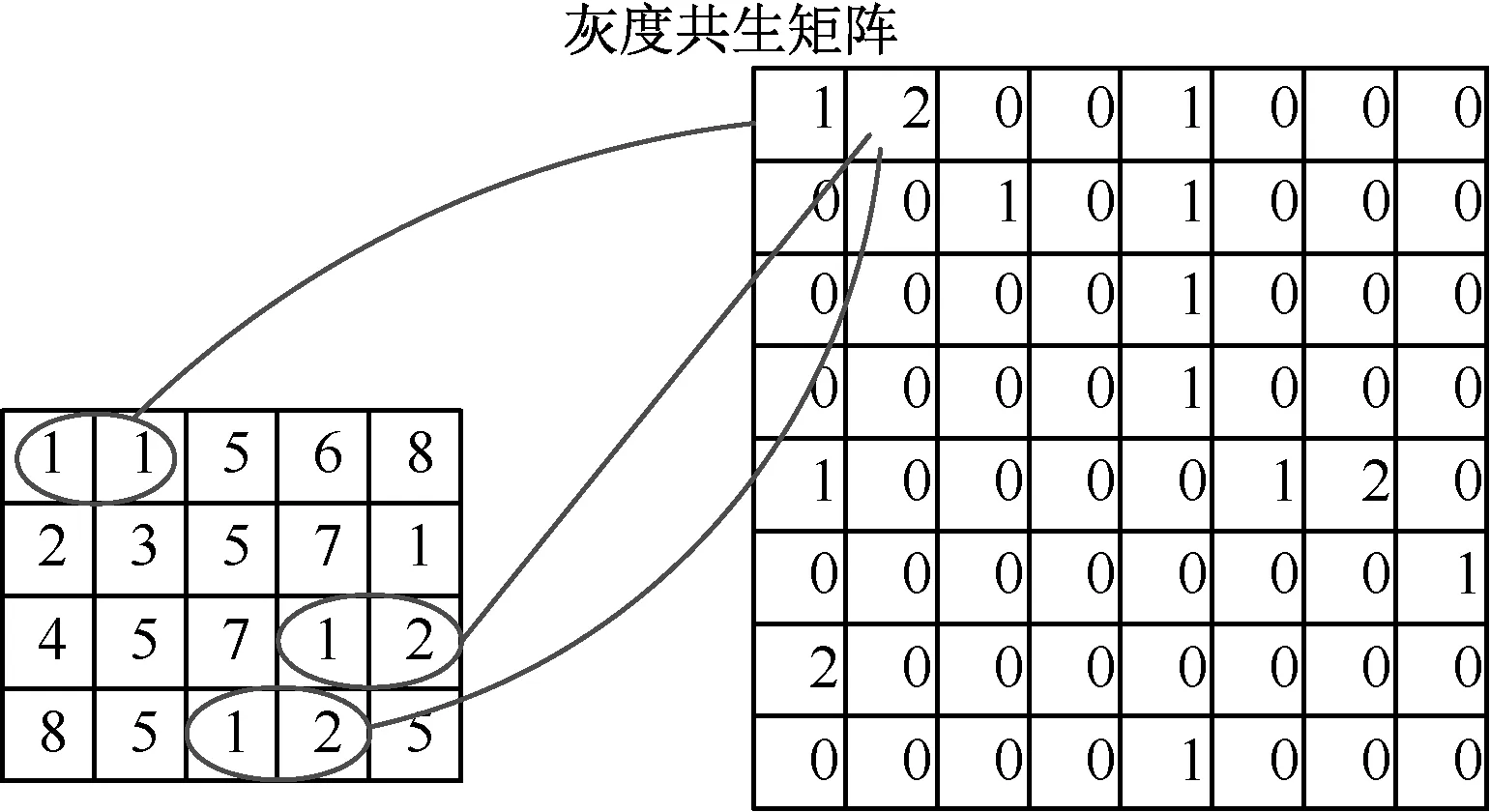
图5 灰度共生矩阵生成Fig.5 Generation of gray level co-occurrence matrix
以水平方向为例,灰度图的灰度等级为8,由相邻灰度级为(1,1)的灰度级开始,一直遍历到(8,8),最后生成一个8×8的矩阵,即灰度共生矩阵。本文中将取0°、45°、90°、135°四个方向的角度分别求取灰度共生矩阵,这样可以更好地反映图像各个方向上的纹理特征。基于灰度共生矩阵的特征量有很多,本文采取能量、相关性和同质性来反映图像的纹理特征[17,18]。
能量(Asm)反映了图像的灰度变化均匀程度,如果能量较小,则说明灰度共生矩阵元素值较为接近,表示纹理变化较为均匀。反之,则说明纹理变化较为剧烈。其计算公式为:
(4)
式中,G(i,j)为灰度对出现的概率。
相关性(Correlation,Cor)表征像素对组出现的联合概率,即灰度共生矩阵的值在行与行或列与列方向上的相似程度,行或列之间矩阵值变化大时,相关性小,反之相关性大。其计算公式为:
(5)
式中,μ为均值;σi、σj为标准差。
逆差距(Inverse Difference Moment,IDM)表征灰度图像纹理局部变化的多少。若图像的不同区域间缺少变化,则IDM大;反之,如果图像的不同区域间变化很大,则IDM小[19]。计算如下:
(6)
式中,|i-j|为像素对的灰度差[20]。
4 振动实验过程及分析
4.1 振动实验流程
由于电抗器箱体表面并不平整,其表面可能存在电抗器外表面结构件以及加强筋等部件,对每个区域准确均匀地获取信号形成障碍,因此选取套管面及其相对的另一侧面作为测量面。为了便于区分文中信号来源,定义高压套管侧为电抗器油箱正面,与高压套管相对的另一侧为油箱背面,两个平面的测点分布如图6所示。
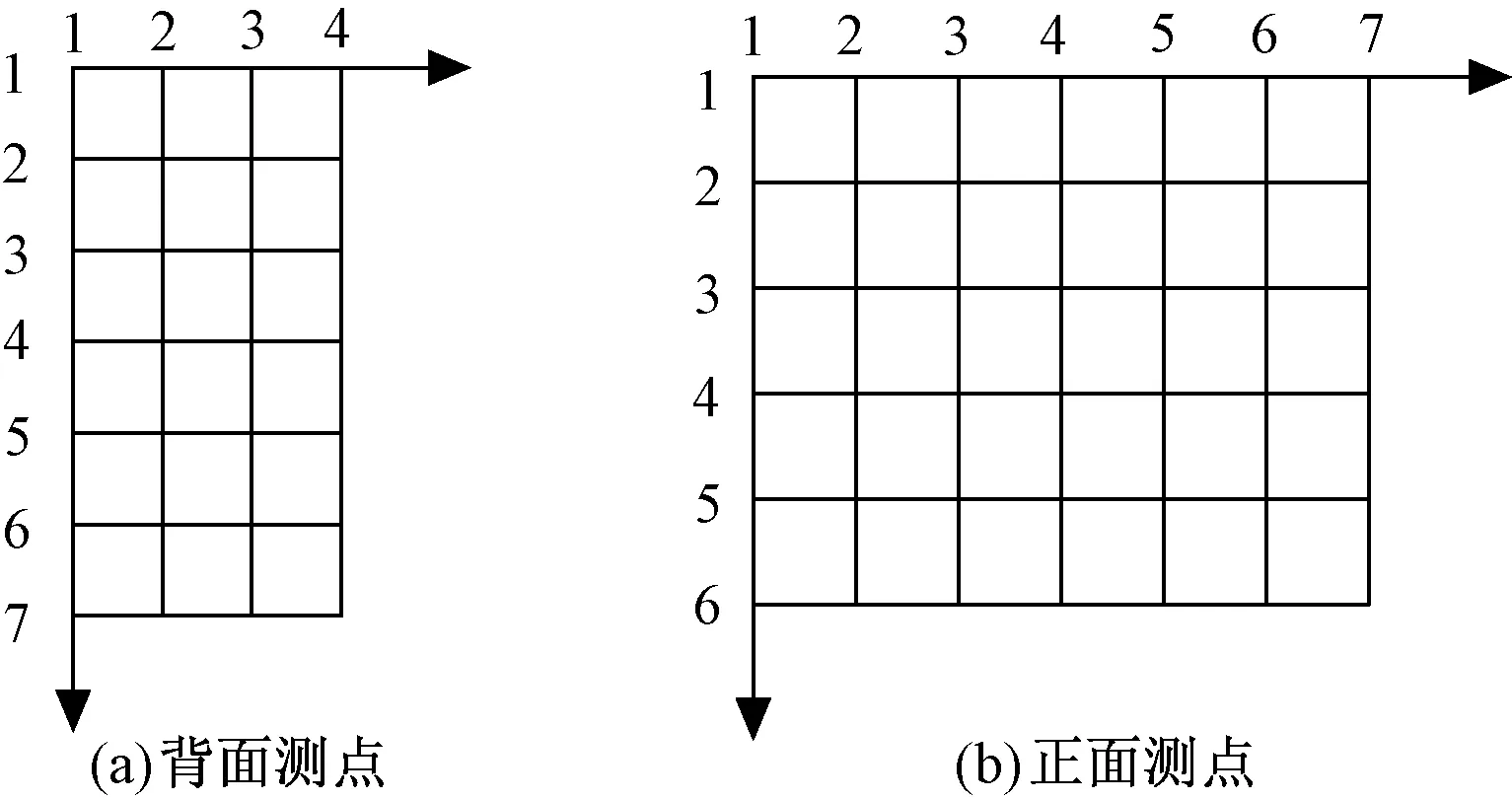
图6 电抗器表面测点分布Fig.6 Points on surface of reactor
为了保证箱体振动分布的一致性,测量区域内的测点位置采用均匀分布,电抗器正面布置7×6个测点,背面布置4×7个测点。
在电抗器实验过程中,调整绕组轴向压紧力以模拟绕组松动状态,与电抗器正常状态下的振动信号形成对比。
同时,对不同机械状态下的电抗器进行升压实验,以获取振动幅值与振动分布随电压升高的变化趋势。升压实验过程中,选取了50%、75%、100%额定电压作为电抗器三种不同运行工况。
4.2 升压实验及ODS图像分析
在升压实验中,选取了50%、75%、100%额定电压三种电压等级,并提取基频振动加速度。电抗器表面基频振动加速度和归一化电压平方之间的关系如图7和图8所示。
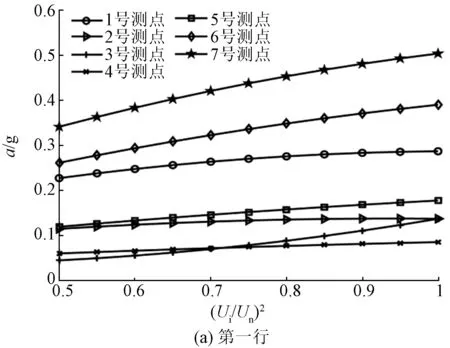
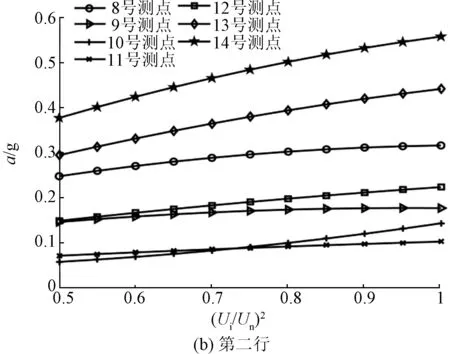
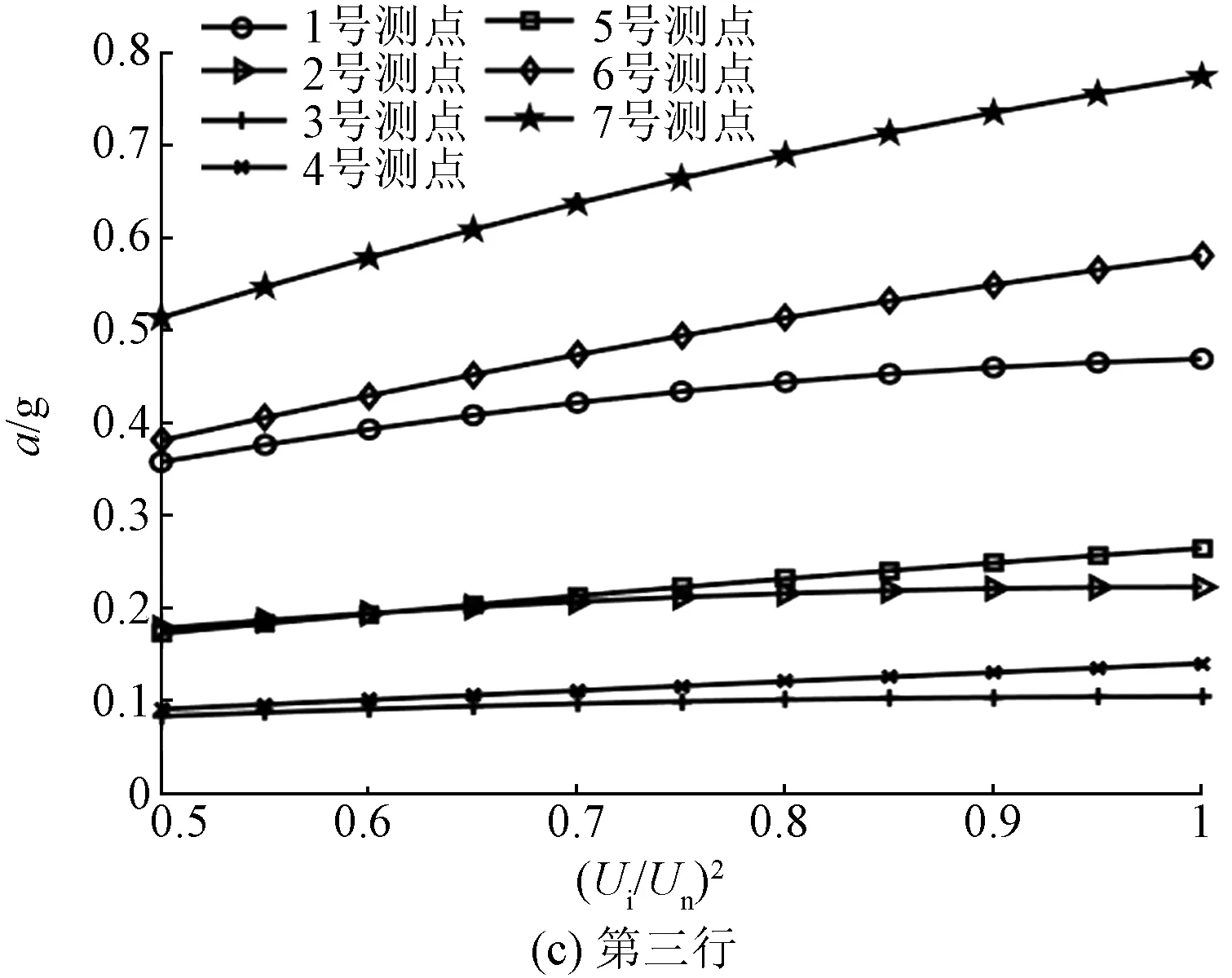
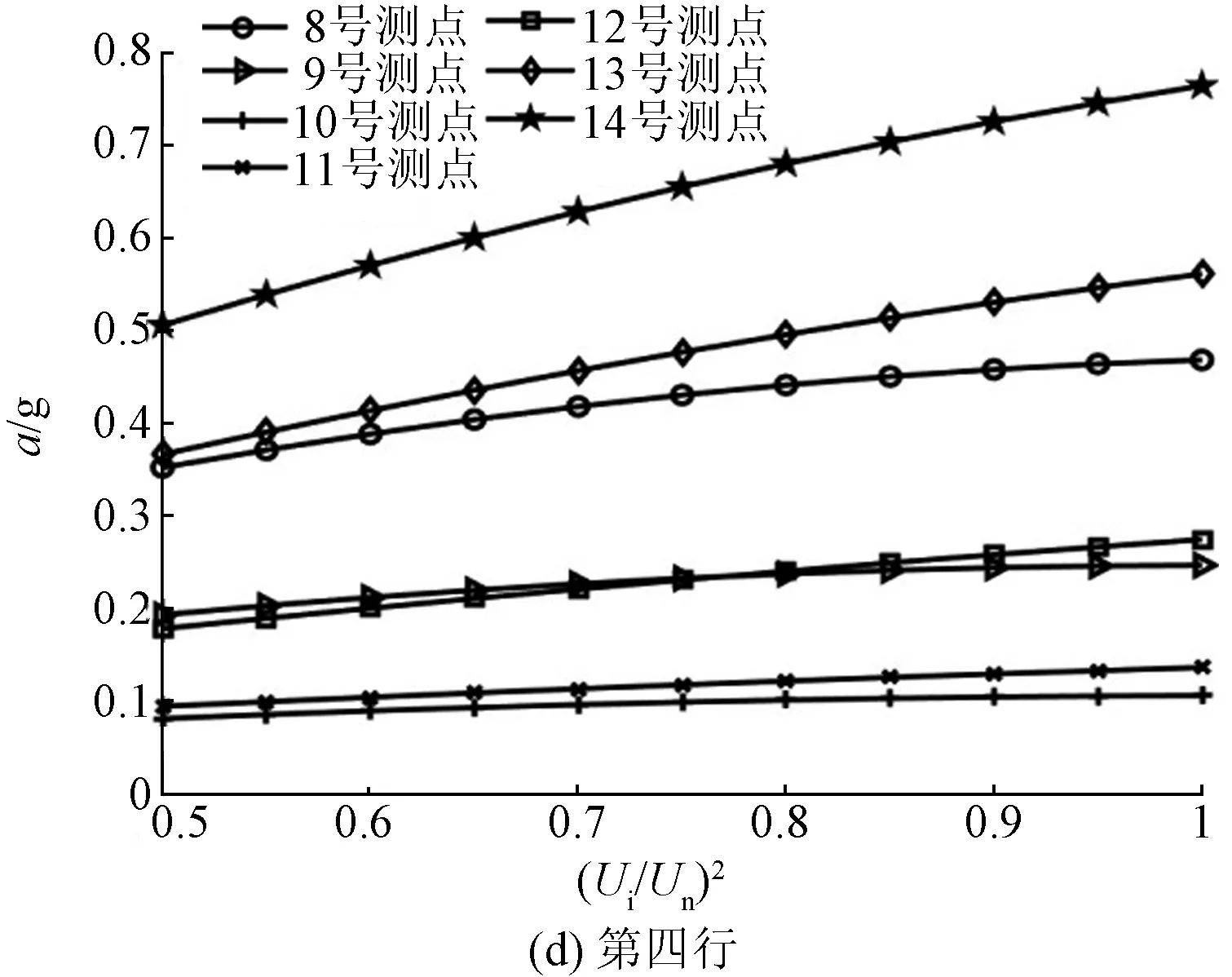
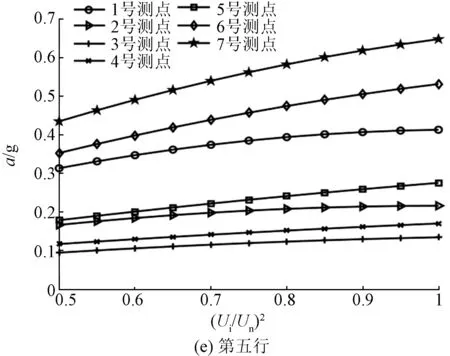
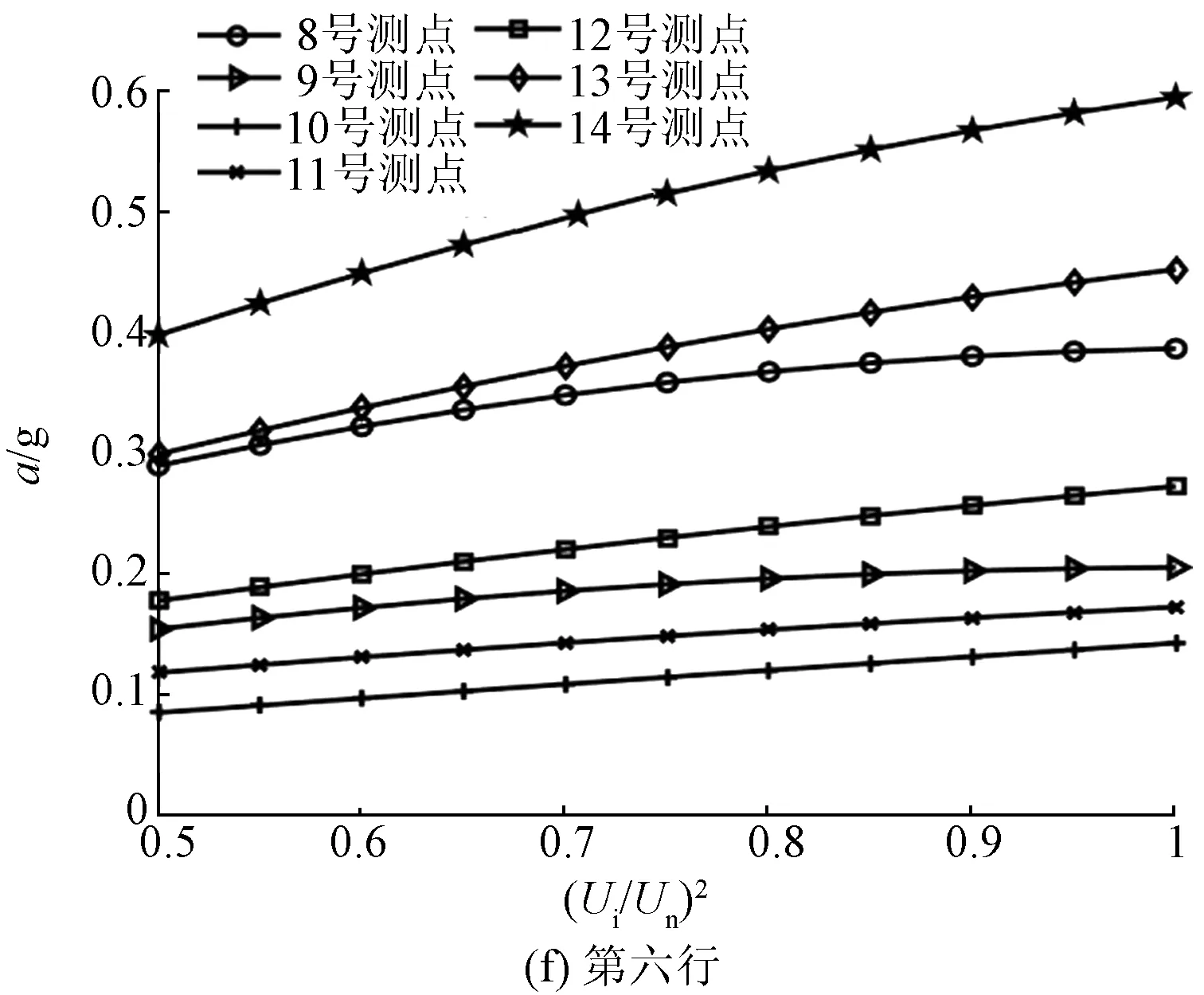
图7 电抗器正面表面振动加速度与电压平方之间的关系Fig.7 Relationship between vibration acceleration and square of voltage of reactor front side
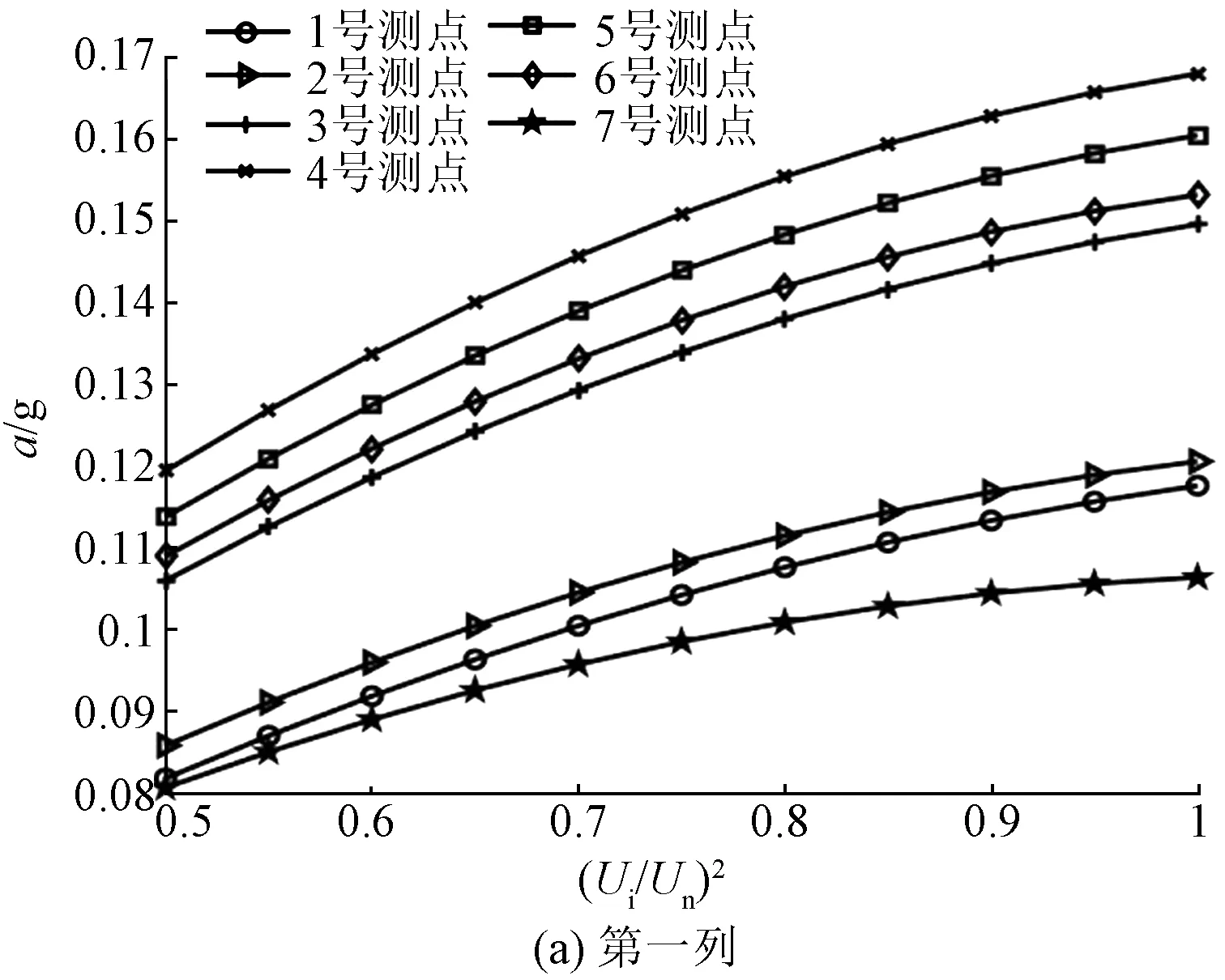
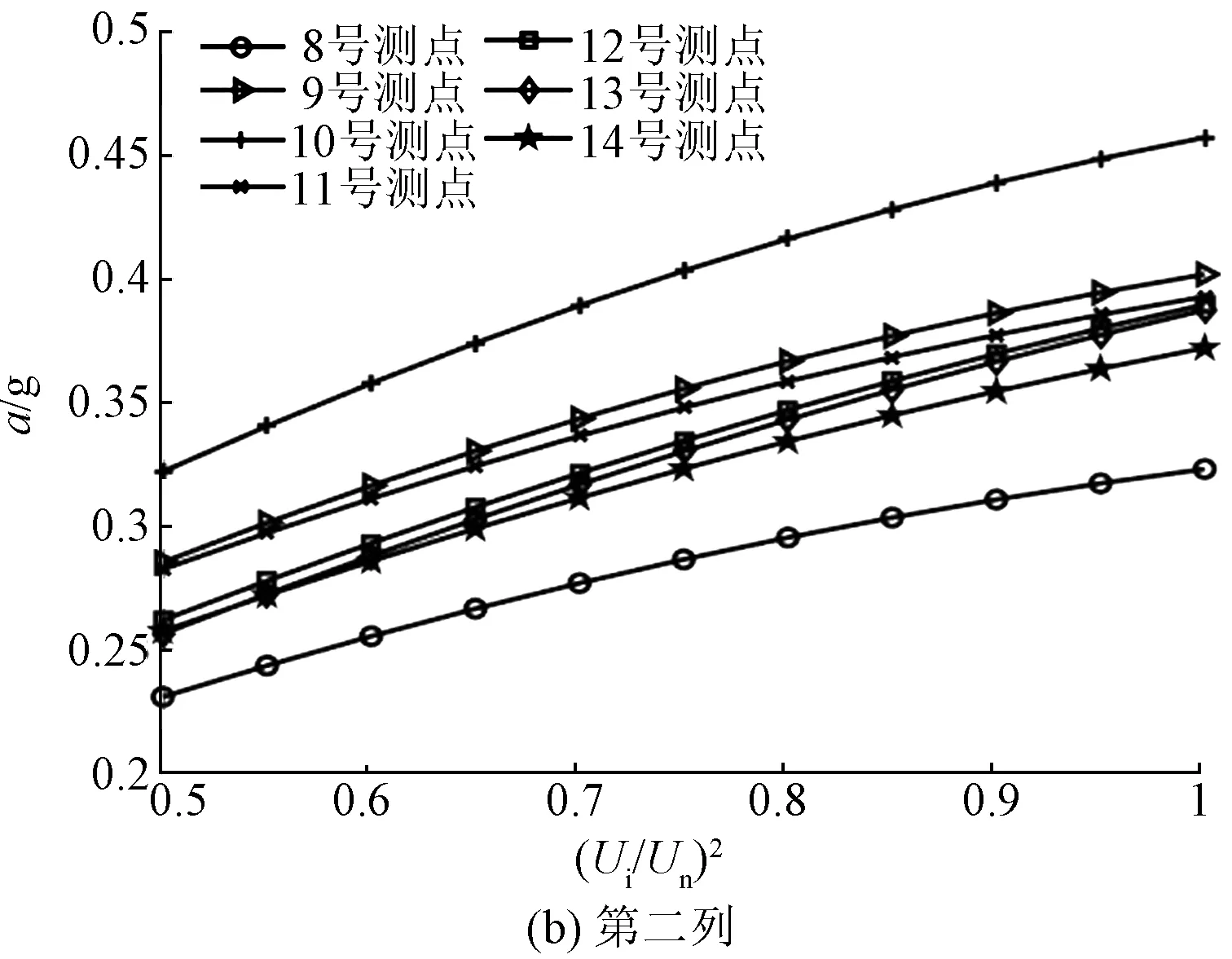
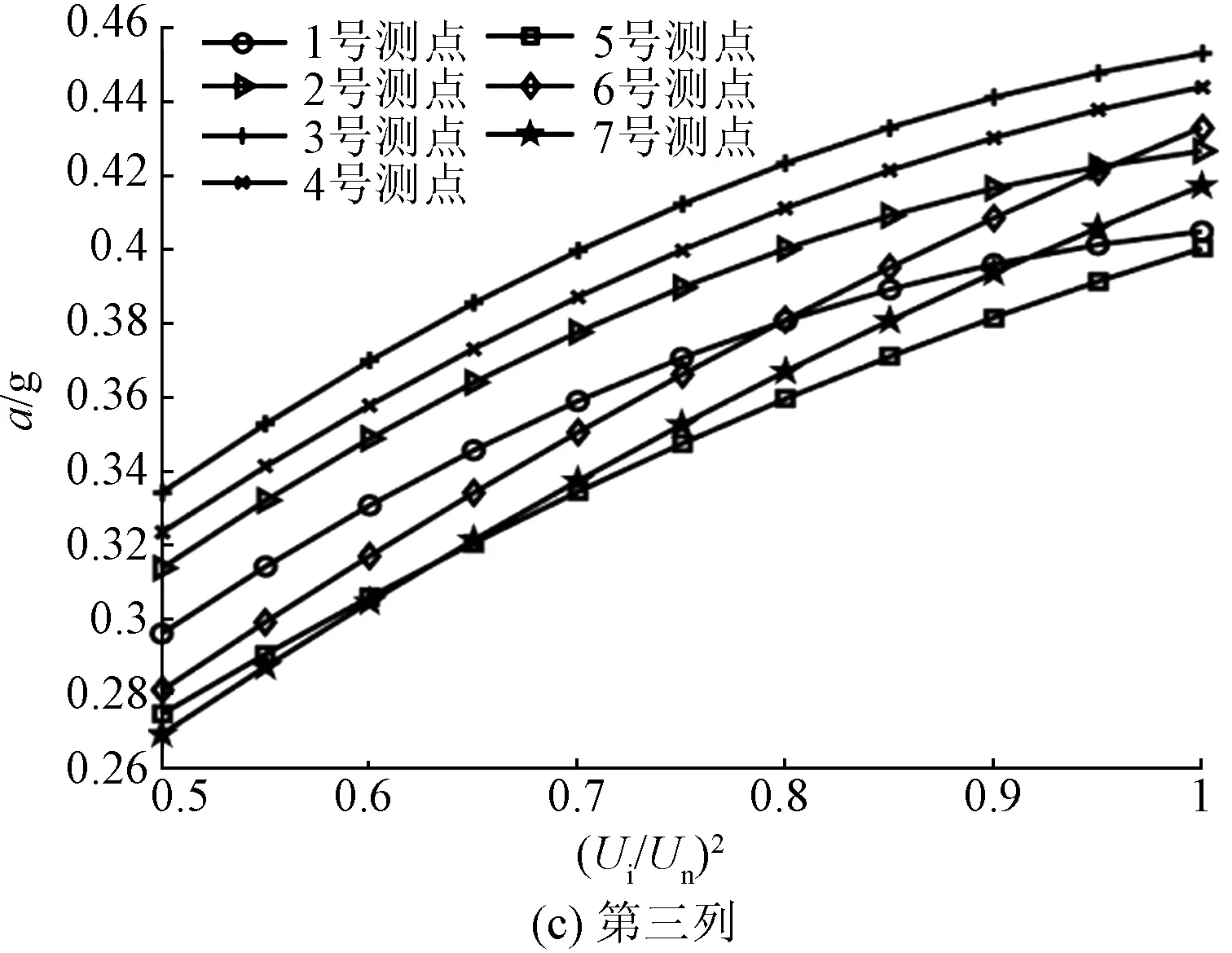
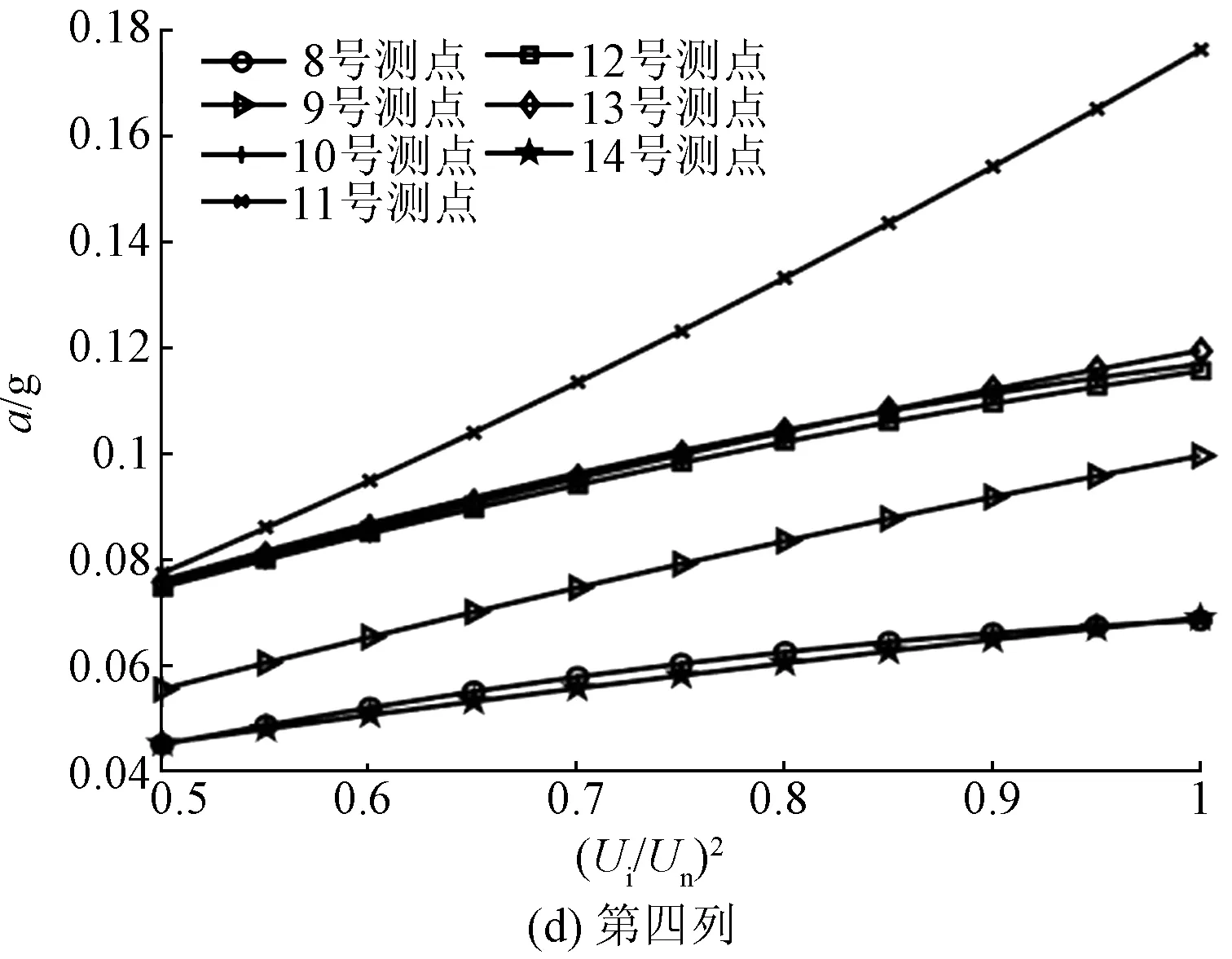
图8 电抗器背面表面振动加速度与电压平方之间的关系Fig.8 Relationship between vibration acceleration and square of voltage of reactor back side
如图8所示,电抗器背面表面加速度和归一化电压平方成正比关系。为了充分说明振动加速度幅值与归一化电压平方之间的线性度关系,利用多项式曲线拟合对不同电压等级下的振动加速度幅值做线性拟合,并引入回归分析中的R-square评价振动幅值与归一化电压平方的线性度:
(7)
(8)
(9)
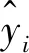
表1、表2为电抗器油箱表面各测点振动加速度幅值与归一化电压平方经拟合后R-square的大小。
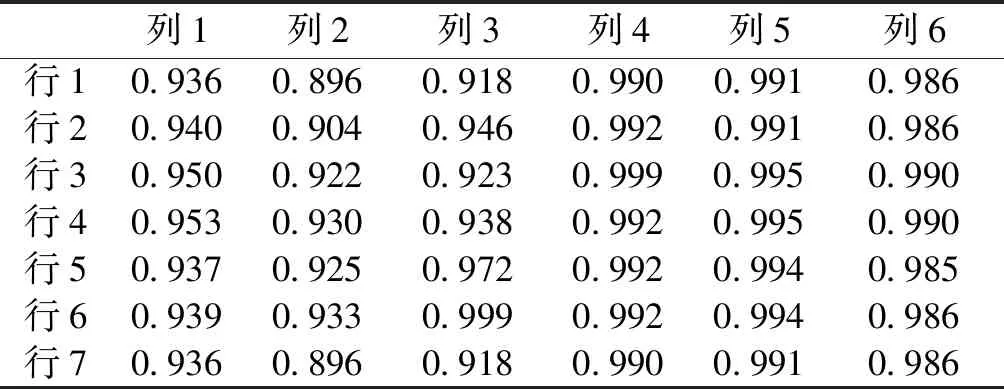
表1 电抗器正面表面不同测点R-square大小Tab.1 R-square on surface of front side of shunt reactor
表2 电抗器背面表面不同测点R-square大小Tab.2 R-square on surface of back side of shunt reactor
由表1、表2可知,绝大多数测点的R-square大小均大于0.9,这说明了测点振动加速度与归一化电压平方之间的线性度良好,对于正面测点(3,4)与(6,3)、背面测点(2,4)与(7,4),其R-square值大于0.99,该测点的振动加速度与归一化电压平方线性度更高。而对于正面测点(1,2)与背面测点(7,1),其R-square相对较小,其原因可能是由于个别测点不可避免地受到套管或内部紧固件的影响,在电抗器内部振动的传递过程中,这些部件自身的受迫振动对于电抗器铁心绕组的振动产生了一定的干扰,从而导致位于该位置测点的振动加速度和归一化电压平方之间的线性度不高。
电抗器表面振动加速度和归一化电压之间的关系同样可以由ODS图像表示,电抗器表面100 Hz频率在不同电压下的ODS图像如图9所示。由图9可知,ODS图像分布随电压升高并无明显变化,而振动加速度幅值随电压的升高而升高。

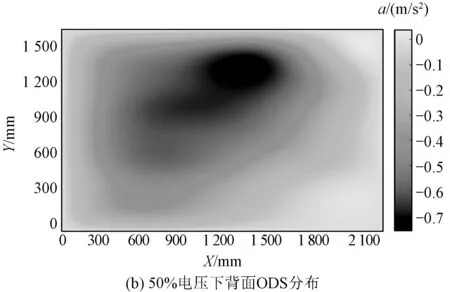

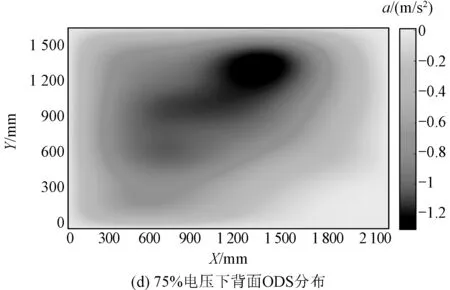

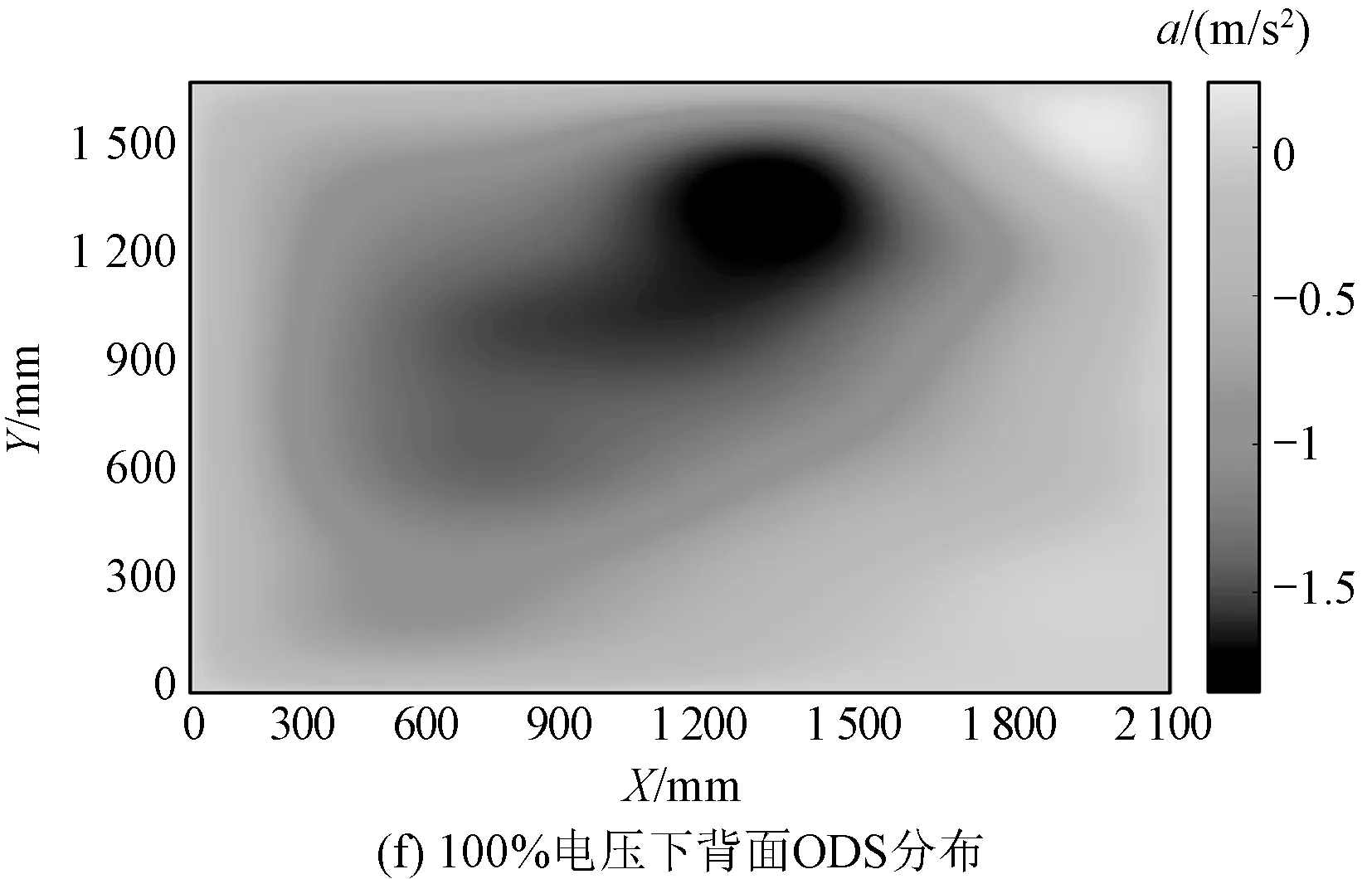
图9 正常状态下电抗器表面振动的100 Hz频率在不同电压下的ODS图像Fig.9 ODS image of reactor surface at 100 Hz frequency under different voltages
图10为电抗器表面振动的50 Hz频率分量在不同电压下的ODS图像,从图10中可见,在不同电压下,相同频率分量下的ODS分布相似,且振动加速度幅值随电压的升高而升高,而不同频率分量下的ODS图像差别很大。
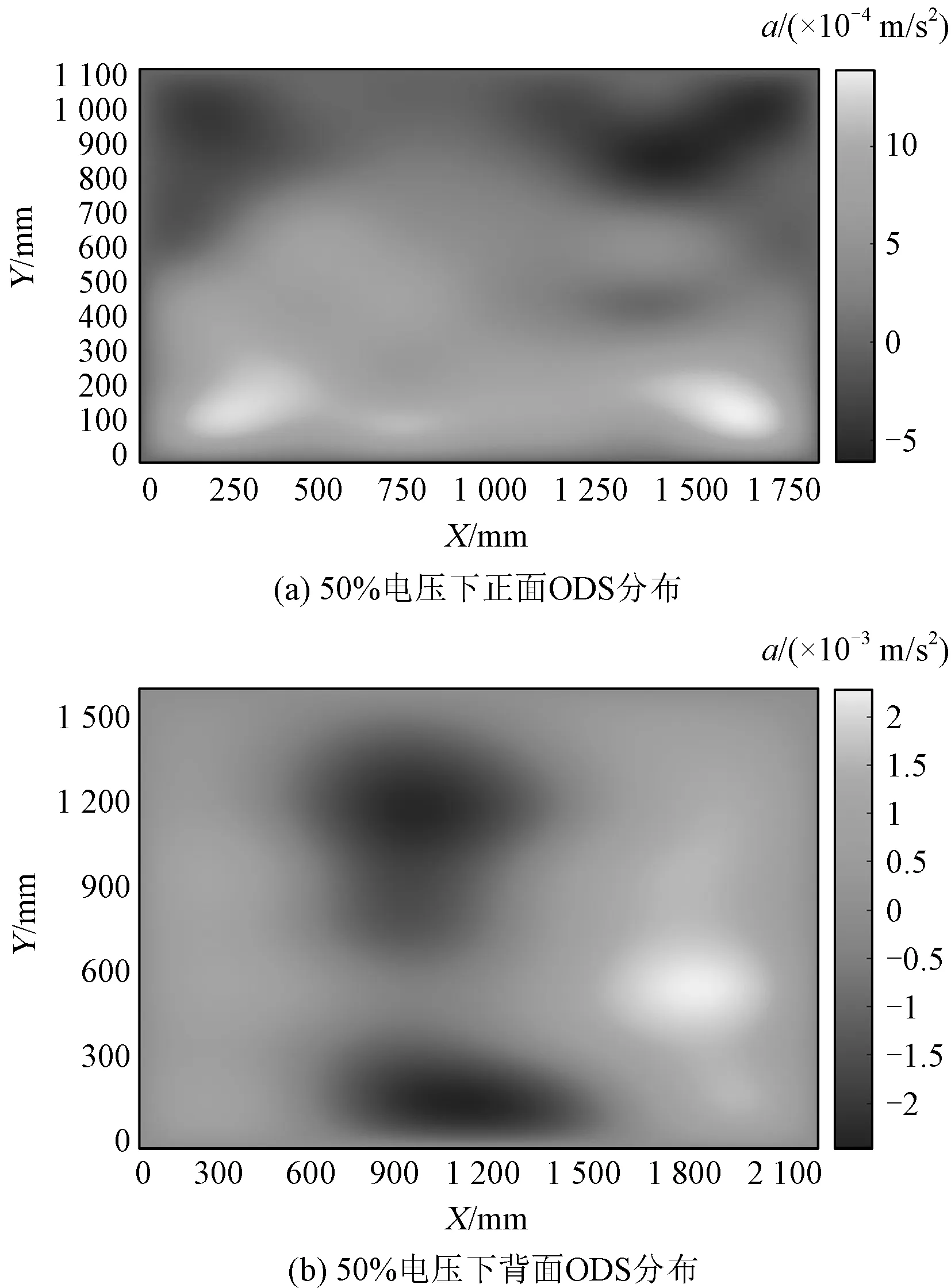
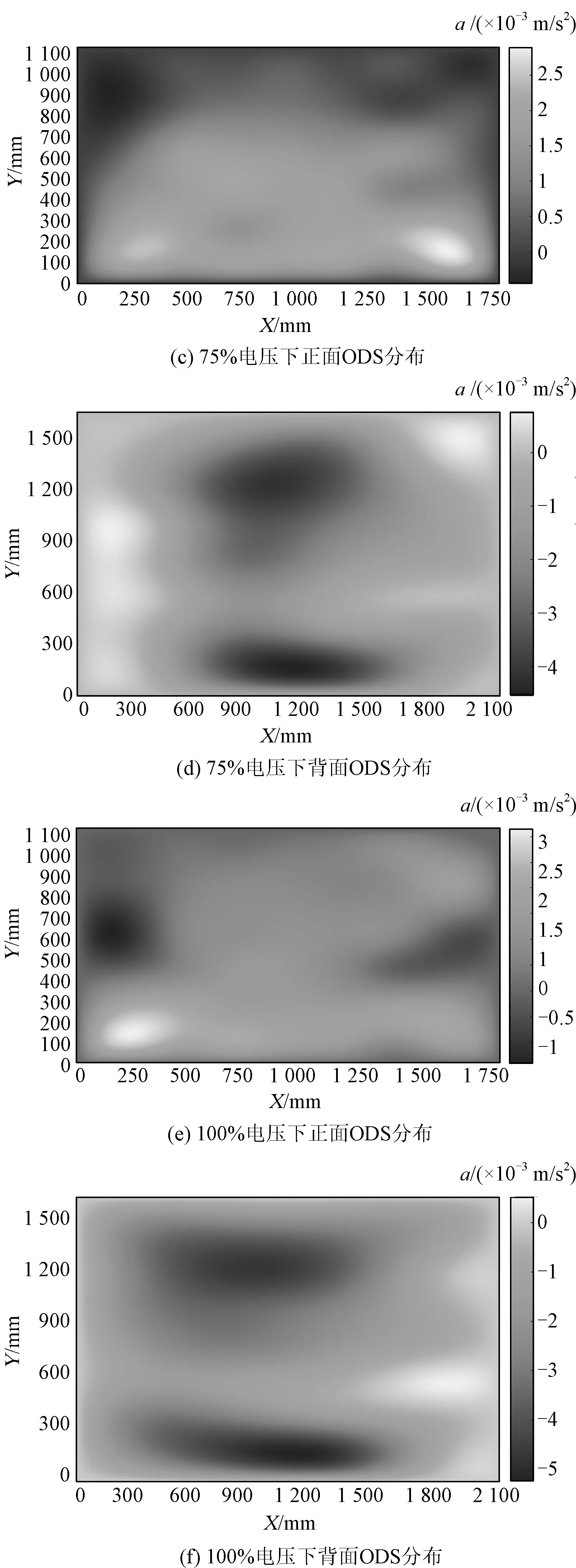
图10 正常状态下电抗器表面振动的50 Hz频率在不同电压下的ODS图像Fig.10 ODS image of reactor surface at 50 Hz frequency under different voltages
4.3 绕组松动实验
实验中,对电抗器的绕组进行人为松动,使其绕组压紧力降低至原有压紧力的90%。实验中选取箱体背面作为测量面,这是由于箱体背面相对平整,且距离内部铁心、绕组距离相对较近,因此该平面法相振动分布更能表现箱体内部结构件的机械状态;而套管侧由曲面构成,内部振动矢量在向外传播过程中相互影响,此外套管受迫振动不可避免地对该面振动信号造成干扰,因此本文以背面为例,采用灰度共生矩阵提取背面ODS图像纹理特征。图11为电抗器箱体背面。

图11 电抗器箱体背面Fig.11 Back of reactor box
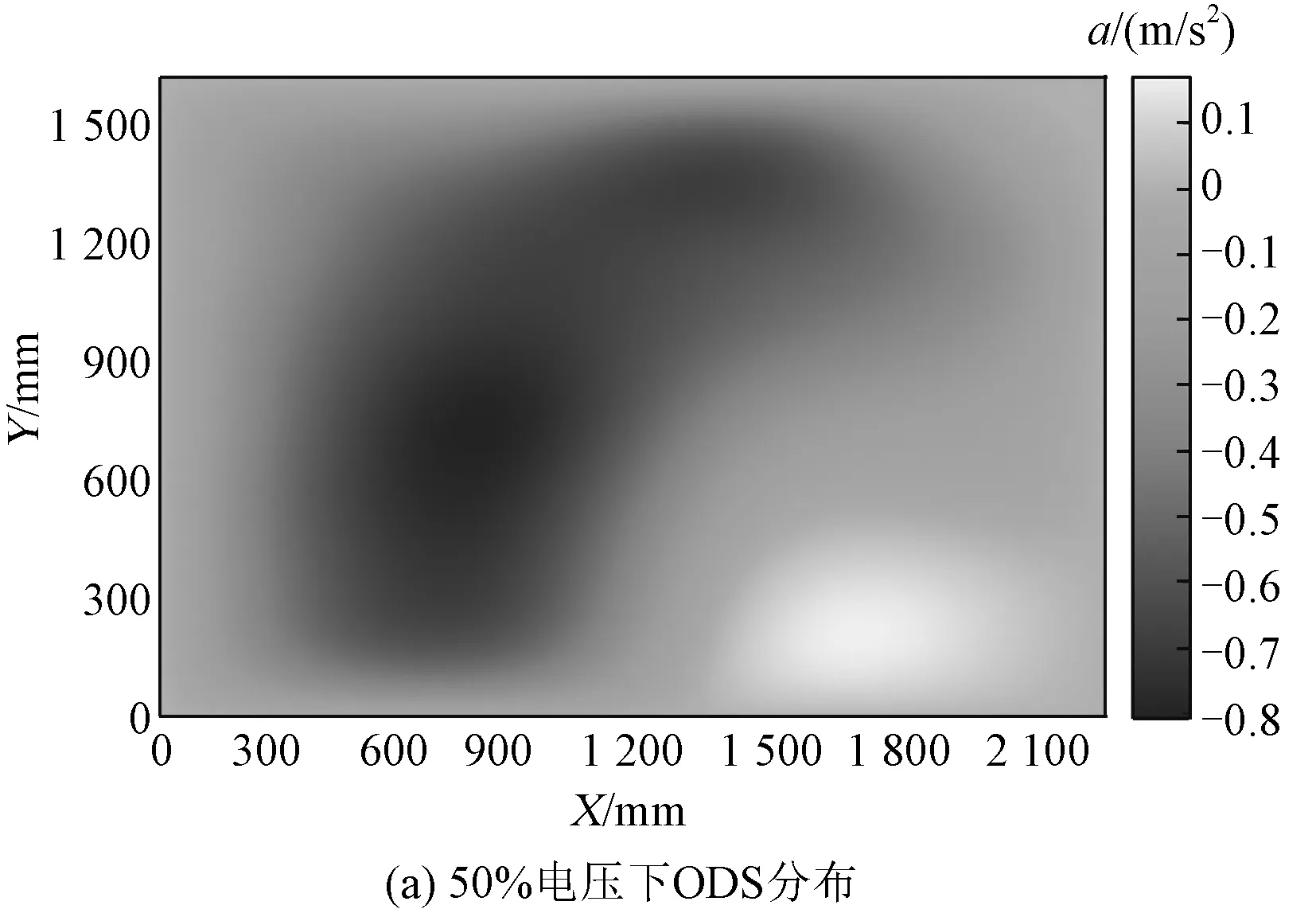
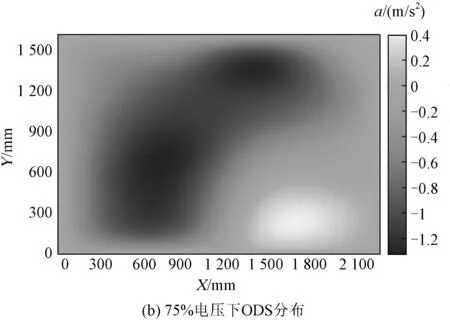
调整绕组至松动状态,重复升压实验,此时关于表面振动加速度和电压之间关系如图12所示。由图12可知,在绕组松动的条件下,ODS图像分布随电压变化无明显变化,而振动加速度幅值随电压的升高而升高。

图12 绕组松动状态下背面表面振动的100 Hz频率在不同电压下的ODS图像Fig.12 ODS image of reactor surface with winding loose at 100 Hz frequency under different voltages
由于绕组松动状态改变,通过电抗器内部结构件传递到油箱表面的振动也会随之发生变化,所得ODS图像也会有所不同,通过对比图9和图12所示两种不同运行状态下电抗器箱壁表面ODS图像,可以发现不同工况下的ODS图像有所不同,此时有必要引入特征值作为判断电抗器机械状态的依据,根据特征值的偏移程度来判断电抗器机械状态。
将ODS图像灰度化,并通过灰度共生矩阵的特征值来描述ODS图像的纹理变化。由于ODS并非某一时刻下的单一图片,而是描述结构上多个点相对振动状态的一种振动模型,因此可以通过一个周期内ODS的变化生成一个动图来描绘表面振动的动态特征。生成动图不但使得电抗器表面振动更为直观,而且也可以通过一个周期内不同时刻的ODS图像提取特征值,得到更加普遍的结论。电抗器表面振动的一个周期为0.01 s,取其中的4个时刻(t1、t2、t3、t4)进行分析。其中,t1=0.694 4 ms、t2=2.778 ms、t3=5.555 ms、t4=7.639 ms。
图13、图14为不同工况下不同时刻ODS的灰度图像。通过灰度图像,生成灰度共生矩阵,并提取特征值见表3。由表3可知:
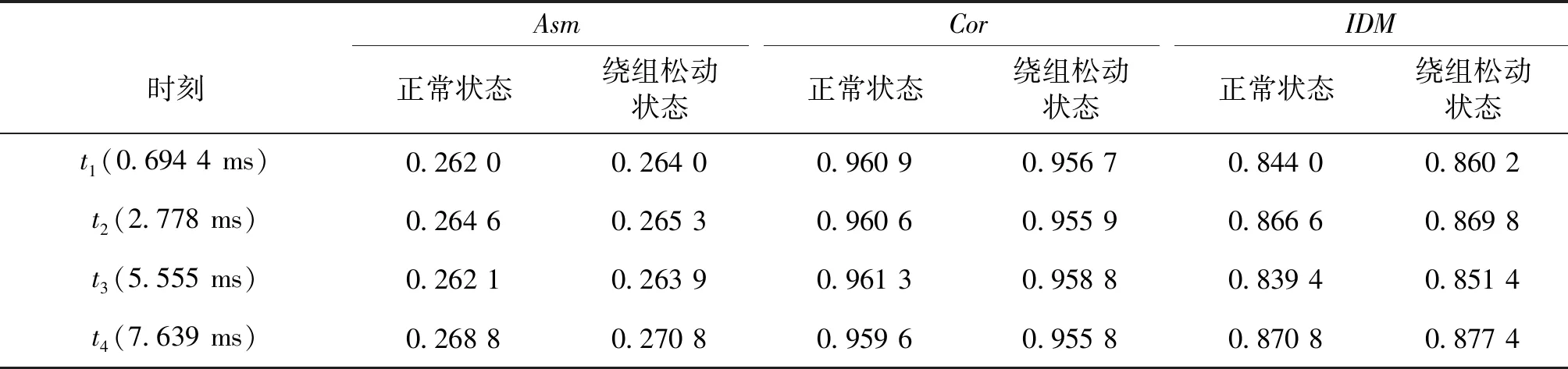
表3 不同工况下ODS特征值Tab.3 Eigenvalues of ODS under different conditions
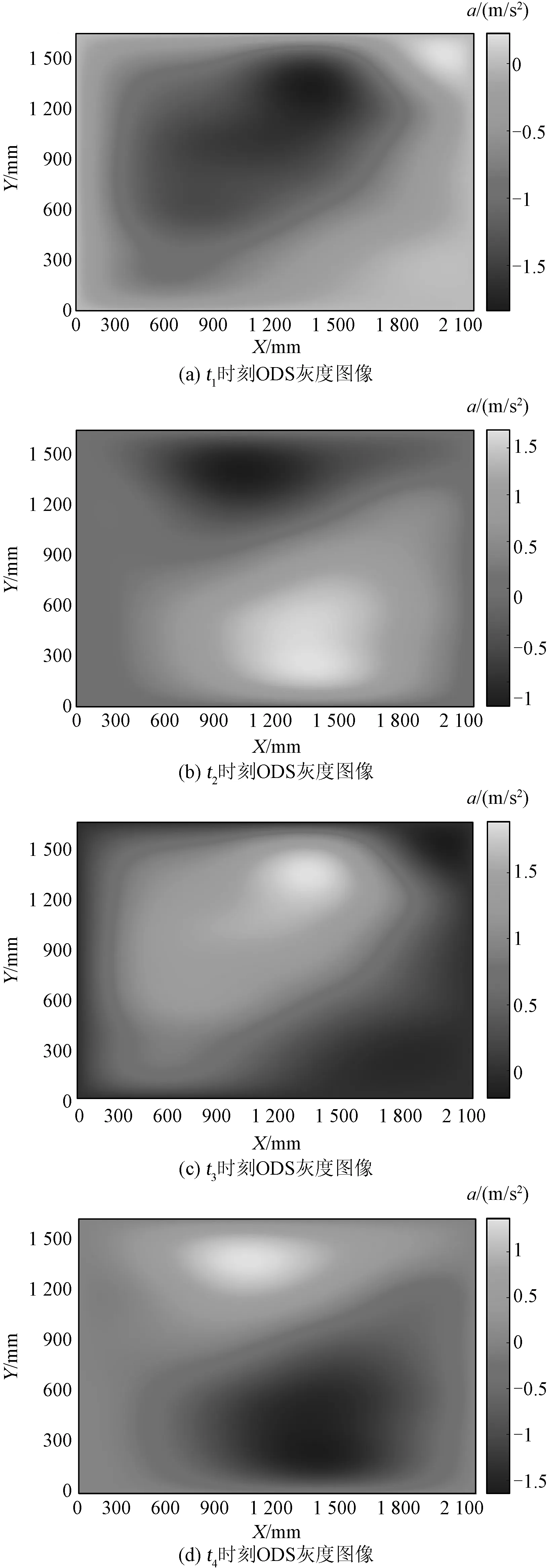
图13 正常状态下不同时刻ODS的灰度图像Fig.13 Grayscale images of ODS at different times under intact working condition
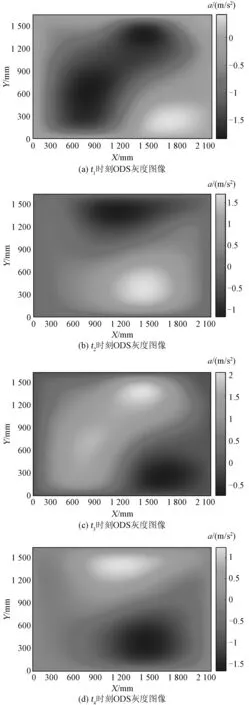
图14 绕组松动状态不同时刻ODS的灰度图像Fig.14 Grayscale images of ODS at different times under winding-loose working condition
(1)相比于正常状态,绕组松动状态下,其ODS图像的灰度共生矩阵的能量要高于正常状态。这说明了当绕组松动时,其ODS图像的均匀程度要低于正常状态,进而说明其振动分布也要更不均匀一些。
(2)相比于正常状态,绕组松动状态下,其ODS图像的灰度共生矩阵的相关性要低于正常状态。这说明了当绕组松动时,其ODS图像在行或列上的相似程度较低。
(3)相比正常状态,绕组松动状态下,其ODS图像灰度共生矩阵的逆差距要高于正常状态。这说明绕组松动状态下的ODS图像不同区域间缺少变化。
5 结论
本文以一台500 kV电抗器为研究对象,通过进行升压实验与绕组松动实验,得到了如下结论:
(1)在电抗器表面布置若干测点,通过相位校正,得到频域ODS图像,从而可以动态地反映电抗器表面各测点振幅的差异,ODS图像为电抗器振动形态提供了可视化效果。
(2)对于电抗器箱壁ODS图像而言,振动的幅值随工作电压的升高而增大,而振动相位不受工作电压的影响。
(3)通过灰度共生矩阵可以提取ODS图像中的纹理特征,通过绕组松动实验结果可以表明:与正常状态下的电抗器相比,绕组松动的电抗器ODS图像的能量升高,相关性降低,逆差距升高。
