燃煤机组烟气水分回收系统设计与运行最优化

2023-02-22贾晨辉

动力工程学报 2023年2期

贾晨辉，刘培，李政

(清华大学能源与动力工程系，电力系统国家重点实验室，北京 100084)

我国发电结构以火力发电为主，为保障能源安全，燃煤发电在未来能源系统的发展和转型中仍将发挥重要作用[1]。当前大部分燃煤电厂采用湿法脱硫技术，脱硫塔后的烟气携带大量水蒸气，水蒸气体积分数约为10%～13%，具有可观的节水潜力。开发燃煤电厂尾部烟气水分回收系统可缓解电厂用水压力，促进资源的综合利用[2]。

烟气水分回收技术主要有冷凝法、吸收法和膜冷凝法等。冷凝法使用冷凝器将烟气温度降低至水蒸气的露点温度以下，使烟气中的水蒸气凝结，冷凝器管束一般采用钢管[3]或氟塑料管[4]。吸收法将烟气与除湿溶液间的水蒸气分压力差作为驱动力，采用具有吸湿能力的溶液作为除湿剂，其与烟气直接接触进行烟气除湿[5]。设备腐蚀、除湿剂结晶以及系统成本高是制约吸收法发展的关键因素[6]。

在多种膜分离技术中，亲水性多孔陶瓷膜表现出良好的烟气水分回收性能，已有学者通过实验测试其水回收性能，并尝试将其应用于发电厂。相比于传统的冷凝法和吸收法，其具有回收水量大、回收水质好、传热性能高、结构简单、耐腐蚀等优点[7]。美国气体技术研究所研制了纳米多孔陶瓷膜，从烟气中提取水蒸气及其潜热，水回收率可达到40%～50%[8]。Li等[9]开发了用于燃煤电厂中试的多孔陶瓷膜冷凝器，水回收通量达43.65 kg/(m2·h)。Xiao等[10]建立了集总参数模型，揭示了陶瓷膜冷凝器中烟气水热回收过程的熵产情况。Li等[11]讨论了膜冷凝器的不可逆损失，并对工程设计进行了优化。杜紫薇等[12]采用多孔陶瓷膜回收烟气中的水分和余热，建立了耦合膜法烟气水热回收系统的全厂热力系统模型，并对系统进行了技术经济性分析。然而，目前针对多孔陶瓷膜的研究大多集中于机理验证和性能测试，膜冷凝器与燃煤机组烟气系统的集成和协同优化仍存在问题。

燃煤电厂尾部烟气流量、温度及水蒸气体积分数等条件随电厂负荷发生变化，导致烟气水分回收系统处于波动范围较大的运行条件中，影响水回收率与能耗。因此，综合电厂负荷条件对烟气水分回收系统进行集成优化成为必然选择。

数学规划是一种系统集成方法[13]，已被应用于换热网络[14]、质量交换网络[15]和其他过程系统。针对考虑运行波动性的系统集成优化，研究人员多采用基于情景的两阶段最优化方法，使用一组带有概率权重的情景表征运行的波动性，同时优化不随运行波动改变的系统设计变量及依据各情景特征波动的运行变量，获得使系统整体性能最优的设计与运行参数最优解。Saif等[16]建立了反渗透网络配置和运行参数的两阶段最优化模型，获得了最优系统结构和随时间变化的运行参数。张帅[17]建立了基于情景的两阶段随机规划模型，以实现不确定条件下碳税政策和碳捕集与封存技术的耦合。

为实现膜冷凝器设计运行与燃煤机组尾部烟气系统的匹配集成，笔者提出了一种基于负荷情景的烟气水分回收系统设计-运行两阶段最优化方法，以某330 MW燃煤机组为案例，计算水分回收系统的最优化方案，研究了燃煤机组负荷特点对膜冷凝器结构尺寸和运行参数最优值的影响。

1 燃煤机组尾部烟气水分回收系统

燃煤机组尾部烟气水分回收系统由脱硫塔、陶瓷膜冷凝器、循环水泵等部件组成，其结构示意图见图1。从锅炉排出的烟气进入脱硫塔，在脱硫塔中蒸发并携带大量水蒸气，从脱硫塔排出的饱和烟气进入膜冷凝器。在膜冷凝器内，烟气与膜管发生对流换热，水蒸气冷凝至膜管表面，烟气流出膜冷凝器后经烟囱排出。膜管壁的冷凝水在压差驱动下穿过膜管，与在管束内侧流动的循环冷却水混合。循环冷却水在膜冷凝器内吸收热量、与冷凝水混合后流出膜冷凝器，一部分输送至脱硫塔作为补水，其余部分换热后再次进入膜冷凝器进行循环。

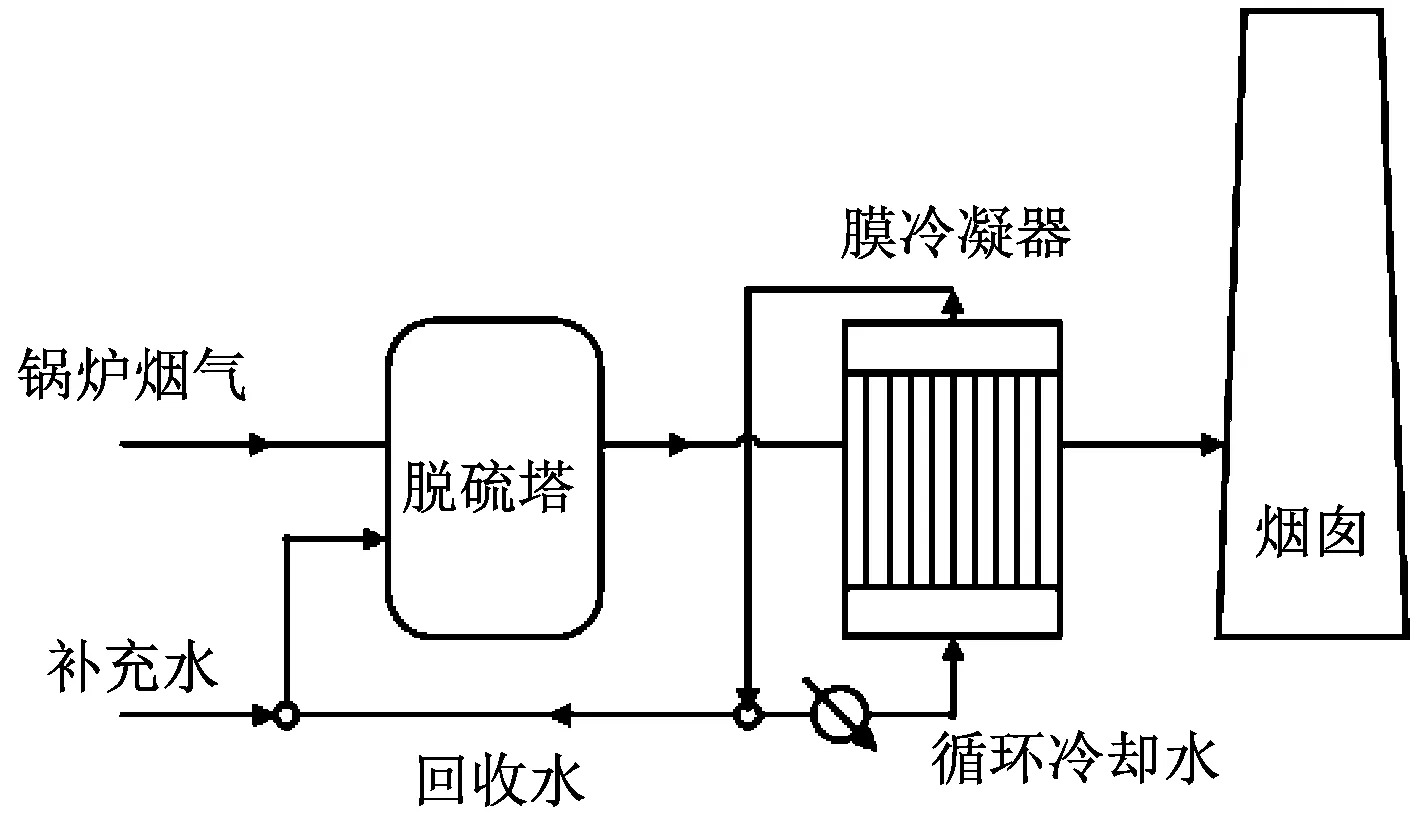
图1 燃煤机组尾部烟气水分回收系统示意图

陶瓷膜冷凝器是系统的核心设备，其结构如图2所示。陶瓷膜冷凝器由叉排排列的复合陶瓷膜管组成，烟气在管外掠过，冷却水在管内流动。复合陶瓷膜管是多孔材料，水分可以从管外经过微孔渗入管内。

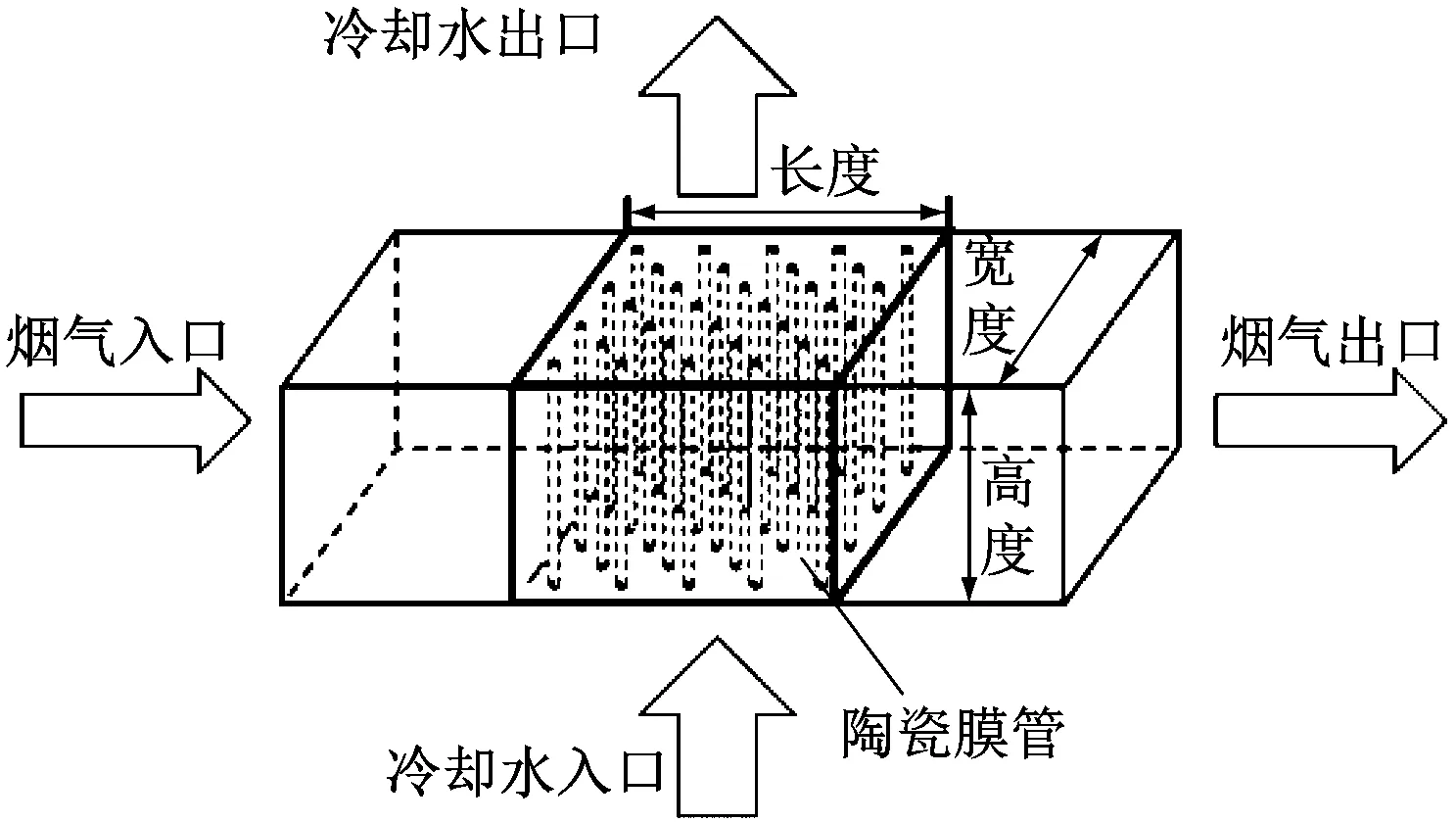
图2 陶瓷复合膜冷凝器结构示意图

进入该系统的烟气参数随机组负荷的变化而变化，为满足水回收率要求，需对膜冷凝器的结构尺寸、循环冷却水质量流量等参数进行最优化设计。

2 研究方法

图3为燃煤机组烟气水分回收系统设计与运行最优化计算流程，通过对负荷变化特点进行分析，生成一系列负荷情景，综合计算各情景下烟气水分回收系统的性能表现，求解系统设计与运行参数的最优解。

图3 燃煤机组烟气水分回收系统设计与运行最优化计算流程

2.1 情景生成模块

情景生成模块包含负荷分布估计模型和烟气负荷关联模型。负荷分布估计模型依据机组的历史负荷数据给出机组典型负荷区间及其出现的概率。烟气负荷关联模型用于计算给定机组负荷下的尾部烟气参数。综合上述信息生成多个情景，每个情景包含机组负荷、烟气参数信息及情景出现的概率。负荷分布估计模型以一段时期内机组的历史运行数据为输入，统计该时间段内燃煤机组发电负荷的频率分布情况，得到一组典型的负荷区间及其随时间的出现频率，将其作为发电负荷概率分布的估计。烟气负荷关联模型基于锅炉热力计算及煤质分析数据得到各设计工况下锅炉尾部烟气的参数。

尾部烟气体积流量受锅炉耗煤量、煤质参数及过量空气系数控制。1 kg燃料完全燃烧所需的理论空气量为：

(1)

式中：w(Car)、w(Har)、w(Sar)、w(Oar)分别为设计煤种收到基碳、氢、硫、氧元素的质量分数，%；V0为理论空气量，m3。

过量空气系数为1时，燃料完全燃烧后产生的烟气体积(即理论烟气量)为：

(2)

式中：V0,y为理论烟气量，m3；VCO2、VSO2、V0,N2、V0,H2O分别为燃料完全燃烧后二氧化碳、二氧化硫、氮气、水蒸气的体积，m3；w(Nar)、w(Mar)分别为设计煤种收到基氮元素的质量分数和水质量分数，%；d为空气含湿量，g/kg。

在过量空气系数α大于1时，实际烟气量Vy为：

Vy=V0,y+(α-1)V0(1+0.001 61d)

(3)

根据各负荷下锅炉燃料消耗量、空气预热器出口处的过量空气系数和温度，通过曲线拟合获得尾部烟气量、温度及其成分随机组负荷的关联公式。

2.2 基于部件传热传质机理的水回收系统模型

烟气在脱硫塔中发生的热力学过程可视为绝热增湿过程，即塔内烟气焓基本不变，含湿量不断增加，烟气在出塔口为饱和状态，水蒸气的分压等于当前烟气温度下的饱和蒸气压。脱硫塔进出口烟气能量平衡过程为

qm,H2O,FGD[cp,H2O,FGD(tg,FGD,out-tw,FGD,in)+γ]=

qm,g,FGD,incp,g(tg,FGD,out-tg,FGD,in)

(4)

式中：qm,H2O,FGD为烟气在脱硫塔内吸收的水质量流量，kg/s；cp,H2O,FGD为脱硫塔补水的比定压热容，kJ/(kgK)；tw,FGD,in为脱硫塔补水温度，℃；γ为水的蒸发潜热，kJ/kg；qm,g,FGD,in为进入脱硫塔的烟气质量流量，kg/s；cp,g为烟气在脱硫塔内的平均比定压热容，kJ/(kg·K)；tg,FGD,in和tg,FGD,out分别为脱硫塔入口与出口处的烟气温度，℃。

膜冷凝器内同时发生传热与传质过程。冷凝水在膜管表面的渗透过程满足式(5)。

qm,rec=JSmo

(5)

式中：qm,rec为膜冷凝器冷凝水质量流量，kg/s；J为膜冷凝器管束平均渗透通量，kg/(m2·s)；Smo为膜冷凝器膜管的外表面积，m2。

冷凝水质量流量在烟气侧和冷却水侧满足质量平衡。

qm,g,in=qm,rec+qm,g,out

(6)

qm,c,in+qm,rec=qm,c,out

(7)

式中：qm,g,in和qm,g,out分别为烟气在膜冷凝器入口和出口的质量流量，kg/s；qm,c,in和qm,c,out分别为循环冷却水在膜冷凝器入口和出口的质量流量，kg/s。

水回收率η为：

(8)

式中：qm,g,H2O为烟气在膜冷凝器入口处的水蒸气质量流量，kg/s。

膜冷凝器烟气侧对流传热量Φg、冷凝水放热量Φw、膜管壁导热量Φm、冷却水吸热量Φc计算分别见式(9)～式(12)。其中，管壁的导热忽略了管壁表面的污垢热阻。

Φg=hgSmo(Tg-Tmg)=qm,g,incp,g(Tg,in-Tg,out)

(9)

Φw=qm,recγ

(10)

(11)

Φc=hcSmi(Tmc-Tc)=qm,c,incp,c(Tc,out-Tc,in)

(12)

式中：Smi、Sm分别为膜管的内表面积和平均表面积，m2；cp,c为冷却水比定压热容，kJ/(kg·K)；hg、hc分别为烟气、冷却水与膜管之间的对流传热系数，kW/(m2·K)；Tg、Tmg、Tmc、Tc分别为膜冷凝器内烟气、膜管外壁、膜管内壁和冷却水的平均温度，℃；Tg,in、Tg,out分别为膜冷凝器的烟气入口和出口温度，℃；Tc,in、Tc,out分别为膜冷凝器的冷却水入口和出口温度，℃；λm为膜管热传导率，kW/(m·K)；do、di分别为膜管外径和内径，m。

对于多孔陶瓷膜，基于组成材料和孔隙率计算其平均热传导率。

λm=τλH2O+(1-τ)λm0

(13)

式中：τ为膜管孔隙率；λH2O、λm0分别为水和陶瓷材料的热传导率，kW/(m·K)。

换热量之间遵循能量守恒方程。

Φg+Φw=Φm=Φc

(14)

膜管数量、管束排列间距、管径大小等结构参数决定了烟气和冷却水在组件内的通流形态和流动速度，进而影响烟气侧和水侧的对流换热及传质过程。依据烟气与管束、冷却水与管束的对流换热条件，分别选择合适的换热关联式计算膜冷凝器烟气侧和冷却水侧的Nusselt数[18]，通过Nusselt数将流动过程与换热过程关联。

(15)

(16)

式中：Nug、Nuc分别为烟气侧、冷却水侧的Nusselt数；λg、λc分别为烟气、冷却水的热传导率，kW/(m·K)。

对于烟气侧传热过程，当烟气雷诺数Reg范围在103～2×105时，选择文献[19]中推荐的关联式进行计算。

(17)

(18)

式中：Prg、Prmg分别为烟气主流和管束外壁处的普朗特数；ε为管排修正系数；s1、s2分别为管束横向和纵向间距，m。

对于冷却水侧的传热过程，在冷却水雷诺数Rec>2 300时，水流处于湍流状态，计算时使用文献[20]中推荐的关联式。

(19)

fc=(1.82ln(Rec)-1.64)-2

(20)

式中：Prc、Prmc分别为冷却水主流、管束内壁处的普朗特数；fc为管内水的摩擦因数；H为管长，m。

依据奇尔顿-柯尔本类似准则，管外烟气中水蒸气向管壁表面的传质扩散过程与对流换热过程类似，表征传质过程的Sherwood数与表征对流传热过程的Nusselt数满足以下关系：

(21)

式中：Shg为烟气的Sherwood数；Leg为烟气的Lewis数。

膜管外水蒸气的传质系数kg和膜冷凝器管束平均渗透通量J分别为：

(22)

J=kgρg(ωg-ωmg)

(23)

式中：Dg为烟气的质量扩散率，m2/s；ρg为烟气平均密度，kg/m3；ωg、ωmg分别为烟气主流、管束外壁处水蒸气的质量分数。

在管束外壁的气液界面上，水蒸气与凝结液近似处于气液相平衡状态，因此可依据Antoine方程计算管束外壁的水蒸气分压，进而得到管束外壁的水蒸气质量分数。

(24)

(25)

式中：pmg,sat为管束外壁的饱和蒸气压，kPa；MH2O、Mg分别为水和烟气的摩尔质量，g/mol。

2.3 设计-运行两阶段最优化数学模型

图4给出了设计-运行两阶段最优化模型的主要设置。模型包含两类待优化变量，一类是不随运行情景的改变而变化的设计变量，包括膜管内外径、横纵管间距以及膜冷凝器尺寸；另一类是随情景的改变可能发生变化的运行变量，包括每个负荷情景下循环冷却水的流量、温度等。

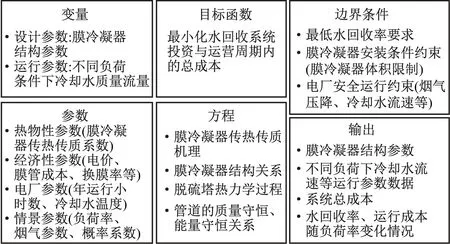
图4 设计-运行两阶段最优化模型主要设置

模型以系统寿命周期内总成本最低为目标函数z，总成本包含设计阶段的建设投资成本Cc和运行阶段的运行维护成本Co。

z=Cc+Co

(26)

投资成本为膜冷凝器的制造成本和辅助成本Caux。

Cc=SmPm+Caux

(27)

式中：Pm为膜管单价，元/m2。

运行成本为系统寿命周期内用电成本和膜冷凝器的维护成本(换膜成本)，对各情景下系统运行情况进行加权求和。

(28)

式中：Wfan,t和Wpump,t为情景t下烟气侧引风机及冷却水侧水泵消耗的电功率，kW；Pt为情景t发生的概率；De为电价，元/(kW·h)；Uhour为燃煤机组运行小时数，h/a；βm为膜冷凝器换膜率；L为膜冷凝器的设计寿命，a。

模型方程包括了部件机理模型方程、各流股的质量和能量守恒以及部件与流股之间的连接关系方程。模型的边界条件包括水回收率要求、系统物理约束及运行安全要求。

对于每个情景，水回收率ηt应不小于烟气水回收率目标值η0。

ηt≥η0

(29)

受场地限制，水回收系统的设计尺寸有所限制。

Vm≤Vm,max

(30)

式中：Vm为膜冷凝器的体积，m3；Vm,max为场地所限的最大体积，m3。

运行过程中，烟气和冷却水在冷凝器内的流动阻力ΔPg,t和ΔPc,t均不应超过其流动阻力给定值ΔPg,max和ΔPc,max。

ΔPg,t≤ΔPg,max

(31)

ΔPc,t≤ΔPc,max

(32)

模型的输出为水回收系统膜冷凝器结构尺寸参数、各负荷情景下冷却水运行参数的最优值，以及水回收系统的水回收特性、成本等性能指标。

该模型是一个非线性模型，采用GAMS软件进行编程，并使用最优化求解器进行求解。

3 案例设置

以我国北方1台330 MW亚临界燃煤机组为研究对象进行案例分析，锅炉设计煤种采用质量占比为67%大同煤和质量占比为33%宣东煤的混煤，基于电厂分布式控制系统的历史发电数据对负荷分布情况进行统计。膜冷凝器膜管材料选择平均孔径为1 μm的α-Al2O3复合陶瓷膜，孔隙率为0.4。

考虑到模型求解的复杂度，流体热物性参数均取参考温度范围内的平均值，表1给出了相关取值。

表1 热物性数据

情景生成模块共生成6个情景，表2给出了每个情景对应的关键负荷、概率和烟气特性。表3总结了两阶段最优化模型的详细设定，包括电厂运行约束和经济性参数。为进行对比分析，本文以单一情景(100%热耗率验收工况)对烟气水分回收系统进行最优化计算，并将计算所得的系统结构参数代入多情景模拟运行中，作为两阶段最优化结果的参考。

表2 情景数据

表3 最优化模型参数设定

4 结果分析与讨论

两阶段最优化方案和参考方案中的膜冷凝器结构参数如表4所示。与参考方案相比，两阶段最优化方案中的膜冷凝器内外径和管间距更大；膜管数量为5 834，比参考方案少11.3%；膜面积为4 398.7 m2，比参考方案少3.2%。这有利于减少膜冷凝器的投资和维护成本。

表4 膜冷凝器设计参数结果

两阶段最优化方案和参考方案的运行参数如图5所示。在不同情景下，两阶段最优化方案通过调节冷却水质量流量来保证水回收率达标，同时可降低循环水泵的电功率；参考方案中冷却水质量流量不对负荷做出响应，在低负荷条件下冷却水质量流量保持高位，虽然会使水回收率更高，但也导致循环水泵的电功率更大。

(a) 循环冷却水质量流量

此外，在100%负荷条件下两阶段最优化方案的冷却水质量流量、引风机和循环水泵消耗的电功率均高于参考方案，说明两阶段最优化方案的膜冷凝器结构在该负荷下并不处于最优运行状态，但综合考虑负荷变化特性，两阶段最优化方案的管径和间距更大，使其运行过程中阻力减小，引风机和循环水泵的电功率降低，展现出更优的性能。两阶段最优化方案的平均功率为167.4 kW，比参考方案降低12%。

图6为两阶段最优化方案和参考方案的成本对比情况。在系统寿命周期内两阶段最优化方案的总成本为3 598.8万元，参考方案的总成本为3 930.3万元，两阶段最优化方案总成本较参考方案降低8%。其中，投资成本降低3%，运维成本降低12%。在运维成本中，用于更换膜材料的维护成本降低4%，用于驱动系统运行的用电成本降低30%。