数值线性代数算法在工程软件中的应用与意义

卢靖程

北京市八一学校 北京 100000

引言

高级计算机体系结构对科学计算领域有着重要影响，包括算法研究和数值线性代数软件。线性代数，特别是对于线性方程求解，有着重要的地位。如果一个矩阵有着大量的0元素，那么这个矩阵被称为稀疏矩阵。

为了研究如何提高机计算机体系结构计算效率，研究人员做了大量的工作。在本篇文章中，我们主要关注两个问题：①工作目的；②使用线性代数建立模块；③算法设计和并行实；④未来的研究方向。克莱因和LU因式分解作为计算稠密矩阵的典型方法，我们将在设计高级计算机体系结构的线性代数计算软件中作为重点[1-5]。Cholesky和LU分解是非常重要的数值线性代数算法。这些是高级架构计算机设计线性代数软件时必须考虑的最重要的因素。数值线性代数算法不仅因为会使得复杂工程问题变得相对简单，同时还因为正是这些算法才使得没有闭形式解的方程得出近似解。这些应用包括电磁散射和计算动力学问题。在过去的15年左右，在解决线性代数问题的算法和软件领域研究人员取得了大量的成果。实现跨平台可移植的高性能代码的目标在很大程度上是通过线性代数核的识别实现的，即基本线性代数子程序（BLAS），以及BLAS的连续级别表示的EISPACK、LINPACK、LAPACK和ScaLAPACK库[6-10]。我们为高级架构计算机设计线性代数算法的方法的关键见解是，为了获得高性能，数据在不同的内存层次之间移动的频率必须最小化。因此，我们在实现中同时利用向量化和并行化的主要算法方法是使用块划分算法，特别是与执行矩阵-向量和矩阵-矩阵操作的高度调优的核一起使用（Level 2和Level 3 BLAS）。在计算机领域可利用诸如MATLAB，MATHEATICA等软件来进行一些数学问题的计算，分析和大量的模拟。其中MATLAB被广泛地运用到线性代数的计算中，具有数值分析和一些符号的计算、工程学方面与科学绘图、数字图像处理、财务计算与金融工程等功能。而MATHMATICA更多地被用在作图，模型建立等方面。下图的图像由8×8=64个像素点组成。每个像素的值在0到255的范围内。值0表示纯黑色的像素，255表示纯白色的像素。如果我们更进一步来去看的话，m×n图像可以由具有m行和n列的2D矩阵表示，其中每个单元格包含相应的像素值：

图1 由线性代数生成的像素图片

综上所述，线性代数还具有利用矩阵生成图片的功能，每个图像可以被认为是由3个2D矩阵表示，对于彩色图片有相对应每个R，G，B通道各一个。R通道中的像素值0表示红色的零强度，255表示红色的全强度。以此来合成，编译与转录图片。

2 主要工作

2.1 一些关于矩阵的相关概念

2.1.1 行矩阵、列矩阵：在一个m×n阶的矩阵中，m的值为1，称为行矩阵，也被称为n维行向量;n的值为1，称为列矩阵，也被称为m维列向量。

2.1.2 零矩阵：矩阵中所有元素都为0的m×n阶矩阵。

2.1.3 n阶方阵：对于m×n阶矩阵A中，当m=n时，可定义行列式记为|A|；主对角线及主对角线元素存在于n阶方阵中。

2.1.4 单位矩阵：当矩阵中主对角线上的元素都为1，其余元素均为0的n阶方阵称为n阶单位矩阵，记为In。

2.1.5 对角形矩阵：不是主对角线上的元素全部等于0的n阶方阵称为对角形矩阵。

2.1.6 同型矩阵：若两个矩阵A与B行列数皆相同，这两个矩阵就是同型矩阵。

2.1.7 转置矩阵：将一个矩阵A的行上的元素与列上的元素在不改变排列顺序的情况下互换，记为：

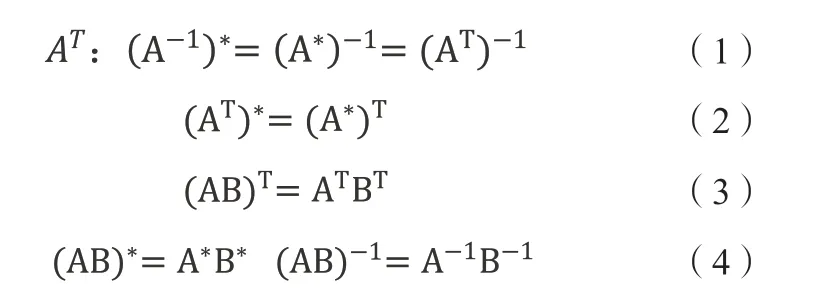
2.1.8 对称矩阵与反对称矩阵：一个n阶方阵A，如果A的转置矩阵等于A，那么则称A是一个对称矩阵。如果A的转置矩阵等于-A，那么则称A为反对称矩阵。

2.1.9 逆矩阵：一个n阶方阵A，如果有一个n阶方阵B，使得AB等于BA等于单位矩阵，则B称为A的逆矩阵，记为

2.1.10 伴随矩阵：设矩阵A，Aij为行列式A中元素aij的代数余子式，称A*为矩阵A的伴随矩阵。AA=A*A=|A|I。

2.1.12 正交矩阵：设A为实数R上的矩阵，如果它满足则称A为正交矩阵。

2.1.13 矩阵的初等变换：互换、倍乘、倍加。矩阵的对于初等行的变换和对于初等列的变换被统称叫做矩阵的初等变换。

2.1.14 阶梯形矩阵：若矩阵A满足两条件：条件一：若存在元素全为0的行，则该行应在最下方；条件二：非零行的第一个不为零的元素的列标号随行标号的增加而严格逐渐增加，满足两条件则称此矩阵A为阶梯形矩阵。

2.1.15 一些矩阵的基本性质-秩的性质。

2.1.16 对于rank（X+Y）= rank(X)+rank(Y)的条件的证明。

首先，显然有rank(X+Y) ≤ rank(X)+rank(Y).我们先证明（X+Y）X=0可以推出AX = 0且BX = 0，0=A（X+Y）X =A^2X，由于rank(X^2) = rank(X)且任意AX=0的解为A^2X = 0的解，我们有AX=0与A^2X=0的解空间相等，于是A^2X=0推出AX = 0，此时当然有BX = 0.由于rank(X^2) = rank(X)，记rank(X) = r，故X^2中有r列线性无关，记为列，考虑XX’，其中X’为与X的列，由题意rank(XX)’= r，故r≥rank(X)’≥rank(XX)’=r，所以有至少r个线性无关的向量使得BX=0而AX≠0，从而rank(X)-rank(Y)，从而rank(X+Y) ≥ rank(X)+rank(Y)，故rank(X+Y) = rank(X)+rank(Y)。

3 稠密线性代数算法

因此，我们需要确定3个的线性代数操作步骤：

第一步：向量-向量运算，如更新y←y + x和内积d = xTy。

这些操作涉及(当向量长度为n时)O(n)和O(n)次计算。

第二步：矩阵-向量运算，比如矩阵-向量乘积y = Ax。这是一个O(n2)数据量的O(n2)次运算。

第三步：矩阵-矩阵运算，比如矩阵-矩阵乘积C =AB。这是一个O(n2)数据量的O(n3)次运算。

BLAS级别2和3的操作可以分别使用双嵌套循环和三嵌套循环来实现。通过简单的修改，这意味着对于第2级，每个算法有两个，而对于第3级，有6个不同的实现。关于第二和第三层的计算可以通过二层和三层嵌套循环实现。通过简单的调整，这意味着第二层有2个，第三层有6个算法。

虽然就操作数量而言，这两种实现是相同的，但由于体系结构的考虑，在性能方面可能存在很大的差异。例如，我们注意到，第一个实现中的内部循环使用L行，而第二个实现中的内部循环则遍历一列。由于矩阵的行或列通常存储在相邻的位置，列存储的历史默认值继承自FORTRAN编程语言，因此两者的性能可能完全不同。大型密集线性系统的一个主要来源是涉及边界积分方程的解的问题。这些是在感兴趣区域边界上确定的积分方程。

4 讨论

所有有实际意义的例子都是在二维边界上计算某个中间量，然后利用这个信息在三维空间中计算所需的最终量。将三维空间替换为二维空间的代价是最初的O(n3)变量的稀疏问题被O(n2)变量的密集问题所取代。

密集线性方程组在许多领域都有应用，包括：机翼设计；雷达截面研究；船舶和其他岸上设施周围的船坞；固体在液体中的溶解；降噪；光线通过小颗粒的扩散。

电磁学领域是密集线性系统求解器的主要用户。这个团体特别感兴趣的是解决所谓的雷达截面问题。在这个问题中，一个固定频率的信号从一个对象反射回来；目标是确定反射信号在所有可能方向上的强度。根据具体的问题，基本的微分方程可能会有所不同。在隐身飞机的设计中，最主要的方程是亥姆霍兹方程。为了求解该方程，研究人员使用矩量法。在流体流动的情况下，问题通常涉及求解拉普拉斯方程或泊松方程。在这里，边界积分解被称为面板法，得名于离散和近似一个结构，如飞机的四边形。一般来说，这些方法被称为边界元方法。这些方法的使用产生了大小为O(N)×O(N)的密集线性系统，其中N是使用的边界点（或面板）的数量。看到3N×3N大小并不奇怪，因为每个边界元素有3个物理量。

解决这类系统的一个典型方法是使用逻辑单元分解。矩阵的每一项都计算为两个边界元的相互作用。通常，必须计算许多积分。在许多情况下，计算矩阵所需的时间要比求解所需的时间大得多。隐身技术的建设者对雷达截面感兴趣，他们正在使用直接高斯消去方法来求解密集线性系统。这些系统总是对称的和复杂的，但不是厄米的。对于线性系统的解决方案，需要考虑系数矩阵。任何直接方法都是高斯消元法的一种变体。如上所述，对于稀疏矩阵，它位于包含非零元素的带中。为了最小化分解所需的存储，研究集中在寻找合适的矩阵排序。在许多情况下，通过矩阵的对称置换对方程进行重新排序不会改变系统的数值属性，并且可能会大大节省存储空间。通常，直接方法不利用线性系统的数值特性，因此它们的执行时间主要受输入矩阵的结构特性的影响。与其尝试通过减少带宽来最小化填充，不如尝试一种直接的方法。“嵌套剖析”排序递归地将矩阵图一分为二，从而将其分成不相交的子图。更准确地说，给定一个图，该算法依赖于“分隔符”的存在：一组节点，使得其他节点落入两个相互不连接的子图中。首先分解这些子图，然后分解分隔符的填充，可能低于其他排序。可以看出，对于二维空间维度的偏微分方程，存储要求在矩阵本身的对数因子内，即非常接近最优值。这个方法对于矩形网格上的偏微分方程很容易，但是如果有细致网格结构，它可以被进一步被推广。然而，对于3个空间维度的问题，嵌套剖分方法不再是最优的。解剖型方法的一个优点是它们会导致大量的非耦合矩阵问题。因此，在一定程度上，这些方法的并行化很容易。但是，树中较高级别的节点很快就会少于可用处理器的数量。除此之外，它们也是算法中较大的子问题，从而使方法的并行化复杂化。另一个实际问题是分隔符组的选择。在典型情况下，这是微不足道的，但在实践中，特别是并行时，这是一个严重的问题，因为两个结果子图的平衡取决于这个选择。最近，所谓的“第二特征向量方法”为此变得流行。

5 结束语

线性代数作为一种基础的数学工具，通过对几何的解析，线性代数能够被进行具体的表示。线性代数主要的研究数学对象对象：向量和方程还有矩阵。这三者的关系非常密切，所以我们在掌握一种理论的时候，应该套用其他曾经学习过的知识来帮助转移其中的理论，这是学习线性代数时需要掌握的一项重要技能。线性代数作为一种重要的数学工具，体现了数学中的一些思想。比如说线性代数中行列式的公式展开证明就可以从某些更简单的情况开始论证。线性代数中的内容也与高等数学中的一些内容不谋而合，可以与其他学科甚至建立联系，只要建立联系线性代数的学习，就不会像原来那么琐碎，会将知识形成一整个体系。在线性代数的学习中我们应该努力提高自己的分析能力与并且做到知识点的衔接与联系、转换。总的来说，对于线性代数的知识，它的逻辑性、严密性还有实用性都非常强，对于学习线性代数，必须要把线性代数的内在联系搞清楚，完全理解所学知识，并将其应用到实际生活中，这样也许才能真正理解线性代数。在现实生活中，我们要学会运用线性代数做到解决生活中的问题和一些事情。如本文所述，在具体工程计算中，直接方法具有一些令人满意的计算特性。最重要的是，他们解决问题的时间是可以预测的，无论是先验的，还是在确定矩阵排序之后。这是因为该方法不依赖于系数矩阵的数值性质，而仅依赖于其结构。另一方面，占用内存可能很大，随之而来的是执行时间。对于大型应用程序，实际大小问题的存储要求可能会令人望而却步。在未来，我们将进一步讨论直接法形成对比的迭代法，迭代方法的存储需求要低得多。通常，存储和每次迭代的成本是矩阵存储的数量级。然而，迭代次数很大程度上取决于线性系统的属性，并且最多只能知道一个阶估计；对于困难的问题，由于局部误差的积累，这些方法甚至可能不会收敛。在某种的意义上，每次迭代中的迭代方法定位问题解的近似值，测量近似值与真实解之间的误差，并基于误差测量通过构造下一次迭代来改进近似值。这个过程重复，直到误差测量被认为足够小。