改进型预测函数在并联DC-DC中的应用
2023-02-21伍孟涛王海生闫小宇葛芦生
伍孟涛,王海生,闫小宇,刘 彬, 葛芦生
安徽工业大学 电气与信息工程学院,安徽 马鞍山 243000
1 引 言
DC-DC变换器是目前应用最多的开关电源之一,可以将直流输入电压转变为直流输出电压[1]。在航天及军事领域中,为了能够在低成本、可靠性高的基础上,具有大容量、大功率的优点,并联电源技术就显得格外重要。因此研究开关电源的并联均流对于提高电源系统的稳定运行,具有一定的意义。
本文选用较为典型的BUCK变换器,研究其在并联状态下的动态性能、均流效果与鲁棒性。由于BUCK变换器属于强非线性系统,难以得到其准确的模型,且一旦受到外部干扰,将会让变换器产生非线性变化,传统的PI控制并不能满足实际需要[2]。1695年,Leibniz第一次提出关于微分阶次从整数阶推广到非整数阶,随后就有国外学者将整数阶的PID发展到分数阶领域[3]。FOPID与传统PID相比多了两个可以调节的指数,让参数的整定变得更加灵活,使得控制器的动态性能大幅提升,但是针对阶数改变引入的两个参数的整定和优化问题并没有提出一个有效的解决方案。文献[4]提出将预测函数控制(PFC)成功应用到机器人的控制上,很大程度解决了抗干扰能力差和稳态下的误差问题,却忽视了预测函数控制的动态响应较差,没有进一步研究与传统PID结合的控制策略。预测函数控制(PFC)属于MPC的一种,它与MPC相比的优点是鲁棒性强、在线计算量较低和跟踪能力强,另外,PFC的核心思想是注重控制输入的结构化[5],它将控制输入用基函数的线性组合代替,使整个控制过程的在线计算量大大减少。文献[6]在预测函数控制算法的目标函数中引入分数阶PI算法,二者结合得到了分数阶PI预测函数控制算法,并将其应用到逆变器中,通过仿真波形和实验波形表明逆变器的动态性能得到了提升,但是面对扰动,稳定性仍存在不足,但该算法与单一的控制算法相比,具有更好的控制效果。
将预测函数的成本函数与分数阶PID的增量表达式相结合,得到一个新的控制算法预测函数分数阶(FOPID-PFC)。文献[7]设计了将BUCK变换器和这种新型控制算法结合的控制策略,在一定程度上保留了分数阶PID控制良好的动态性能,也让预测函数控制的鲁棒性融合进来,使得控制系统的可靠性大大提升,但针对解决新得到的成本函数参数在线计算量大的问题,并没有提出一个有效的改进方法;文献[8]在总结这种新型控制策略的同时,引入了优化算法粒子群,通过粒子群在线整定成本函数参数,使得计算量大大降低,参数的选取也变得更加方便。上述两个关于这种新型算法的文献均只被用在单个BUCK电路中,在BUCK并联系统中没有得到应用和验证。
实现均流技术的控制方法尤为重要,如果盲目将各个模块进行并联,不仅会出现负载电流分布不均,而且还会影响系统的正常工作,甚至导致系统的损坏。结合一系列问题,本文在上述文献研究的基础上设计出基于主从均流的方式,通过v步离散法得到较为精确的分段仿射模型(PWA),并将这种新型控制算法预测函数分数阶,应用到并联BUCK变换器当中,不仅解决了电感电流分配问题,而且也大大提高了并联系统在面对负载扰动的情况下,整个BUCK变换器的输出性能和稳定性。
2 均流方法
对于并联系统,输出电感电流il的分配差异由各子模块的外特性不同造成。以一个简单的均流系统为例,外部特性不同分为两种:一是两个模块空载的电压不同,输出的负载阻抗相等;二是空载电压相同,输出的阻抗不同。
随着航天事业的发展,人们对并联系统存在的电流分配问题,正在保持积极的研究,解决方法也是层出不穷。输出阻抗法(下垂法)[9],并联的每个模块外特性呈下垂状,负载阻抗大,输出电压Vo小。在并联BUCK中,内阻小的模块输出电流较大,而内阻大的模块输出电流较小。此均流方法即将内阻小的模块外特性斜率调整至接近内阻大的模块,使得两个模块的电流分配较为均匀。文献[10]提出的平均电流自动均流法,即均流环参考电压为各个模块电流的平均值,但是当母线发生短路或者一些模块不能正常运行时,母线电压会下降,甚至会降到下限的阈值,导致DC-DC变换器故障的发生[11]。
本文选用主从并联方法,将一个模块作为系统的主模块,其余的为从模块。用主模块的电压控制其他并联模块的电压调整值,所有并联子模块均采用电流内环控制,将主模块的电感电流值i1作为从模块的电流环参考值iref,从而实现主从电流一致,得到很好的电流分配精度[12]。图1(a)为传统PI的并联BUCK结构图,图(1b)为预测函数分数阶的并联结构图。

(a) 双闭环PI控制
3 分数阶预测函数算法
3.1 分段仿射(PWA)
针对像DC-DC这种由非线性功率开关器件组成的模型,一般设计常见的线性模型控制器虽然比较简单,但是这些控制器在控制非线性模型对象时,很难准确地表现出变换器系统的运行状态。BUCK型DC-DC变换器属于切换线性系统,本小节提出利用其改进演变而来的分段仿射模型(PWA)[13]。先对BUCK变换器进行分段仿射建模,然后在此基础上提出分数阶预测函数控制算法,并且在分段仿射模型(PWA)下,对分数阶预测函数求得最优控制量。其中分段仿射系统原理图如图2所示。

图2 分段仿射系统原理图Fig.2 Schematic diagram of piece-wise affine system
分段仿射系统中含有多个连续变量的动态子系统,而且每个子系统中都含有一个附加常数项,这一点和其他切换系统是一致的,在图2可以看出,其子系统按照切换的策略在1到N之间进行切换[14]。虽然分段仿射的切换策略为离散状态,但是不同开关序列在同一个周期中1到N时处在连续的状态。
普通仿射系统定义如式(1)所示:
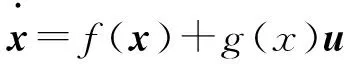
(1)
其中,x∈Rn为系统的状态变量,函数f:Rn→Rn与g:R→Rn×m为连续函数,u∈Rm为控制向量,并且f(0)=0。
对于同步整流的BUCK变换器,电感电流一直处于导通状态下,故本文只对CCM模式下的理想Buck变换器进行数学建模分析。其状态空间方程如式(2)、式(3)所示:
(2)
y(t)=Cx(t)
(3)
在一个开关周期内,不同的数学模型会根据控制器提供的不同PWM信号,使系统的状态变量发生改变,故如果能够找到PWM信号即d(k)与状态变量在不同开关周期的对应关系,即可建立Buck变换器的分析模型。本文利用v步离散方法[15],对BUCK变换器进行PWA建模,这里的v=3。

为了确定子区间类型,引入v个0和1变量并定义如下:
σn=1⟺d(k)≥n/ν,n=0,1,…,ν-1
(4)
式(4)为第n个子区间的状态:当σn和σn+1均为1时,子区间处于状态Q1;当σn为0时,子区间处于状态Q2;当σn为1,σn+1为0时,子区间处于Q1切换到Q2状态。故在第n个子区间按式(4)、式(5)所示进行状态更新:
Ξ3(ξ(n)):=Φξ(n)+Ψ1(v×d(k)-n)
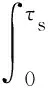

图3 子区间占空比信号变化示意图Fig.3 Schematic diagram of the change of the duty cycle signal of the sub-interval
最后得到PWA的BUCK变换器模型如式(5)所示:
(5)
其中:
A1=A2=A3=Φ3
B1=3Φ2Ψ1,B2=3ΦΨ1,B3=3Ψ1
f1=0,f2=Φ2Ψ1-ΦΨ1
f3=Φ2Ψ1+ΦΨ1-2Ψ1
则Buck变换器的PWA模型如式(6)所示:
x(k+1)=Anx(k)+Bnd(k)+fnn=1,2,3
(6)
3.2 分数阶预测函数
本文所设计的分数阶预测函数控制策略,是在预测函数的基础上加入增量式分数阶PID,其算法具体流程与预测函数大体一致,也包含基函数的选取、参考轨迹、预测模型、滚动优化以及误差的校正。
PFC算法的目的是使控制优化时域内的参考轨迹与预测值尽可能接近,故本文选取二次型性能指标函数的形式如式(7)所示:
(7)
其中,Qi,Ri为加权系数矩阵,P、H分别为预测时域及控制时域,yc(k+i|k)为k+i时刻的模型校正输出,Δu为从当前时刻起,M个连续控制增量。
PID的增量表达式如式(8)所示:
u(k)=u(k-1)+kpΔe(k)+kie(k)+kdΔ2e(k)
(8)
FOPID的增量表达式如式(9)所示:
Δu(k)=KpΔe(k)+
(9)
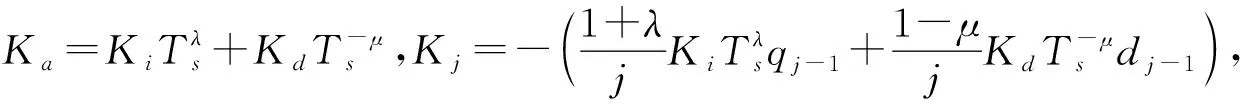
(10)
由式(7)的目标函数和式(10)的FOPID增量式得到本文设计的分数阶预测函数的新目标函数式(11):
(11)
其中,i是预测步长。为了找到最优控制量,使目标函数值最小,通过求极值得到控制量式(12):
(12)
其中,q-1为位移算子。
4 并联FOPIDPFC的仿真设计
本节将在Matlab/Simulink中搭建FOPIDPFC控制并联Buck变换器的仿真模型,通过仿真结果验证主从FOPIDPFC控制器设计的可行性。仿真中的主从Buck电路参数为Vin=12 V,C1=C2=210 μF、L1=L2=15 μH,Rmax=0.5 Ω,Rmin=0.25 Ω。此外,主从FOPIDPFC控制器参数相同,均为Ts=1×10-5s,Tr=6×10-5s,Kp=0.1,Ki=37.43,Kd=12.62,λ=26.86,μ=16.43,Q(2×2)=0.1×diag[1,1],h2×1=[2.04,2.37],R(2×2)=0.8×diag[1,1]。搭建的仿真模型如图4、图5所示。
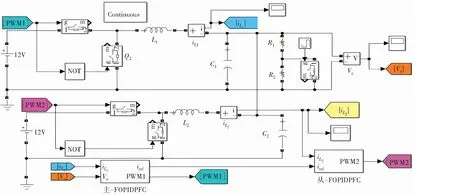
图4 主从FOPIDPFC控制并联Buck仿真模型Fig.4 Master-slave FOPIDPFC control parallel Buck simulation model

图5 主从FOPIDPFC控制器内部仿真模型Fig.5 Internal simulation model of master-slave FOPIDPFC controller
传统双闭环PI控制的电流参考值iref的取值与其电压外环紧密相关,输出电压的误差值会影响电压外环的输入。另外,电流内环的参考值由误差值经过电压外环调节得到。本文设计的分数阶预测函数与传统PI有所不同。在主从均流系统中,主FOPIDPFC控制器的输入并不仅与输出电压误差值有关,也与主变换器的电感电流值有一定联系,因此FOPIDPFC控制器电流值的选取准则不能和传统的PI控制一致。这里将第二节FOPIDPFC控制器的输出控制量表达式,计算简化,结合上面提到的双闭环PI控制的电流参考值选取原则,从显式中找出仅与输出电压差值相关的表达式,将其单独作为从FOPIDPFC控制器的电流参考值。得到的电流参考值iref的表达式如式(13)、式(14):
D=C(hi-Ai)A·[iL(k-1)vo(k-1)]T+
C(hi-Ai)B·u(k-1)-(hi-ai)·vo(k)+
(13)
iref=Q·S0·T1+Q·S1·T-Q·S2·T-1
(14)
式(14)中:T1表示的是开关周期延时一个周期D(1,1)的值,且D(1,1)为第一行第一列的值。M(1,2)、M(2,2)与其表达意思相同,即矩阵里的某行某列数值。
式(13)中:
L=[h1,h2,…,hp]TCm-
M=[h1,h2]TCmAmt-[CmAmt,CmAmt2]TAmt
S0=[K1·G1(1,2)+Ka·Gk(1,2)+Kp·ΔGk(1,2)]
S1=[Kp·ΔGk(1,1)-Kp·ΔGk(1,2)+Ka·Gk(1,1)]
S2=Kp·ΔGk(1,1)
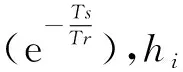
5 结果分析
图6为主从FOPIDPFC控制并联Buck变换器的仿真结果。从图6(a)中可以看出:主从FOPIDPFC控制的Buck变换器输出电压能够达到设定值2.5V,并且在加减载时,主从FOPIDPFC控制器能够快速地调节系统重新回到稳态值且具有较小的超调量。其中在加载时,系统经过70 μs的调节时间使得输出电压重新回到设定值,超调量为304 mV;在减载时,系统经过100 μs的调节时间使得输出电压回到设定值,超调量为450 mV。从图6(b)中可以看出:从Buck电感电流值与主Buck电感电流值始终保持相等,说明主从FOPIDPFC控制器的设计很好地实现了并联Buck变换器的均流效果。
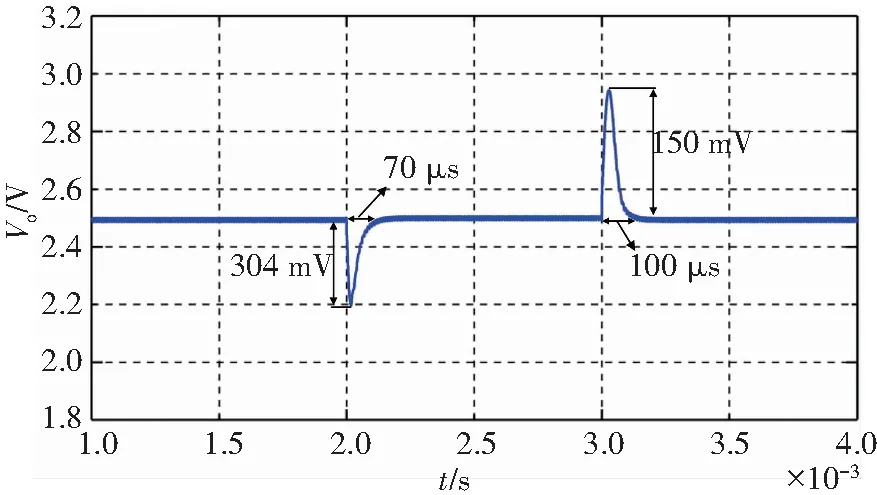
(a) 并联负载突变时输出电压波形
图7为传统双闭环PI控制的主从均流控制BUCK变换器的仿真结果波形。图7(a)中,负载在加载情况下,超调量为538 mv,调节时间为240 μs;系统减载时,超调量为671 mv,恢复时间为310 μs。

(a) 并联负载突变时输出电压波形
从仿真结果可以看出:分数阶预测函数控制的并联BUCK变换器在面对负载加、减载的情况下,超调量和调节时间分别降低了234 mv、170 μs和221 mv、210 μs。因此,采用本文的基于主从均流的并联方法分数阶预测函数控制在电流的分配精度、动态性能以及稳定性上均比传统双闭环PI控制更好。
6 总 结
在并联BUCK变换器的控制中,本文设计的分数阶预测控制策略,在负载受到加、减载的扰动下,其输出性能效果和动态响应均比PI控制优越,在电感电流分配上,也更加均匀。
由于本文引入的分数阶思想导致参数从原本的3个变为了5个,使得计算难度大大提高,未来可以在此基础上,对参数的整定和优化提出一种解决办法,降低计算量。
