Weibull分布下绕线联轴器双应力加速寿命试验研究

王海波， 白国振, 张志强

上海理工大学 机械工程学院，上海 200093

1 引 言

绕线联轴器作为一种常用的零部件，广泛应用于各种回转传动设备、传动设备与传动轴间的轴向连接，进行运动及扭矩的传递。对于正在工作的设备，若绕线联轴器工作时突然发生失效或在未监控状态条件下发生退化失效，都会给系统的维修以及保障带来巨大的影响，有时会造成巨大的经济损失。基于此，国内外学者对绕线联轴器寿命进行了不同程度的研究。

Dobre D等[1]对金属膜片联轴器进行了研究，采用有限元方法分析了轴向偏差和角度偏差对一个膜片单元的影响，为金属膜片联轴器的设计提供了思路；Loc Duong等[2]对航空领域的柔性膜片联轴器进行了研究，使用有限元分析来参数化应力特性，通过与旋转流体流动类比确定共轭应力集中，改进这些柔性隔膜的几何设计。Sekhar A S等[3]基于有限元分析方法，研究了联轴器安装过程中存在同轴度误差对系统振动问题的影响，模拟了同轴度误差所导致的谐波增加，得出弯曲模式的形状误差会对系统的振动产生很大的影响。魏政君等[4]研究了弹性联轴器的疲劳性能，以绕线式弹性联轴器为实验对象，进行了双轴扭转疲劳实验及疲劳前后的静态刚度实验，表明改进主轴方向的连接方案能满足大转矩疲劳实验要求。刘建武等[5]基于有限元分析方法对联轴器的固有频率与模态特性进行了研究，分析了膜片厚度联轴器固有频率和模态特性的影响，为动力传动轴和膜片联轴器的动态设计提供了理论参考。

目前国内外学者对联轴器展开一定的研究，但主要是采用有限元方法或利用疲劳寿命计算公式对联轴器寿命进行研究。同时针对特定对象绕线联轴器的研究相对较少，且未利用加速寿命理论与试验验证相结合的方法进行研究。因此，针对有限元分析方法存在的问题，利用加速寿命理论与试验验证相结合的方法对绕线联轴器的寿命进行研究。一方面证明了绕线联轴器的寿命服从威布尔分布，另一方面证明了本文所使用数据处理方法的有效性。

2 加速寿命试验方案的确定

2.1 绕线联轴器失效机理分析

绕线联轴器具有结构简单、稳定，其失效的原因主要包括：疲劳、磨损、损伤。绕线联轴器的失效形式与其工作环境密切相关，归纳起来主要包括下列几种失效形式[6]：

(1) 绕线联轴器中某部位因短时过载或疲劳强度不足而发生破坏；

(2) 绕线联轴器在工作过程中某部位产生过大的塑性变形或严重磨损；

(3) 绕线联轴器非正常工作条件下引起与其相连的其他零件失效；

(4) 传递性能下降。

2.2 加速应力与加速模型的确定

基于上文中对绕线联轴器的失效机理的分析，可知绕线联轴器的失效与环境应力几乎无关，仅与其工作时的工作应力相关。通过对绕线联轴器的实际工作条件进行分析，引起绕线联轴器失效主要包括两个应力，即：转速和所受的扭矩载荷，分别用S1和S2来表示。因此，选择绕线联轴器工作时的转速和扭矩作为其加速应力。

在加速寿命试验中，不同的产品适用于不同的加速模型。对于电子产品，加速退化速度与应力之间多数情况下满足Arrhenius模型；对于机械产品，加速退化速度与应力之间多数情况下满足逆幂律模型。王少萍等[7]论证了机械产品的加速模型确实服从逆幂律，提出了双应力加速逆幂律模型。因此，建立绕线联轴器的加速模型如下：

(1)

其中，ηij为绕线联轴器的寿命；Vi为绕线联轴器的转速；Pj为绕线联轴器承受的转矩；α、β为未知参数；η0为绕线联轴器的额定寿命；V0为绕线联轴器的额定转速；P0为绕线联轴器承受的额定转矩，且Vi、Pj相互独立。

对式(1)两边同时取对数，得到其线性表达式如下：

(2)

2.3 加速寿命试验的实施

文中的每个加速应力都具有多个应力水平，进行简单的组合试验会大大提高试验成本，同时降低试验的效率。为提高试验效率、降低试验成本，本文中选用Escobar-Meeker(E-M)法进行加速寿命试验[8-10]，试验中各测试点的安排如图1所示。

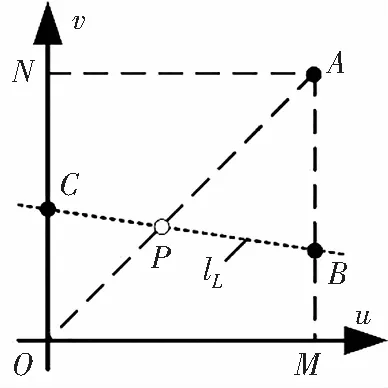
(a) 3个测试点

图1中实心黑点代表测试点，矩形区域 OMAN为组合测试点的可行域，直线lL和lM表示寿命-应力的关系，点P为直线lL与OA的交点，点K为直线lM与OA的交点，且K为线段PA的中点。对于可行域及其边界上的测试点，测试点上试验样本的数量与其到交点的距离成反比。根据有效试验原则，文中选择图1(c)的应力组合方案，得到加速寿命试验的条件矩阵如表1所示。

表1 加速寿命试验条件矩阵

基于上述试验条件矩阵在所搭建的绕线联轴器加速寿命试验平台上进行加速寿命试验，并对绕线联轴器工作时的相关数据进行实时采集并进行可视化处理。根据绕线联轴器的失效判断条件得到绕线联轴器的失效时间如表2所示。

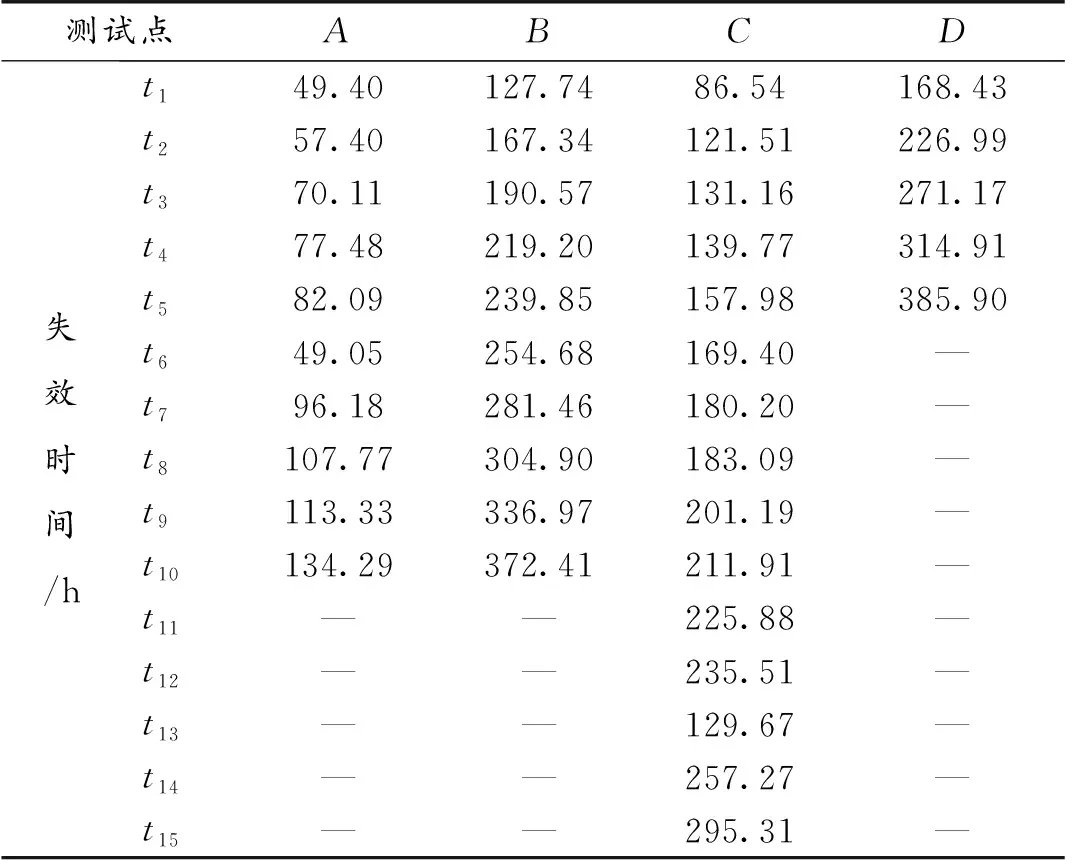
表2 绕线联轴器加速寿命试验失效数据Table 2 Accelerated life test failure data of winding couplings

3 试验数据的分析与处理

在对加速寿命试验数据进行分析处理时，主要包括两部分内容：加速寿命试验的基本假设与假设检验；参数的估计与正常工作条件下寿命特征的推算。

3.1 基本假设与假设检验

假设Ⅰ：在正常应力组合和加速应力组合条件下，绕线联轴器的寿命Tij都服从威布尔分布，其分布函数为

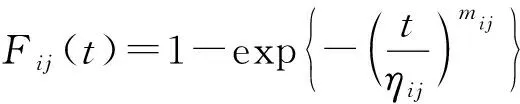
其中，i=0,1,…,k；j=0,1,…,l；mij为形状参数；ηij为特征寿命。

假设Ⅱ：在正常应力和加速应力组合条件下，绕线联轴器的失效机理保持不变，即：

m00≈mij=m

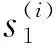
其中，β0、β1、β2、β3为待估参数；φ1(·)、φ2(·)、φ3(·)为已知函数，φ3(·)表示两个加速应力之间的相互作用。

根据上文的分析，绕线联轴器的加速模型服从逆幂律，绕线联轴器的两个加速应力之间无相互作用。故绕线联轴器的特征寿命与两个加速应力之间满足如下加速模型：

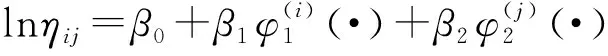
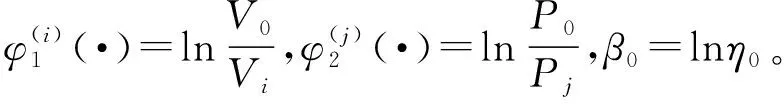
从威布尔分布的定义来看，绕线联轴器的寿命分布服从威布尔分布，但需要对其分布模型进行检验。检测产品的寿命是否满足威布尔分布的方法很多，本文中采用威布尔概率纸检验和巴特利特检验相结合的方式对绕线联轴器的寿命分布进行检验[11]。

根据中位秩计算公式对Fij(t)进行估计，对绕线联轴器的失效寿命数据进行描点，同时利用最小二乘法对数据点进行拟合配置直线，得到绕线联轴器的寿命数据分布如图2所示。

图2中，横坐标为绕线联轴器失效时间 对数lnt；纵坐标为威布尔分布函数Fij(t)的函数lnln[1/(1-Fij(t))]。以A测试点中绕线联轴器样本的失效数据为例，从图中可以看出，10个失效数据分布在一条直线两侧，其他测试点的失效数据亦是如此。同时图中的直线近似平行，且直线的斜率表示mij，即在各测试应力组合下的形状参数mij近似相等，满足假设Ⅱ。因此，可以初步判定绕线联轴器寿命分布近似服从威布尔分布。

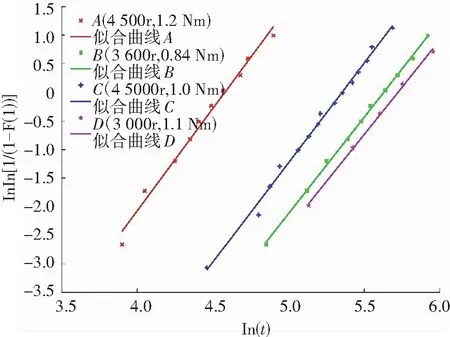
图2 绕线联轴器各组应力条件下的威布尔分布

为了进一步验证绕线联轴器的寿命分布为威布尔分布，采用巴特利特法验证各组测试点下的形状参数mij是否相等[12]。

检验假设：

H0∶m1=m2=…=mk

根据巴特利特统计量的构造，记：

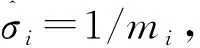
在试验中，设各组应力组合下有nij个绕线联轴器进行试验，截尾数为rij，本文中nij=rij，每个绕线联轴器样本的失效时间为

在加速寿命试验中，绕线联轴器的失效时间为一个随机数，可以采用不同的方法对试验数据进行分析，本文中主要使用下列两种数据分析方法对试验数据进行分析。

3.2 加速寿命试验的极大试验估计(MLE)

根据假设Ⅰ中绕线联轴器寿命Tij分布函数，其概率密度函数为

i=0,1,…,k;j=0,1,…,l

基于假设Ⅱ，可令mij=m；

基于假设Ⅲ得：

由此可得：

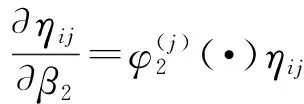
则参数β0、β1、β2、m的似然函数为

对数似然函数为

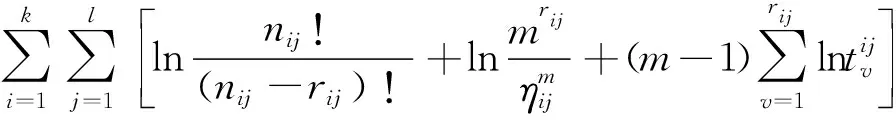
似然方程组为

基于似然函数方程组，可得如式(3)—式(5)三个表达式：

将式(3)—式(5)代入似然函数方程组中得：

利用Newtow-Raphson法求解是个超越方程组的到m、β0、β1、β2的估计值为

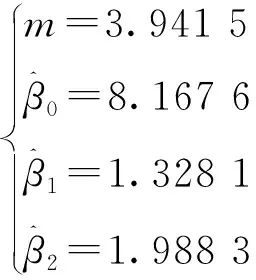
3.3 加速寿命试验的最佳线性无偏估计(BLUE)

上文中采用极大似然估计法进行参数的估计时比较复杂，对初始值要求较高，且很容易陷入局部最优解。因此，下文采用计算更为简单的BLUE对参数进行估计。

本文对绕线联轴器的失效寿命进行了分析，证明了其寿命Tij服从威布尔分布W(mij,ηij)，则绕线联轴器寿命的对数Xij=lnTij服从极值分布G(μij,σij)，其分布函数为

其中，μij=lnηij；σij=1/mij。

3.3.1模型中μij和σij的估计

根据表1加速寿命试验的条件矩阵可知，试验中测试样本的数量nij<25。则μij和σij的BLUE估计值为

其中，C(nij,rij,v)和D(nij,rij,v)为BLUE系数，可通过文献[13]得到。

根据绕线联轴器的失效数据，得到模型中参数的BLUE估计结果如表3所示。

表3 μij的σijBLUE估计值

3.3.2形状参数m的估计

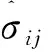
3.3.3加速模型中参数的估计

根据绕线联轴器的加速模型：

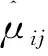
(6)

令ζij=Arij,nij，Arij,nij为方差系数，记

A=diag(ζ11,ζ12,…,ζ1l,…,ζij,…,ζkl)

由高斯-马尔可夫定理[13]，得到β的BLUE为

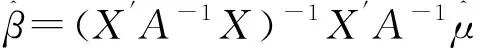
代入数据得到β的BLUE估计结果为

4 参数估计结果比较分析

采用两种参数估计方法对绕线联轴器分布模型中的参数进行了估计。极大似然估计法进行分布模型参数估计时相对比较复杂，具有对初始值要求较高，且容易陷入局部最优解等缺点；BLUE法相对简单，但对分布模型参数的估计结果精度需要进一步分析比较。因此，采用Akaike信息准则[14]将两种方法的参数估计结果进行比较。

Akaike信息准则的主要作用是衡量分布模型对绕线联轴器原始失效数据的拟合程度。fAIC值越小，则表示模型对原始数据的拟合程度越好，其定义如下：

fAIC=-2[ln(Lmax)-r]

(7)

其中，Lmax为似然函数的值，r模型中待估计参数的个数。

将上述两种参数估计方法与绕线联轴器的原始失效数据代入其似然函数中，得到AICMLE=308.67，AICBLUE=252.28。

从计算结果可以看出，BLUE的参数估计结果对原始失效数据拟合更好。同时结合图2中通过最小二乘法对各测试点失效数据拟合曲线斜率，进一步验证了BLUE法的参数估计结果优于MLE法的估计结果。

5 正常应力水平组合下的可靠性指标估计

绕线联轴器正常工作情况下，其额定转速及扭矩为V0=1 000r/min，P0=0.6 Nm。得到绕线联轴器的加速应力-寿命模型方程为

则绕线联轴器正常工作条件下的寿命η0=3 811.58 h。

平均寿命为

中位寿命为

根据参数估计结果，得到各测试点绕线联轴器的寿命及加速系数如表4所示。

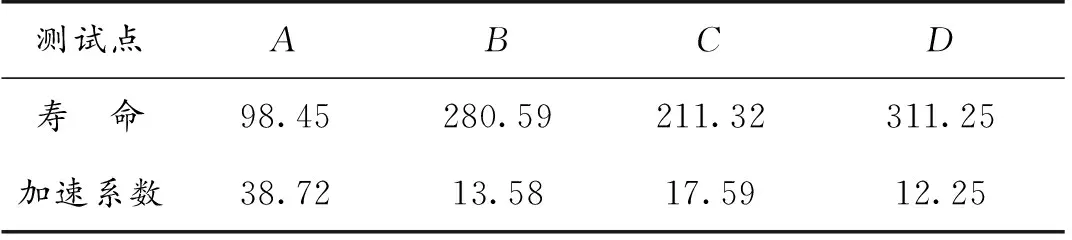
表4 加速应力下的寿命及加速系数

为了进一步验证绕线联轴器加速模型及其寿命分布是否合理。将加速寿命试验下绕线联轴器相关特征的计算结果与正常应力水平下的结果进行比较，如表5所示。

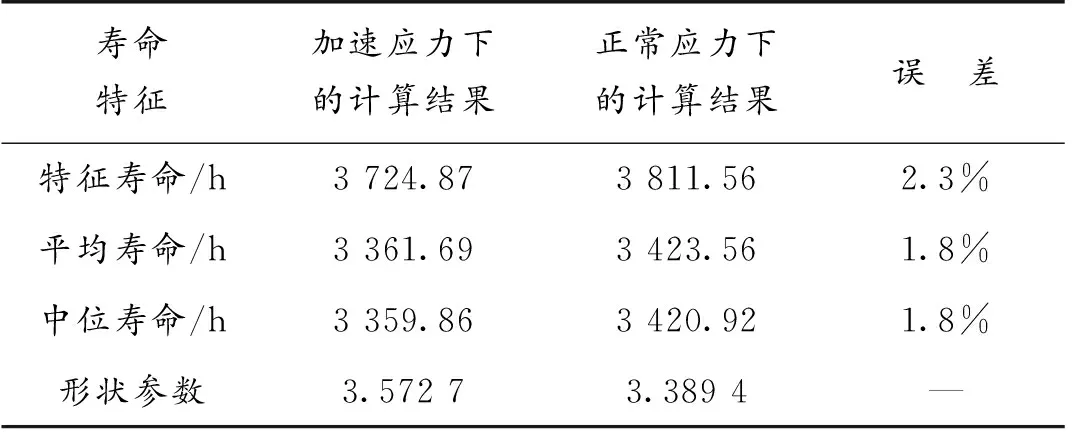
表5 加速应力与正常应力下的寿命特征比较

由表5可以看出，加速应力条件下与正常应力条件下获得的绕线联轴器寿命特征相差不大，相对误差在5%以内，证明本文中建立的绕线联轴器加速模型是正确的，进一步验证了本文中绕线联轴器加速寿命试验的可行性。

正常应力水平下绕线联轴器的可靠度函数为

R(t)=exp{-(t/3 811.58)3.389 4}

其可靠度曲线如图3所示。

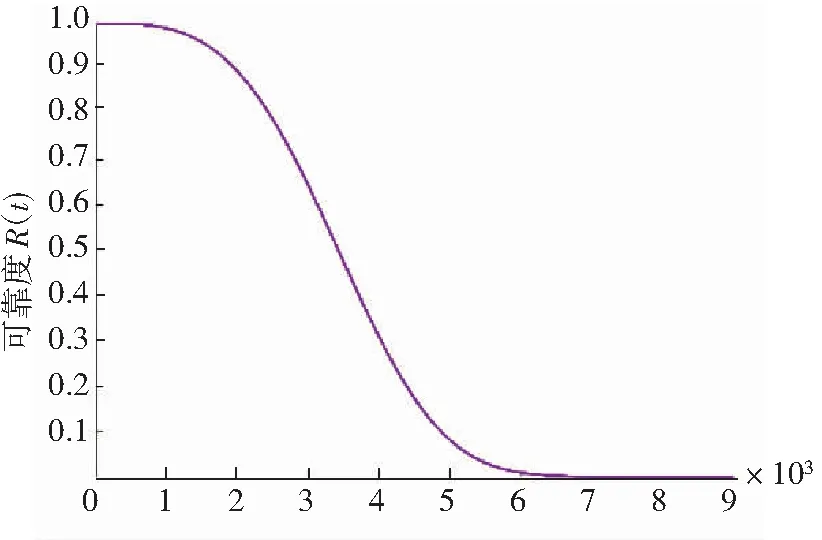
图3 正常应力水平下的可靠度曲线

6 结 论

采用恒加试验方法，建立了绕线联轴器双应力逆幂律-Weibull统计模型来对其寿命快速评估，利用极大似然估计法和最佳线性无偏估计法对绕线联轴器四组加速应力下的失效数据进行了统计分析，主要得出了以下结论：

(1) 绕线联轴器的寿命分布可以用威布尔分布精确描述，加速模型可以用逆幂律描述。

(2) BLUE可以更加精确地评估绕线联轴器加速模型中的参数。

(3) E-M法确保可以在短时间内估算正常应力下的寿命，测试时间和成本大大减少。