花瓣形燃料元件棒束通道内过冷流动沸腾特性数值研究

2023-02-21杜利鹏蒋泽平张文超侯延栋蔡伟华

原子能科学技术 2023年2期

杜利鹏，蒋泽平，崔军，张文超，侯延栋，蔡伟华,*

(1.东北电力大学热流科学与核工程实验室，吉林吉林 132012；2.东北电力大学能源与动力工程学院，吉林吉林 132012；3.中广核研究院有限公司，广东深圳 518031)

过冷流动沸腾是指在主流温度低于饱和温度情况下，发生在加热壁面附近的流动沸腾换热现象，该现象的发生极大增强了壁面的换热系数，因此，其广泛存在于核反应堆、电子散热系统等换热设备中。对于核反应堆，为提高核反应堆功率和获得更高的传热效率，高性能的燃料元件开发已成为重要手段之一。花瓣形燃料元件通过其自身螺旋结构使冷却剂搅混，换热性能增强，且无需定位格架，能够较大地提升核反应堆热工水力性能；与传统压水堆设计相比，在相同堆芯功率下，最大临界热流比提高58%[1]。因此，花瓣形燃料元件棒束通道内流动换热特性的研究，得到了国内外学者的广泛关注。

花瓣形燃料元件的螺旋结构会对流动产生重要影响。Shirvan和Kazimi[2]通过数值模拟方法对4×4花瓣形燃料元件棒束通道内的单相流动换热特性进行研究，分析了花瓣形燃料元件的结构及螺旋节距对通道内横向流动的影响。Xiao等[3]通过数值模拟，分析了通道内的横向流动分布，得到了横向搅混模型。蔡伟华等[4]研究发现，燃料元件螺旋产生的横向流动主要集中在燃料元件的内凹弧区域。同时，花瓣形燃料元件具有的螺旋结构，使其区别于传统的棒束通道内的换热特性。Fang等[5]对花瓣形燃料元件和非花瓣形燃料元件棒束通道内的高温氢气流动换热进行数值分析；从热工和水力综合性能来看，花瓣形燃料元件相较于十字非螺旋形和圆棒形元件分别提高了28%和6.1%。蔡伟华等[4]发现通道内产生的横向流动使得加热壁面温度呈不均匀分布，内凹弧的壁面温度明显大于外凸弧。Zeng等[6]发现入口流速和花瓣燃料元件的截面几何结构显著影响冷却剂换热特性。Shirvan[7]和Cong等[8]对花瓣形燃料元件的偏离核态沸腾(DNB)性能进行了数值研究，均发现蒸汽主要集中在燃料元件的内凹区域。此外，Cong等[8]发现，发生沸腾危机的位置不是相邻燃料棒间距最小时的截面位置。

在核反应堆高压高温运行工况下，通过实验来研究燃料元件棒束通道内冷却剂的过冷流动沸腾是极为困难的。随着计算流体力学(CFD)方法的高速发展，尤其是欧拉(Eulerian-Eulerian)两流体模型建立之后，进行燃料元件棒束通道内的两相流动数值模拟成为了可能。Krepper等[9]通过实验数据评估了欧拉两流体和RPI(Rensselaer Polytechnic Institute)壁面沸腾模型对过冷沸腾现象的预测潜力，发现大部分模拟工况下的计算值都与实验值符合较好，高压工况下预测偏差较大。Colombo等[10]通过20组实验数据评估了欧拉两流体模型对过冷沸腾预测能力，认为封闭模型限制了数值模拟的普适性。Pan等[11]验证了相间作用力模型对过冷沸腾的影响。Gu等[12]对适用于高压下的RPI壁面沸腾模型的封闭模型进行评估，并给出相对最优的模型组合。对于复杂通道内的过冷沸腾，Yang等13]和张蕊等[14]分别都使用RPI壁面沸腾模型，对具有定位格架和搅混翼的燃料棒束通道内的过冷沸腾现象进行了数值研究。

目前，针对花瓣形燃料元件棒束通道内冷却剂的流动与换热数值研究主要集中在单相流动与换热、横向搅混及偏离核态沸腾等方面。但花瓣形燃料元件棒束通道内的过冷流动沸腾特性的研究对核反应堆的安全设计具有重要的指导意义，而该方面的研究仍较为缺乏。因此，本文采用CFD方法，基于欧拉两流体模型和RPI壁面沸腾模型，对2×2花瓣形燃料元件棒束通道的过冷流动沸腾开展相关数值研究。

1 两相沸腾模型

过冷沸腾模型是基于欧拉两流体模型——将汽液流体均看成连续介质，汽液之间可以进行质量、能量、动量交换，交换量的大小在数学模型上体现在气液各相的质量、动量、能量方程的源项上。RPI壁面沸腾模型是在欧拉两流体模型的基础上，充分考虑了汽泡产生、生长及脱离现象对流动与换热的影响，建立的壁面沸腾模型，能较为准确地反映出过冷流动沸腾特性。

1.1 欧拉两流体模型

质量守恒方程：

(1)

式中，k、α、ρ、u、Δmk分别为气相v或液相l、相体积份额、密度(kg/m3)、速度(m/s)、两相之间质量传递(kg/(m3·s))。

动量守恒方程：

(2)

式中，p、g、Flv分别为压力(Pa)、重力加速度(m/s2)、相间作用力(N)。

汽泡脱离加热壁面后，进入主流区运动，会受到多种相间作用力的影响。相间作用力Flv包括曳力FD、升力FL、壁面润滑力FWL、湍流耗散力FTD。

Flv=FD+FL+FWL+FTD

(3)

汽泡和液体间的曳力FD为：

(4)

式中：Ai为相界面面积，m2；μl为液相黏度，kg/(m·s)；Re为汽泡雷诺数；dB为汽泡平均直径，m；CD为曳力系数，采用Ishii&Zuber[15]模型进行计算。

当连续相不均匀或旋转时，汽泡会受到垂直于速度方向的升力FL：

(5)

式中，CL为升力系数，采用Tomiyama[16]模型计算。

汽泡从壁面产生，壁面润滑力会使汽泡从壁面附近进入主流区域，壁面润滑力FWL模型如下：

(6)

式中：n为壁面方向矢量；CWL为壁面润滑力系数，采用Antal[17]给定的关系式计算。

由于主流区液相的湍流脉动产生湍流耗散力，使得汽泡从高浓度区向低浓度区运动。该力采用Lopez-de-Bertodano[18]模型进行计算。

(7)

式中：CTD为湍流耗散力系数，取值0.1；k为湍动能，m2/s2。

同时采用Sato[19]模型修正汽泡黏度，以此方法来考虑汽泡对液相湍流的影响。

能量守恒方程：

(8)

式中：h为比焓，J/kg；q为两相中的能量传递，W，由牛顿冷却公式计算：

q=hlAi(Tsat-Tl)

(9)

式中：hl为对流换热系数，W/(m2·K)，由Ranz Marshall[20]关系式计算；Tsat、Tl分别为饱和温度和液相温度，K。

1.2 RPI壁面沸腾模型

壁面沸腾模型通过对壁面热流密度分配来体现过冷沸腾中的传热现象，进而与汽泡的产生、生长、脱离等行为特性形成相互影响。由Kural和Podowski[21]提出的RPI壁面沸腾模型将壁面热流q″w分成3部分：单相热流密度q″c、淬火热流密度q″q及蒸发热流密度q″e:

q″w=q″c+q″q+q″e

(10)

q″c=hc(Tw-Tl)(1-Ab)

(11)

(12)

(13)

式中，hc、tw、Ab、f、λl、ddep、Nw、hlv分别为单相对流换热系数(W/(m2·K))、汽泡等待时间(s)、汽泡影响区域面积(m2)、汽泡脱离频率(1/s)、液相导热系数(W/(m·K))、汽泡脱离直径(m)、汽泡核化密度(m-2)、汽化潜热(J/kg)。

为使上述方程封闭，还需要参数——汽泡脱离直径ddep、汽泡脱离频率f、汽泡核化密度Nw及汽泡影响区域面积Ab的模型。上述参数计算关系式如下：

(14)

(15)

Nw=2101.085(Tw-Tsat)1.085

(16)

(17)

式中：a、b、φ可参考文献[22]；Ja为过冷度雅克布数。

2 模型验证

采用Bartolemei[23]的均匀加热圆管高压实验及相关实验数据进行模型验证。几何模型如图1a所示，实验工况如下：热流密度为570 kW/m2、压力为4.5 MPa、质量流速为900 kg/(m2·s)。模拟采用Standardk-ω结合增强壁面函数。通过对比实验与模拟得到的轴向壁面温度、流体温度及空泡份额分布情况，分析二者误差大小，验证模型可靠性。图1b为模拟获得的结果与实验数据对比，并通过式(18)计算相应的壁面温度、流体温度及空泡份额的均方根误差，计算结果分别为1.61 K、2.07 K、0.044。可知，模拟结果和实验数据吻合良好。

(18)

a——Bartolemei实验几何模型；b——计算值与实验值对比图1 模型验证Fig.1 Model validation

3 几何模型及网格划分

3.1 几何模型

为研究花瓣形燃料元件对棒束通道内过冷沸腾的流动和传热特性影响，本文选取2×2花瓣形燃料元件棒束通道为研究对象，其几何结构形式如图2～4所示。具体结构参数列于表1。实际应用中，在燃料元件旋转了1/4的螺距处，燃料棒之间通过4个接触点支撑；而网格划分中，支撑点处网格难以划分，所以在燃料元件间增加一定的距离。蔡伟华等[4]分析了不同距离对冷却剂传热的影响，发现距离d为0.5 mm时，子通道内流体温度相对偏差小于0.1%，所以本文采用上述参数建立模型。

图2 花瓣形燃料元件Fig.2 Petal-shape fuel element

图3 流体域Fig.3 Fluid domain

图4 燃料元件排列方式Fig.4 Fuel element arrangement

3.2 网格划分及边界条件

使用ICEM软件对2×2花瓣形燃料元件棒束通道进行结构化网格划分。将整个流体域划分成含燃料元件的内流体域和方形壁面的外流体域，中间通过interface面进行两部分的插值计算。具体网格如图5所示。入口和出口分别设置为速度进口和压力出口，燃料元件壁面定义为无滑移壁面，采用均匀热流条件，方形外壁面设置为周期性边界条件。表2中列出了数值模拟工况具体参数(具体值参考压水堆可能出现的运行工况)。

表1 几何参数Table 1 Geometric parameter

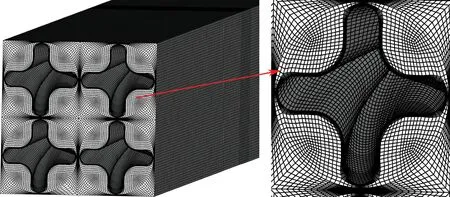
图5 计算域网格Fig.5 Calculation domain grid

表2 模拟工况Table 2 Simulation of working condition

3.3 湍流模型及网格无关性验证

湍流模型在流动换热模拟中起着至关重要的作用。压水堆燃料组件通道内，由于组件产生旋流和近壁湍流各向异性导致通道内形成次级涡流，优先考虑选择SSTk-ω、RNGk-ε、RSM湍流模型。如Liu等[24]对典型压水堆燃料组件通道内的流动进行数值模拟，评估了各种湍流模型，发现SSTk-ω湍流模型对近壁面的处理性能更优。对于花瓣形燃料元件棒束通道，因其螺旋结构产生了复杂流动，蔡伟华等[4]和Fang等[5]对花瓣形燃料组件通道内单相流动评估了不同湍流模型的影响，根据相关实验数据表明，SSTk-ω模型能获得更好的结果。所以本文湍流模型选择SSTk-ω模型。

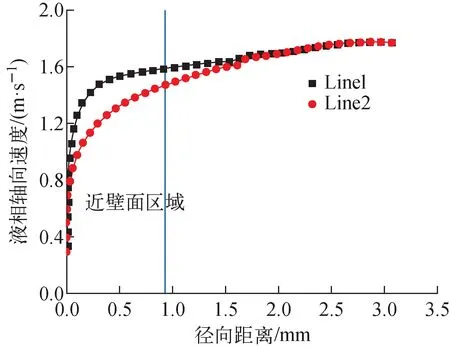
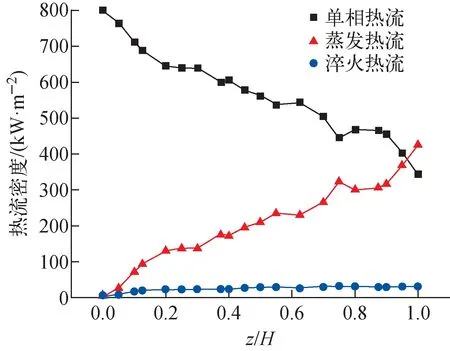
根据上述模型设置，对研究对象进行网格无关性验证。Fluent对SSTk-ω模型引入增强壁面函数，使得该模型对近壁面网格精度要求降低，允许1

图6 网格无关性验证Fig.6 Grid independent validation

4 结果与讨论

4.1 流动特性分析

图7为轴向不同截面的液相流动速度分布。由图7可看出，冷却剂以1.4 m/s的均匀速度进入通道内后，受到花瓣形燃料元件的螺旋导向作用，流场迅速发生变化，中心区域的速度最大达到2 m/s；燃料元件的内凹弧壁面附近，冷却剂的速度低于截面平均速度，最低值为1.05 m/s；外凸弧处因其周向角度变化更大，使得流动阻力较小，近壁面附近的流体速度比内凹弧处的流速大，二者最大相差0.6 m/s。在内凹弧区域内，由于流体围绕燃料元件流动，使得流场的分布特点也逐渐随顺时针方向旋转，呈现不均匀性分布。花瓣形燃料元件和绕丝型燃料元件具有一定相似性，根据Song等[26]对绕丝型燃料元件的研究可知，在花瓣形燃料元件凸弧与主流相遇的一侧称为迎风侧，对侧为背风侧。由于流动阻力，使得迎风侧的压力变得高于背风侧的压力，如图8所示。结合图7可看出，在外凸弧的两侧壁面附近，流速呈现非对称分布，迎风侧附近速度与主流速度更接近，背风侧附近速度存在一定的梯度。

图7 工况4轴向液相流动速度分布Fig.7 Axial liquid phase flow velocity distribution of case 4

红色高，蓝色低图8 截面局部压力分布Fig.8 Cross-sectional local pressure distribution

图9 沿直线Line1和Line2液相流动速度Fig.9 Liquid phase flow velocity along Line1 and Line2

为量化分析凸弧两侧的流场不均匀性，同时鉴于燃料元件的对称性，在内凹弧区域的迎风侧(Line1)和背风侧(Line2)取两条直线，如图7所示。图9为直线Line1和Line2上液相流动速度变化情况。可看出，在近壁面附近，Line1处的液相速度梯度变化大于Line2处，且在一定距离内，Line2处的速度低于Line1处，此结果势必使得Line1处的流动换热强于Line2处。图10为不同入口流速下，Line2处的液相流动速度随径向距离的变化趋势。由图10可知，入口流动速度从1.4 m/s增大到2.5 m/s过程中，直线上的局部流动速度达到截面平均速度的径向距离逐渐增大，由此可知，入口流速增大，将增加内凹区域的流场不均匀性程度。

图10 不同入口流速下Line2位置处液相流动速度Fig.10 Liquid phase flow velocity at Line2 position at different inlet flow velocities

图11为工况3中不同轴向位置处，液相横向流动速度分布。从图11可见，横向流动主要集中在花瓣形燃料元件的内凹区域，横向流动方向与燃料元件扭转方向一致，迎风侧横向速度大于背风侧速度，其原因为在迎风侧，主流流体与迎风侧壁面相遇产生逆流，增大横向流动速度，使得内凹弧区域横向速度分布不均匀，最大值为0.045 m/s。从燃料元件相对入口位置旋转了90°的位置处(z/H=0.25)起，通道的中间位置逐渐形成一个相对速度较小、与横向流动方向相反的涡旋，使燃料元件内凹处与中间区域的流体搅混，起到强化换热的效果。

图11 工况3中不同轴向位置的液相横向流动速度分布Fig.11 Liquid phase transverse flow velocity distribution at different axial positions in case 3

为体现花瓣形燃料元件产生的横向流动能力，定义平均横向流动强度F，定义如下：

(19)

式中:Vx、Vy、Vz分别为横向速度分量和轴向速度，m/s；A、Ai分别为截面面积和网格面积，m2。

图12为不同入口流速下横向流动强度沿轴向变化曲线。花瓣形燃料元件由相对角度0°增到45°的过程是棒间隙增大的过程，之后相对角度由45°增到90°的过程是棒间隙减小的过程，因此燃料元件每1/4的螺距变化会形成1个变化周期。从图12可看出，流体在经过充分发展后，横向流动强度沿轴向呈波动变化，且其变化趋势与花瓣形燃料元件棒束的间距周期变化一致，在间距增大时横向流动强度减小，反之增大；由不同入口流速的模拟数据分析，入口流速从1.4 m/s增到2.0 m/s，横向流动强度仅小幅增加，而在速度为2.0 m/s和2.5 m/s下，横向强度变化基本一致，表明入口流动速度对横向流动强度的影响基本可以忽略。

图12 不同入口速度下横向流动强度Fig.12 Transverse flow strength at different inlet flow velocities

图13为不同热流密度下横向流动强度沿轴向变化趋势。热流密度为450 kW/m2时，通道刚发生过冷沸腾，随热流密度的增加，过冷沸腾程度增强，3个不同工况下的液相横向流动强度变化趋于一致，表明气相的产生和过冷沸腾的剧烈程度并不会对横向流动产生影响，同时可注意到，气相横向流动强度大于液相横向流动强度，这是由于气相从壁面进入主流区时，除了受到花瓣形燃料元件的作用，还受到湍流耗散力和壁面润滑力的影响。对于热流密度600 kW/m2工况中的气相横向流动强度大于800 kW/m2工况，由式(4)、(5)可知，曳力与汽-液界面面积呈正比，升力大小与空泡份额呈正比，因此，热流密度增大时，空泡份额和汽泡尺寸都在增加，曳力和升力同时增大，当汽液之间的曳力与升力的作用大于湍流耗散力等横向力的作用时，气相的横向流动被削弱。

图13 不同热流密度下气液两相横向流动强度Fig.13 Transverse flow intensity of gas-liquid two-phase at different heat fluxes

4.2 空泡份额分布特性

图14为工况4中轴向不同位置处的空泡份额分布。由图14可知，在z/H=0.375截面处，过冷沸腾最先在内凹弧区域内发生。这是由于在内凹弧区域处，流体的换热面积更大，产生的热量最多，且内凹区域处的流动速度更小，因此，壁面附近的流体更易达到饱和温度，进而发生过冷沸腾。z/H=0.5位置后，发生过冷沸腾的区域增加，流体在花瓣形燃料元件的导向作用下，使得气相扩散到不同子通道，且受中间通道内的旋流影响，在通道内形成相对均匀的分布；至通道出口位置处，内凹区域空泡份额最大为0.11，而外凸弧区域空泡份额为0.04，花瓣形燃料元件的内凹弧处的空泡份额仍大于其他位置。

图14 工况4中不同轴向位置空泡份额分布Fig.14 Distribution of void fraction at different axial positions in case 4

图15示出了燃料元件不同轴向位置处空泡份额沿周向的详细分布。处于不同截面位置时，图15a对燃料元件周向方向作出定义，其角度和图15b、c相对应。由图15b、c可知，z/H=0.5截面内凹区域内，空泡分额呈非对称分布，燃料元件的背风侧方向(15°、110°、195°、285°)附近的空泡份额大于其在外凸弧对应的迎风侧处(70°、160°、250°、340°)的空泡份额，且在燃料元件相对z/H=0.5位置扭转45°(z/H=0.875)后，上述现象依然存在，结合图11的z/H=0.5截面横向流速分布可知，在花瓣形燃料元件内凹区域中，横向流速大的位置，其空泡份额小，反之亦然。造成这种现象的原因是较大的横向流速，增强了冷热流体搅混能力，导致过冷沸腾减弱，空泡份额相对较小。通过不同工况中空泡份额分布可知，在一定热流密度下，对于壁面附近的过冷沸腾程度，内凹弧区域始终大于外凸弧区域。因此，对于压水堆工况下，更应关注花瓣形燃料元件内凹弧区域的热工水力特性。

a——周向角度定义；b——横面z/H=0.5空泡份额；c——截面z/H=0.875空泡份额图15 空泡份额沿周向的详细分布Fig.15 Detailed distribution of void fraction along circumferential direction

4.3 换热特性研究

图16为工况4的不同轴向位置处，花瓣形燃料元件的壁面温度沿周向分布情况。由图16可知，燃料元件内凹弧区域的壁面温度分布均匀，沿主流方向，在该区域内的过冷沸腾程度逐渐增加，壁面温度整体呈下降趋势；在燃料元件的外凸弧区域，存在剧烈的壁面温度变化，结合图7和图14可知，z/H=0.25位置处，壁面与流体处于单相对流换热阶段，外凸弧壁面附近液体流动速度相对较大，换热效果更好，因此，壁面温度相较于内凹弧壁面显著更低。在z/H=0.25截面后，外凸弧壁面温度快速上升，在接近出口位置时，外凸弧壁面温度大于内凹弧壁温，外凸弧两侧的壁面温度出现峰值。通过图17中z/H=0.75和z/H=1位置处的单相热流密度分布可看出，内凹弧和外凸弧交接处的单相热流密度也存在峰值，分析其原因，主要是由于随主流温度的升高，单相对流换热能力逐渐减弱，虽然该位置处存在单相对流换热的峰值，但相变所需的汽化潜热不足以抵消单相对流换热的减弱，导致壁面温度较高。

图16 工况4中壁面温度周向分布Fig.16 Circumferential distribution of wall surface temperature in case 4

图17 单相热流密度周向分布Fig.17 Circumferential distribution of single-phase heat flux

图18为工况6单相热流密度、淬火热流密度、蒸发热流密度沿轴向变化。其中蒸发热流密度为在气泡生长过程中，由于从液体到蒸汽的相变而发生的热传递，淬火热流密度是对气泡脱离处的壁面与冷流体接触时的热传导的量化值。在入口段，由于流体过冷度高，主要发生单相对流换热，随壁面温度的增加，壁面上成核点增加，汽泡脱离壁面，蒸发热流密度和淬火热流密度都获得增加，相应的单相热流密度下降，但可看到其并未呈现线性的快速下降趋势，还出现小幅上升，其原因是花瓣形燃料元件的螺旋结构加大了流体的搅混作用，使得单相热流密度增强。同时可注意到，蒸发热流密度快速增长，而淬火热流密度维持在较低增长。根据Hsu[27]提出的核化理论，要使汽泡生长，汽泡顶部的液体温度要达到所需的过热度，因此对于附着在加热壁上的小汽泡，需要一定的过热层，使汽泡不断变大后脱离。结合图11可知，主要发生过冷沸腾的内凹区域内存在持续的横向流动，使得加热壁面上过热层较薄，当汽泡的顶部到达过冷区域时，汽泡开始坍塌。大量汽泡生长，使得蒸发热流密度在出口处达到最大，而汽泡脱离频率低，淬火热流增长慢。