永磁电机齿槽转矩的谐波分析

2023-02-21吴昊

现代制造技术与装备 2023年1期

吴昊

（海军装备部，北京 100080）

永磁电机结构简单、效率高，在电动汽车、电动装甲车及电动传送装置中应用普遍。然而，受限于自身机构，永磁电机存在转矩波动问题，目前普遍使用斜槽进行优化。斜槽能降低电阻的变化而减少齿槽转矩，但电机结构复杂。本文计算并分析齿槽转矩的谐波情况后，尝试利用谐波完成对电机的优化[1]。

1 电机模型

构建的电机模型忽视了铁心饱和、涡流以及磁滞造成的影响，且将电流视作正向的三相正弦波。此时，在d-q轴模型中，电磁扭矩为

式中：p为极对数；λ为气隙定子磁链幅值；iq为交轴电流；id为直轴电流；Lq为交轴电感；Ld为直轴电感。表贴式电机中，永磁磁链与交轴电流作用产生电磁扭矩。内置型电机中，转子同样影响电磁扭矩。因此，在理想状态下，式（1）能够维持扭矩的稳定性。在定子的齿槽和电机磁极边界的影响下，产生齿槽扭矩并发生对应变化。针对扭矩的变化情况，采用有限元计算方法能便捷地完成分析和后续计算。

根据设计要求，表贴式和内置型设计的额定转速均为3 000 r·min-1，转矩为33 N·m。这两种电机定子的参数均为外径180 mm、内径91 mm，电机为3相24槽，单槽的槽口部分宽度为3 mm，铁心300 mm，气隙1 mm，转子的外径部分为90 mm，且极对数均为2。表贴式和内置型电极的主要区别在于磁极厚度和极弧系数不同。

在槽距的影响下，电机的齿槽扭矩呈周期性变化。为便于计算，电机角度设定为360°。

2 谐波分析

根据对齿槽扭矩的定义，设Wgap为气隙的磁场储能，α为转子角度的导数，则有

电机中定子和电子的磁导率较大，因此式（2）可以近W似等同于式（3），即

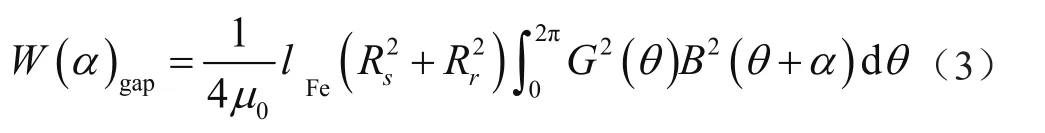
式中：lFe为铁心的长度；Rs为定子内径；Rr为转子外径；G(θ)为气隙的有效磁导；B(θ)为气隙磁密的分布函数。

利用傅里叶函数可将式（3）化简为

式中：Ns为定子槽数；Np为极对数。

将式（3）和式（4）代入式（2），有

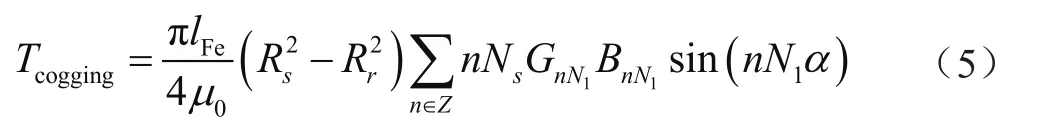
式中：N1为Ns、Np的最小公倍数。

2.1 谐波分量和极弧系数的优化分析

对永磁电机相邻的磁极边端和定子的铁心而言，两者之间的互相作用力为

式中：ai、bi为傅里叶系数；γs为槽距；x为磁极的位移；t为极距和磁极的宽度差。

电机中，齿槽力主要体现在二次谐波的形成方面，因此有

调整磁极的宽度后，有

满足式（8）时，电机的齿槽力能降至最低。当二次谐波中高次谐波的数量增多时，则超过式（8）的使用范围。

内置型和表贴式2种类型的永磁电机，根据最优状态计算得到的极弧系数极为相似，计算结果分别为0.82和0.83。采用上述优化方法能够满足优化需求，将扭矩控制在额定2%左右。

2.2 定子齿槽的优化及分析

2.2.1 槽口宽度

由式（3）可知，作为长度系数的G(θ)，其变化会对展开后的系数Gn产生影响。使用有限元计算模式优化前，谐波的统计情况如图1所示。当电机的槽口宽度控制在1～3 mm时，这一阶段电机的扭矩基本与槽口的宽度变化呈线性关联。

2.2.2 槽数影响

以图1的2种电机作为案例，2种电机模型均包括24个定子，定子的铁芯共计24个。这一模型体系定子与磁极对应的情况下，每一个磁极对应6个定子，呈现整数分布状态。在不考虑机械影响和电机永磁体差异造成影响的情况下，每个磁极对应的齿槽数量均相同，最终结果为4个磁极的叠加，不利于降低扭矩。

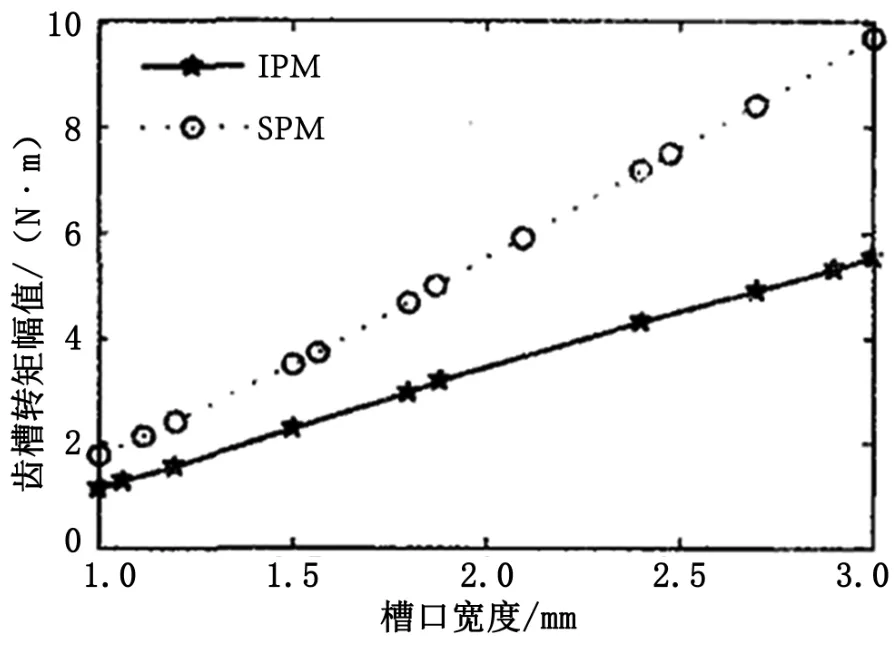
图1 槽口宽度变化

任何类型的电机在计算槽距角时均应根据机械角度进行计算，计算式为2π/Ns，磁极的铁心数量计算式则为Ns/2Np。当磁极相应的槽数为非整数时，计算每个磁极对应槽数的余数时可以采用计算式m/2Np，且该种情况下磁极与铁心齿产生的扭矩为cogβ。齿槽扭矩的计算公式为

式中：β0代表第一块磁极在初始状态下的位置[2]。磁极偏转角，如图2所示。通过调整Ns和Np可以调整扭矩产生的象限。通过式（9）进行调整时，同样能够根据电机产生的一次谐波或多次特定谐波进行调整，以减少电机产生的齿槽扭矩。另外，若电机实际的磁极数量相对较多，可通过对1对极和2对极象限的调整完成调节，调节同样参考式（9）[3]。