一类常微分方程的解法研究与推广

史周晰 赵临龙

安康学院数学与统计学院 陕西安康 725000

1 问题背景

微分方程是伴随着微积分创立而诞生的，牛顿在建立微积分的同时，对简单的微分方程用级数来求解。后来数学家欧拉、克雷洛、达朗贝尔、拉格朗日等人又不断地研究和丰富了微分方程的理论。

微分方程的起源可追溯到17世纪末，为了解决物理问题、天文学问题，出现了微分方程。数学家曾借助于微分方程从理论上得到了行星运动规律，从而验证了德国天文学家开普勒由实验而得到的推想。后来，法国天文学家勒维烈和英国天文学家亚当斯也曾借助微分方程，在海王星被观测到之前推算出它的方位。微分方程成为研究自然规律的强有力的工具。

同时，随着今天数学建模的兴起，微分方程解决实际问题的作用更加凸显出来。1798年，马尔萨斯人口增长模型成为利用微分方程研究社会问题的先例。尽管马尔萨斯人口增长模型较粗糙地研究人口增长(较实际增长过快)，但推动了数学建模的兴起，使常微分方程成为研究自然科学和社会科学中的有利工具。

2 解法研究

在《常微分方程》学习检测中，对于一阶微分方程

(xy+1)ydx-xdy=0

(1)

如何求其解，是非常有趣的问题。

通过初等变换，将微分方程(1)化为可以求的微分方程。

2.1 解法1：积分因子公式法

2.2 解法2：积分因子观察法

2.3 解法3：化为变量可分离方程求解

(2)

(3)

2.4 解法4：化为伯努利方程求解

2.5 解法5：一阶线性方程解法

2.6 解法6：常数变易法

(4)

(5)

由此猜想，方程的解的形式为y=xc(x)

xc′(x)+c(x)=c(x)+x2c2(x)

3 推广探析

将微分方程(2)推广为：

(6)

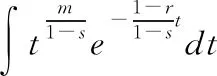
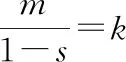
代回z=y1-r，t=x1-s

4 解法小结

对于微分方程的解法研究，是一个有趣的问题。首先，它不仅能给出问题的求解，而且还可以将结论进行推广，获得新的结果，丰富微分方程的理论。更重要的是，通过一题多解给出不同的解法，培养了学生的发散思维，提升解决微分方程的能力。

我们在微分方程学习与研究中，一直提倡“学习+研究”的方法，引导学生发表一系列论文[1-28]，不仅提高学生学习微分方程的积极性，而且成为参考文献[29]的补充内容，以及参考文献[30]展示的亮点。

5 成果亮点

学生能力得到极大提升，发表微分方程论文60余篇(核心期刊2篇)，考取的60名硕士研究生多数发表论文，成为考研的亮点。

在实践活动中，针对大学生承担的国家、省级等创新项目(共12项)完成的微分方程模型论文发表在核心期刊中，将微分方程融入竞赛答题中，在国际和全国数学建模竞赛获得奖项60余项、陕西省“挑战杯”竞赛奖9项，成为学校学风建设的试点学院。

本课程先后被学校评为精品课、示范课、混合改革课等，课程考试改革评为优秀等次；2016年《常微分方程》确定为学校考试改革课程；2017年确立为校级教学示范课程建设项目；2017年确立为校级混合改革课程；2017年《基于常微分方程课程的“学习+研究”教学模式的构建与实践》获得学校教学成果一等奖；2018年该成果入选2018年全国大学数学课程论坛论(论文集：高等教育出版社)；2019年该成果在全国“新工科背景下大学数学及教材建设研讨会”报告，并到相关高校做交流报告。2019年《兴趣驱动、案例融入、学研结合的常微分方程课程教学改革与实践》获得学校教学成果特等奖。2020年《常微分方程》成为省级一流课程。

2001年，辅助教材《常微分方程研究新论》[30]凭借丰富的教学研究成果获得陕西省教学成果二等奖。同时，以专题讲授的方式，通过学习群传递老师的发表论文，引导学生开展学习研究，提升学习和研究能力。

2014年，教材《常微分方程》[29]第三次印刷，教学改革促进教师发展：2名青年教师晋升副教授，教授成为陕西省级特支人才(教学名师)。