水环境治理PPP项目可持续供应商选择研究

汪伦焰，李 颖，安晓伟，梁梦轩

（1.华北水利水电大学 水利学院，河南 郑州 450046；2.河南水谷创新科技研究院有限公司，河南 郑州 450000）

1 引 言

在环境治理领域运用PPP模式，充分发挥社会资本在融资、建设、技术、运营等方面的优势，可以缓解政府的财政压力，促进环境治理效率和环境服务水平的提高。根据财政部PPP项目库数据，我国现有PPP项目10 244个，其中水环境治理PPP项目占9.4%。水环境治理PPP项目在一定程度上影响着国家和地区的经济、社会和环境可持续发展，因此提高水环境治理PPP项目的可持续发展水平，促进水环境治理PPP项目的成功运作意义重大。PPP项目中社会资本方的选择对项目建设、运维、移交等有很大影响，是水环境治理PPP项目成功的前提条件。为了促进水环境治理PPP项目和公共采购的可持续发展，选择具备可持续性的供应商至关重要。

目前关于PPP项目社会资本方的选择已经有了较为深入的研究，包括社会资本方选择评价、决策方法等。选择评价方面，现有研究大多基于三重底线理论构建可持续供应商选择指标体系［1－3］。PPP项目具有复杂性，Hatush等［4］认为评价社会资本方不能只考量价格因素，必须对社会资本方财务、技术、管理等能力进行全面分析。刘秋常等［5］在分析周口市水环境治理项目特点的基础上构建了以财务实力、技术能力、管理能力、类似经验和声誉为准则层的PPP项目私营部门合作伙伴综合评价指标体系。易欣［6］从社会资本的履约能力、管理能力、信用表现和项目表现出发，构建了PPP轨道交通项目社会资本优选综合评价指标体系。Zhang等［7］确定了包含基本能力、管理能力、历史业绩和信用绩效、项目绩效和可持续发展的PPP项目私人合作伙伴的选择标准。决策方法方面，现有研究提出了多种决策方法，如可能性分布－犹豫模糊语言集［1］、复杂比例评估－逐步权重评估比率分析［2］、区间二元语义混合加权距离测度－失效模式与后果分析模型［3］、IAHP－Vague集理想解［6］、直觉模糊层次分析法［8］、区间值直觉模糊集TOPSIS法［9］、多目标群决策迭代算法［10］、区间二元语义VIKOR［11］等。现有研究构建的社会资本方选择评价指标体系大多没有考量指标的可测量性，且对社会资本方可持续能力考量不足；在评价指标体系分析过程中很少关注指标的动态变化及其相互间的影响；很少有研究考虑群决策过程中决策者对模糊信息的偏好程度以及决策者的权重，决策结果可靠性不强。水环境治理PPP项目与其他行业PPP项目既有共性，也有其自身独特性，水环境治理项目更强化综合治理观念，还有长期可持续发展的实际需求，但目前针对水环境治理PPP项目可持续供应商选择的研究较少。

针对上述问题，从可持续公共采购角度，结合水环境治理PPP项目特点，构建水环境治理PPP项目可持续供应商选择评价指标体系，提出基于概率犹豫模糊集和全乘比例多目标优化（MULTIMOORA）方法的可持续供应商选择决策模型。概率犹豫模糊集通过概率大小描述每个犹豫值重要性差异程度，刻画专家对每个犹豫值的偏好程度，以便获得更加全面合理的决策信息［12］。因此，运用概率犹豫模糊集刻画决策专家的评估信息，引入Shapley值确定决策者权重，该方法考虑了专家认知的局限性和专业的差异性，增加了决策过程的合理性。Maclaurin对称平均算子（MSM）在解决属性独立的多属性决策问题时具有灵活有效性，可以描述多参数之间的关系。将Maclaurin对称平均算子与基于阿基米德（Archimedean）范数的概率犹豫模糊有序加权算子相结合，不仅考虑了属性间的关系，而且可以更好体现单个属性的重要性。Brauers等［13］提出的MULTIMOORA方法是采用比率法、全乘模型、参照点法对方案进行比较和选择，使得结果更加合理。MULTIMOORA方法是迄今为止最稳健的多目标优化方法，其简单、有效、便捷，有广泛的应用场景［14］。将概率犹豫模糊集与MULTIMOORA法相结合，在考虑决策者偏好的基础上，多角度对参与投标的供应商进行比选排序，以提升模型的可靠性与选择结果的可信度。

2 理论方法

2.1 Shapley值

定义1：设集合N＝｛1，2，…，n｝包含有限个元素，∀S∈N都能与实值函数V（S）（V（Ø）＝0）建立一一对应关系，则（N，V）为n元因子对策，V为对策的特征函数，V（S）为对策的综合效度。

定义2：在n元因子对策下，因子i的权重计算公式为

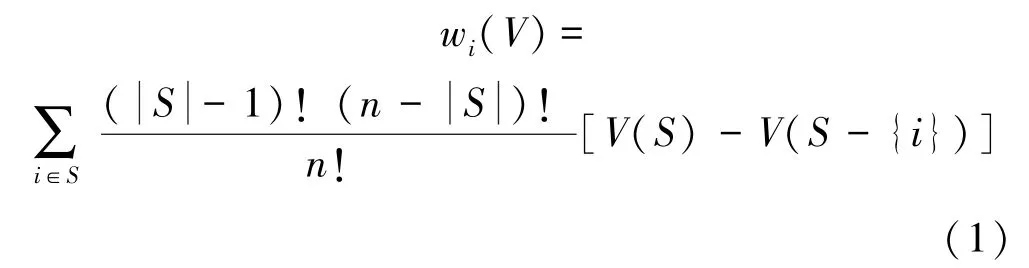
式中：S为集合N中所包含的i的子集；为子集S中包含的元素数量为子集S出现的概率。

2.2 概率犹豫模糊信息集成算子

2.2.1 概率犹豫模糊集

定义3：设X＝｛x1，x2，…，xm｝为非空集合，概率犹豫模糊集可定义为H＝｛［x，h（xi）］｜x∈X｝。其中：1，i＝1，2，…，m｝为概率犹豫模糊元（PHFE），γi为元素属于集合H的隶属度，pγi为相应的概率。

定义4：对任意PHFEh＝｛（γ（k），p（k））｜k＝1，2，…，l｝，其得分函数s（h）和偏差函数φ（h）可定义为s（h）、φ（h）∈［0，1］。

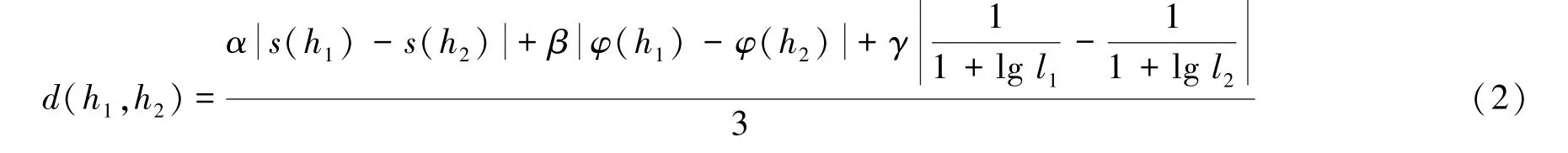
式中：α、β、γ∈［0，1］，设置α、β、γ的目的是防止“大数吃小数”现象，保证数据的精确性。

2.2.2 Archimedean范数

对已有研究分析可知［15］：严格的Archimedean－T范数可以用T（x，y）＝g－1［g（x）＋g（y）］表示，其中g为严格单调递减的加性算子：［0，1］→［0，＋∞］，g（0）＝1，g（1）＝0。根据对偶原则f（t）＝g（1－t），严格的Archimedean－S范数可以用S（x，y）＝f－1［f（x）＋f（y）］表示，其中f（t）单调递增，f（0）＝0，f（1）＝1。令为3个PHFE，定义Archimedean范数运算如下：h的补集hc＝λh＝｛f－1［λf（γ（k））］，p（k）｜k＝1，2，…，l｝（λ＞0），hλ＝｛g－1g（λγ（k）），p（k）｜k＝1，2，…，l｝（λ ＞0）。其中标准化概率

定义7：令hj（j＝1，2，…，n）为一列PHFE，w＝（w1，w2，…，wn）为权重向量，满足wj＞0且定义广义概率犹豫模糊有序加权几何算子（GPHFOWG）为

当g（t）＝－lnt时，GPHFOWG算 子 调 整 为PHFOWG算子：

2.2.3PHFMSM算子

定义8：设hi（i＝1，2，…，m）是一组PHFE，且r＝1，2，…，n。定义PHFMSM（r）算子为

其中（i1，i2，…，ir）包含组合（1，2，…，n）中所有的r元组，为二项式系数

用hi＝｛（γ（ijk），p（ijk））｜k＝1，2，…，l｝表示一列PHFE，且r＝1，2，…，n，w＝（w1，w2，…，wn）为对应的权重向量，满足wj＞0且，若则称PHFWMSM（r）算 子 为 概 率 犹 豫 模 糊 加 权Maclaurin对称平均算子。

2.3 决策模型

设决策方案集为T＝｛T1，T2，…，Tm｝，属性集为C＝｛C1，C2，…，Cn｝，属性权重向量w＝（wj｜j＝1，…，n）满足wj＞0且决策专家集，其权重向量η＝（ηt｜t＝1，2，…，e）满足ηt≥0且决策者根据属性集对决策方案进行综合评价，为了全面、准确表达决策者提供的决策信息，采用表示各属性指标Cj下方案Ai的评价信息，构建概率犹豫模糊决策矩阵H＝（hij）m×n。引入PHFWMSM（r）信息集成算子，结合MULTIMOORA方法，提出一种基于概率犹豫模糊MULTIMOORA的决策模型。

（1）权重计算。运用基于Shapley值改进AHP权重计算模型确定专家权重和指标权重。依据指标特性选取相关领域的专家e名，每名专家在了解其余e－1名专家在其各自领域的重要性的基础上，进行专家评估打分，依据专家打分，采用式（1）计算专家权重。采用1～9标度法建立对比判断矩阵，会出现指标权重区分度过大的现象，在指标较多的情况下，指标的相对重要程度不易清晰衡量，因而专家决策的不确定程度较高，因此提出改进的1～9标度法。在进行因素比较时，可以取1～9之间任意值，以避免因素之间难以比较的问题。Pt（t＝1，2，…，e）为e位专家依据改进的1～9标度法给出的比较矩阵，在通过一致性检验的前提下，各指标综合权重为

式中：Ptj（t＝1，2，…，e；j＝1，2，…，n）为根据第t位专家给出的比较矩阵Pt计算得出的第j个指标的权重。

（2）决策信息标准化。各决策方案在属性指标集下的综合属性信息采用PHFWMSM（r）信息集成算子得到。为标准化决策矩阵，其中，Cj为属性指标，hij为属性Cj下决策方案的评价信息，为hij的补集，D1为效益指标集，D2为成本指标集。

（3）计算方案的综合属性值。基于标准化决策矩阵，运用PHFWMSM（r）算子计算每个方案的综合属性值）。为了不失一般性，令r＝1，则：

当g（t）＝－lnt时，

（4）运用MULTIMOORA方法进行评价。基于比率法对决策方案Ti进行评价：ri1＝S（PHFWMSM（1）1）（i＝1，2，…，m），其中的得分函数，ri1越大方案越优。基于全乘模型对决策方案进行评价：ri2＝S（PHFWMSM（1）2）（i＝1，2，…，m），其中为PHFWMSM（1）2的得分函数，ri2越大方案越优。基于参考点法对决策方案进行评价：小方案越优。将基于MULTIMOORA法得到的评价值作为新的属性指标构造决策矩阵R，标准化处理后得到决策矩阵：

其中：

水环境治理PPP项目投资额大、范围广，通常涉及跨区域治理，内容种类复杂、治理周期长、持续时间长、运营维护要求高、资本回收慢等，具有科学严谨性、系统关联性、全局性、综合性、复杂性、跨区域性等特点。在考虑供应商可持续性和水环境治理PPP项目特点的基础上，从财务状况、技术实力、管理能力、信誉和技术解决方案5个方面建立水环境治理PPP项目可持续供应商选择评价指标体系，见表1。

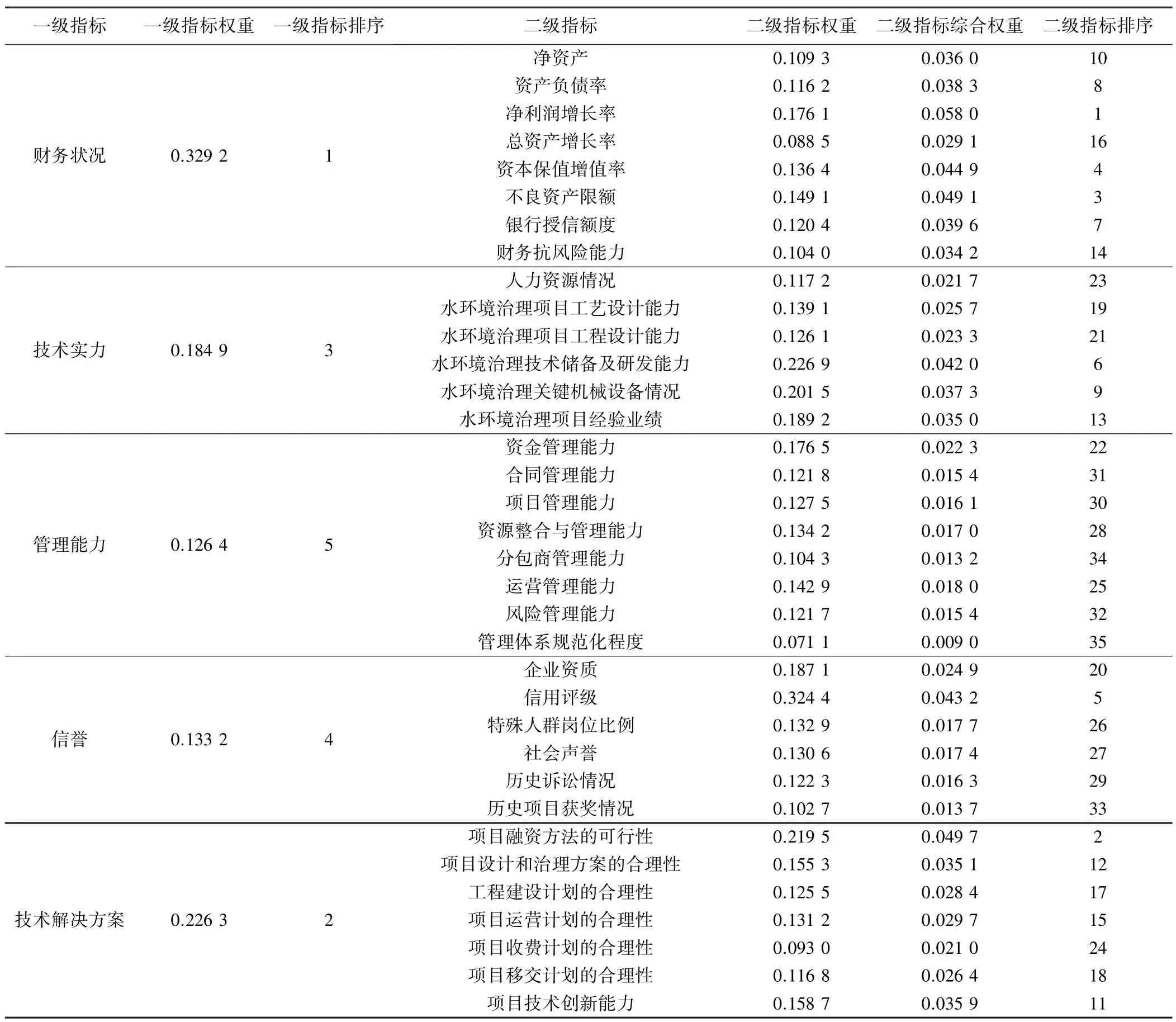
表1 可持续供应商选择评价指标体系及各指标权重

水环境治理PPP项目因具有综合性、技术性、跨区域性、系统性等而要求可持续供应商具备雄厚的技术实力、可持续管理能力、合理可行的技术解决方案等刚性条件。本文提出的水环境治理项目工艺设计能力、水环境治理项目工程设计能力、水环境治理技术储备及研发能力、资源整合与管理能力、项目设计和治理方案的合理性5个指标，既体现了水环境治理PPP项目的要求又能反映供应商的可持续性，附加净利润增长率、总资产增长率、资本保值增值率、不良资产限额、银行授信额度、资金管理能力、信用评级7个指标共12个指标用来弥补现有研究未考虑供应商自身可持续性的不足。

水环境治理项目工艺设计能力是指工艺人员编制工艺规程、设计工艺装备等的能力，其考察的是供应商在水环境治理工艺方案编制、工艺设计、人员配备等方面的能力。水环境治理项目工程设计，是在全面系统地分析水环境治理项目建设所需技术、资源等的基础上进行工程设计文件编制的活动，水环境治理项目工程设计能力是供应商工程设计资质、专业人员数量等因素的综合体现。供应商水环境治理技术储备及研发能力是评估供应商技术实力的重要指标，其能否满足水环境治理PPP项目设计、施工到后期的运营维护等技术性要求，是项目成功的关键因素之一。水环境治理PPP项目的跨区域性对供应商资源整合与管理能力的要求较高，资源整合与管理能力是指供应商合理分配资源、调度机械设备，统筹管理技术人员，组织协调参与各方有序进行项目建设，在环境资源受限的情况下按期或提前完成项目建设目标的能力。项目的设计和治理方案是整个PPP项目的灵魂，水环境治理PPP项目系统关联性、全局性对全流域规划设计方案以及每个独立水体的治理技术方案提出了较高要求，因此政府部门选择可持续供应商的过程中应该对其项目设计和治理方案的合理性进行重点考量。

净利润增长率是净利润的年变化率，反映企业的优良程度，净利润增长率越高，企业的发展越良好。总资产增长率反映企业资本积累和发展能力，是年末资产总额与年初资产总额之差同年初资产总额之比。资本保值增值率是指企业在经营活动中资本的实际增减变化，用来衡量企业资本的运营效益与安全性，该指标越大，表明企业的资本保全状况越好，企业实力越强。不良资产不能参与企业正常资金周转，如企业采购或生产的积压物资、潜亏挂账等。银行授信额度指商业银行批准的企业信贷业务存量管理指标，可以用来衡量供应商资金来源的稳定性、债务偿还能力等，反映供应商的资金筹措能力。良好的资金管理能力有利于水环境治理PPP项目目标的实现，可以从资金利用率、资金使用计划的合理性等方面对可持续供应商资金管理能力进行评价。信用评级是反映企业资信信息的重要指标。

4 实例分析

4.1 决策实例

平舆县水环境治理与生态修复项目拟采用BOT模式。项目采用公开招标方式选择服务供应商，4家供应商通过了资格审查，并按照招标要求提交了招标文件。依据所构建的评价指标，邀请水利专家P1、财务专家P2、环境专家P3和法律专家P4对通过资格审查的4家供应商Ti（i＝1、2、3、 4）进行评估决策。

（1）权重计算。4位专家相互评估、打分，得到专家综合得分，见表2。依据得分表，采用式（1）计算得到专家权重：w1＝0.254 9，w2＝0.255 5，w3＝0.265 3，w4＝0.224 3。

表2 专家综合得分

由4位专家对选取的评价指标进行比较，获得符合一致性要求的比较矩阵，基于专家权重，运用AHP方法计算得到各指标权重，结果见表1。

（2）决策矩阵标准化。将基于PHFWMSM（r）算子的MULTIMOORA决策模型运用于该案例，决策方案集为T＝｛T1，T2，T3，T4｝。由4位专家对4个供应商的可持续性在35个评价指标下进行评估，得到4个初始概率犹豫模糊决策矩阵，依据指标的性质（不良资产限额为成本指标，其他指标为效益指标），对初始概率犹豫模糊矩阵进行标准化，通过PHFWMSM（r）算子集成决策信息，得到综合概率犹豫模糊决策矩阵H~＝（）4×35，其中为

（3）计算综合属性值，结果见表3。运用MULTI⁃MOORA方法对供应商可持续性进行评价。基于比率法的4个供应商可持续性评价：r11＝0.125 4，r21＝0.103 7，r31＝0.111 8，r41＝0.104 2；基于全乘法的4个供应商可持续性评价：r12＝0.160 3，r22＝0.125 7，r32＝0.138 2，r42＝0.125 3；基于参照点法的4个供应商可持续性评价：r13＝0.011 8，r23＝0.014 3，r33＝0.012 9，r43＝0.014 6。

表3 各供应商综合属性值

构建决策矩阵R并标准化，得到标准化决策矩阵。

计算综合属性值：E1＝1，E2＝0.027 8，E3＝0.410 9，E4＝0.007 4。依据Ei值的大小对4个供应商进行排序，排序结果为T1＞T3＞T2＞T4，即T1为最优供应商，应选择其为该项目的中标人。

4.2 对比分析

不考虑供应商自身可持续性，即不考虑水环境治理项目工艺设计能力、水环境治理项目工程设计能力、净利润增长率、总资产增长率等12个指标，依据其他23个指标运用该模型为项目选择最佳供应商，运算过程与上述过程相似，不再赘述。计算得到综合属性值：依据值对4个供应商进行排序，排序结果为T3＞T1＞T4＞T2，即T3为最优供应商，应选择其为项目的中标人。

根据一级指标和二级指标排序可以看出，可持续供应商选择主要侧重于供应商的财务状况和技术解决方案，对其他方面也有关注。传统供应商选择主要侧重于管理能力和技术实力两方面，对其他方面关注较少，尤其是技术解决方案。从决策结果可以看出，两者最后选择的最优供应商不同，可持续供应商选择得到的决策结果与实际决策结果吻合，而传统供应商选择得到的决策结果与实际决策结果不一致，说明决策过程中考虑供应商自身可持续性具有合理性，可以提高决策结果的可靠性。

5 结 语

供应商的可持续性决定了水环境治理PPP项目的可持续性，因此在供应商选择中考虑供应商自身可持续性至关重要。基于供应商自身可持续性，从可持续公共采购角度，从财务状况、技术实力、管理能力、信誉和技术解决方案5个方面构建了水环境治理PPP项目可持续供应商选择评价指标体系，并提出了基于Shapley值改进的AHP指标权重计算模型和基于概率犹豫模糊和全乘比例多目标优化的MULTIMOORA方法的水环境治理PPP项目可持续供应商选择决策模型。最后以平舆县水环境治理PPP项目可持续供应商选择为例，对模型进行验证。案例分析中的计算结果与项目实际选择的供应商一致，表明本文建立的评价指标体系和决策方法合理，可为其他行业可持续供应商选择提供借鉴和参考。