基于VMD和IAO-SVM的电压暂降源识别方法
2023-02-21陈晓华王志平吴杰康陈盛语许海文孙中海杨国荣江剑民陈锦涛
陈晓华,王志平,吴杰康,陈盛语,许海文,孙中海,杨国荣,江剑民,陈锦涛
(1.东莞理工学院 电子工程与智能化学院,广东 东莞 523808;2.广东工业大学 自动化学院,广东 广州 510006)
随着电力电子设备和敏感负荷的不断增加,工业用户对电能质量提出了更高的要求。电压暂降是指电力系统中供电电压的均方根值突然降低到额定电压的90%~10%,持续0.5~30个周波之后又恢复到额定电压附近的电能质量问题[1-2]。电力系统中的电压暂降源有可能是单一的电压暂降源,也可能是复合的电压暂降源,它们都会给敏感设备带来严重的影响,因此,准确识别出电压暂降扰动源的类型有助于电压暂降的防范和治理。
现有的研究对于电压暂降源识别主要分为2个步骤:特征提取和分类方法的选择。对电压暂降源进行特征提取的方法主要有傅里叶变换[3]、小波变换[4]、S变换[5-6]、希尔伯特-黄变换[7]、经验模态分解[2,8]等。傅里叶变换会出现频谱泄露和栅栏效应;小波变换存在选取小波基函数困难并且分解层数不容易确定等问题;S变换存在时间窗固定且计算量大的问题;希尔伯特-黄变换会出现模态混叠现象;经验模态分解会出现虚假模态问题等。常见的分类方法有神经网络[9-11]、K-近邻图[12]、相似度匹配[13]、模糊综合评价[14]、支持向量机(support vector machine,SVM)[15]等,其中神经网络存在需要大量样本和训练时间比较长等问题,K-近邻图存在样本的近邻个数K难以确定等问题。对于小样本的识别,有学者利用SVM对电压暂降源进行分类,但不同的惩罚因子和核函数参数的取值会影响分类效果[15]。有些学者仅考虑单一的电压暂降源识别[14-22],然而实际的电力系统中可能存在复合的电压暂降源。文献[11]仅考虑复合的电压暂降源,对单相接地短路、感应电动机启动和变压器投切等大概率发生的单一电压暂降源并没有进行研究分析,方法缺少普遍适用性。有些研究没有考虑高斯白噪声对电压暂降源信号的影响[2-3,7,10-14,17-19,21-22],所提出的方法对信号含有不同高斯白噪声情况下的分类准确率有待研究。
针对以往研究方法存在的不足,本文考虑单一和复合的电压暂降源信号,利用变分模态分解(variational mode decomposition,VMD)方法分解电压暂降源信号的三相电压,分别得到6阶固有模态函数分量,然后分别计算6阶固有模态函数分量的奇异值熵和近似熵,将它们组合起来作为1组特征向量。针对SVM的惩罚因子、核函数参数选择困难和天鹰优化(aquila optimizer,AO)算法在寻优时容易陷入局部最优解的问题,利用改进的天鹰优化(improved aquila optimizer,IAO)算法对SVM的惩罚因子和核函数参数进行寻优,构建IAO-SVM分类器,再将提取到的特征向量进行归一化处理之后输入到构造好的IAO-SVM分类器中对样本进行训练与识别,并与K近邻(K-nearest neighbor,KNN)、极限学习机(extreme learning machine,ELM)、SVM和AO-SVM这4种分类器进行对比。仿真结果表明:对信号分别加入0 dB、10 dB、20 dB、30 dB、40 dB、50 dB和60 dB的高斯白噪声,IAO-SVM分类器的识别准确率在5种分类器中最高,有助于解决电压暂降源的分类问题。
1 特征提取
1.1 变分模态分解
VMD是由Dragomiretskiy等人在2014年提出的一种信号处理方法[23]。与经验模态分解相比,它在处理端点效应以及模态混叠问题方面更具优势,具体分解方法参考文献[23-24]。
1.2 奇异值熵
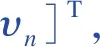
a)在奇异值的理论中,任何一个l×y阶的矩阵C可以分解为:
C=OVGT,
(1)

(2)
式中:O为l×l阶的正交矩阵;V为l×y阶的矩阵;G为y×y阶的正交矩阵;Λ=diag(δ1,δ2,…,δn)为对角矩阵,且n=min(l,y),对角元素δ1,δ2,…,δn均为矩阵C的奇异值,满足δ1≥δ2≥…≥δn≥0;令Q=OVGT,可以求得矩阵V,进而得到矩阵Q的奇异值δ1,δ2,…,δn。

(3)
(4)

c)根据信息熵的定义可得出奇异值熵
(5)
1.3 近似熵
通过VMD对电压暂降信号的一相电压进行分解得到n个IMF分量,假设每个IMF分量均为N维的时间序列{s(1),s(2),…,s(N)},每个IMF分量近似熵[26]的计算方法如下:
a)将时间序列{s(1),s(2),…,s(N)}按照序号次序组成N-m+1组m维向量,第e组m维向量
S(e)=[s(e)s(e+1) …s(e+m-1)].
(6)
式中:e=1,2,…,N-m+1;m为选定的模式维数。
b)定义S(e)和S(w)两者的距离ζ[S(e),S(w)]表示两者对应的元素中差值最大的一个,即有

(7)
式中:w=1,2,…,N-m+1,且e≠w。
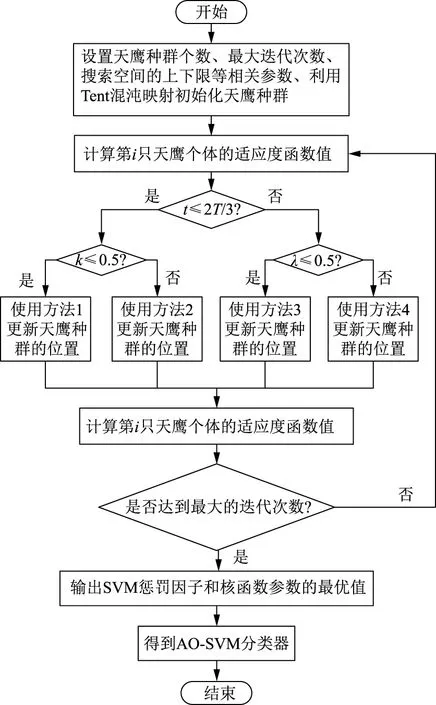
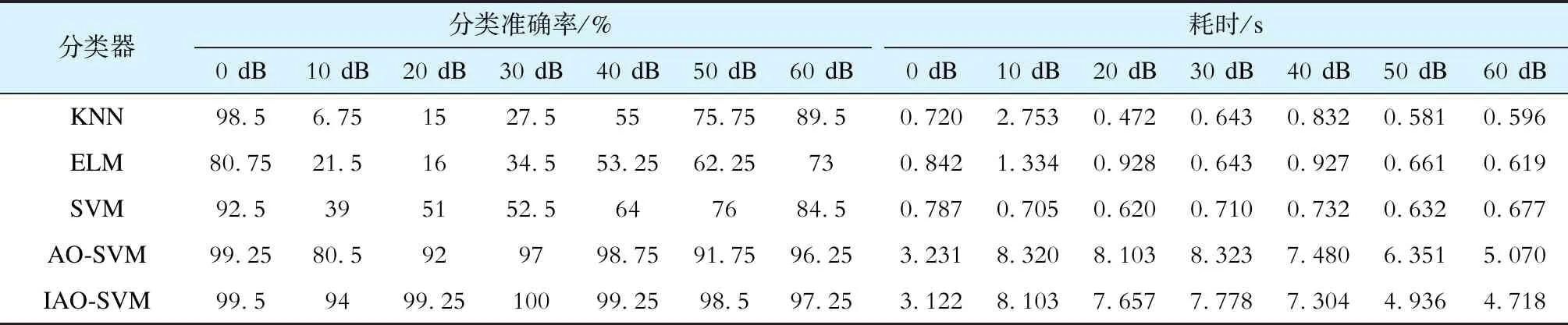
c)对于每一个e值,统计ζ[S(e),S(w)] (8) 式中r为选定的相似容限。 d)计算N-m+1个Ce,m(r)的对数平均值 (9) e)将m加1,重复步骤a)、b)、c)、d)计算Cm+1(r)的值。 f)第p个IMF分量近似熵 Ap=Cm(r)-Cm+1(r). (10) 式中:p=1,2,…,n。本文取m=2,r取原始时间序列标准差的0.2倍。将计算得到的n个IMF分量的近似熵A=[A1A2…An]作为特征向量。 对电压暂降扰动源信号的A相、B相和C相电压分别通过VMD获得6阶IMF分量,计算得到它们的奇异值熵HA、HB和HC,以及近似熵AA=[AA1AA2…AA6]、AB=[AB1AB2…AB6]和AC=[AC1AC2…AC6],将各相电压的奇异值熵和近似熵组合起来作为1组特征向量Θ=[HAAAHBABHCAC],在将特征向量Θ输入到构建好的分类器之前,先对所提取到的所有特征指标数据进行归一化处理,将其规整到[0,1]范围之内: (11) 式中:ρnorm为归一化后的数据;ρ为原始数据;ρmin为原始数据的最小值,ρmax为原始数据的最大值。 SVM[24]可以用来实现对小样本数据的模式识别,SVM的相关理论可参考文献[24]。 AO算法[27-28]是Abualigah等人在2021年提出的智能优化算法,其灵感来源于模拟自然界中天鹰捕捉猎物的行为,猎物的位置就是算法的最优解,通过仿生天鹰捕捉猎物来达到算法寻优的目的,该算法具有寻优能力强,收敛速度快等优点。AO算法的主要步骤如下。 a)按照式(12)初始化种群个体: (12) 对种群个体进行初始化之后可得天鹰种群的初始位置为: (13) b) 在AO算法优化的过程中,如果t≤2T/3(其中,t和T分别为算法当前迭代次数和最大迭代次数),那么执行探索步骤;否则,将执行开发步骤。AO算法的实现主要通过以下4个方法。 方法1,扩展探索。在方法1中,高空瀚翔的天鹰确定猎物所在的位置。该行为的计算表达式为: (Xmean(t)-Xbest(t)·η1), (14) (15) 方法2,缩小探索。在方法2中,当在高空瀚翔的天鹰发现猎物区域时,它会在目标猎物上方盘旋,准备着陆然后攻击猎物。该行为的计算表达式为: X2(t+1)=Xbest(t)·fLevy(d)+Xrand(t)+ (ϑ-χ)·η2. (16) (17) (18) ϑ=ϖ·cos(θ), (19) χ=ϖ·sin(θ), (20) (21) θ=-ω·γ1+Δ. (22) 式(19)—(22)中:ϖ1为每一个元素都在[1,20]范围的1行d列的矩阵,本文取d=2,ϖ1=[10 10];ψ和ω均为常数;本文取γ1=[1 2];Δ为1行d列的矩阵,本文取Δ=[1.5π 1.5π]。 方法3,扩大开发。在方法3中,天鹰锁定猎物的区域之后会试探猎物的反应。该行为的计算表达式为 X3(t+1)=(Xbest(t)-Xmean(t))·α- (23) 方法4,缩小开发。在方法4中,当天鹰接近猎物时,天鹰会根据猎物的移动攻击猎物。该行为的计算表达式为: (24) (25) G1=2·η4-1, (26) (27) 为了避免AO算法容易陷入局部最优的情况,本文对其进行改进,方法如下。 使用Tent混沌映射可以使得种群具有多样性和提高算法全局搜索能力,计算表达式为: (28) 式中η5为[0,1]范围内的随机数。 使用混沌映射产生的混沌数值替换随机参数可以使得算法在搜索空间中生成分布均匀和多样性的初始解[29],初始化种群个体的计算表达式可改写为 (29) 从图1可以看出,与随机序列相比较,利用Tent混沌序列生成的初始种群在搜索空间中分布更加均匀,使得算法易于跳出局部最优解,验证了利用式(29)初始化天鹰种群的合理性和优越性。 图1 不同方法初始化种群的分布图Fig.1 Initialized population distribution diagram of different methods 利用IAO算法对SVM的参数进行优化的步骤如下: a)设置天鹰种群U=30、最大迭代次数T=3、ψ=0.005 65、ω=0.005、α=0.1;ζ=0.1等参数,并利用式(28)、(29)初始化种群。 b)由于优化SVM的主要目的是获得最高的分类正确率,因此第i只天鹰的适应度函数值 φi=1-εa. (30) 式中εa为SVM的分类准确率。 以式(30)计算得到的分类误差率最小作为适应度函数,所以对于最小化问题,以适应度函数值较小的解作为当前最优解。更新ϑ、χ、G1、G2(t)、QF(t)等数值。 c)如果t≤2T/3,执行探索步骤;算法中生成一个随机数κ,如果κ≤0.5,则进行扩展探索,按照式(14)和式(15)更新当前解,并且计算适应度函数值,保留当前最优解;如果κ>0.5,则缩小探索,按照式(16)—(22)更新当前解,并且计算适应度函数值,保留当前最优解。 d)如果t>2T/3,执行开发步骤;算法中生成一个随机数λ,如果λ≤0.5,则进行扩大开发,按照式(23)更新当前解,并且计算适应度函数值,保留当前最优解;如果λ>0.5,则缩小开发,按照式(24)—(27)更新当前解,并且计算适应度函数值,保留当前最优解。 e)判断算法是否达到最大的迭代次数。如果已达到,那么输出惩罚因子和核函数参数的最优解;否则迭代次数加1,并跳至步骤b)继续寻优。 利用IAO算法优化SVM参数得到IAO-SVM分类器的流程如图2所示。 图2 获得IAO-SVM分类器的流程Fig.2 Flowchart of obtaining IAO-SVM classifier 本文研究的单一电压暂降源和复合电压暂降源参考文献[2]的方法,基于MATLAB/Simulink搭建如图3所示的改进IEEE 33节点配电网系统模型,研究单相接地短路(M1)、两相短路(M2)、三相短路(M3)、感应电动机的启动(M4)和变压器带负载的投入(M5)、感应电动机的启动和变压器带负载的投入同时发生(M6)、单相接地短路和变压器带负载的投入同时发生(M7)、单相接地短路和感应电动机启动同时发生(M8)这8种电压暂降扰动源。 图3 改进IEEE 33节点配电网系统仿真模型Fig.3 Simulation model of improved IEEE 33-buses distribution system 在仿真模型中,电源电压统一设置为10 kV,容量为30 MVA,频率为50 Hz,仿真时间步长设置为0.3 s。对于含单相接地短路的单一电压暂降源和复合电压暂降源,统一在图3中的A3侧测量电压值;变压器的投切在图3中的A1侧测量电压值;感应电动机的启动在图3中的A2侧测量电压值;对于同时发生感应电动机的启动和变压器的投入运行,在图3中的A2侧测量电压值。 不同的电压暂降源的样本数据可以由以下的方式获得: a)对于短路故障,改变发生短路故障的时间、发生短路故障节点的位置和线路负荷的大小; b)对于变压器带负载的投入运行,改变变压器一、二次侧绕组的联接方式,变压器的容量,变压器带负载投入的时间,发生变压器带负载投入的节点位置以及线路负荷的大小; c)对于感应电动机的启动,改变感应电动机的容量、电动机的类型、发生感应电动机启动节点的位置以及电动机启动的时间; d)对于同时发生感应电动机的启动和变压器带负载的投入运行,改变同时发生变压器带负载的投入和电动机启动的时间,改变发生的节点位置以及线路负荷的大小; e)对于含单相接地短路的复合电压暂降源,改变同时发生短路故障、变压器带负载的投入和电动机启动的时间,改变发生的节点位置以及线路负荷的大小。 通过以上不同的仿真方式获得M1—M8这8种电压暂降源类型各100组样本数据,每种电压暂降源类型的训练样本与测试样本的比例为1∶1。 在对信号分别加入0 dB、10 dB、20 dB、30 dB、40 dB、50 dB和60 dB的高斯白噪声情况下,分别对信号进行特征提取,将特征向量归一化处理之后输入到构建好的AO-SVM分类器和IAO-SVM分类器中进行分类识别,基于AO算法优化SVM的分类结果和基于IAO算法优化SVM的分类结果见表1,表1中0 dB—60 dB表示加入0~60 dB高斯白噪声的信号。 表1 AO-SVM分类器和IAO-SVM分类器的分类结果Tab.1 Classification results of AO-SVM classifier and IAO-SVM classifier 由表1可以看出,在对8种电压暂降源信号加入不同的高斯白噪声情况下,IAO-SVM分类器的总体分类效果都优于AO-SVM分类器。 为验证所提IAO-SVM分类器识别准确率的优越性,在保证每种类型电压暂降源的训练样本量均为50组和测试样本量均为50组的前提下,设置对照实验,将它与KNN、ELM、SVM和AO-SVM这4种分类器进行对比,通过仿真分析,可得这5种不同分类器的识别正确率的结果,见表2。 从表2中的数据对比可以看出,在对信号分别加入0 dB、10 dB、20 dB、30 dB、40 dB、50 dB和60 dB的高斯白噪声下,IAO-SVM分类器对8种电压暂降源的识别准确率都要比其他4种分类器高。 表2 5种不同分类器的识别正确率Tab.2 Recognition accuracy of five different classifiers 虽然KNN、ELM和SVM这3种分类器的耗时比AO-SVM分类器和IAO-SVM分类器都要少,但是在加入不同高斯白噪声的情况下,识别准确率均有较大幅度下降,并且均比IAO-SVM分类器低。 综上所述,在对信号分别加入0 dB、10 dB、20 dB、30 dB、40 dB、50 dB和60 dB的高斯白噪声下,IAO-SVM分类器的分类准确率和快速性都优于AO-SVM分类器,此外,IAO-SVM分类器的用时虽然比KNN、ELM和SVM分类器多,但在加入不同高斯白噪声的情况下,其分类精度比这3种分类器高得多,因此,IAO-SVM分类器对8种电压暂降源信号具有高效的识别能力和抗噪声能力。 本文提出一种基于VMD和IAO-SVM算法的电压暂降源辨识方法,为了更加科学和有效地提取电压暂降扰动源信号的特征,首先对电压暂降扰动源信号的A相、B相和C相电压分别通过VMD获得6阶IMF分量,计算它们的奇异值熵和近似熵,将它们组合起来作为1组特征向量;然后通过IAO算法对SVM的核函数和惩罚因子参数进行寻优得到IAO-SVM分类器;最后将特征向量输入到分类器中进行分类识别。为了验证所提方法的准确性和抗噪声能力,在对M1—M8这8种电压暂降源信号分别加入0 dB、10 dB、20 dB、30 dB、40 dB、50 dB和60 dB的高斯白噪声情况下,将IAO-SVM分类器与其他4种分类器进行对比分析,结果表明在兼顾识别准确率和抗噪声能力的情况下,IAO-SVM分类器是最优的选择。1.4 构建特征向量
2 IAO算法优化SVM参数的分类模型
2.1 SVM机的原理
2.2 AO算法

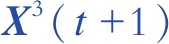
2.3 IAO算法

2.4 IAO算法优化SVM参数
3 仿真分析


4 结束语
