超高维缺失响应数据的特征筛选❋

邹丽英，刘 祎

(中国海洋大学数学科学学院，山东 青岛 266100)

随着科技水平的飞速发展和数据收集能力的大幅提升，超高维数据已经越来越频繁地出现在包括金融学、基因学、医学等各领域中。在高维数据中，为了选出对响应变量有重要影响的少数预测变量，许多惩罚方法被提出，例如LASSO[1]、SCAD[2]、自适应LASSO[3]和Dantzing[4]等。但在超高维数据中，即当变量个数相对于样本量呈指数增长时，这些方法面临着计算复杂性、统计准确性和算法稳定性的共同挑战[5]。为此许多学者提出超高维数据的特征筛选方法，用于解决面临的困难。Fan和Lv[6]基于线性模型提出了一种依赖于边际皮尔逊相关系数的确定独立筛选(Sure independent screening, SIS)，它可以将超高维数据降维至合适的大小，并且通过对相关系数绝对值大小进行排序，将对响应变量有重要影响的预测因子选中的概率趋于1。Zhu等[7]用一种针对一般多指标模型确定独立排序和筛选技术(Sure independent ranking and screening,SIRS)来排序重要变量。Li等[8]基于距离相关系数发展了SIS程序，但它对重尾数据不具有稳健性。Zhong等[9]在稳健距离相关的基础上提出了一种应用于单指标模型的特征筛选方法。然而上述特征筛选方法都是针对完全可观测数据的。

在实际案例中，例如成本效益分析、教育调查、全基因组关联研究以及基因表达研究等领域，由于部分受试者不愿意回答敏感问题，或者不可控因素导致的信息丢失，出现响应变量随机缺失(Missing at random，MAR)的情况是较为常见的。有关于缺失数据的统计分析，已有许多文献进行研究，例如：Wang和Rao[10]提出了处理缺失响应问题的经验似然方法。Qin、Shao和Zhang[11]将逆概率加权方法用于处理协变量相关的缺失响应数据。Hu、Follmann和Qin[12]研究了缺失数据平均响应的半参数降维估计。近年来，一系列研究开始集中于处理缺失响应变量的超高维数据，并提出高效、准确的特征筛选方法。Lai等[13]调整了Zhu等[7]的SIRS方法并结合逆概率加权技术，提出了一种无模型特征筛选方法。逆概率加权方法对缺失概率较敏感，因此非参数插补作为一种处理缺失数据的方法得到广泛应用。Fang[14]基于非参数插补技术提出了无模型的特征筛选方法，并说明其比逆概率加权方法具有更好的筛选效果。

本文提出了一种新的特征筛选程序(Imputed distance correlation，IDC)，构造插补响应变量与协变量分布函数之间的距离相关系数作为筛选指标进行特征筛选。所提方法不依赖于模型假设且对协变量异常值稳健，而且可以直接处理响应变量是多维的情形。通过数值模拟和微阵列弥漫性大B细胞淋巴瘤(Diffuse Large-B-Cell Lymphoma，DLBCL)数据分析，对方法的有限样本性质进行了验证。

1 方法

记Y为连续的响应变量，X=(X1,…,Xp)T为p×1维的连续预测变量。假设维数p相对于样本容量n呈指数增长，即log(p)=Ο(nα)，常数α>0。其中X是完全可观测的，而Y可能缺失。由于观测数据是不完全的，记(Xi,Yi,δi)为样本数据，i=1,…,n，其中δi为缺失响应的指示变量，即如果Yi缺失，则δi=0，如果Yi可观测，则δi=1。我们假设δ只依赖于X使得倾向得分函数有π(X)=P(δ=1|X)的形式。由Little和Rubin[15]可知，上述关于缺失机制的定义为随机缺失。Y是随机缺失的，简单来说，就是假设

P(δ=1|X,Y)=P(δ=1|X)。

基于稀疏假设，只有少数的预测变量与Y有关。我们定义活跃预测变量的索引集：

A={k:F(y|X)依赖于Xk,对某个y∈ψY,k=1,…,p}，

其中F(y|X)=P(Y≤y|X)为给定变量X条件下变量Y的条件分布函数，ψY为Y的支撑集，且|A|为集合A的势。在超高维数据分析中我们假设p≫n且p≫|A|。记Ac={1,2,…,p}A为非活跃预测变量的索引集，即Ac={k:F(y|X)不依赖于Xk,对∀y∈ψY,k=1,…,p}。令XA={Xk:k∈A}且XAc={Xk:k∈Ac}分别为预测变量的活跃集和非活跃集。

首先回顾一下距离相关系数[16]的定义。假设U和V为两个随机向量，维度分别为dU和dV。令φU(u)和φV(v)分别为U和V的特征函数，φU,V(u,v)为U和V的联合特征函数。距离协方差(Distance covaria-nce)定义为非负数dcov(U,V)，即

dcov2(U,V)=

U和V的距离相关系数(Distance correlation，DC)定义为

DC作为相关关系的一种度量，具有良好的特性，即dcorr(U,V)=0当且仅当U和V是相互独立的。这一性质使得距离相关尤其适用于超高维数据的变量筛选。并且对于超高维的完整数据集，Zhong等[9]在稳健距离相关的基础上提出了一种应用于单指标模型的特征筛选程序,这启发我们将稳健的距离相关应用于具有缺失响应的超高维数据中。

本文采用的稳健距离相关筛选指标是指

ωk=dcorr2(Fk(Xk),Y)=

处理缺失数据的插补方法是通过非参数回归得到的，设m(x)=E(Y|X=x)为给定X时Y的回归函数，则由核回归[17-18]可得到m(x)的估计为

根据插补后的数据集，我们得到筛选指标的估计为

2 数值模拟

在本节中我们将本文提出的插补距离相关方法(Imputed distance correlation，IDC)与其他处理超高维缺失响应方法作比较。对比方法有：Lai等[13]提出的基于逆概率加权的超高维特征筛选方法(Inverse probability weighted，IPW)，Fang[14]提出的基于插补技术的非参数特征筛选方法(Method of Imputation Technique，ITM)以及本文方法在完整数据下的情形(Distance correlation of full sample data，FDC)。在整个模拟研究中，我们将倾向得分函数P(δ=1|X)设置为逻辑回归模型，即P(δ=1|X)=exp(θX)/(1+exp(θX))，通过改变θ来改变缺失率(Missing rate，MR)，设置缺失率大约为0.2和0.4。对于每种情形，设置200次重复。

为了评估所提出方法的性能，我们采用Li等[8]的三个评估准则。第一个评估准则是包括所有活跃的预测变量的最小模型数，用S表示。我们给出了200次重复模拟中S的5%、25%、50%、75%和95%分位数。第二个评估准则是每个活跃预测变量的覆盖率，用Pi表示，我们给出了当给定模型大小为dn时200次重复模拟中Xi被选择的比例。第三个评估准则是所有活跃预测变量的覆盖率，用Pa表示。我们给出了在200次重复模拟中，对于给定模型大小dn，所有活跃预测变量均被选择的比例。我们选择dn为dn=[n/logn]，其中[x]表示x的整数部分。

实例1(线性模型)考虑线性模型如下：

Y=XTβ+ε。

表1 线性模型中单个活跃因子被选中的概率Ps及所有活跃因子被选中的概率Pa

从表1和2可以看出，在线性模型假设，以及协变量与响应变量都存在重尾数据下，本文提出的IDC方法相比于IPW和ITM两种方法而言，具有较为明显的优势。具体表现在活跃预测变量入选模型的比例更高，所需要的最小模型数更小。说明IDC方法可以将重要变量排在不重要变量的前面。完整数据下应用本文的FDC方法表现最好，因为其利用了样本的所有信息。

实例2(非线性模型1)考虑非线性模型如下：

其中β=(β1,β2,β3,0,…,0)T=(2,2.5,3,0,…,0)T∈Rp，即只有前三个变量是活跃的，X=(X1,…,Xp)T产生于均值为0，协方差矩阵为Σ的多元正态分布，ε服从N(0,1)。另外为进一步获得重尾预测变量，我们类似于Lai等[13]的设置，替换X1和X3为服从自由度为3的t分布产生的随机样本，替换X2为服从t(3)+1分布产生的随机样本，核函数与实例1相同。在此情形下，我们设置(θ1,θ2,θp)=(1,0.3,0.1)和(3,-0.5,2)得到约20%和40%的缺失率，选取(n,p)=(100,1 000)和(200,2 000)，模拟结果如表3和4所示。

从表3和4可以看出，IDC方法对非线性关系的检测能力要明显优于ITM和IPW方法。这是由于不同于ITM和IPW筛选指标的线性表达形式，IDC基于稳健距离相关指标，更适用于非线性模型的特征筛选。而且随着样本量的增大，方法的表现有明显改善。

表2 线性模型中最小模型数S的各分位数

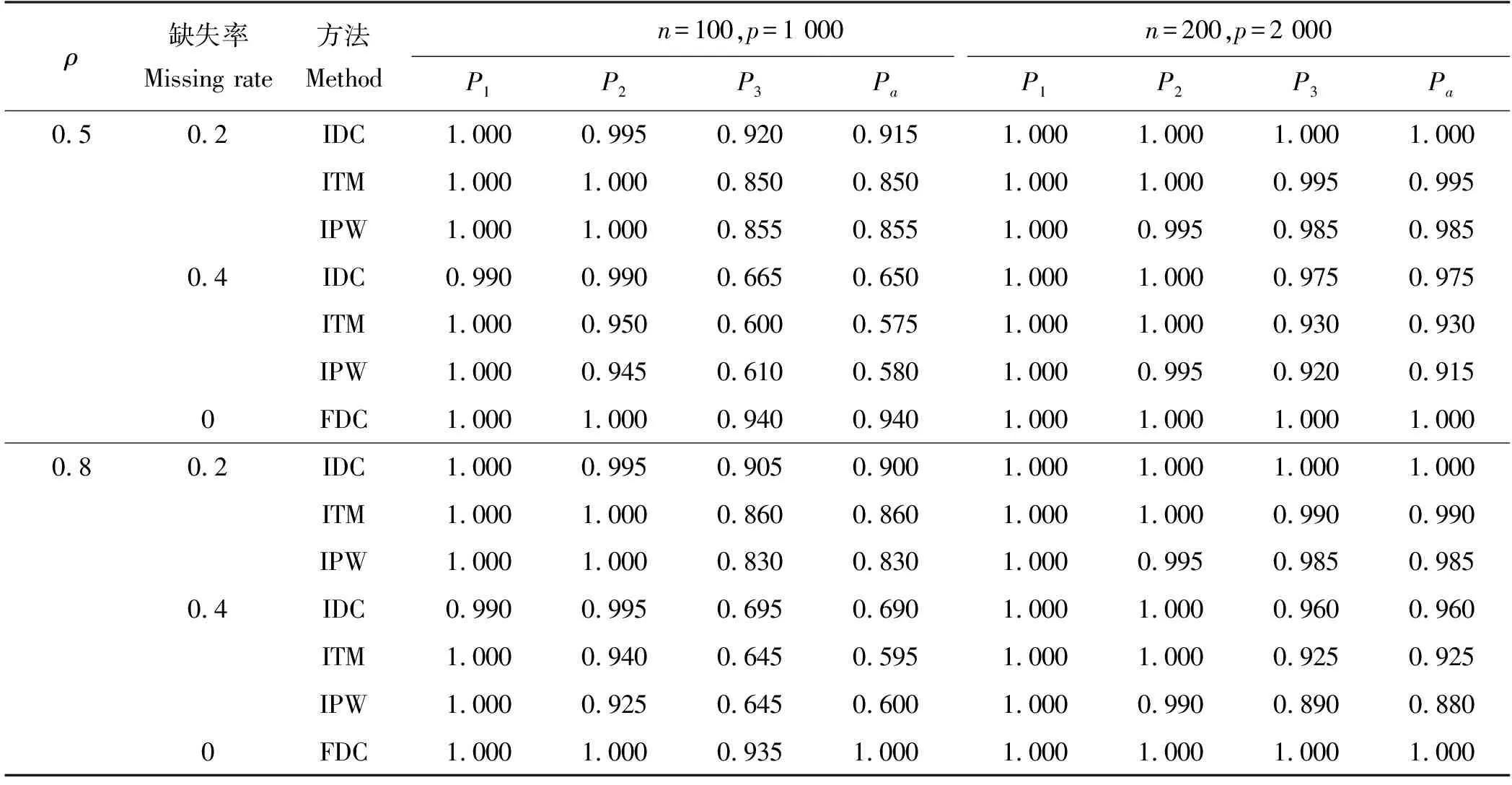
表3 非线性模型1中单个活跃因子被选中的概率Ps及所有活跃因子被选中的概率Pa

表4 非线性模型1中最小模型数S的各分位数

实例3(非线性模型2)为了进一步验证方法在非线性模型上的性能，考虑非线性模型如下：

cos(β21X1+β22X2+β23tanhX3)+ε，

其中(β11,β12,β13,β21,β22,β23)=(0.8,1,1.2,1.6,1.4,1.2)，即只有前三个变量是活跃的，其余设置与实例2中的设置相同。在此情形下，我们选取样本量n和协变量个数p为(n,p)=(100,1 000)和(200,1 000)，模拟结果见表5和6。

表5 非线性模型2中单个活跃因子被选中的概率Ps及所有活跃因子被选中的概率Pa

表6 非线性模型2中最小模型数S的各分位数

从表5和6可以看出，在更复杂的非线性模型中，IDC对比ITM和IPW两种方法的优势更为明显。ITM和IPW两种方法的接近于，即基本不可能选出所有的活跃预测变量，这可能是由于模型中存在示性函数及双曲函数，使得非线性关系复杂，变量筛选也变得更加困难。而且可以看到，随着样本量的增大，ITM和IPW两种方法并没有明显的改善。

实例4(双响应模型)考虑双响应变量模型如下：

其中β1=(β11,β12,β13,0,…,0)=(1,0.8,0.6,0,…,0)T∈Rp，β2=(β21,β22,β23,0,…,0)=(1,1.5,2,0,…,0)T∈Rp，即只有前三个变量是活跃的，其余设置与实例2中的设置相同。另外，我们对ITM方法中的筛选指标采取类似于文献[13]中公式(7)的二范数处理方式，使其适用于双响应模型的筛选指标计算。在此情形下，我们选取样本量n和协变量个数p为(n,p)=(100,1 000)和(200,1 000)，模拟结果见表7和8。

表7 双响应模型中单个活跃因子被选中的概率Ps及所有活跃因子被选中的概率Pa

表8 双响应模型中最小模型数S的各分位数

从表7和8可以看出，在多响应变量的非线性模型中，对比ITM和IPW两种方法，当缺失率提高时，插补技术较于逆概率加权方法表现较好，且在一定程度上也说明了IDC方法的指标对于复杂模型更具稳健性。

除了上述模拟，我们还验证了方法在小样本下的表现。在实例1的模型设置下，我们考虑了(n,p)=(50,500)和(n,p)=(50,1 000)两种情况，模拟结果见表9和10。从中可以看出各种变量筛选方法的表现趋势与大样本结果大致相同。

表9 在小样本的线性模型中单个活跃因子被选中的概率Ps及所有活跃因子被选中的概率Pa

另外，在实例1线性模型(n,p)=(100,1 000)的情况下，我们增加模拟了基于多重插补[19]的IDC方法,其中多重插补方法选取为10重插补(MI10-DC)，从结果可以看出，IDC和MI10-DC方法都优于IPW和ITM方法，这说明稳健距离相关的指标优势。但MI10-DC方法在Pa上表现劣于IDC方法，结合结果来看，可能是由于X3重尾分布对多重插补的抽样过程产生了影响。模拟结果见表11。

表10 在小样本的线性模型中最小模型数S的各分位数

表11 在线性模型中单个活跃因子被选中的概率Ps，所有活跃因子被选中的概率Pa及最小模型数S的各分位数

3 实际案例

我们应用提出的方法来分析微阵列弥漫性大B细胞淋巴瘤(DLBCL)数据，见Rosenwald等[17]及Zhu等[7]。为了对比，我们也采用IPW方法、ITM方法和FDC方法进行分析。DLBCL数据集共包含240例患者，其中随访期间死亡138例。因此，相应的响应变量由观察到的生存时间和删失指标组成，从每个患者的cDNA微阵列中获得的p=7 399个基因值是预测因子。另外，我们将数据划分为包含n1=160名患者的训练集和包含n2=80名患者的测试集。由于预测因子数量p远大于样本量n，为拟合原始模型，进行特征筛选是有必要的。

为进一步研究各种方法的表现，我们首先在训练集中分别利用IDC、ITM、IPW和FDC方法筛选基因并拟合Cox比例风险模型。然后，在测试集评估各种方法的预测表现，计算测试集的风险得分，将其分为低风险组和高风险组，其中，区分值是由训练集中估计得分的中值得到的。图1展示了四种方法下两个风险组病人的生存曲线的Kaplan-Meier估计[21]。

从图1我们可以看出，在MAR情况下，运用IDC方法的曲线分离得最好，且其对数秩检验产生的p值为0.001 2，而IPW方法和ITM方法对应的p值分别为0.037 9和0.261 2。在完整数据集的情况下，FDC方法的p值为0.039 8。

(虚线代表高风险组，实线代表低风险组。The dotted line is high-risk group, and the solid line is low-risk group.)

4 结语

本文提出了一种新的特征筛选程序(IDC)，首先通过插补技术，补全缺失响应变量值，再构造插补响应变量与协变量分布函数之间的距离相关系数，作为筛选指标。与传统的参数方法相比，所提出的非参数方法在稳健性、可扩展性和非线性重要变量检测能力方面具有一定的优势。本文提出的IDC方法基于插补技术创建了一个完整的数据集，便于使用标准的完整数据算法。相比于逆概率加权方法，由于一次插补只为每个具有缺失值的变量创建一个伪观察，因此其影响远小于基于缺失概率的逆概率加权方法的特征筛选程序，即我们的方法仅依赖于插补，减少了极端缺失概率的不利影响。通过数值模拟和实例可以看出，IDC方法较于对比方法在应用上具有一定的优势，但在确定筛选理论性质方面，基于稳健距离相关发展缺失响应变量的插补方法具有一定的难度，这也启发我们进一步改进筛选指标，优化处理缺失响应数据的超高维筛选方法。