基于RBF的隧洞岩体蠕变参数反演方法

2023-02-20李志刚王忠全张云山

水利科技与经济 2023年2期

李志刚，王忠全，张云山，徐洁，杨帆，黄铭

(1.中国水利水电第一工程局有限公司，长春 130033；2.合肥工业大学土木与水利工程学院，合肥 230009)

0 引言

近年来，为解决部分地区干旱缺水问题，水资源调配工程不断发展，隧洞穿越地层的地质条件也越发复杂，时常会遇到断裂、破碎、软岩等不良地质情况，对隧洞施工期和运行期安全造成威胁[1]。由于软岩的流变特性，在软岩地层开挖隧洞过程中，洞周围岩变形并不仅仅是瞬时完成的弹性变形，还有随着时间不断增长的蠕变变形，从而导致隧洞结构产生变形和破坏[2-3]。为了掌握隧洞开挖变形规律，准确预测洞周围岩蠕变变形，需要建立准确合理的数值模型。数值模型中，岩体的力学参数必不可少，而蠕变参数又是其重要组成部分[4]。

由于尺寸效应和工程因素的影响，通过现场或室内蠕变试验所获得的岩体力学参数往往不能反映现场大范围围岩的综合性质。因此，如何获取较为准确的蠕变参数成为制约岩体工程理论分析和数值计算的关键问题[5-6]。20世纪70年代以来，迅速发展的反演方法为解决这一问题提供了有效手段。近年来，国内外学者在参数反演方面进行了大量的研究工作[7-8]。Atsushi S等[9]采用能反映蠕变第三阶段的本构模型对隧道参数进行了研究，提供了隧道失稳对策；刘杰等[10]改进遗传算法，并应用于黏弹性本构模型上，利用普通遗传算法得到的优秀个体逐步优化搜索区间，提高运行效率。

虽然针对蠕变参数反演的研究成果较多，但对于实际工程来说，不同类型的围岩性质之间存在较大差异，蠕变参数与位移值之间关系复杂。RBF神经网络结构清晰，学习收敛速度快，且具有较好的全局逼近能力。因此，本文提出一种基于径向基函数(RBF)和FLAC3D仿真计算的隧洞岩体蠕变参数反演方法，并将该方法应用于滇中引水工程中。结合现场监测资料，采用与位移规律相符的本构模型，建立反映隧洞开挖支护工序以及长期蠕变过程的三维仿真计算模型。利用敏感性分析方法确定待反演参数。采用RBF神经网络联合仿真模型进行反演计算。研究成果为指导此类隧洞工程快速获取岩体蠕变参数，对隧洞开挖支护进行仿真计算，掌握隧洞开挖及长期洞周位移时空变化规律提供参考。

1 蠕变本构模型及参数反演方法

1.1 Burgers模型

岩体的蠕变过程十分复杂，构建合理有效的岩体蠕变本构模型，是开展参数反演并实现能够揭示合理变形规律的隧洞开挖数值仿真的前提。根据相关工程资料显示，本文分析的岩体埋深较大且地应力偏高，岩体流变效应明显，其岩体变形特征与伯格斯模型(Burgers)较为符合。

Burgers模型是一种四参数黏弹性模型，由Maxwell体和Kelvin体串联而成，能够反映岩体瞬时变形、衰减蠕变和等速蠕变阶段[11]。根据Burgers模型组成特点，基于连续介质理论可以求出模型的蠕变方程为：

(1)

式中：ε为应变；σ为应力，Pa；EM、ηM分别为Maxwell弹性模量、黏滞系数，EK、ηK分别为Kelvin黏弹性模量、黏滞系数，GPa、GPa·s。

本次数值仿真中，采用Burgers模型，该模型可以把复杂的蠕变过程直观地表达出来，能够反映洞周岩体的黏弹性蠕变特征。

1.2 RBF神经网络

软岩隧洞围岩力学参数复杂，为准确描述岩体变形与参数之间的非线性关系，采用具有超强非线性映射能力的神经网络。RBF神经网络即径向基函数(Radial Basic Function)神经网络，是一种前馈神经网络，因其结构清晰，学习收敛速度快，且能够逼近任意非线性函数而受到广泛应用[12]。因而，本文采用RBF神经网络对蠕变参数进行参数反演研究。

RBF神经网络由输入层、隐层、输出层3层结构组成。同层神经元之间没有联系，信号仅从上层神经元向下层传输，即输入层神经元只传递输入信号至隐层。

隐层神经元中的作用函数即基函数，对输入信号将在局部产生响应。最常用的基函数是高斯函数：

(2)

式中：X为n维输入向量；Ci为第i个基函数的中心(与X具有相同的维度)；σi为第i个变量，它决定该基函数围绕中心点的宽度；B为隐单元的数量；‖X-Ci‖为X与Ci之间的距离。

由式(2)可知，输入与中心的距离越远，节点的响应就越大。在RBF神经网络中，从输入层到隐层的变换是非线性的，隐层把输入向量从低维空间映射到高维空间，从而实现线性运算，网络输出为隐层神经元输出的线性加权和，即：

(3)

式中：ωij为隐层神经元与输出之间的连接权；M为输出维数。

1.3 基于RBF的蠕变参数反演流程

本文将建立基于RBF神经网络的岩体蠕变参数反演方法，该方法基本计算流程见图1。

图1 基于RBF神经网络的岩体蠕变参数反演计算流程

具体计算步骤如下：①根据工程现场监测资料和工程地质报告，并类比其他同类工程相关经验，综合分析选定合适的岩体蠕变本构模型。②采用敏感性分析方法，确定待反演岩体力学参数及其取值范围。③采用正交试验设计法，建立不同参数多水平的试验组合。④基于Flac3D建立的三维隧洞开挖蠕变数值计算模型，获取不同参数组合的围岩位移值并记录，构造RBF神经网络学习样本。⑤将样本代入RBF神经网络中进行训练，建立待反演参数与围岩位移之间的非线性映射关系。⑥将实测位移值输入到已经训练好的RBF神经网络中，反演得到相关蠕变参数取值。⑦将反演得到的蠕变参数代入数值计算模型中，得到不同测点的计算位移值，计算出测点实测值与计算值之间的误差，对反演结果进行检验和评价。

2 工程实例

滇中引水工程具有隧洞线路长、穿越地质条件复杂等特点。本文分析实例中的隧洞位于滇中引水工程楚雄段，隧洞全长4 755m，隧洞埋深一般在150～200m，最大埋深252m。隧洞穿越地层除隧洞进出口有第四系覆盖层之外，前段以滇中红层中的侏罗系、白垩系沉积岩地层为主，后段以昆阳群变质岩地层为主，且隧洞穿越软岩及较软岩的洞段占全长的48.7%。滇中红层软岩具有流变效应，对穿越滇中红层建筑物的长期稳定性具有较大影响。

2.1 数值计算模型

根据该隧洞工程地质情况和监测断面布置情况，选取隧洞前段建立三维数值计算模型。该洞段为IV类围岩，隧洞断面尺寸为9.86m×10.56m(宽×高)，断面形状为马蹄形，隧洞尺寸及监测点布置情况图2。

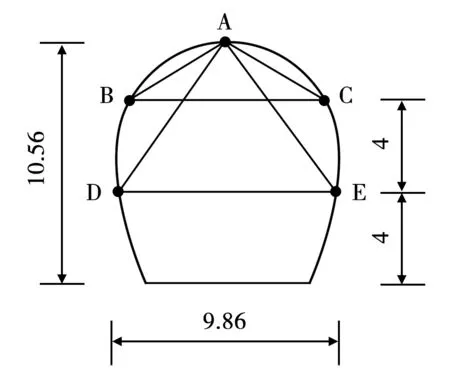
图2 隧洞断面监测点布置情况

根据圣维南原理，模型范围取5倍洞径，即左右及下部边界取距隧洞断面轴线50m，隧洞顶部取至地表面，洞长沿洞轴线方向取100m。由于隧洞穿越段风化层距隧洞较远，且该洞段岩性一致，故本文中采用同一岩层进行模拟。利用Ansys建立模型之后，导入Flac3D进行数值计算，模型见图3。围岩采用实体单元进行模拟，锚杆支护采用cable结构单元模拟，钢支撑采用beam结构单元模拟，钢拱架作用等效折算至混凝土喷层，喷层采用shell结构单元模拟。共划分单元80 445个。

图3 隧洞三维数值计算模型

模型四周和底部边界均采用法向约束，顶面为自由边界。隧洞开挖采用上下台阶法，循环进尺2m，上下台阶共计100个开挖步，每次开挖后进行锚固支护，支护落后于掌子面0.5m，开挖完成后，再进行共计150天的蠕变计算。

2.2 蠕变参数反演

2.2.1 敏感性分析

在进行围岩蠕变参数反演计算时，首先要确定待反演参数。由于围岩力学参数数量较多，为了提高参数反演结果的质量及精度，更准确揭示洞周围岩变形规律，可根据“敏感性原则”，选取对围岩长期变形影响较大的参数作为待反演参数。

本文主要对围岩基本力学参数进行敏感性分析，以隧洞拱顶以及左右拱肩沉降位移值作为参数敏感性大小的判别依据，利用极差法进行分析。首先采用正交试验设计法对弹性模量、泊松比、黏聚力、内摩擦角建立L9(33)正交表，利用2.1一节所建立的数值模型计算得到各测点位移值。在此基础上，采用极差法进行分析并得到结果，以拱顶为例，各参数对拱顶沉降值的影响见图4。

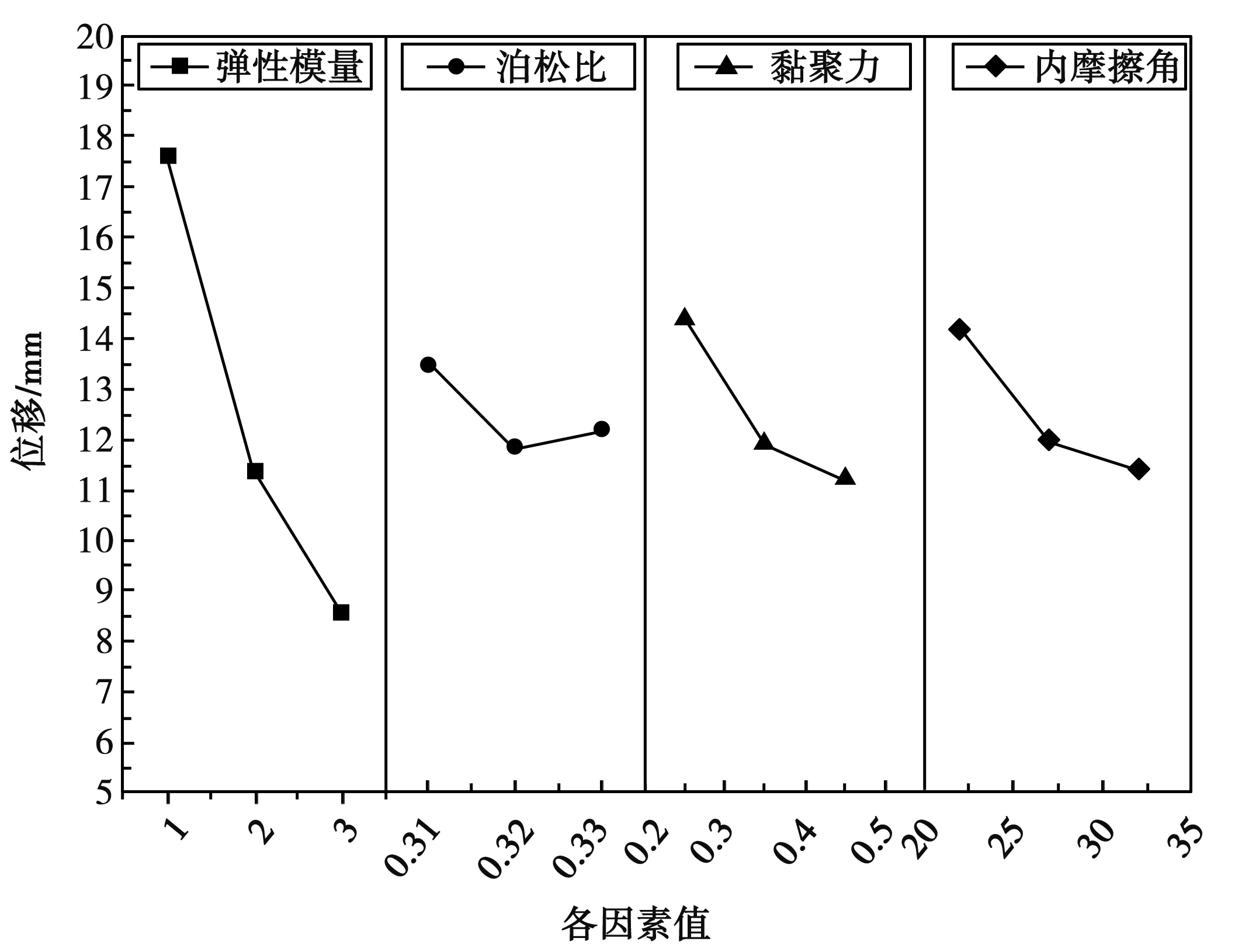
图4 各参数对拱顶沉降值的影响图

由图4可知，对围岩变形影响最大的是弹性模量E，黏聚力和内摩擦角次之，最弱的是泊松比。当保持弹性模量E不变，黏聚力从0.25MPa增大至0.45MPa时，拱顶沉降值变幅为0.4mm；内摩擦角从22°增大至32°时，拱顶沉降值变幅为0.3mm，与弹性模量对变形的影响相比可以忽略。所以，本文选取弹性模量E作为待反演参数。

由于本文研究的红层软岩在隧洞开挖时的变形具有明显的蠕变特征，Burgers模型的4个参数分别控制弹性变形和黏滞流动变形，其值均对位移有较大影响。为了更准确描述隧洞长期蠕变变形规律，Burgers模型的4个蠕变参数均作为待反演参数。

2.2.2 构造训练样本

根据敏感性分析结果，结合工程地勘资料，并类比滇中同类工程，综合分析确定待反演参数取值范围，见表1。