Charge self-trapping in two strand biomolecules:Adiabatic polaron approach
2023-02-20ChevizovichZdravkoviChizhovandIvi
D Chevizovich, S Zdravkovi´c, A V Chizhov, and Z Ivi´c,4,5
1University of Belgrade,Vinˇca Institute of Nuclear Sciences,P.O.Box 522,Belgrade 11001,Serbia
2Joint Institute for Nuclear Research,Laboratory for Radiation Biology,Dubna 141980,Russia
3Dubna State University,Dubna 141980,Russia
4Department of Physics,University of Crete,P.O.Box 2208,Heraklion 71003,Greece
5National University of Science and Technology MISiS,Leninsky prosp. 4,Moscow 119049,Russia
Keywords: charge self-trapping,adiabatic polaron,soliton,two-stranded biomolecules
1. Introduction
Stable charge transfer through biomolecules over large distances(which can be comparable to the length of the macromolecular chain itself) has attracted a great deal of attention from researchers in various fields of natural sciences for a long time. This process is important for many biological phenomena,such as photochemical reactions,photosynthesis,and metabolism of living cells.[1–8]In the DNA case, charge migration is directly related to damage of DNA and error replication,as well as to sensing of DNA damages by living cells and process of their repairing.[9,10]As we know,DNA damage can reduce fidelity in replication of the DNA molecule and consequently, it can be the source of genomic mutations.[11,12]All we have mentioned is a strong motivation for research in this field of biophysical science.Another impetus for studies of the charge migration in biomolecules is the possibility of their applications in nanotechnology and molecular electronics.[13]It seems that biomolecules(including DNA)can provide further miniaturization of microelectronic devices. Although numerous studies of the charge properties and the transport through biomolecules have been carried out so far,we still do not understand this phenomenon at a satisfactory level.[14–26]
From the viewpoint of quantum mechanics,migration of a charged particle through biomolecules takes place via electron transitions among the states that are close to the chemical potential of the system. In the case of DNA, such states are composed of theπandπ*bonds (i.e., the pzorbitals of the carbon–carbon double bonds in the nucleotide bases). The overlapping of these bonds allows the charge to migrate from one base to the neighboring one, which results in the charge migration along the macromolecule.[27]
The degree of overlap of intermolecular bonds among the neighboring structure elements can be significantly influenced by their dynamics,which is induced by the thermal influence of the biomolecule environment. In addition,the dynamics of the structural elements of a regular (crystal, molecular crystal,etc.) structure may cause another interesting phenomenon:the polaron effect. Due to the charge–phonon interaction,the charge can be self-trapped and the polaron effect appears.What kind of polaron can be formed depends on the properties of the structure as a whole.[28–30]It is generally accepted that due to the electron self-trapping in biomolecules,the adiabatic polaron appears.[31–38]Such quasiparticles can propagate over large distances in soliton form with minimal energy loss and without pulse distortion. Although there are some doubts about the possibility of soliton formation in polypeptide molecular chains,[39]such models continue to be the theoretical basis for studying these phenomena in biomolecular structures. In addition, some experimental results related to biomolecules appear to support a soliton picture of longdistance charge migration.[19,40]This is the reason why the soliton models in the problem of long-distance charge migration deserve special attention.
We have emphasized the importance of two physical parameters, which significantly affect the properties of charge carriers in biomolecules, as well as the possible formation of solitons: the overlap of the molecular orbitals (MOs) and the strength of the charge–phonon interaction. To construct a satisfactory theoretical model for describing the properties of charge carriers in biomolecules,several important facts related to these parameters should be kept in mind. Let us start with the strength of the charge–phonon interaction. Unfortunately,the mechanism of charge–phonon interaction in biomolecules is still poorly known. A brief but concise description of this problem in the case of DNA can be found in Ref. [10]. We will mention here only that there are no strong arguments that would definitely determine the strength of this interaction. Depending on the considered investigations its value explores the whole regime from the weak to the strong coupling limits.[10,41]In addition,the strength of charge–phonon interaction can be masked by some other effects, for example, by the effects appearing due to the inherent DNA disorder. In complex biomolecules consisting of two or more molecular chains,MO overlap is possible between adjacent structure elements located on the same molecular chain,but also between neighboring structure elements located on different molecular chains.The MO overlap magnitudes usually are calculated using numerical models,which are often based on some adopted assumptions. Therefore, the literature values may differ significantly,depending on the source referenced.
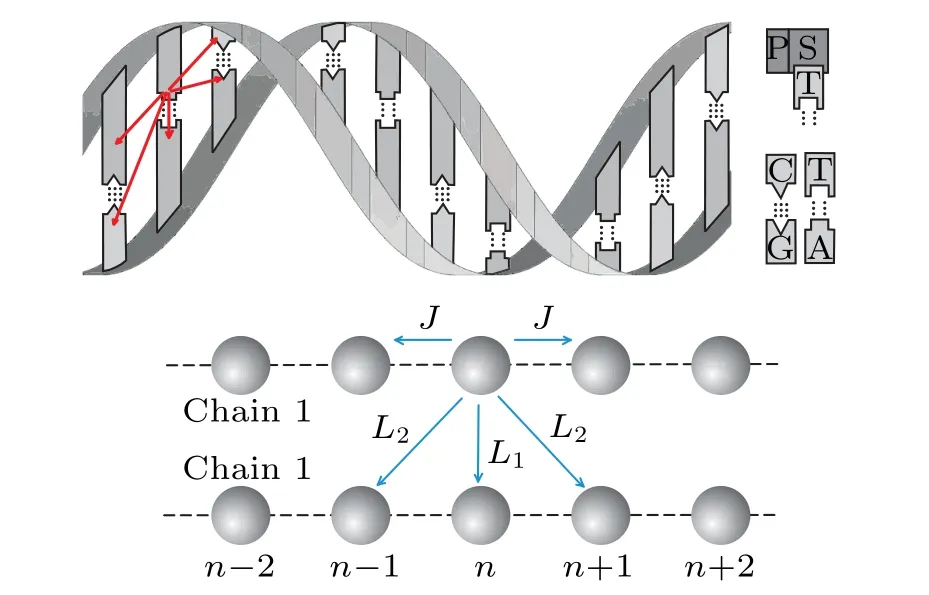
Fig.1. Upper: schematic structure of the double helix DNA macromolecule. The AT(CG)are pairs of nucleobases placed on the opposite strands, connected by the hydrogen bonds. The backbone of the DNA strand consists of alternating phosphate and sugar groups. Lower: simplified structure of two-strand DNA–like macromolecule. Nucleotide bases(together with a corresponding phosphate-sugar molecular group)are presented by spheres,regularly distributed along the strands.
To clarify which values of overlap of MOs for biomolecules consisting of two macromolecular chains correspond to soliton states, we consider the single excess charge injected into a two-strand macromolecular structure in the framework of the adiabatic polaron(soliton)theory. Here,we suppose that soliton appears due to the charge–phonon interaction. We assume that the structure is homogeneous(all structure elements from which the system is built are identical). It is taken into account that the overlap of the MOs can occur between the two adjacent structure elements(nucleotides)belonging to the same strand,as well as between those belonging to different strands,as is schematically presented in Fig.1.We consider the influence of such an MO overlap on the energetic stability of eventually formed soliton states,as well as on their inertial properties and soliton velocity.
2. The model
To set up the theoretical framework of our investigation,we consider an extra charge(excitation in general)in a structure consisting of the two coupled identical macromolecular chains, each composed ofN ≫1 identical structural elements (molecular groups). The physics of charge migration in such structures is usually described in the framework of the common tight-binding model, modified to take into account the overlaps of MOs between neighboring structure elements. Besides particle subsystem,our theoretical model includes phonon subsystem and the charge–phonon coupling:
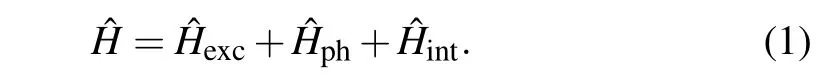
The overlap of electronicπ-orbitals among the neighboring nucleotide groups lead to delocalization of the charged particle from a particular structure element and its migration to neighboring ones. Such delocalization can take place along the same strand(intra-strand migration),or between two structure elements belonging to different strands (inter-strand migration). Excitation Hamiltonian describing the extra charge can be expressed as
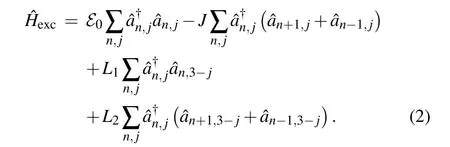
Herenlabels the lattice sites along the strands (it takes the values from-N/2 toN/2)and the indexjenumerates a particular strand (j=1,2). Consequently, the position of each structure element in the system is determined by two “coordinates”(n,j). Operators()correspond to the charge creation(annihilation)on the position(n,j). Theℰ0is the energy of charge excitation on the corresponding(n,j)molecule andJis intra-strand transfer integral(TI)(resonant energy of the charge transfer between the neighboring structure elements belonging to the same strand, which is determined by the MO overlap of two neighboring molecules placed on the same strand). Finally,L1andL2are inter-strand TIs of the charge transfer between the neighboring structure elements belonging to different strands(see schematic picture on Fig.1).L1is the transversal inter-strand TI, determined by the MO overlap of two nearest neighboring molecules((n,j)↔(n,3-j))and theL2is the diagonal inter-strand TI,determined by the MO overlap of two first neighboring molecules((n,j)↔(n±1,3-j)).In the case of Peierls dielectrics,it is commonly adopted thatL1<0, but in some substances, this parameter may be of the opposite sign or it may alternate along a strand! Here, we adopt thatL1(L2) can be either positive or negative, and has an identical value in the whole structure. Since the distance between structure elements located at(n,j)and(n±1,3-j)is larger than the distance between structure elements (n,j)and(n,3-j),it is reasonable to assume that|L2|≤|L1|. Although it is usually considered to be|L1,2|≪|J|,in our analysis we allow that|L1,2|can be taken from the whole interval(0,|J|).[10,48]
In the case of the phonon subsystem, we have assumed that the mechanical oscillations of both strands are mutually independent. This can be justified by the fact that the interaction energies of adjacent two structure elements from different molecular strands are significantly less than the interaction energies of two adjacent structure elements belonging to the same strand. The Hamiltonian describing the phonon subsystem is


In addition,we suppose that the injected charge interacts with acoustic phonon modes only. Such an interaction is determined through the charge–phonon coupling parameterFq. In the case of the interaction with acoustic phonon modes,it has the formFq=2iχsin(qR0), whereR0is the distance between two adjacent structure elements of the same strand,ωq=ω0sin(qR0/2) is phonon frequency, andω0=2. The parameterχis the strength of charge–phonon interaction,κis the stiffness of the chain,andMis the mass of the molecular group at the chain siten. Finally,we adopt linear dispersion law for phonons:ωq=c|q|,wherec=ω0R0/2 is the speed of sound.
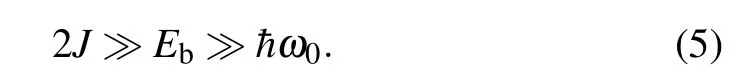
To discuss the properties of the extra charge in the double–chain molecular structure, we suppose that it forms soliton-like large polaron excitation. According to the general theory of the polarons,its nature depends on the values of the basic energy parameters of the system: intra-strand TI(J),so-called polaron binding energyEb=∑q=and characteristic phonon energy¯hω0.[2,30]In the case of the large polarons we have Here, the adiabatic condition (2J ≫¯hω0) provides that the fluctuations of exciton and macromolecular subsystems are uncorrelated.[30]As a consequence, the mean values of the products of the exciton and phonon operators may be factorized, and theoretical treatment can be carried out within the semi-classical approximation.[30,36,42,43]Physically, this means that the deformation of the lattice formed due to the interaction of exciton with the phonon subsystem is slow compared to the exciton subsystem and it can not follow the particle motion (lattice deformation forms a “frozen” structure).Strong coupling conditionEb≫¯hω0provides that the potential well that appears due to the lattice distortion is deep enough to prevent the destruction of the formed polaron state(it provides the polaron stability). On the other hand, this coupling should be weak enough and the polaron can span a large number of lattice sites. Consequently, continuum approximation is applicable. Such a condition is satisfied in the case when 2J ≫Eb.[30,36,44]In those cases,the variational approaches (like Pekar’s variational ansatz) are promised tools for the investigation of such systems.[36,42,43,45,46]
As it was mentioned, the serious problem for biomolecules is the fact that the values of their basic energy parameters are generally poorly known. Let us, therefore,start with those for which there is consensus about their values. Typical values of the phonon energy in biomolecules range from a few tens of meV (α-helix macromolecules),up to 120 meV in polyacene molecule, and 200 meV in the double–strand polyacene. Here,we adopt that the phonon energy of the DNA is about 7 meV.[47]This value corresponds to the phonon frequencyω0=1013s-1.
The values of the transfer integrals usually are estimated fromab initiocalculations. There are quite different literature data of these parameters,depending on the model for their calculations. For conjugated polymers, a typical value of TI is about 2.5 eV,while for alpha-helix this parameter is estimated to be an order of a few eV. In the case of DNA, estimated values of the intra-strand and inter-strand TIs range from a few tens of meV[48]to several hundreds of meV,[20,49–53]depending on the applied model. For our purposes, in the case of intra-strand TI, we will refer to the valueJ= 0.3 eV(0.48·10-19J) which corresponds to the upper estimation of this parameter in DNA.The values of the inter-strand TIs will be varied,from small values(compared withJ),up to the values of the order ofJ.
An additional serious problem is the poor knowledge of the strength of the electron–phonon interaction: depending on the literature data, the estimations of this parameter range from those corresponding to a weak electron–phonon interaction, up to those indicating a strong interaction of the charge with mechanical oscillations of the structure.[40]Here,we use the valuesχ=0.6 eV/A (χ ≈0.96×10-9J/m)[47]andM=5.1×10-25kg,[33]which leads to the estimation ofEb≈0.46 eV.
According to the adopting data, it seems that the criteria Eq. (5) is (less or more) satisfied for many biomolecules,including DNA. To study the dynamics of our system,we use a time–dependent extension of Pekar’s variational ansatz,[36,42,43,45,46]that allows the simple factorization charge and phonon variables:

The functionsψn,j(t) andβq,j(t) are treated as dynamical variables. From the condition of the minimum of the functionalℋ=〈ψ| ˆH|ψ〉, we find the equations of the motion for the amplitudesψn,j(t) andβq,j(t): ih¯=and ih¯=.[2]Here,the functionalℋis

Consequently, for the charge amplitudes we have the set of equations:
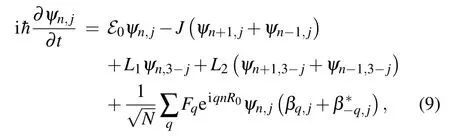
while for phonon amplitudes we have

Now, we pass to the continuum limit (ψn,j(t)→ψj(x,t),nR0→x, ∑n →). The set of Eq. (9) attains the form of two coupled partial differential equations:


while for the phonon amplitudes we have
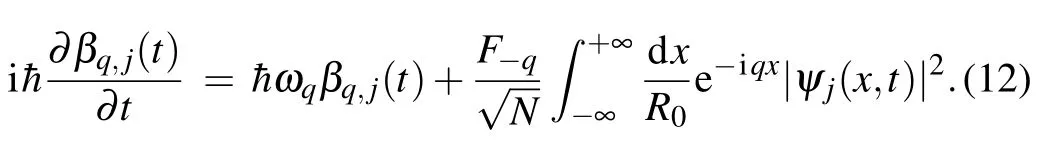
In the obtained system of Eqs.(11)and(12)we have coupled charge and phonon amplitudes. In the following, we eliminated the phonon variables from Eq. (11). Since we investigate the charge propagation in the form of a stable “wave pulse” (soliton-like form), we assume that charge probability density depends on time and space coordinate through the coordinateξ=x-vt:|ψj(x,t)|2=|ψj(ξ)|2, wherevis soliton velocity. In that case, Eq. (12) becomes an ordinary differential equation of the first order, and it can be easily integrated. The general solution of this equation has the formβq,j(t)=e-iωq·t+(t). Here, the first term is the homogeneous solution that corresponds to the incoherent part of lattice displacement coming from free lattice modes,and it can be disregarded in adiabatic treatment.[36]Because we search for a stable stationary polaron solution,the main contribution to polaron formation comes from the particular solution (i.e.,from the second term). The particular solution to Eq.(12)is

After the substitution of(t) into Eq. (11), we find the system of the two coupled nonlinear Schr¨odinger equations(NSE)for polaron amplitudesψ1(x,t)andψ2(x,t):

whereG=is the nonlinearity parameter andu=v/cis soliton velocity,normalized on the speed of sound. Physically irrelevant term (ℰ0-2J)ψj(x,t) is absorbed by the transformationψj(x,t)→ψj(x,t).
3. Finding for soliton solutions
Systems of equations similar to Eq. (13) have appeared and have been studied in various problems,especially in nonlinear optics and biophysics.[36,54–60]The explicit solutions of this system have not been fully examined until now, but its properties may be examined by different approximate approaches. In that sense,the average profile approximation can be very useful[36,57–59]because it allows analytic calculations whose accuracy has been demonstrated by comparison with the numerical analysis. The main idea of such an approach is the assumption that the solutions of the coupled system of NSE are not substantially different from those of the uncoupled ones. As a consequence, we will search the stationary solutions of Eqs.(13)in the form

HereAjare real amplitudes of the soliton propagating along thej-th molecular chain,kandΩare wave vector and the frequency of the soliton carrier wave. The real functionφ(x-vt)is the envelope of the charged particle wave function we will look for in the form of a wave pulse.Consequently,initial conditions for envelope function in “moving” coordinate frame(defined by the coordinateξ)are
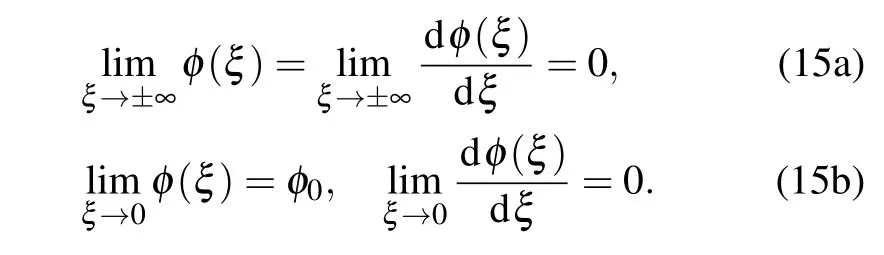
As DNA-like macromolecules consist of two identical molecular strands, we assume that the soliton wave has an identical form on both strands. This means that the envelope functionφ(ξ)does not depend on the molecular strand along which the soliton is extended. Normalization condition for charge function in continuum approximation becomes
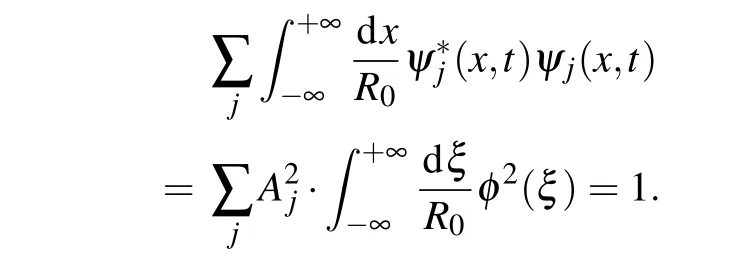
If we additionally require that the envelope of the charge wave function be normalized,the normalization condition becomes
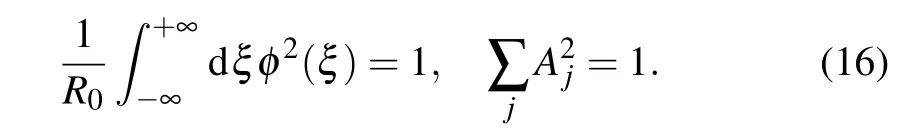
Thus, Eqs. (13)–(16) represent the mathematical framework of our study. In what follows, we will analyze these equations and find under what conditions soliton solutions can occur. We find non-trivial solutions to Eq. (13) by substituting Eq.(14)in Eq.(13)and then we separate the real and the imaginary parts of the obtained equation. From the imaginary part we obtain the set of algebraic equations for amplitudesA1andA2:

which has a non-trivial solution when the determinant of the system is equal to 0. Under this condition, we find that the wave vector of the carrier wave is


this equation has the pulse-like soliton solution
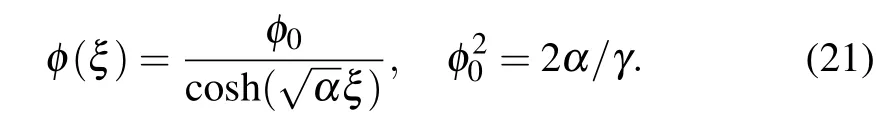
Hereφ0is the soliton amplitude, determined by the ratio of theαandγ. The parameterαdefines the width of the soliton pulse. Characteristic soliton parameters for the hybrid soliton solution can be expressed by the basic energy parameters of the system in the form
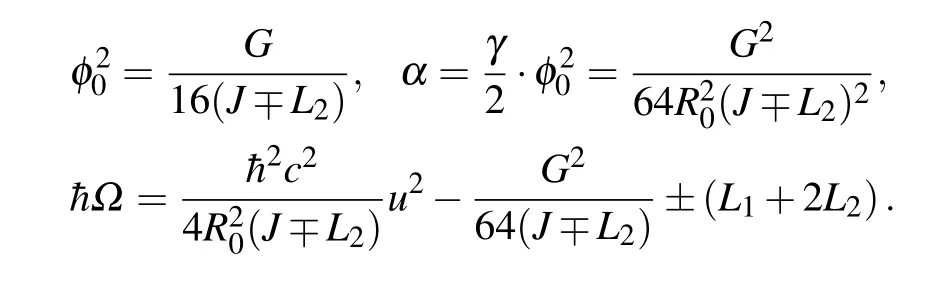
It is interesting to note that,φ0, andα(which is connected with the pulse width) are not affected by the transfer integralL1,but in addition to the dependence onJ,these soliton parameters depend onL2. This result indicates a possible large impact of the MO diagonal overlapL2,especially if it is comparable to the intra-chain overlapJ.
As it is mentioned above, the system parameter space in the framework of the adopted model is determined by the set of parameters (¯hω0,Eb,J,L1,L2). In the theory of the exciton self-trapping in 1D and quasi 1D crystal structures, it is very comfortable to describe the system in terms of the socalled adiabatic parameterB=2J/¯hω0,and the coupling constantS=Eb/¯hω0.[30,33,36,39]The first parameter determines the character of the lattice deformation engaged in the polaron formation (whenB ≫1, the adiabatic limit is reached). The interrelation of these two parameters determines the polaron spatial size and the degree of quasi-particle dressing: in the strong coupling limitS/B ≫1 we have adiabatic small polaron,while in weak adiabatic limitS/B ≪1 we have adiabatic large polaron(soliton).
The parametersSandBare quite sufficient to describe self-trapping states in pure 1D structures. However, to treat structures that have a larger number of dimensions (or the structures that are composed of several 1D strands that interact with each other),it is necessary to introduce additional parameters which will take into account additional interactions among the strands. For our purpose,we define two additional parametersp1=L1/Jandp2=L2/J. Further, we describe the state of the extra charged particle in a double-chain structure by the set of parameters (S,B,p1,p2). In addition, the soliton velocity should be added to the parameters that determine the state of the system. This parameter is“external”,in the sense that it does not depend on the physical properties of the macromolecule itself, but is determined by the environment(an external electromagnetic field or the phonon subsystem that is in thermal equilibrium with the environment in which the macromolecule is placed,for example). Characteristic soliton parameters expressed by(S,B,p1,p2)are

for symmetric(upper sign)and the antisymmetric(lower sign)soliton solution.
4. Quasiparticle energy spectra
Let us now examine the energetic stability of the soliton solutions. For this purpose,we must find the ground state energy of charge soliton for both obtained solutions and compare them with the energy of the quasi-free charge excitation, i.e.,the energy defined by the functionalℋfrom Eq.(8),but in the absence of the charge–phonon coupling(energy spectra of linear charge excitations).In the case that the ground state energy of solitons is less than the ground state energy of quasi-free charge excitation,we can consider that soliton states are more favorable and they fulfill the conditions for their formation.
4.1. Energy spectra of linear excitations
Firstly, let us find the energy of quasi-free charge states.By settingFq=0,taking the wave functions of the quasi-free particle in the form
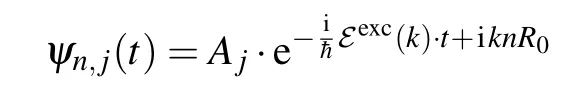
and put them into Eq. (9), we can obtain the system of the linear equations for amplitudesA1andA2as follows:
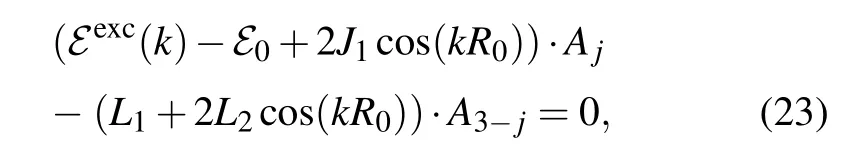
which have a non-trivial solution under the condition that the determinant of the system is equal to zero. From this condition, we can find the energy spectra for quasi-free charge excitations. The energy of the quasi-free particle,normalized by the energy ¯hω0,in(S,B)parameter space becomes
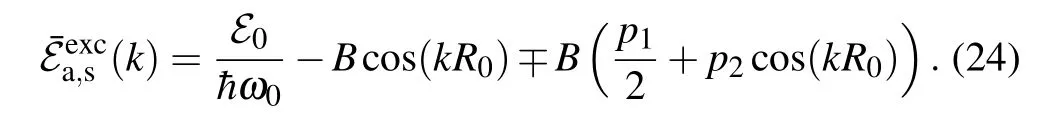
As presented in Fig. 2, the energy spectrum of quasi-free charge splits into two bands separated by the energy gap.
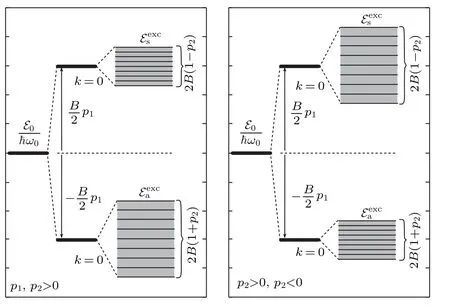
Fig.2. Schematic presentation of the energy bands of the quasi-free charge,for p1 >0, p2 >0(left pane),and for p1 >0, p2 <0(right pane).
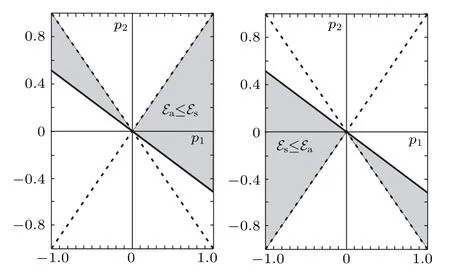
Fig.3. The area in the (p1,p2) parameter space where the antisymmetric states of the free extra-charge are more favorable than the symmetric states (left pane) and the area where the symmetric states of the free extra-charge are more favorable than the antisymmetric states(right pane). One should keep in mind that|L2|≤|L1|,or equivalently,|p2|≤|p1|.
The sign-in Eq.(24)corresponds to the antisymmetric solution(denoted bya),while the sign+corresponds to the symmetric solution(denoted bys). As a consequence,the particle states of linear excitations have the hybrid character: Their states are fully delocalized,and the probability density of the charge is equally distributed on both strands. The width of the energy gap is determined by theL1, while the widths of the energy zones are determined byBand theL2. Because|L2|≤J,the bottoms of the charge energy band for both states are determined byk=0:
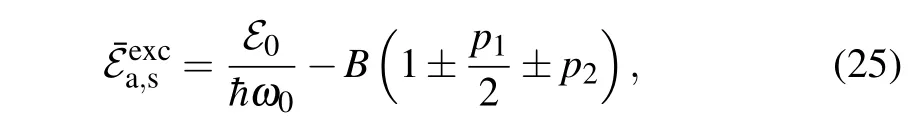
which of these two states is more energy efficient depends on the ratio of the transfer integralsL1andL2. For example,the antisymmetric state is more favorable ifp1+2p2≥0 is fulfilled. This situation in(p1,p2)parametric space is presented in Fig.3.
4.2. Energy spectra of soliton
In order to find the soliton energy,we start from the functional Eq.(8)in the continuum approximation:
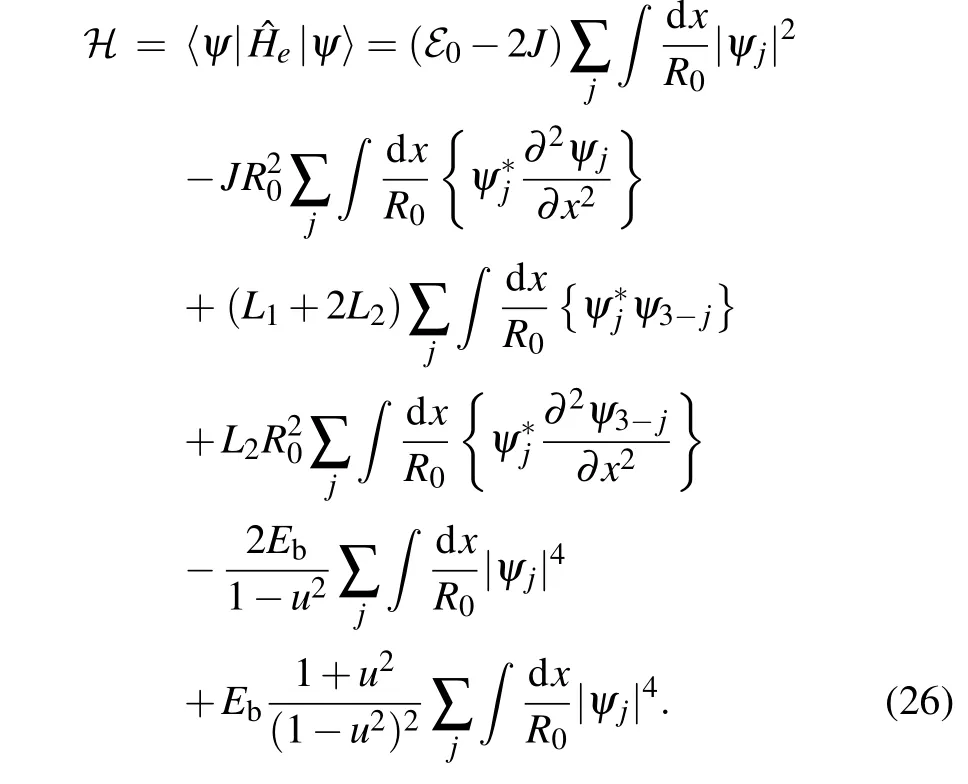
After substituting Eq. (14) into Eq. (26) and using relations amongα,γand(relations in Eqs.(A1)and(A2),from Appendix A),we express Eq.(26)in terms of soliton amplitudesAj:
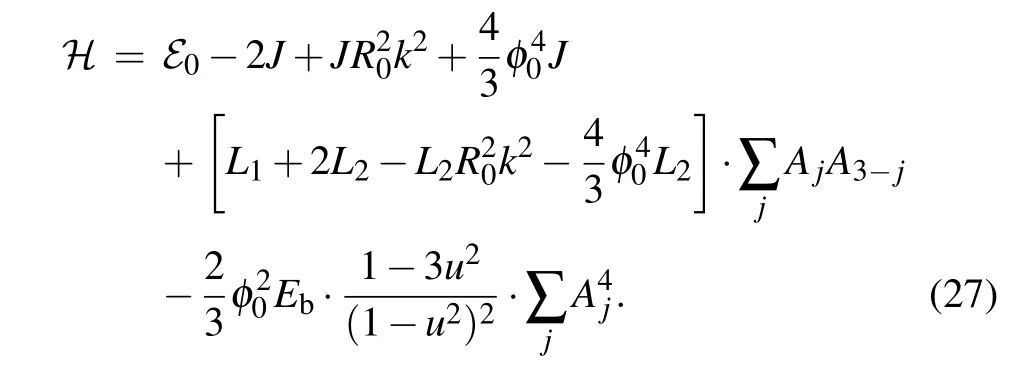
The integrals that appear in Eq. (26) are calculated in Appendix B.Finally,by substituting the values ofAjfor the symmetric and the antisymmetric soliton solutions we obtain the expressions for corresponding soliton energies. In terms ofSandBparameters, soliton energy normalized on the energy¯hω0attains the form
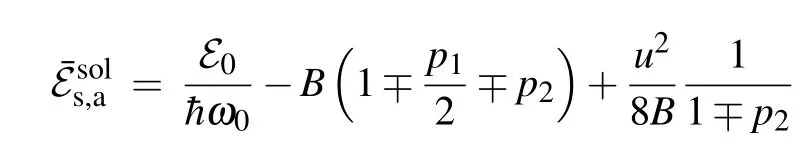
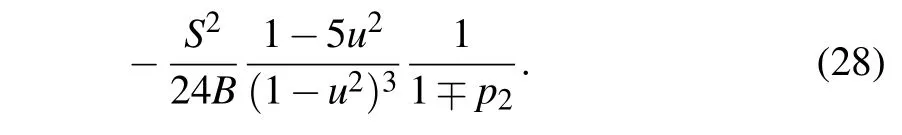
As usual, the upper sign corresponds to the symmetric solution, while the lower one corresponds to the antisymmetric solution. The corresponding ground state energies of soliton solutions are defined byu=0.
5. Analysis of the obtained results
By the analysis of soliton energy,we determine the areas in the(p1,p2)parametric space,which correspond to a particular type of the obtained soliton solutions. After that,we analyze the inertial properties of the obtained soliton solutions,as well as their widths. The analysis of the soliton width allows us to set up an additional criteria on the applicability of the continuum approximation,applied here.
5.1. Energy stability of soliton solutions in parametric space
The obtained relations in Eq.(28)enable us to analyze the energy stability of soliton solutions. By comparing the ground state energy of hybrid soliton solution determined by Eq.(28)with the energy of quasi-free charge Eq.(25),one can see that

is satisfied for all of the values of parametersp1andp2(|p1|,|p2|<1). Consequently, soliton states are more stable(i.e., more favorable)than the states of the quasi-free exciton in the whole(p1,p2)parameter space.

The solution of the inequality (29) in the parametric space(p1,p2)is shown in Fig.4.
The boundary curves separating the two regions in the(p1,p2) parametric space, the region of parameters in which the antisymmetric soliton states are more favorable than the symmetric ones (“AS” region) and the region in which symmetric soliton states are more favorable than antisymmetric ones(“S”region), are shown in Fig.4. Each boundary curve consists of several branches, enumerated by the same number, that corresponds to the particular curve. As we can see,the position and the size of the both regions depend on the values of thep1,p2but also on the ratioS/B. In general,the areap1,p2>0 belongs to “AS” region, while the areap1,p2<0 belongs to“S”region. In the areasp1>0,p2<0 andp1<0,p2>0 there exist both“AS”and“S”regions. For large values of the ratioS/Bthere exists additional “AS” region,forp2~-1 and“S”region forp1~1. Although some estimates indicate that the values ofL1andL2can be of the order ofJ,[10,48]it is often considered that only values for which|p1,2|≪1 have a clear physical meaning. Thus,special attention should be paid to this area of the(p1,p2)parameter space.Here,boundary curves practically correspond to straight lines

as it is presented in the insert picture on the right pane of Fig.4.
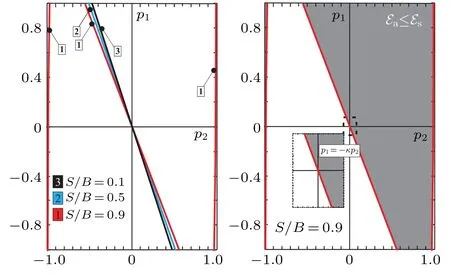
Fig.4. The boundary curves that separate two regions in the (p1,p2)parameter space that correspond to two types of soliton solutions: symmetric and antisymmetric ones. The regions where the antisymmetric soliton states are energetically more favorable than the symmetric soliton states are presented by the shaded area on the right pane. Here,the coefficient κ attains the value κ =1.93.
5.2. Soliton width and the applicability of the continuum approximation
We have already mentioned that soliton solutions of Eq.(13)can be obtained for the“subsonic”soliton case:

This requirement is the consequence of the conditionγ >0 from Eq.(20)and it is the characteristic restriction for soliton solutions of the Davydov type. One should have in mind that the adiabatic polaron approach used here results in the application of a continuous approximation. A somewhat more precise limitation on the usage of the continuum approximation can be obtained taking into consideration of the fact that the larger velocity of the soliton pulse corresponds to a narrower soliton and vice versa[see,e.g.,relations forin Eq.(22)].Namely, in order to apply the continuum approximation, the width of the soliton must be large enough. This imposes an additional condition on the soliton velocity, whose properties can be studied here using the presented model.
If we define the width of the soliton asΔ=ξ2-ξ1,whereφ(ξ1,2)=φ0/D(theDis the parameter that defines what we consider under the“width of the soliton”: forD=2 we consider the half-width of the pulse, for example) our condition becomes

HereΔ/R0is the number of nodes of the structure, covered by the soliton pulse,and theNCis the minimal number of the covered nodes for which continuum approximation is allowed.Although the amplitudeφis interpreted as the distribution of the probability of finding an charged particle along the molecular chain and it can in principle be narrower than the distance between adjacent nodes of macromolecules,previous theoretical studies indicate thatNC≫1.[20,21]Therefore,our next task is to estimate the width of the soliton pulse. Using Eqs. (21)and(22)one can find that the number of nodes covered by the soliton pulse(Δ/R0)is
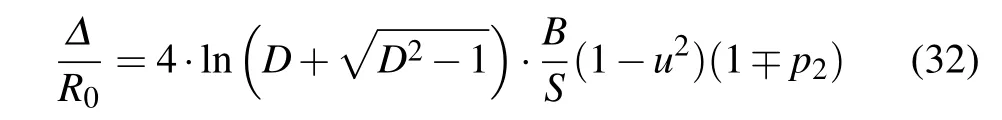
for the symmetric/antisymmetric soliton solutions.It is easy to see that,for all types of solutions,the soliton width decreases by the increasing soliton speed. In addition, it is interesting to remark that the width of the soliton is affected byp2(or equivalently, byL2) directly, but it depends onp1indirectly,through the solution type (symmetric or antisymmetric solution). In the case of the symmetric soliton, the negative values of the parameterp2can significantly increase its width,whenp2~-1. However, increasingp1can yield quite narrow antisymmetric soliton pulse (forp1~1)! Similarly, the extending of the antisymmetric soliton to a large number of macromolecule nodes is possible for positive values ofp2,but whenp1reaches the values close top1~-1 we have narrow symmetric soliton pulse.
Although it does not represent a condition with a strict physical meaning (due to the dependence onDandNCwhich are not physical parameters, but a matter of our agreement),obtained expression(32)together with the requirement Eq.(31)can be used to estimate the upper limit of the soliton velocityumax. It corresponds to the minimal width of the soliton pulse, and consequently, determines the applicability of the continuum approximation in the presented model. From Eqs.(31)and(32)we have
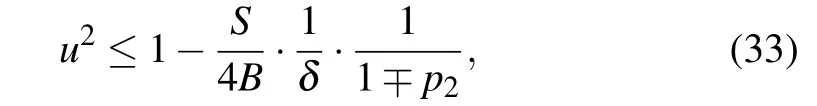
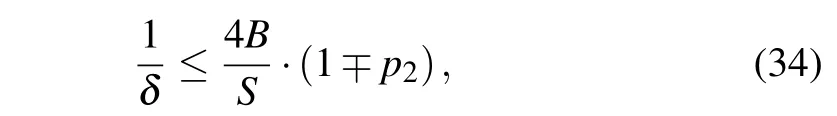
which sets up the condition onNC(depending on the used value ofD)that should be satisfied in continuum approximation.
Let us now estimate the limit values for the number of nodesNCcovered,within the framework of the model we have applied here. It should first be noted that in the case of the symmetric soliton solution, the minimal value of the parameterp2corresponds to the maximal value of the 1-p2, i.e.,to the maximal values ofNCand the soliton velocityu. From Fig. 4 we see that in the case of the symmetric solutions the minimal value of the parameterp2is about-1,while the maximal value isp2≈0.5(for the case ofp1=-1).Using the values of the basic energy parameters,characteristic for the DNA macromolecule,we find that the value of theNCranges to the interval[4, 12](forD=2). Similar result can be obtained for antisymmetric soliton solutions. According to this,continuum approximation is applicable for a relatively small number of the covered nodes. Finally,the solutions of inequality(33)are shown in Fig.5,for the symmetric soliton solutions(left pane)and for the antisymmetric solutions (right pane). For a given value of the parameterp2, all velocities below the curve defined by a certain value of the parameterδcorrespond to those velocities that satisfy the inequality(33).

Fig.5. The boundary values of the soliton velocity, in dependence on p2 and δ. The boundary velocity is defnied by u2 =1- · ·for symmetric(-),and for the antisymmetric(+)soliton solutions. For a given value of the parameter δ,all values of the pairs u2 and p2 that are below the boundary curve satisfy inequality(33).
We notice that small values of the parameterδ(i.e.,those values of the parameterδcorresponding to a soliton pulse that cowers a large number of nodes of macromolecules) correspond to slow solitons.This result is completely in accordance with the properties of Davydov solitons in macromolecular chains. However, as can be seen from Fig. 5, slow solitons are possible only at sufficiently large values of the parameterp2,i.e.,for a sufficiently large overlap of molecular orbitals of diagonally placed opposite nucleic bases.
5.3. Inertial properties of the soliton
To determine the “inertial” properties of the solitons, it is useful to examine the soliton energy in the so-called“nonrelativistic” limes (u ≪1). For that purpose, let us modify relations(28)for the soliton energy as follows:


Here we can define the“soliton mass”as

6. Conclusion
The presented analysis is based on the assumption that the injected extra-charge into two-strand biomolecule, due to its interaction with mechanical oscillations of the structure,is self-trapped and forms an adiabatic polaron state. Such a polaron could(under the presence of an external electrical field,for example) propagate through a macromolecule in the soliton form, maintaining its shape and energy for a long time.Due to the existence of inter-chain transfer integrals(transversalL1and diagonalL2), the amplitudes of the obtained hybrid soliton solutions are distributed on both chains at the same time. We find the hybrid soliton solutions of two types:symmetric and antisymmetric ones,which of obtained soliton solutions is energetically more favorable depends on the values of the basic energy parameters of the considered structure:characteristic phonon energy ¯hω0,polaron binding energyEb,intra-strand TIJ,and inter-strand TI(L1andL2).
Although the soliton picture presented here does not provide the possibility of investigating the process of the interstrand charge migration, it predicts hybrid soliton solutions,which means that the charge can belong to both molecular strands at the same time.This possibility is clear from a physical point of view for sufficiently large values of the ratiosL1/JandL2/J. According to calculations in Ref. [48], the ratiosL1/JandL2/Jfor DNA macromolecule are not so small(they range from 0.1 up to 1,depending on the type of nucleotide).As a consequence,the inter-strand migration of charges cannot be neglected. In addition, our analysis indicates that this migration is possible even for small values of the ratiosL2/JandL1/J: asymmetric forL1>0 andL2>0,as well as the symmetric forL1<0 andL2<0! In other words, the formation of both types of hybrid solitons is possible, regardless of the possible large difference between the values of the inter-strand and intra-strand transfer integrals.
Analysis of the soliton width and its effective mass shows that they depend on the basic energy parameters ¯hω0,Eb,andJ(i.e.,onSandB),in a way that is typical for the soliton solutions of Davydov type. In addition,according to the presented model, these soliton parameters explicitly depend onL2, but onL1they depend implicitly! Additional analysis of the mutual influence of the soliton velocity and its width shows that narrower solitons can propagate by a higher velocity, but the intensity of this velocity decreases with increasingL2! Consequently, the diagonal inter-strand TIL2plays an interesting role in the model,explicitly influencing numerous soliton parameters, whileL1influences mainly on the charge energy spectra(i.e.,on the width of the energy gap that separates the zones of the hybrid soliton state).However,one should have in mind that the values of these parameters can depend on many factors:ambient temperature,relative position of structural elements or their spatial orientation,for example.
For hybrid soliton solutions,the probability of finding an charged particle in a biomolecule consisting of two molecular chains is equal to both chains. Therefore, any change in the structure of biomolecules (such as cleavage of biomolecule or a significant increase in the distance between its chains)can significantly change the properties of induced solitons.For example, in regions of DNA that have a significant number of thymine-adenine nucleotide pairs, thermal fluctuations can locally break weak hydrogen bonds. In this way, transient breathing bubbles can be formed locally,which will significantly influence to the charge propagation in this area of biomolecule.
The presented model also does not take into account some other effects that appear in real biomolecules such as nonlinear H-bond dynamics,the helical geometry,or the influence of the back-bone which exists in the DNA case,for example. Nevertheless,it provides a clear picture of the self-trapping process of the injected extra-charge in double strand macromolecular structure, and the basic properties of the eventually formed soliton excitation. To improve this picture,in the next stages,it is possible to include the nonlinear interaction between two adjacent structure elements belonging to the different strands.Also,one of the future tasks should be the investigation of the influence of the thermal bath on the soliton solutions for the injected extra charge.
Appendix A:Two very useful relations for soliton amplitude φ0
In Eq. (21) we have relation=2α/γconnecting the soliton amplitude with the ratio of the parametersαandγ.Using the normalization condition for the envelope function,it is possible to express the soliton amplitudeφ0either throughαorγ. Starting from normalization condition for the envelope functionφ2(ξ)=1 and substitutingφ(ξ) from Eq.(21),one can obtain
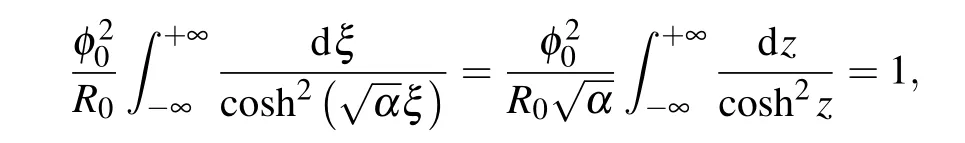
wherez=. Thus,we express the envelope amplitudeφ0through the parameterα:


Appendix B: Important integrals appearing in our calculations
To obtain Eq. (27), we must first calculate the following integrals:
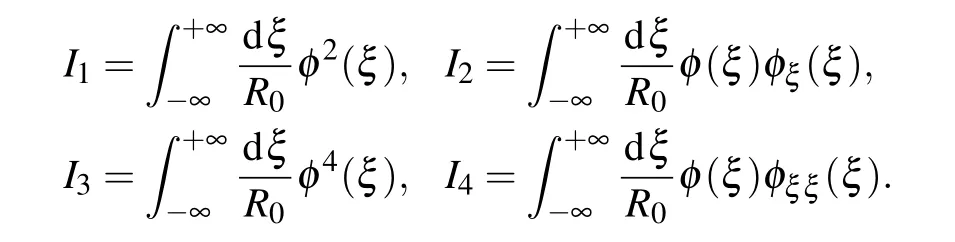
Let us start with the integralI1. According to the normalization condition forφ(ξ)Eq.(16),we have

The integralI2can be transformed as follows:
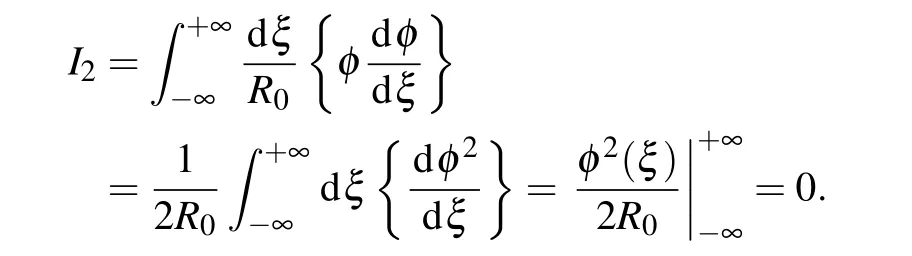
Here we have used the initial conditions for the envelope function in Eqs.(15a)and(15a). The integralI3can be calculated using the explicit form of the envelope functionφ(ξ)Eq.(21).It is not difficult to find

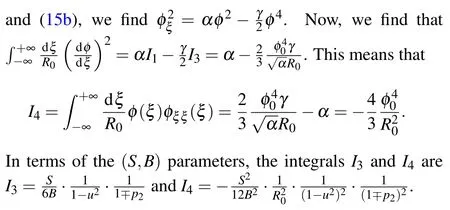
Acknowledgements
Project supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia,the Ministry of Science and Higher Education of the Russian Federation in the framework of Increase Competitiveness Program of NUST“MISiS”(Grant No.K2-2019-010),implemented by a governmental decree dated 16th of March 2013,N 211,and by the Project within the Cooperation Agreement between the JINR, Dubna, Russian Federation and Ministry of Education and Science of the Republic of Serbia.
杂志排行
Chinese Physics B的其它文章
- The coupled deep neural networks for coupling of the Stokes and Darcy–Forchheimer problems
- Anomalous diffusion in branched elliptical structure
- Inhibitory effect induced by fractional Gaussian noise in neuronal system
- Enhancement of electron–positron pairs in combined potential wells with linear chirp frequency
- Enhancement of charging performance of quantum battery via quantum coherence of bath
- Improving the teleportation of quantum Fisher information under non-Markovian environment
