Inhibitory effect induced by fractional Gaussian noise in neuronal system
2023-02-20ZhiKunLi李智坤andDongXiLi李东喜
Zhi-Kun Li(李智坤) and Dong-Xi Li(李东喜)
1College of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China
2College of Data Science,Taiyuan University of Technology,Taiyuan 030024,China
Keywords: inhibitory effect,inverse stochastic resonance,fractional Gaussian noise,neuronal system
1. Introduction
Nervous system is a typical complex nonlinear system,which is mainly responsible for regulating the activities of various organs in the body. As the organism is often in a random fluctuation of the external environment,when the external stimulus acts on the nervous system, the system can respond to the outside world in time and interact with the surrounding environment, which is usually described in the form of noise or random force in physics. Neurons,the basic unit of the nervous system,can transmit information by firing.The firing behavior of neurons is affected by a variety of random factors.In recent years,many scholars have carried out a large number of theoretical and experimental research on the firing activity of neurons in nonlinear systems. The research shows that noise plays a major role. On the one hand,noise has a great promoting effect, such as noise-induced phase transition,[1,2]coherent resonance and stochastic resonance,[3–7]where stochastic resonance can be used to enhance the signal of waves[8]and amplify the spectrum.[9]On the other hand,noise-induced inverse stochastic resonance (ISR)[10–13]is found. Since noise is widespread in the nervous system, it also has a significant impact on the efficient transmission of information in the system.Therefore,studying the influence of noise on the dynamic behavior of nervous system has important theoretical significance and wide application value, which provides new ideas for people to explain many complex behaviors in physical,biological,chemical and social systems.
At present, there have been relevant research results on the effect of noise on neurons,especially on the phenomenon of inverse stochastic resonance. The earliest study on ISR was when studying the effect of noise on neuronsin vitroby Paydarfaret al.,[14]and they observed that noise could inhibit the activity of pacemaker, and low noise intensity could induce the transition between resting state and continuous discharge behavior. Then, Gutkinet al.[15]found that Gaussian white noise inhibited the firing level of neurons. Guoet al.[16]confirmed that color noise was more powerful inhibitory effect than white noise.Gutkin,Tuckwell and Jost[17]considered the inhibitory effect of noise on the discharge of individual neurons,and found that there was a minimum discharge spike,in a range of input current close to triggering a rhythmic discharge.Tuckwell and Jost[18]explained this phenomenon of minimum emissivity ISR in Hodgkin–Huxley system as the noise level increased. Uzuntarla[19–21]observed static synapses and channel noise could induce an inverse stochastic resonance of the neuronal model, and found that when the noise level was optimal, the average peak activity of the single neuron model appeared the minimum value.Liet al.[22,23]successively studied the ISR phenomenon under non-Gaussian noise and Levy noise driven neuronal models,and found that the noise parameters can minimize the average firing rate. Luet al.[24]analyzed ISR phenomena caused by Gaussian and non-Gaussian color noise in the neural network respectively, and the result showed that the ISR phenomenon is caused by Gaussian thermal noise.
Up to now, the occurrence of ISR is mainly studied under the background of ideal Gaussian-type white or color noise. These noises are produced under standard Brownian motion(Bm), but natural behavior is complex, there are a lot of random fluctuation or long time memory noise, and random noise environment plays an important role in the study of biodynamics.[25]Standard Bm to simulate the noise emitted by real behavior of neuron discharge has some limitations,so it is necessary to carry out non-standard Bm,i.e.,fractional Bm(fBm). Compared with the classical Bm with independent increments,fBm has long distance and strong space–time correlation. In recent years,fBm has become increasingly mature in theoretical research. It has become a powerful tool to study the actual behavior of biological,physical and other systems.
The aim of this paper is to explore inhibitory effect induced by fractional Gaussian noise on neuronal firing patterns.Using fractional Gaussian noise to simulate random small perturbations of external environment, firing pattern of neurons is observed and discussed. The innovation of this paper is to study the inhibitory effect driven by fractional Gaussian noise through dynamic measurement, such as time series analysis,average discharge rate and inter-spike intervals. We will focus on the effect of noise parameters and input current on the neuronal spike discharge behavior,especially on the phenomenon of inhibitory effect, i.e., inverse stochastic resonance. Meanwhile,revealing the mechanism of inhibiting the firing of neurons by fractional Gaussian noise lays a solid foundation for better studying the internal activity of biological organisms.
The structure of this paper is as follows. In Section 2,the classical Hodgkin–Huxley (H–H) model and fGn are explicitly introduced. In Section 3,the inhibitory effects of different noise parameters(noise intensity and Hurst index)on neuron firing are studied. In Section 4,ISR is confirmed in H–H neuron model induced by fractional Gaussian noise by calculating the average discharge rate. In Section 5, in order to further explain that fractional Gaussian noise can produce ISR, the concept of inter-spike intervals(ISIs)distribution histogram is introduced,and ISR phenomenon is verified by the change of ISIs. Finally,the above conclusions are summarized and their biological significance is discussed in Section 6.
2. Model and fractional Gaussian noise
2.1. H–H neuron model
In 1952,British physiologists and biophysicists Hodgkin and Huxley[26]used the laboratory to determine the cell membrane of squid giant axons, and found that the nerve membrane had membrane capacitance and conductance as well as membrane potential and time ion channels related to conductance. In order to explain the mechanism of action potential generation and propagation, the following nonlinear ordinary differential equations,[27–29]known as H–H model, were established:

In system(1),when the particle is in the correct position,mis the activation variable of sodium ion,which represents the average activation probability of sodium ion channel.nrepresents the probability of activating the potassium channel, andhis the inactivation variable of sodium ion, representing the average probability of inactivation of the sodium ion channel.αnrepresents the velocity constant of potassium ion channel from closing state to an open state,βnis the velocity constant of potassium ion channel from opening state to a close state.The control variablesαm,αn,αh,βm,βn, andβhsatisfy the following equations:

2.2. Fractional Gaussian noise
The fractional Gaussian noise was first introduced by Mandelbrot and Van Ness[30]for simulating stochastic fractal processes. From the perspective of statistical physics,fGn is aE-dimensional random vector field defined ind-dimensional space.dandEcorrespond to spatial dimension and spin dimension respectively in the theory of critical phenomena in statistical physics. Before introducing fractional Gaussian noise, the concept and properties of fractional Bm are firstly given below.
2.2.1. Fractional Brownian motion
Mandelbrot and Van Ness[30]first proposed the term fractional Bm,which was obtained by random integration of standard Bm. Fractional Bm(fBm)has significant similarity and differences compared to the standard Bm,they both have stable increments in common,and the difference is that the fBm increment has strong long-range correlation or long memory,while the Bm has independent increments.
TheBH(0)(t ≥0) is a real-valued and non-stationary Gaussian process. Among themBH(0)=0,the mean is zero,and the covariance function is
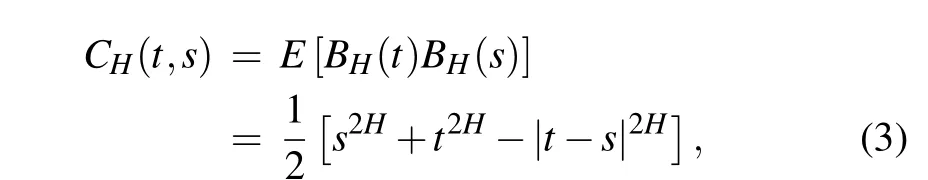
whereHis the Hurst index,H ∈(0,1),and theBH(t)is called fBm. In particular, the fBm decays to Bm whenH= 0.5.Some common properties of fBm are given below.[29,31–36]
Property 1fBm is self-similar,

That is,theBH(at)andBH(t)have the same finite-dimensional distribution.
Property 2The increment of fBm is stationary.
For random variablesBH(t) andBH(s), ift >s, the distribution ofBH(t)-BH(s) is independent of the starting and ending moments,only depends on the time lagt-s.
Property 3The increments of Property 2 are correlated at non-overlapping intervals.Fort >s ≥u >v,

Property 4When Hurst indexH ∈(0.5,1), fBm shows long range memory.
Consider the incremental processZt=BH(t)-BH(t-1),t=1,2...,
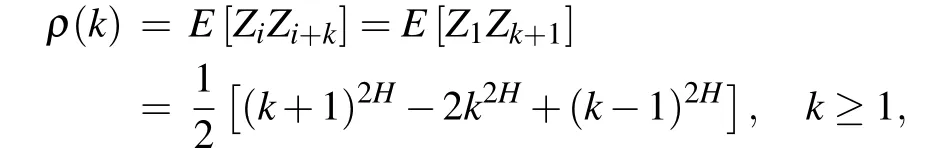
Property 5B1/2is Brownian motion.
WhenH=0.5,

sinceBHis a Gaussian process with zero mean value, andBH(0)=0,soB1/2is Bm.
Figure 1 simulates sample paths of fBm with different Hurst index values. Given the self-similarity of the fBm, its sample path is fractal in statistical significance and is constant and invariant on any time scale. Through observation,we can see that the sample path is smoother and extends farther back as theHcontinuously increases. This is because the negative correlation(resistance persistence)makes fBm show high variability whenH <0.5 (H=0.3), while the sample path is smoother due to positive correlation(persistence)whenH >0.5(H=0.7).

Fig.1. Fractional Brownian motion BH(t) with different Hurst index,H takes 0.3,0.5,and 0.7.
2.2.2. Generation of fractional Gaussian noise
Fractional Gaussian noise is generated by the fBm. Comparing the Gaussian white noise,as a formal derivative of the Bm,fractional Gaussian noiseGH(t)is interpreted as the formal derivative of fBm,[37]that is,

It has stationarity, self-similarity, and long-range correlations. It is a fat-tailed autocorrelation function, no longer Markovian except that the probability structure is still Gaussian,but exhibits some long correlations. In recent years with studies on fractional Gaussian noise, various methods such as the Hosking method,[38]the Cholesky method[39]and random midpoint displacement[40]had been proposed to generate corresponding random numbers. Here we employ a random midpoint displacement method to simulate fractional Gaussian noise. Kouet successfully explained the sub-diffusion of individual protein molecules by introducing the fGn into the generalized Langevin equation.[41]Fractional Gaussian noise complete self-similarity was frequently used to model many subject phenomena in computer network models,[42,43]signal processing,[44,45]economic domain.[46,47]
Below we give the spectral density of fGn under the Hurst index corresponding to Fig.1. The results are shown in Fig.2,and it can be found that in these three cases,there are obvious differences in their frequency distribution.WhenHis less than 0.5(H=0.3),the amplitude value rises monotonously at first and gradually become stable,and the high-frequency component is dominant in the spectral density. WhenH=0.5, the fBm will attenuate to the standard Bm,and the corresponding fGn will also become Gaussian noise correspondingly. The amplitude value fluctuates up and down within a certain width,and the corresponding spectral density is evenly distributed.WhenHis greater than 0.5(H=0.7),the amplitude value first drops slowly and monotonically and then stabilizes,where the low-frequency component occupies a larger proportion.
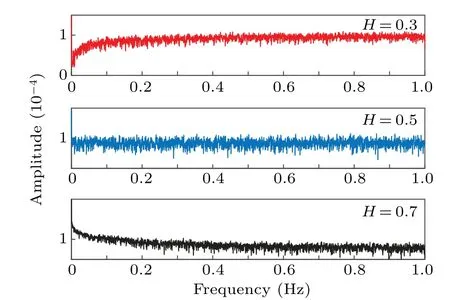
Fig.2. Spectral density of fractional Gaussian noise GH(t)with different Hurst index,H takes 0.3,0.5,0.7.
3. Time series of neuron induced by fGn
To simulate the numerical solution of Eq.(1),the Euler–Maruyama algorithm[48]is used. The initial condition is(V(0),m(0),h(0),n(0)) = (0,0.006,0.6,0.35). In order to more clearly display the influence of noise on the discharge mode in the H–H model, the potential changes of neurons in the first 300ms are only shown here.
3.1. Effect of noise intensity on neuron discharge
Figure 3 shows a time-course plot of neuronal firing at different noise intensities.First of all,when the noise intensity is small relatively(D=0.1),there is little inhibitory effect on neuronal firing. When the noise intensity increases toD=5,it is obvious that the number of spikes of neurons decreases sharply,indicating that when the noise intensity increases,fGn will have a strong inhibitory effect on the discharge of neurons.When the value of the noise intensity continues to increase toD=9,it can be found that neurons return to full firing mode and inhibition disappears. As theDvalue increases,the membrane potential in neurons successively experiences complete firing,firing inhibition,and complete firing. We can conclude that the noise intensity is too large or too small to produce no significant inhibitory effect on neuronal firing,while the noise intensity of the fractional Gaussian noise can have a significant inhibitory effect on the neuronal firing levels when theDtakes the appropriate value.
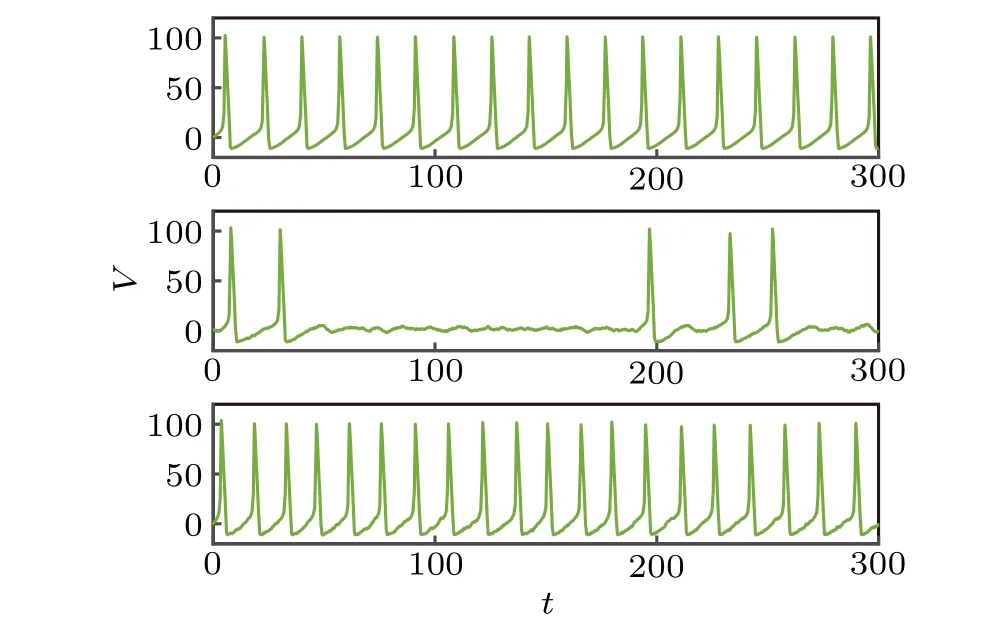
Fig.3.Time series plots of the neuronal model at different noise intensity,where external current I=7 and Hurst index H=0.6,D takes 0.1,5,9.
3.2. Effect of Hurst index on neuron discharge
Next, in order to further show the effect of Hurst index on neuron discharge, we plot the time series diagram varies with Hurst index in Fig.4. The result shows that with the increase ofH, the number of neuron discharge peaks will first decrease,and then increase to the complete discharge state almost the same as before. Similarly,we also have a conclusion similar to the above: only when the Hurst index is within an appropriate range,can the neuron discharge be inhibited.
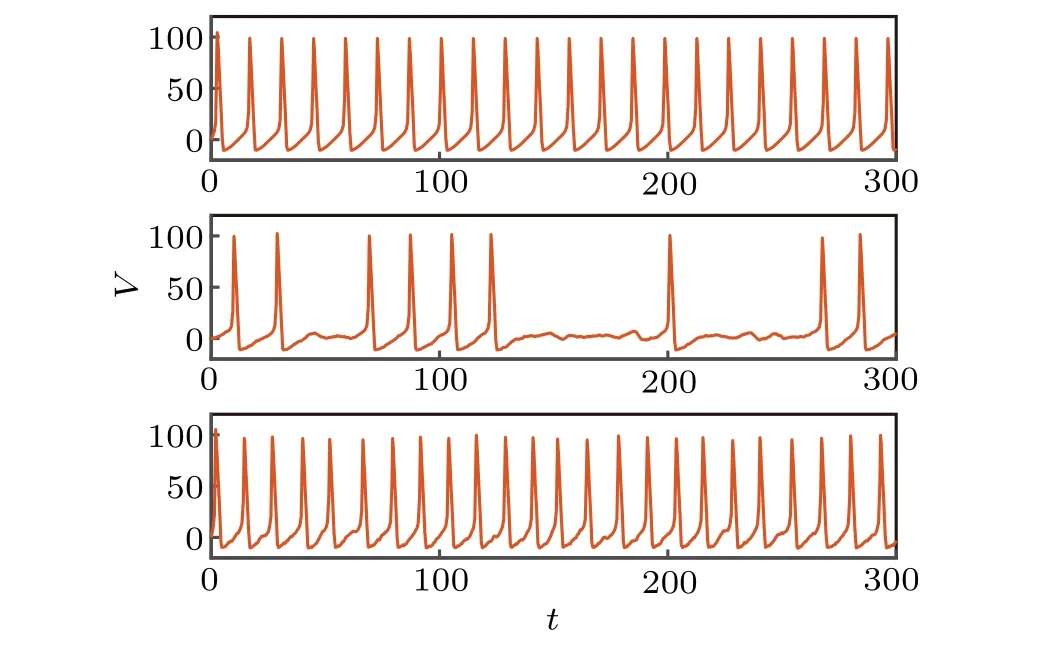
Fig.4. Time series plots of the neuronal model at different Hurst index,where external current I=7 and noise intensity D=0.6, H takes 0.3,0.7,0.9.
Above, we discuss the influence of the two parameters of fractional Gaussian noise on the firing mode of neuron model respectively, and finally reach a consistent conclusion,the introduction of noise break the original regular firing mode of neuron. The random factors of fractional Gaussian noise(noise intensity and Hurst index)can inhibit the firing of neurons. And the value of noise parameters should not be too small or too large,within a certain range,the discharge of neurons can be effectively suppressed,that is,there will be inverse stochastic resonance phenomenon.
4. Inverse stochastic resonance induced by fGn
To quantify the inhibitory effect of fractional Gaussian noise on neurons, we introduce the concept of average discharge rate to measure it,and numerically express the effect of fractional Gaussian noise on neuron discharge behavior,which is a common method to measure the level of inverse stochastic resonance. We systematically study the effect of external input current intensity and fractional Gaussian noise on neuron model. It is stipulated that when the membrane potential is greater than 50 mV, the peak value is recorded. The formula of the average discharge rate[16]is

whereNspikes,iindicates the number of spikes in thei-th numerical simulation,Mis total number of simulations andtis total time.M=300 andt=600 ms are used for simulations in this paper.
4.1. Average discharge rate with noise intensity
Figure 5 shows the dependence of the average discharge rate with the noise intensity. As shown in Fig.5(a),the influence of noise intensityDof different Hurst indexHon the average discharge rateRis considered. WhenHis less than 0.5(H=0.3), the average discharge rate curve decreases slowly first and then rises slowly, which indicates that the inhibitory effect is not obvious. WhenH=0.5,Rdecreases rapidly first,and then increases rapidly,and this observation means that the inhibition of fGn on neurons is enhanced. WhenHis greater than 0.5(H=0.7),the inhibitory effect of noise is further enhanced, and the value ofRdecreases sharply first, and then rises fast. When the value ofHcontinues to increase to 0.9,the value ofRfirst drops slightly and then rises rapidly, and the inhibitory phenomenon weakens obviously. Keep on increasing the value ofH, the inhibitory effect will even disappear. Therefore, it can be concluded that when the current is a constant near the critical threshold range, and the value of Hurst indexHis changed from 0.1 to 0.9,Rwill first decrease and then increase with noise intensity, in other words, the inhibitory effect of noise on neuron discharge will first enhance and then weaken.Thus,within a certain range,the Hurst index is more potent against neuronal firing.
Next, exhibiting the neuronal firing affected by external current. As shown in Fig. 5(b), the change of average discharge rate under different noise intensity is studied by changing different current values. It can be found that when the current value is 5.5,with the increase of noise intensityD,the average discharge rate curve presents a slow and monotonous trend.When the current value increases toI=6.6,the average discharge rateRdecreases first and then increases,this implies inhibitory effect appears. When the value ofIcontinues to increase to 8,the phenomenon of inhibition still exist. When the value of currentIis large(I=9.5),the average discharge rate decreases slowly at first and then rises slowly, the inhibition effect disappears gradually. This reveals that the average discharge rate is highly sensitive to the current intensity,a small change in the current intensity is enough to cause a great difference in the discharge inhibitory effect. We can conclude that within the threshold range of current intensity,the average discharge rate curve decreases first and then increases with the increase of noise intensity. Besides,it can be very clear that a significant phenomenon of inhibition occurs.
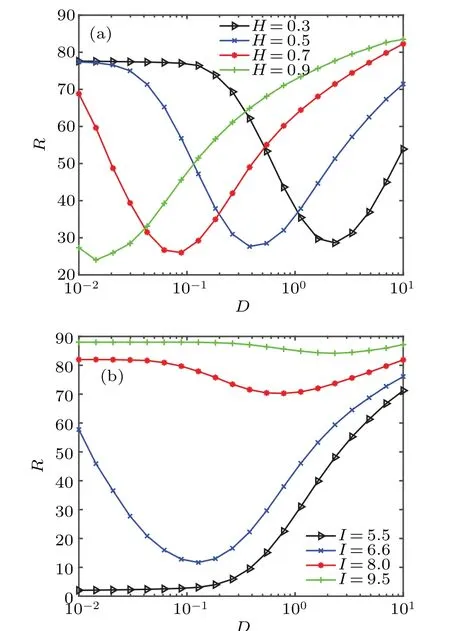
Fig.5. The average firing rate R varies with noise intensity D at different parameters. (a)Fix the external current as I=7,Hurst index H makes 0.3, 0.5, 0.7, 0.9. (b) Fix the Hurst index as H =0.6, external current I makes 5.5,6.6,8,9.5.
4.2. Average discharge rate with Hurst index
Figure 6 shows the dependence of the average discharge rate with the Hurst index. As shown in Fig. 6(a), the change of average firing rate of neurons with Hurst index under different noise intensityDis considered. When the noise intensity is small(D=0.1 andD=1), there is a significant minimum average discharge rate. Continue to increase the noise intensity (D=4), the average discharge decreases slowly at first,then increases rapidly, and the inhibition gradually weakens.When the value ofDincreases to 7.5,the value ofRdecreases slowly at first, then increases sharply with the increase ofH,and the inhibition effect almost disappears. It can be seen that the suppression effect is more significant under the low noise intensity.

Fig.6. Average firing rate R varies with the Hurst index H under different parameters. (a)External current I=7,noise intensity D makes 0.1,1,4,7.5. (b)Noise intensity D=0.6,external current I makes 5.5,6.6,8,9.5.
To take into account the effects of different external currents on neuronal discharge. Figure 6(b) shows theR–Hcurves corresponding to the different currents. When the current value is 5.5, the average discharge rate curve shows a slow-growing trend,there is no inhibition occurs. With the increase of the current value,whenI=6.6,an inhibitory effect appears. The value ofIcontinues to increase to 8. Despite the existence of inhibitory effect, the decrease ofRvalue is significantly smaller than that ofI=6.6, indicating that with the increase ofI, the inhibitory effect of noise on neurons is further weakens. When the current value increases toI=9.5,the inverse inhibitory effect disappears. According to the observation above, we can conclude that under the condition of constant noise intensity and current within the threshold range,the inhibitory effect will first enhances and then gradually disappears with the increase ofI.
Finally,in order to observe the influence of noise parameters on average discharge rate more intuitively, the average discharge rateRwith Hurst indexHand noise intensityDis given in Fig.7(a). It can be seen from the cross section ofD,when the value range of noise intensity is small,the inhibition effect is more obvious.With the increase of noise intensity,the inhibitory effect on neuron firing gradually disappears,which is consistent with the result in the figure above. On the other hand,along the cross section ofH,the inhibition effect is not obvious whenH <0.5. AsHincreases to 0.5,the inverse inhibition effect becomes clearer, but whenHincreases to 0.9,inhibition effect disappears. This indicates thatHhas a more significant inhibition of neuronal firing in a certain range.This is consistent with previously confirmed results. In conclusion, with the decrease of noise intensity, noise has a more significant impact on neuron discharge,while Hurst index can only effectively inhibit neuron discharge behavior in a certain range.

Fig.7. (a) Average discharge rate R with noise intensity D and Hurst index H. (b)Average discharge rate R with Hurst index H and current intensity I.
In addition, external input current can affect firing mode of neurons. Then we simulate the average discharge rateRregarding Hurst indexHand currentI, as shown in Fig. 7(b).From the perspective of the cross section ofI, when the current is close to the threshold, it has obvious inhibition effect,and the inhibition phenomenon decreases or even disappears beyond the threshold. However,whenHis in the appropriate value range,with the continuous increase of current,the average discharge rate will first decrease slowly and then increase rapidly.
5. Inter-spike intervals induced by fGn
The most common way to study the firing patterns of neurons is to measure the distance between different firing sequences. The advantage of this method is that there is no unit scale and subjective factors can be ignored, which makes the results more objective and improves the visibility of information between discharge sequences. In order to verify the above series of conclusions about the inhibitory effect of fGn on neurons. In this paper,the concept of inter pulse interval(ISIs)is introduced, which represents the time interval between adjacent peaks of a neuron. By comparing the changes in the number of peak discharges generated in a given period of time,the suppression effect under different noise parameters can be obtained. Finally,we can directly reflect the existence of inhibition effect through the histogram of peak to peak distribution.

Fig.8. (a) Histogram of peak-to-peak intervals under different Hurst index,I=7 and D=0.6 are fixed,H takes 0.3,0.7,0.8. (b)Histograms of peak-to-peak intervals at different noise intensity,I=7 and H=0.6 are fixed,D takes 0.1,5,8.
Figure 8(a) is the peak-to-peak period histogram under different Hurst indices. With the increase ofH,the number of neuron discharge peaks in the same peak decreases first and then increases. This is consistent with the previous conclusion of the corresponding time history diagram under differentH.By using a similar method,when Hurst exponentH=0.6,the corresponding peak-peak cycle histogram ofD=0.1,D=5 andD=8 are shown in Fig 8(b), respectively. The number of discharge peak decreases first and then increases with the increase ofD. Combined with these two figures, it can also be seen that when noise parameters are small,neurons are in a state of complete discharge,with a large number of discharge tips and a concentrated peak–peak cycle distribution. With the increase of noise parameters,the number of tips decreases significantly and the corresponding distribution becomes more dispersed. As the noise parameters increase, the number of peaks almost returns to its previous level and the distribution becomes more concentrated. At this point,the neuron reaches a state of almost complete discharge. These results indicate that the addition of noise breaks the original rhythmic firing mechanism of neurons and inhibits the firing of neurons.
6. Conclusions
The inhibitory effect of fractional Gaussian noise on neuron firing is studied. Firstly, the Hodgkin–Huxley neuron model and fractional Gaussian noise are presented. Secondly,the effect of noise parameters on neuron firing under fractional Gaussian noise is studied. We observe that fractional Gaussian noise can inhibit neuron firing in a certain range of noise parameters,and give the corresponding neuron firing time series diagram. Next, we take the average discharge rate as the measurement value of neuron discharge, and find that with the increase of noise intensity and Hurst index, the average discharge rate presents a minimum value, which is ISR phenomenon. The results show that when the input current intensityIreaches the critical threshold,the Hurst index and noise intensity can induce ISR.Finally,in order to further prove the inhibitory effect of fractional Gaussian noise on neuron firing, we introduce the concept of peak interval. The results show that with the increase of Hurst index and noise intensity,the number of inter peak intervals decreases first and then increases. In conclusion,the Hurst exponent and noise intensity of fractional Gaussian noise can induce ISR phenomenon in neuron system. Compared with ISR caused by other kinds of Gaussian-type noise, noise intensity and Hurst index of fractional Gaussian noise can cause ISR. The main difference is that the Hurst index of fractional Gaussian noise could express a long range correlation, which can better describe the randomness in the real world.
In this paper, the Hodgkin–Huxley model is applied to a single neuron to study the inhibitory effect of fractional Gaussian noise on neuron discharge,namely,the emergence of ISR.Our results can also be further extended to neural networks.Because noise inevitably appears in biological system, it can not only produce positive effects,[49]but also hinder the dynamic behavior of biological system. A better understanding of noise-induced ISR helps to discover complex and interesting dynamic discharge behaviors in the nervous system.Fractional Gaussian noise is more representative of the disturbance. Fractional gaussian noise is more common in practical applications and can simulate random interference. Fractional gaussian noise can trigger the discharge activity of biological system. ISR can be caused by fractional Gaussian noise.And,some results are obtained,which are different from other Gaussian or non-Gaussian noises. In addition,the influence of fractional Gaussian noise on biodynamic behavior and its application deserves to be further explored. Due to the complex structure of biological system, its functional significance and biological mechanism remain to be explored.
In addition, the functional implications of ISR are still unclear,more important roles will emerge in the future. Many studies have investigated many functional roles of ISR. For example, ISR may play an important role in shortening the cycle of abnormal working memory.[50]In the process ofinvitropreparation of purkinje cells from rat brain slices,[51]it was found that ISR could be used to switch between different operating mechanisms according to input current. ISR was also found in nematic liquid crystal.[52]At present,the mechanism of inverse stochastic resonance is widely used in biomedical and many areas,so it is very promising to make good use of its unique mechanism and play an active role to reveal the internal information transmission mechanism of the nervous system,promote the progress of biomedicine,explore the new applications in the field of economic and financial and others.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No. 11402157) and Applied Basic Research Programs of Shanxi Province, China (Grant No.201901D111086).
杂志排行
Chinese Physics B的其它文章
- LAMOST medium-resolution spectroscopic survey of binarity and exotic star(LAMOST-MRS-B):Observation strategy and target selection
- Vertex centrality of complex networks based on joint nonnegative matrix factorization and graph embedding
- A novel lattice model integrating the cooperative deviation of density and optimal flux under V2X environment
- Effect of a static pedestrian as an exit obstacle on evacuation
- Chiral lateral optical force near plasmonic ring induced by Laguerre–Gaussian beam
- Adsorption dynamics of double-stranded DNA on a graphene oxide surface with both large unoxidized and oxidized regions
