Firing activities in a fractional-order Hindmarsh–Rose neuron with multistable memristor as autapse
2023-02-20ZhiJunLi李志军WenQiangXie谢文强JinFangZeng曾金芳andYiChengZeng曾以成
Zhi-Jun Li(李志军), Wen-Qiang Xie(谢文强), Jin-Fang Zeng(曾金芳), and Yi-Cheng Zeng(曾以成)
1School of Automation and Electronic Information,Xiangtan University,Xiangtan 411105,China
2School of Physics and Optoelectronics,Xiangtan University,Xiangtan 411105,China
Keywords: fractional-order,multistable,neuron,firing,locally-active memristor
1. Introduction
As an important basic unit of the nervous system, biological neuron has rich and complex firing activities. In order to study the firing patterns and operating mechanisms of the biological neurons, many neuron models have been proposed based on the experimental data of electrophysiology in recent years. The classic paradigm is the Hodgkin Huxley (HH)model[1]proposed by British physiologist and biophysicist Hodgkin and Huxley in 1952. Subsequently,some simplified models,such as Hindmarsh–Rose(HR),[2]FitzHugh–Nagumo(FHN),[3]Izhikevich,[4]and Morris–Lecar (ML) models[5]were derived from the classic HH model. After that,complex firing activities, which are similar to the dynamics of the biological neurons,have been uncovered in these classical neuron models.[6–10]Synapses are key parts of functional connection and information transmission between neurons. There is a special type of synaptic structure called autapse, which is the synaptic connection formed by axons of neuron and its own dendrites or cell body. Activation of autapse can enhance the reactivity of neurons and promote cluster release, which plays a vital role in neuronal signal processing,[11–13]so how to model the function of biological autapse has become an urgent problem. Memristor[14,15]devices are considered to be the optimal solution to simulate biological synapses due to their good biomimetic characteristics[16,17]such as low power consumption,nonvolatile,plasticity and nano size. Thus,considering memristors as synapses or autapses to construct nervous systems has become a hot topic in the field of neurodynamics. For example, Wanget al. proposed a cable neural network with autapse connection,and found that under certain external conditions, autapse can further enhance the adaptive ability to external stimuli.[18]Wanget al. studied the influence of autapse on the firing mode and dynamic characteristic of the HR neuron, and revealed that the firing mode of neurons can be changed by adjusting the autaptic intensity and the time-delay.[19]References[20–22]also studied the collective dynamic behaviors of multiple neurons which are coupled by memristor-based autapses.
As we all know, fractional calculus is an extension of integral calculus, which can accurately depict the long memory and hereditary properties of dynamical process in the real world. In recent years, fractional calculus has been widely used in physics, biomedicine, biophysics and other fields.[23–25]In neurodynamics, fractional differentiation can predict stimuli, and improve information processing ability.[26]Therefore, the fractional-order neuron models can mimic the electrical activity of biological neuron more reasonably. In Ref.[27],a complex biological system was modeled by fractional operation calculus in a direct and rigorous manner, accurately describing the propagation of subthreshold nerves. In Ref. [26], it was found that the multi-time scale adaptation of single rat neocortical pyramidal neurons could be well simulated by fractional calculus. The study on dynamics of fractional-order neurons has attracted extensive attention. Yunet al. found hidden periodic and chaotic bursting in the fractional-order HR neuron model by fast–slow analysis.[28]Alidoustiet al. revealed the different firing patterns of the fractional-order FNH neuron model and the related bifurcation mechanisms were also explored.[29]The dynamics and chaotic synchronization of two fractional-order HR neurons with time delay under electromagnetic radiation were explored by Menget al.[30]Their research results show that the fractional-order has an important influence on the firing patterns. Furthermore,the effects of fractional-order on synchronization of neuronal networks under different external conditions were reported in Refs.[21–33].
Local activity is the origin of complexity.[34]In 2014,Chua proposed the first locally-active memristor.[35]Compared with ideal memristors, the locally-active memristors have more complex nonlinear dynamic characteristics.[36–40]The multi-stability characteristic of the locally-active memristor[41]makes it a good means to study the firing behavior of neurons. Thus, the locally-active memristor based neurons and neuronal networks have been extensively studied in recent years. For example, Liet al. constructed a bistable neural network based on the locally-active memristor, and revealed the switching and bifurcation behaviors of firing patterns in the neural network.[42]Linet al. developed an HR neural network based on a tristable locally-active memristor,and found that the proposed neural network produces three multi-stable phenomena with four different firing patterns simultaneously.[43]A model of HR neuron with four-stable locally-active memristor as self-synapses was proposed by Liet al. and they found that four stable firing patterns in the proposed neuron can be switched freely by selecting appropriate initial conditions.[44]With the further development of memristor research,fractional-order locally-active memristors are developed. For example,Xieet al.proposed a fractionalorder memristor with infinite locally-active interval and coupled it to Chen’s chaotic system. They found that the system presents different states under different fractional orders.[45]However, up to now, few studies have been carried out on fractional neuron models with locally-active memristors as autapses.
Inspired by the above studies, a fractional-order multistable locally-active memristor is proposed in this paper,and a neuron model is developed by regarding the proposed locallyactive memristor as the autapse of a fractional-order HR neuron. The main contributions of this work are summarized as follows. Firstly,a fractional-order locally-active memristor is developed. Its nonvolatile memory and locally-active characteristics,initial value-dependent coexisting pinched hysteresis loops and fractional-order-dependent electrical behavior are analyzed. Secondly, firing activities of the fractional-order memristive neuron model under different external conditions are studied. Finally,a neuron circuit with variable fractionalorder is proposed and the circuit simulation verification is performed.
The layout of this paper is as follows. In Section 2,a fractional-order tristable locally-active memristor is introduced and its related characteristics are studied in detail. In Section 3,a 4D fractional-order neuron model,by considering the fractional-order locally-active memristor as the autapse of 3D-HR neuron, is proposed, and the stability of the neuron model is analyzed. In Section 4, the influences of coupling strength, external excitation current and fractional-order on the firing activities of the fractional-order neuron model are discussed. In Section 5,the circuit simulation of the proposed fractional-order neuron model is carried out, and the conclusion is given in the last section.
2. Model and characteristics of fractional-order multistable memristor
It is well known that there are three definitions for fractional calculus, i.e., Gr¨unwald–Letnikov (GL) definition,Riemann–Liouville (RL) definition and Caputo definition.Among them,Caputo definition is very suitable for real world applications due to its initials with the same form as those of its integer order counterparts. In this paper, the Caputo definition, thus, is used to characterize the neuron model and the Caputo definition off(t)is described as

where 0<α <1 is the fractional-order,nis the first integer which is not less thanαand Γ(·)is the Euler gamma function.
2.1. Fractional-order multistable memristor model
In this paper, a fractional-order multistable locallyactive memristor is proposed, which is defined by the statedependent Ohm’s law

whereiandvrepresent the input current and input voltage,φis the internal state variable andG(φ)=nφis the defined memductance function. The corresponding state equation can be described as
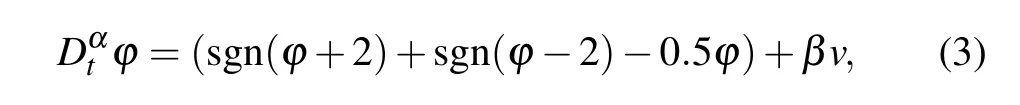
whereβis the memristive parameter.It is worth noting that the fractional-order state equation is constructed with sign functions,which are related to the internal stateφand the terminal voltagev. Compared with the existing locally-active memristors whose state equations are implemented with polynomial functions,[36,38,39]the proposed fractional-order locally-active memristor is more convenient for circuit implementation with low cost. In the following, we study the basic characteristics of the memristor from the aspects of pinched hysteresis loop,nonvolatile memory and locally-active characteristics.
2.2. Pinched hysteresis loop
A pinched hysteresis loop is one of the important characteristics of memristor. When the parameterβ=0.2 and the orderα=0.9,a sinusoidal voltagev=Asin(2πFt)with amplitudeA=2 is applied to the memristor,and the pinched hysteresis loops with different excited frequencies are shown in Fig. 1(a). It can be seen from Fig. 1(a) that when the input frequencyFincreases from 0.314 to 31.4,the lobe area of the pinch hysteresis loop gradually decreases and finally shrinks into a straight line atF=31.4,resulting in that the memristor degenerates into a fixed resistance.
In addition, whenA= 2 andF= 0.314 remain unchanged,three stable pinched hysteresis loops can be obtained under different initial statesφ0=-4, 0, and 4, as shown in Fig. 1(b). In order to study the influence of fractional-orderαon the pinched hysteresis loop, keepA=2,F=3.14, and memristor initial valueφ0=0, the fractional-orderαis selected as 0.98,0.9,0.8,0.7,and 0.5,respectively,and the hysteresis loops of the memristor are shown in Fig. 1(c). It is observed that the smaller the fractional-order is,the larger the lobe area of the hysteresis loop is,and thus the better memory of the memristor is.[46]

Fig.1. Pinched hysteresis loops. (a) Hysteresis loops with respect to different frequencies. (b) Initial value dependent pinched hysteresis loops, and (c)fractional-order dependent pinched hysteresis loops.
2.3. Nonvolatile memory and locally-active characteristics
Nonvolatility is also a key feature of the memristor,meaning that it can maintain its latest memductance value even after the applied power is removed. Usually,the power-off plot(POP) is used to judge whether an electronic device is nonvolatile. Let the input voltagev= 0, and the state Eq. (3)becomes
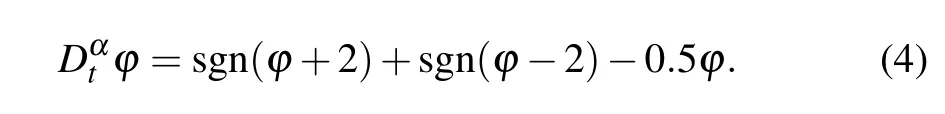
Whenα=0.9,the POP of the fractional memristor is shown in Fig.2(a). It can be seen from Fig.2(a)that the POP has five intersections with thex-axis,among which three intersectionsE1(-4,0),E3(0,0), andE5(4,0) are negative slope intersections and the other two intersectionsE2(-2,0) andE4(2,0)have an infinite positive slope. The arrows near the intersections in Fig. 2(a) indicate the moving direction of the POP.It is easy to know that the three negative slope intersections are stable equilibrium points and the others two positive slope intersections are unstable equilibrium points. The proposed memristor,thus,can exhibit three stable states,which are dependent on the initial valuesφ0,namely,

Whenn=1,the corresponding memductance values are
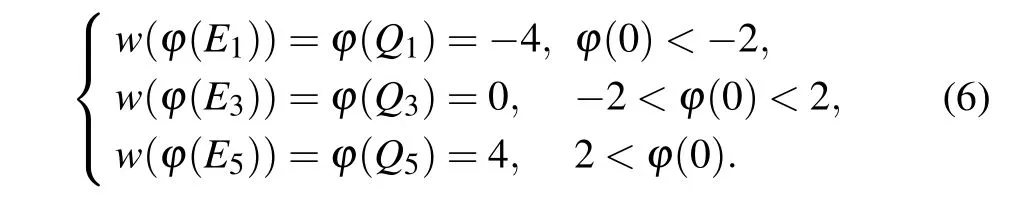
Thus, the proposed memristor is nonvolatile and it acts as a discrete memory device, which can encode three memory states.
DCV–Icurve is an important tool to judge whether the memristor has local activity. When the DCV–Icurve of the memristor has a negative slope, it is locally-active.[47]Letφ=0,Eqs.(2)and(3)can be written as
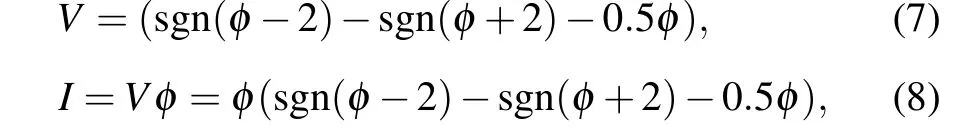
whereVandIdenote DC voltage and current, respectively,andΦis a variable equilibrium state which satisfiesDαt φ=(φ=Φ)=0. By virtue of Eqs.(6)and(7),the DCV–Icurve of the memristor is obtained and shown in Fig. 2(b). As can be seen from Fig. 2(b), there are three negative slope curves of red,green,and blue,which indicates that the memory resistor has three local active regions. That is,the fractional-order memristor is locally active and is suitable for realizing electronic synapse.
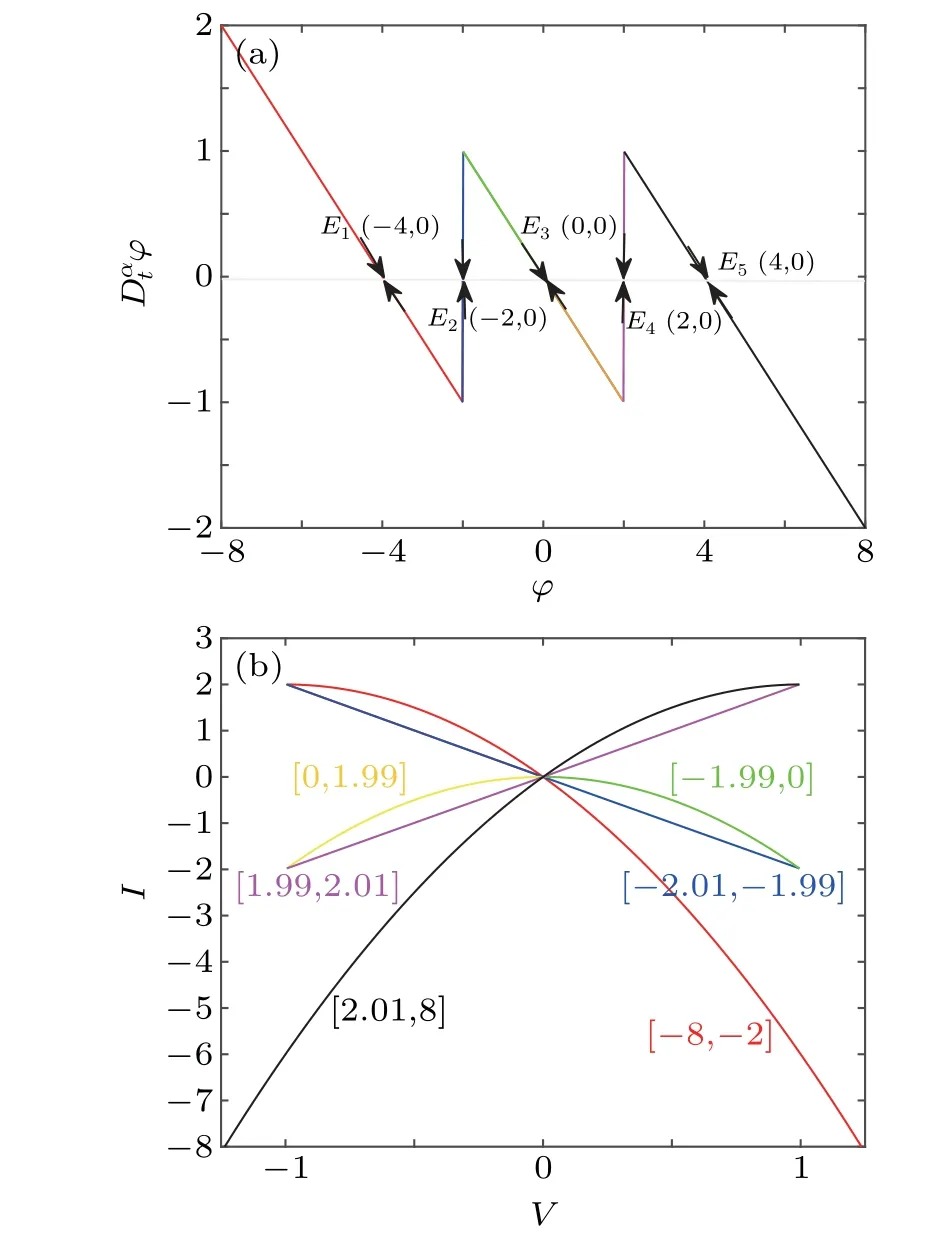
Fig.2. (a)The power-off-plot(POP)and(b)the DC V–I curve of the locally active memristor.
3. Fractional-order memristive neuron model and its stability analysis
3.1. Fractional-order memristive HR model
According to the Caputo definition, the fractional-order HR neuron model can be described as the following differential equations:
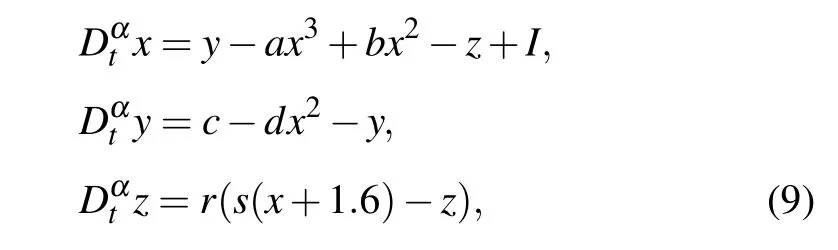
wherexrepresents the membrane potential,yis the recovery or spiking variable,zis the adaptation variable,Iis an external excitation current,αis the system order anda,b,c,d,r,sare system parameters. In this study, we consider the proposed locally-active memristor governed by Eqs. (2) and (3)as an autapse of the fractional-order HR neuron(9),then a 4D neuron model is developed,which is formulated as

wherekis the coupling strength. In this paper, the parameters are determined asa=1,b=3,c=1,d=5,r=0.0021,s=4,andβ=0.2. The effects of external excitation currentI,fractional-orderα,and coupling strengthkon the firing dynamics of the memristive neuron model are discussed in detail in Section 4.
3.2. Stability analysis of equilibrium points
In order to analyze the stability of the equilibrium point of the fractional-order neuron,the following theorem is introduced.
Lemma 1[48]For a fractional-order system with order 0<α ≤1:
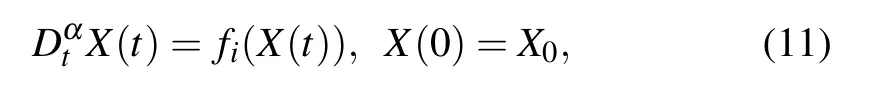
where

E(x0,y0,z0,φ0)is a fractional-order system equilibrium point.If all the eigenvaluesλi(i=1,2,3,...,n)of the Jacobian matrix satisfy the following condition:

the equilibrium point is asymptotically stable.
Let the right side of Eq. (10) equal to 0, the equilibrium point of the system can be written asE(x0, 1-,4(x0+1.6),φ0),wherex0andφ0are determined by

It can be seen from Eq.(13)that the equilibrium point of the system is related to the external excitation currentIand the coupling strengthk.The Jacobian matrix of system in Eq.(10)at equilibrium pointEis expressed as
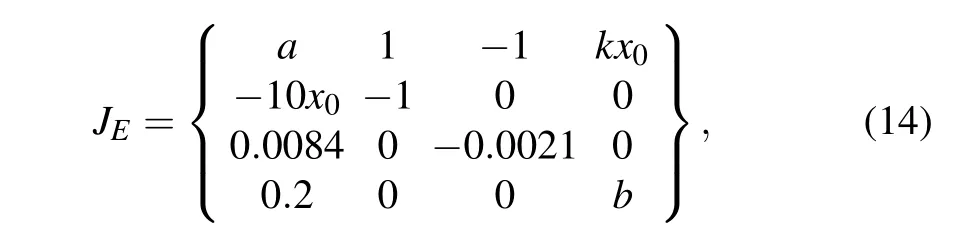
where

The characteristic equation of system in Eq. (10) at equilibrium pointEis
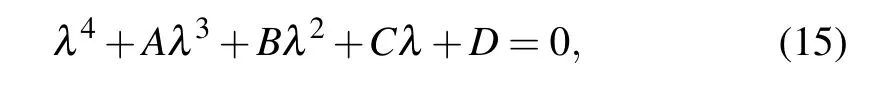
where


Withk=0.1,I=2.7,and other parameters remain unchanged,the two expressions in Eq.(13)can be graphically expressed,as displayed in Fig.3. As we can see from Fig.3,two curves govern by Eq. (13) have five intersections, whereφ0is equal to-2 at the pointE4and 2 at the pointE5. However, whenφ0=-2 or 2, Eq. (13) has no solution, therefore,E4andE5are not equilibrium points. The system, thus, has three equilibrium pointsE1,E2andE3.
In order to discuss the influence of external excitation currentIand the fractional-orderαon the stability of the equilibrium points, we list the eigenvalues of the three equilibrium points and the relationship between stability and their fractional-order under different external excitation currentI=1.27, 1.5, 1.95, and 2.7, as shown in Table 1. According to Eq.(15),each equilibrium point has four eigenvalues,and the stability of each equilibrium point is judged by Lemma 1.
According to Lemma 1 and Table 1, we can find when the real parts of the eigenvalues of the equilibrium points are all less than 0, the neuron is stable and independent of the fractional-orderα. When the eigenvalues of the equilibrium point have both positive real parts and imaginary parts, the stability of the equilibrium point is decided by the fractionalorderα. When the eigenvalues of the equilibrium point of the neuron have pure positive real roots,the system is unstable and independent of the fractional-orderα.

Fig.3. Two function curves and their intersections,wherein E1,E2, and E3 are equilibrium points,E4 and E5 are not equilibrium points.

Table 1. Equilibrium points and their stability when k=0.1.
4. Dynamic analysis
In order to study the dynamic behaviors of the neuron,nonlinear dynamical analysis tools such as time series, phase diagram,bifurcation diagram,Lyapunov exponent and ISI bifurcation diagram are used to analyze the firing activities. In the process of numerical analysis, the system parameters are fixed asa=1,b=3,c=1,d=5,r=0.0021,s=4, andβ= 0.2. It should be noted that the Adomian fractionalorder algorithm[49]is adopted in this paper,the step length of simulation ish=0.01, the computing software used is Matlab2019b, and the computer system is based on the Win10 home edition.
What needs special attention is that many studies have shown that autonomous and non-autonomous fractional-order systems do not have any exact periodic solution.[50,51]However,when the trajectory of a fractional-order system satisfies(t+T)-xi(t)=0,i=1,2,3,...,n,forT >0,according to Ref. [52], this phenomenon is named asymptoticallyT-periodic oscillations. Some studies have shown that there exist asymptotically periodic oscillations in the fraction-order circuits and systems.[45,52–54]In this paper,we also find the existence of asymptotically periodic oscillations in the proposed fractional-order neuronal model. To facilitate recording, the term “asymptotically periodic” is written as “A-periodic” in the following.
4.1. Coexisting firing behavior
In order to explore the coexisting firing behavior of the fractional-order neuron model,the system parameters are fixed ask= 0.1,α= 0.9,I= 2.7, andβ= 0.2, the initial values of the fractional-order neuron model are (1, 0, 0,-4),(1, 0, 0, 0), and (1, 0, 0, 4). The corresponding time series of the membrane potentialxare shown in the Figs.4(a)–4(c) respectively. From Figs. 4(a) and 4(b), we know thatxi(t+T)-xi(t)=0 andxi(t+T)-xi(t)=0 are established and the neuron has two A-periodic solutions. Although they are both A-periodic solutions,they exhibit different firing patterns. As illustrated in Fig. 4(a), the neuron exhibits irregular A-periodic bursting oscillations, in which the repetitive firing amplitude decreases gradually until it disappears in each burster.[55]While in Fig.4(b),the system shows A-periodic bursting oscillations,in which there exist seven firing pulses with approximately equal amplitude in each burster.However,when the initial value of the fractional neuron model is(1, 0, 0, 4), no periodTsatisfiesxi(t+T)-xi(t)=0,and thus,the neuron shows a chaos oscillation state,as shown in Fig.4(c). From Fig.4(d),we find the neuron model can exhibit three distinct firing patterns under different initial values.

Fig.4. Firing patterns of the fractional-order neuron. (a)–(c) Time series of the membrane potential x with the initial values (1, 0, 0, -4), (1, 0, 0,0),and(1,0,0,4),respectively. (d)Phase diagrams,where black,red,and green respectively represent the initial value of (1, 0, 0, -4), (1, 0, 0, 0),and(1,0,0,4)).
In order to verify the above three different firing patterns, the initial valueφ0of the memristor is considered as the controlled parameter and the others parameters remain unchanged. The bifurcation diagram and Lyapunov exponents with respect to the initial valueφ0are obtained in Figs. 5(a)and 5(b), respectively. For clarity, the others two Lyapunov exponents LE3 and LE4 in Fig.5(b)are neglected since their values are much less than 0. When the initial valueφ0locates at the region of(-6,-2)and(-2,2),the system is A-periodic.While when the initial valueφ0is in the region of (2, 6), the system presents a chaotic state. From Fig. 5(b), we can find that the maximum Lyapunov exponent is approximately equal to 0 when the initial valueφ0locates at (-6, 2) and (-2, 2),meaning the neuron is in an A-periodic oscillation state;while the maximum Lyapunov exponent is greater than 0 when the range of initial valueφ0is(2,6),showing that the neuron produces chaotic oscillation behavior.So,the bifurcation diagram and the Lyapunov exponents are well consistent.

Fig.5. (a) Bifurcation diagram of x with memristor initial value φ0. (b)Lyapunov exponents with memristor initial value φ0.
4.2. Influence of excitation current
In the real world,neurons respond differently to different external stimuli. In this part,we discuss the effect of the excitation currentIon the fractional neuron model. Keepα=0.9,k=0.1,β=0.2 and the initial value of the system as(1,0,0,4),when the external excitation currentIchanges from 1.4 to 3.1,the ISI bifurcation diagram and Lyapunov exponents[56,57]are shown in Figs. 6(a) and 6(b), respectively. Similarly, the others two Lyapunov exponents LE3 and LE4 are neglected because their values are much less than 0.

Fig.6. (a)ISI bifurcation diagram and(b)Lyapunov exponents with respect to the external excitation current I.
In a fractional-order system,if the trajectory of the system is A-periodic oscillation in some intervals,while the trajectory of other adjacent regions is chaotic,this phenomenon is called“local chaos”.[42]From Fig. 6(a), as the external excitation currentIincreases from 1.5 to 2.6,the firing frequency of the fractional-order neuron gradually increases from A-periodic-1 to A-periodic-4. WhenIincreases from 2.6 to 3.1, the neuron appears an A-periodic–chaos–A-periodic switching process. Namely,the neuron presents local chaos. The Lyapunov exponents shown in Fig. 6(b) also verify the effect of the external excitation currentIon firing activity of neuron model.
4.3. Influence of coupling strength
Set the fractional-orderα=0.9,β=0.2,I=2.7,and the initial value of the system is(1,0,0,0). The coupling strengthkis considered as the controlled parameter to explore its influence on the firing dynamics of the neuron model. When the coupling strengthkincreases from 0.1 to 1.4,the ISI bifurcation diagram and the corresponding Lyapunov exponents are illustrated in Figs.7(a)and 7(b),respectively. From Figs.7(a)and 7(b), when coupling strengthk ∈(0,0.5), the system is in an A-periodic state;when coupling strengthk ∈(0.5,0.95),the system alternates between A-periodic and chaotic states.As the coupling strengthkincreases from 0.95 to 1.4,the neuron undergoes a series of inverse period doubling bifurcations and finally shows A-period 1 oscillations.

Fig.7. The effect of the coupling strength on firing patterns. (a)ISI bifurcation diagram and(b)Lyapunov exponents. The initial value is(1,0,0,0)and I=2.7,α =0.9.
4.4. Influence of fractional-order
The firing frequency of neuron has great influence on the transmission and processing of neural signals. The more spikes in per unit of time,the action and the firing frequency of neuron will become faster. In order to study the effect of the fractional-orderαon the firing frequency of the fractionalorder neuron model, setk=0.1,β=0.2,I=2.7, and the fractional-orderαvaries from 0.55 to 1. The ISI bifurcation diagram of the fractional neuron with the initial value of(1,0,0,4)is shown in Fig.8.
From Fig. 8, whenαincreases from 0.55 to 0.7, the neuron exhibits A-periodic firing and the ISI of the neuron increases gradually, meaning the firing frequency decreases gradually. Figures 9(a) and 9(b) illustrate the time series of the membrane potentialxwith the fractional-orderα=0.6 and 0.68, respectively. In the duration oft=(1000,1200),Fig. 9(a) contains 6 complete A-periodic oscillations, while there are just 4 complete A-periodic oscillations in Fig. 9(b).So, we can intuitively observe that the firing frequency decreases as the increase of the fractional-orderα.
However,from Fig.8,as the fractional-orderαincreases from 0.7 to 1, the firing pattern of the neuron changes from A-periodic to chaotic firing. In order to verify the transition of firing pattern, the time series of the membrane potentialxwithα=0.7 and 0.8 are provided in Figs.10(a)and 10(b),respectively. And the corresponding phase diagrams are shown in Figs.10(c)and 10(d). It is easy to find when the fractionalorder is 0.7,the neuron exhibits A-periodic 5 oscillation,while forα=0.8,the neuron is in chaotic oscillation state.

Fig.8. Inter spike interval(ISI)bifurcation diagram with fractional-order α.
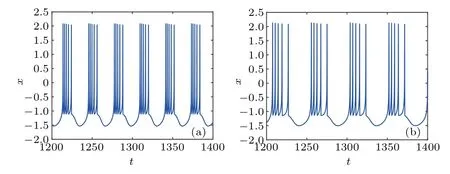
Fig.9. The membrane potential with different orders. (a) α =0.6, (b)α =0.68.
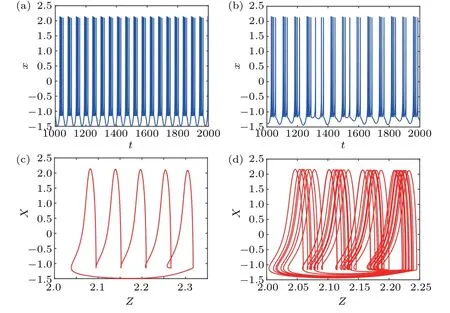
Fig.10. Firing patterns with respect to the fractional-order α. The initial value of the neuron is(1,0,0,4),I=2.7 and k=0.1. (a)and(b)The time series of the membrane potential with α =0.7 and α =0.8,respectively,(c)and(d)The corresponding phase diagrams.
5. Circuit simulations
5.1. Schematics and circuit parameter selections
In this section, the memristive autapse coupling neuron model governed by Eq. (10) is realized by using the off-theshelf electronic components, as shown in Fig. 11, in which the operational amplifiers TL082CD and the analog multipliers AD633AN are biased with±15 V voltage. From Fig.11,the complete system circuit consists of three modules: memristor module,αorder module and neuron module. It should be noted that theMabove the operational amplifier represents the fractional-order capacitor. According to the Kirchhoff’s current law, the circuit shown in Fig. 11 can be described by the following equations:

where four state variablesVx,Vy,Vz, andVφ, denote capacitor voltages of four integral circuit channels,respectively,andτ1=τ2=τ3=τ4=R0C0are time constants of each channel. Comparing the dynamical Eq.(16)with the neuron model Eq. (10), when the circuit parameters and system parameters satisfy the following relations:


then the circuit Eqs. (16) are equivalent to those of Eq. (10).The proposed circuit can simulate the firing dynamics of the fractional-order neuron. Fixing the system parameters asa=1,b=3,c=1,d=5,r=0.0021,s=4,β=0.2,k=0.1 and lettingτ1=τ2=τ3=τ4=100, we can obtain the following specific values of the circuit parameters:g1=g3=g4=1,R0=10 kΩ,C0=1 μF,Ra=R1=R7=R8=R9=R11=R12=R13=R15=R16=10 kΩ,Rb=100 kΩ,R6=50 kΩ,Rf= 1 kΩ,R3=R4= 13.5 kΩ,R5= 2 kΩ,R10= 1 kΩ,R14=2 kΩ,R17=1190.47 kΩ,R18=744.047 kΩ,R19=4761.9 kΩ,R20=10 kΩ,V1=V2=V3=1 V.
According to Ref. [58], the equivalent expression ofαorder capacitor in complex frequency domain can be written as

wherenis the number of unit integrating units. When fractional-order capacitors withα=0.7, 0.8, 0.9, and 0.98,according to Refs. [59,60], we can obtain the following expressions:

The corresponding resistance and capacitance values with different fractional-orderαare listed in Table 2. In the fractionalorder capacitor module,the switching elements are used to realize different fractional-orders. For example,when the switchK1is closed and the others switches are turned off,Mis a fractional-order capacitor withα=0.98. In this way,we can obtain other three fractional-order capacitors.

Table 2. The resistance and capacitance values of the α-order capacitors.
5.2. Circuit simulation results
Referring to the circuit schematic diagram provided in Fig. 11, the fractional-order memristive HR neuron circuit is designed based on the Multisim 14.0. According to the voltage dividing principle of shunt capacitor,the initial voltage of shunt capacitor is equal to the sum of all shunt capacitors. For the convenience of design,only the initial value of the capacitorC1is changed and the initial values of the others capacitors are set to 0 in the fractional-order capacitor module.
Firstly, we simulate the electrical behavior of the fractional-order memristor by using Multisim 14.0. ClosingK2so that the fractional-orderα=0.9,applying a sinusoidal voltage with amplitudeA=2 V and frequencyF=3.14 Hz to the fractional-order memristor,we obtain three stable pinched hysteresis loops with different initial values. As illustrated in Fig. 12(a), the red, green, and blue hysteresis loops are related toVC1=4 V, 0 V, and-4 V, respectively. Thus, the circuit simulation results effectively verify the numerical simulation results shown in Fig.1(b),indicating that the proposed fractional-order memristor can indeed exhibit the coexisting hysteresis loops. LetVC1=0 V, and closeK4,K3,K2, andK1sequentially, the corresponding pinched hysteresis loops corresponding to different fractional-orders are provided in Fig. 12(b), which are similar as the numerical simulation results illustrated in Fig.1(c).
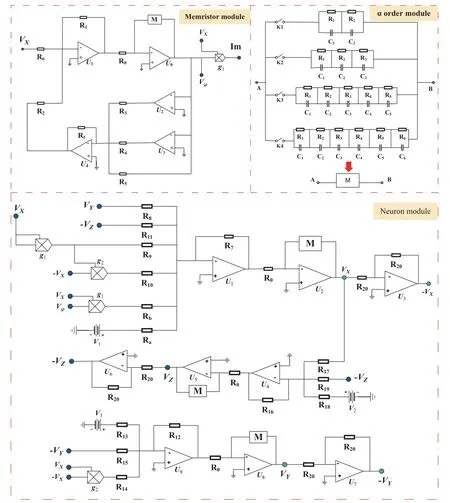
Fig.11. The main circuit of fractional-order neuron model including memristor module,α order module and neuron module.
Secondly, the coexisting firing patterns of the memristive neuron are also verified by Multisim circuit simulation.CloseK2so that the fractional-orderα=0.9,letVC1=-4 V,0 V,and 4 V,respectively,the corresponding time series of the membrane potentialxwith different initial values are shown in Figs.13(a)–13(c)and the corresponding phase portraits inz–xplane are illustrated in Fig. 13(d). From Fig.13, we can find that the neuron circuit exhibits three coexisting firing patterns,namely, irregular A-periodic oscillations, A-periodic-7 oscillations and chaotic oscillations,which are well consistent with the numerical simulation results illustrated in Fig.4.
Finally, the firing activities of the neuron circuit dependent on different fractional-orders are plotted in Fig. 14. For simplicity, we only consider two cases, namely,α=0.7 andα=0.8.When only the switchK4is closed,the corresponding fractional-order isα=0.7,we find the neuron circuit exhibits A-periodic bursting with 5 spikes,the corresponding time series and phase diagram are plotted in Figs. 14(b) and 14(a).WhileK3is on, which meansα=0.8, we can observe complex chaotic firing activities, as illustrated in Figs. 14(d) and 14(c). From the numerical simulation results in Fig. 10 and the circuit simulation results in Fig. 14, it is easy to find that the fractional-order has an important effect on the firing activities of the memristive neuron.

Fig.12. The pinched hysteresis loops obtained by circuit simulation. (a)Three stable hysteresis loops with different initial values,(b)hysteresis loops with different fractional-orders.

Fig.13. The coexisting firing patterns in circuit simulation. (a)–(c)The time series of the membrane potential with VC1=-4 V,0 V,and 4 V,respectively,and(d)phase diagram in Vz–Vx plane.
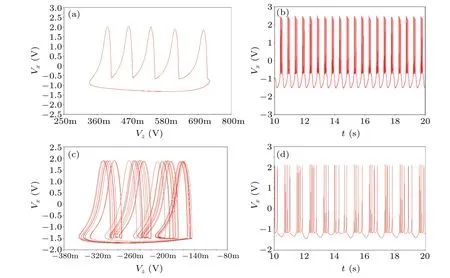
Fig.14. The fractional-order dependent firing activities. (a)The time series and(b)phase diagram with α =0.7,(c)the time series and(d)phase diagram with α =0.8.
6. Conclusion
In this paper, a multistable fractional-order locallyactive memristor is proposed, and its nonvolatile and locallyactive characteristics are studied and analyzed. Then, a 4D fractional-order HR neuron model is developed by introducing the designed memristor as an autapse of a fractional-order 3D HR neuron model. The effects of initial value, coupling strength, external excitation current and fractional-orderαon the firing activities of the fractional-order neuron model are discussed in detail by numerical and circuit simulations.Some complex firing phenomena including the coexisting firing patterns ignited by different initial values, alternation of A-periodic and chaotic firing induced by coupling strength,are observed. Furthermore, we find that the fractional-orderαcan not only affect the firing patterns but also change the firing frequency of the neuron. It is expected that this study will be helpful to the theoretical analysis and understanding of the fractional-order locally-active memristor and the firing activities of the fractional-order neuron.
Acknowledgments
Project supported by the National Key Research and Development Program of China (Grant No. 2018AAA0103300)and the National Natural Science Foundation of China(Grant Nos.62171401 and 62071411).
杂志排行
Chinese Physics B的其它文章
- The coupled deep neural networks for coupling of the Stokes and Darcy–Forchheimer problems
- Anomalous diffusion in branched elliptical structure
- Inhibitory effect induced by fractional Gaussian noise in neuronal system
- Enhancement of electron–positron pairs in combined potential wells with linear chirp frequency
- Enhancement of charging performance of quantum battery via quantum coherence of bath
- Improving the teleportation of quantum Fisher information under non-Markovian environment
