分组密码最小活跃S 盒个数快速搜索算法

刘正斌，李永强，朱朝熹

（1.保密通信重点实验室，四川 成都 610041；2.中国科学院信息工程研究所，北京 100093）

0 引言

差分密码分析[1]和线性密码分析[2]是密码分析中最有效的2 种分析方法，抵抗差分密码分析和线性密码分析是现代分组密码最基本的一项设计准则。评估分组密码抵抗差分密码分析和线性密码分析的主要方法包括计算最大差分/线性特征的概率和计算最小活跃S 盒个数。对于代入置换网络（SPN,substitution permutation network）型分组密码，根据宽轨迹设计策略[3]，可以得到抵抗差分密码分析和线性密码分析的可证明安全界。通过计算最小活跃S 盒个数，并结合S 盒的最大差分概率和线性概率，设计者可以计算出最大差分特征概率和线性特征概率的上界。目前，学术界已经提出了一些自动化搜索算法来辅助评估分组密码的安全性。

1994 年，Matsui[4]提出一种分支定界搜索算法来自动化搜索分组密码DES（data encryption standard）的最优差分特征和线性特征，该算法也称Matsui 算法。尽管该算法能够在有限时间内找到DES 的16 轮最优差分特征和线性特征，但是对于其他一些分组密码，它的效率却非常低。随后，Ohta 等[5]和Aoki 等[6]分别改进了Matsui 算法，找到了分组密码 FEAL（fast data encipherment algorithm）的最优差分特征和线性特征。虽然Matsui 算法可以扩展到搜索SPN 型分组密码的最优差分特征和线性特征，但是其线性层的快速扩散性质和雪崩效应严重降低了搜索效率。对于使用比特置换层的SPN 型分组密码，Arnaud 等[7]优化了Matsui 算法并找到了分组密码PRESENT、PUFFIN 和ICEBERG 的全轮最优差分特征。Ji 等[8]则通过引入3 种加速方法来提高Matsui 算法的搜索效率，并找到了DESL 和GIFT 约减轮数的最优差分特征和线性特征。Kim 等[9]改进了Matsui 算法来搜索SPN 型分组密码的最优差分特征和线性特征。

2011 年，Mouha 等[10]提出了一种基于混合整数线性规划（MILP,mixed integer linear programming）的方法来搜索SPN 型分组密码的最小活跃S 盒个数。Sun 等[11]将基于MILP 的方法扩展到使用比特置换层的分组密码，提出了2 种能够精确刻画S 盒的差分和掩码传播的方法，即逻辑条件模型和凸包计算，并给出了约减不等式组的贪婪算法。Abdelkhalek 等[12]将逻辑条件模型中约束条件的生成问题转化成布尔函数的和积的最小化问题，并使用Quine-McCluskey 算法[13-14]和Espresso 算法[15]来建立8 bit S 盒的差分分布表的比特模型。为了提高基于MILP 方法的效率，Zhang 等[16]在MILP 模型中引入了分支定界策略来减少约束条件，降低搜索空间；Zhou 等[17]则使用分而治之的方法来优化模型求解。近几年，基于MILP 的方法被广泛应用于分组密码的设计与分析中[18-30]。

除了算法模型的优化外，基于MILP 方法的效率主要由求解器的效率决定，如CPLEX、Gurobi等。对于轮数较长或者轮函数较复杂的分组密码，由于需要更多的变量和不等式来描述差分和掩码的传播，因此求解器通常需要执行非常长的时间来得到最优解。对于攻击一个已知的分组密码，花费十几天甚至几个月的时间是有意义的。然而，从分组密码设计的角度，为了优化密码部件（S 盒、扩散矩阵等）的选择以及确定合理的迭代轮数，设计者通常需要进行多次安全性评估。因此，一个快速搜索最小活跃S 盒个数的算法对于评估分组密码抵抗差分密码分析和线性密码分析的安全性具有重要意义，在分组密码设计过程中具有重要实用价值。

本文主要的研究工作如下。

1) 提出了扩散矩阵的差分/掩码模式分布表的概念。对于二元域矩阵，证明了通过遍历输入差分/掩码方式来构造差分/掩码模式分布表的计算复杂度的下界。基于该下界，给出了构造差分/掩码模式分布表的快速方法。

2) 对于任意阶最大距离可分（MDS,maximum distance separable）矩阵，证明了满足分支数条件的差分/掩码模式一定能够实例化，即对于特定的差分/掩码模式，一定存在对应的差分/掩码传播。基于分支数关系，给出了任意阶MDS 矩阵的差分/掩码模式的传播集合。

3) 基于差分/掩码模式分布表，提出了一种自动化搜索分组密码最小活跃S 盒个数的快速算法。针对SPN 型分组密码，通过实验验证了该算法的有效性。实验结果表明，本文算法效率比目前常用的基于MILP 的方法高。

1 差分/掩码模式分布表

1.1 差分/掩码模式分布表定义

对于双射S 盒，设ΔX和ΔY分别表示S 盒的输入差分模式和输出差分模式，则ΔY=0当且仅当ΔX=0，ΔY=1当且仅当ΔX=1，反之亦然。

对于线性变换y=Ax，A是一个n阶矩阵，设输入差分 为 Δx=(Δx1,…,Δxn)，则输出差分为Δy=AΔx。令 ΔX=(ΔX1,…,ΔXn)表示输入差分模式，ΔY=(ΔY1,…,ΔYn)表示输出差分模式，那么(ΔX,ΔY)就称为线性变换的一个差分模式传播。

定义4差分模式分布表。线性变换的差分模式分布表（DPDT,difference pattern distribution table）是一个表示其输入差分模式和输出差分模式的分布表。对于给定的输入差分模式ΔX=(ΔX1,…,ΔXn) ∈和输出差分模式ΔY=(ΔY1,…,ΔYn) ∈，令α= ΔX1‖…‖ ΔX n，β= ΔY1‖…‖ ΔY n，那么差分模式分布表中第α行、第β列元素DPDT(α,β)=1表示一定存在与(ΔX,ΔY)对应的差分传播(Δx,Δy)，满 足Pr(Δx→ Δy) ≠0，其中，Pr(·)表示概率。

与差分模式分布表对应，可以定义线性变换y=Ax的掩码模式分布表。记输入掩码为Γx=(Γx1,…,Γxn)，那么输出掩码为 Γy=(AT)-1Γx。令ΓX=(ΓX1,…,ΓXn)表示输入掩码模式，ΓY=(ΓY1,…,ΓYn)表示输出掩码模式，那么(ΓX,ΓY)就称为线性变换的一个掩码模式传播。

定义5掩码模式分布表。线性变换的掩码模式分布表（MPDT,mask pattern distribution table）是表示其输入掩码模式和输出掩码模式的分布表。对于给定的输入掩码模式 ΓX=(ΓX1,…,ΓXn) ∈和输出差分模式ΓY=(ΓY1,…,ΓYn) ∈，令μ= ΓX1‖…‖ ΓX n，ν= ΓY1‖…‖ ΓY n，那么掩码模式分布表中第μ行、第ν列元素MPDT(μ,ν)=1表示一定存在与(ΓX,ΓY)对应的掩码(Γx,Γy)，满足

接下来，针对分组密码中最常用的2 种扩散矩阵——MDS 矩阵和二元域矩阵，给出其差分模式分布表和掩码模式分布表的构造。

1.2 MDS 矩阵差分/掩码模式分布表构造

首先证明MDS 矩阵的差分/掩码模式传播与其分支数之间的等价关系，然后基于分支数来构造MDS矩阵的差分/掩码模式分布表。

设m为正整数，为包含2m个元素的有限域。GLn()表示元素取自有限域上的n阶可逆矩阵的集合。对于Fq上的MDS 码，其码字分布有如下结果。

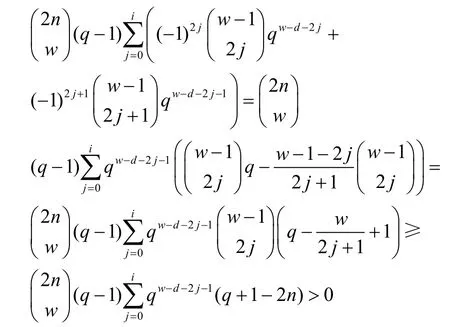
如果存在i，使w-d=2i，此时根据上述证明情况可得

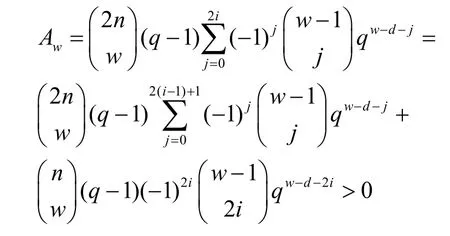
综上，定理2 证毕。

根据定理2，MDS 矩阵的差分/掩码模式分布表可以直接根据其分支数来构造。该方法只需要遍历差分/掩码模式，极大降低了差分/掩码模式分布表的计算复杂度，对于上n阶MDS 矩阵，计算复杂度从 O(2mn)降为 O(2n)。

1.3 二元域矩阵差分/掩码模式分布表构造

对于二元域矩阵，首先证明通过遍历输入差分/掩码来构造差分/掩码模式分布表的计算复杂度的下界，然后给出差分/掩码模式分布表的构造方法。

根据定理3，对于分组密码中常用的任意4 阶和8 阶二元域矩阵，构造其差分/掩码模式分布表的计算复杂度分别为 O(212)和O (232)，因此可以在计算机上非常快速地构造。然而，构造16 阶二元域矩阵的差分/掩码模式分布表需要 O (280)的计算量，因此无法通过这种方式直接构造。二元域矩阵差分模式分布表的构造如算法1 所示。在算法1 中，对于4 阶和8 阶二元域矩阵，d的值分别为3 和4。

算法1二元域矩阵差分模式分布表构造算法

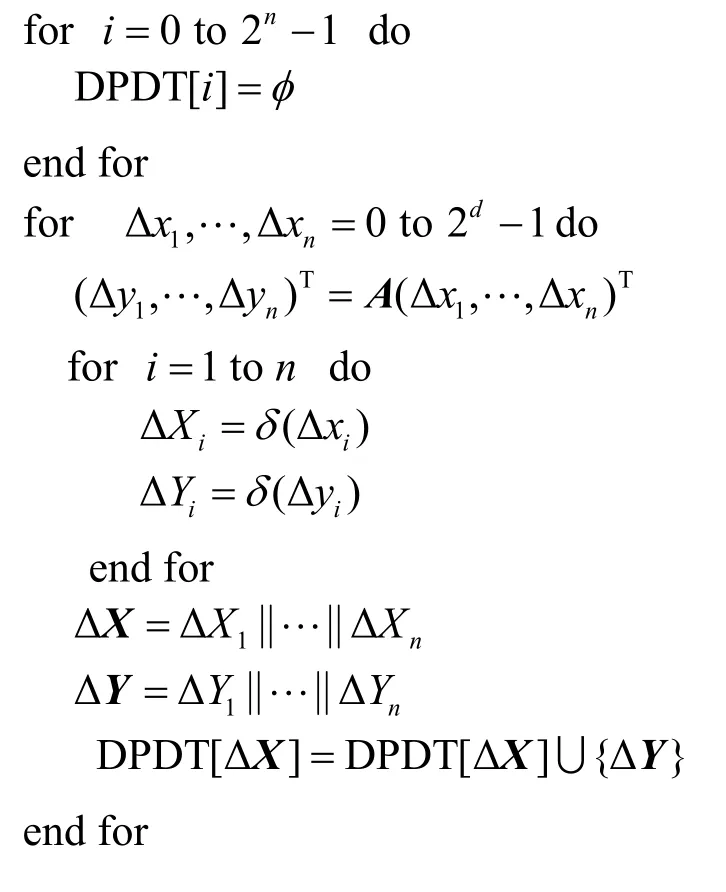
对于差分模式分布表的每一行，按照汉明重量从小到大的顺序对输出差分模式进行排序。掩码模式分布表的构造是类似的，只需要将其中的矩阵A替换为矩阵 (AT)-1。

2 SPN 型分组密码活跃S 盒个数搜索算法

2.1 分支定界搜索算法

Matsui 算法对差分特征和线性特征执行递归搜索，它根据已知的i轮最优特征概率Bi（1 ≤i≤r-1）和r轮最优特征概率Br的初始估计值来计算Br。对于任意，只要≤Br，Matsui算法一定可以得到r轮最优特征概率Br。对于Feistel密码，其轮函数的差分传播过程如图1 所示，其中，F表示轮函数中的一个变换。Matsui 算法搜索最优差分特征的伪代码如算法2 所示。

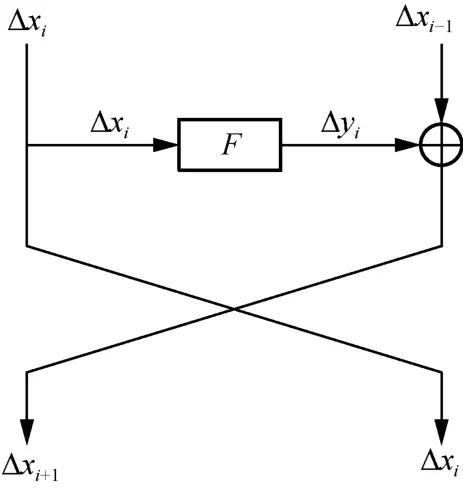
图1 Feistel 密码轮函数的差分传播过程

算法2Matsui 算法搜索最优差分特征

2.2 SPN 型分组密码最小活跃S 盒个数搜索算法

SPN 结构是现代分组密码最常用的一种密码结构，其轮函数包含一个非线性替换层和一个线性扩散层。非线性替换层又称S 盒层，它使用一组并行的S 盒；线性扩散层是一个线性函数，通常包含一个基于字的置换和一个基于矩阵乘法的线性变换。SPN 型分组密码最著名的实例是高级加密标准（AES,advanced encryption standard），它的轮函数包含字节置换（SubBytes）、行移位（ShiftRows）、列混淆（MixColumns）、轮密钥加（AddRoundKey）。

在轻量级密码领域，研究者提出了若干SPN 型轻量级分组密码。为了适用于资源受限环境，S 盒层通常使用4 bit S 盒，列混淆层则使用轻量级MDS矩阵或者二元域矩阵。不失一般性，本文仍然沿用AES 的轮函数结构，使用符号SB 表示S 盒层，SR表示线性置换层，MC 表示列混淆层，AK 表示轮密钥加。SPN 型分组密码的轮函数如图2 所示，其中，S 表示S 盒变换。

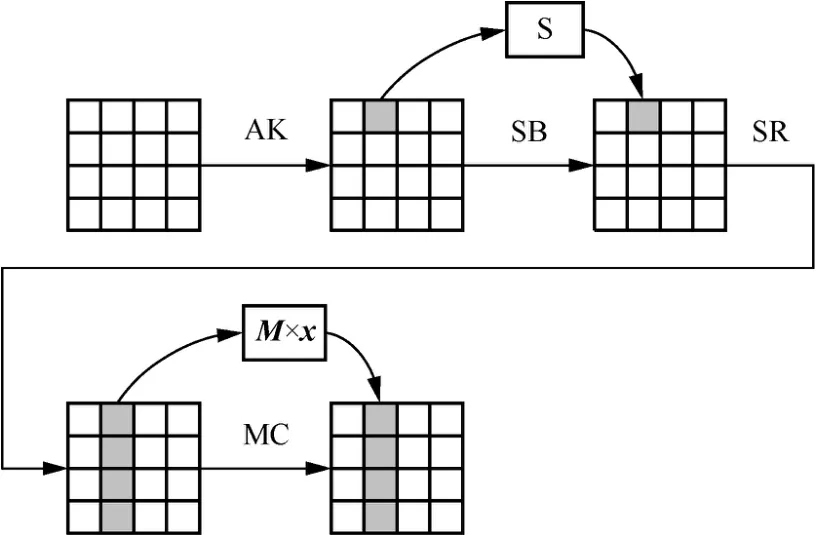
图2 SPN 型分组密码的轮函数

为了进一步提高搜索效率，算法3 引入了一些优化策略。

首先，按照汉明重量从小到大的顺序遍历明文差分模式，一旦某个汉明重量的差分模式不满足搜索条件，即n1+Br-1＞Br，就停止搜索，不需要遍历更高汉明重量的明文差分模式。这种策略使搜索空间非常小——只包含低汉明重量的差分模式，极大地提高了算法效率。

另外，由于差分模式分布表的输出差分模式按照汉明重量从小到大的顺序排列，对于给定的输入差分模式，每次查表都得到当前汉明重量最小的输出差分模式，即下一轮的活跃S 盒个数，可以更有效地排除不满足条件的差分模式。一旦某个输出差分模式不满足搜索条件，就可以提前停止，不需要继续搜索下一轮。

3 本文算法应用

将本文算法应用于SPN 型分组密码LED（Light encryption device）[32]、SKINNY[27]、CRAFT[28]以及认证加密算法FIDES[29]，找到了其全轮最小活跃S 盒个数的下界。对于随机选择的S 盒，该下界是紧致的，即对于一个特定的S 盒，可以构造一条有效的差分/线性特征。实验结果如表1～表4 所示，其中，#SD和#SL分别表示差分活跃S 盒个数和线性活跃S 盒个数，TOurA和TMILP分别表示本文算法和基于MILP方法的运行时间，—表示未给出或者未找到相应轮数的结果。与基于MILP 的方法相比，本文算法效率更高。

表1 LED 最小活跃S 盒个数

本文中所有实验都是在计算机上运行的，所用的实验平台是Intel Core i7-6700 CPU @3.4 GHz，16 GB RAM，软件采用VS2010，C 语言编程。

3.1 LED 分组密码

LED 是Guo 等[32]在CHES 2011 会议上提出的一组64 bit 分组密码，它包含2 个版本，即LED-64和LED-128，对应的密钥长度分别为64 bit 和128 bit。由于LED 的列混淆层使用MDS 矩阵，根据宽轨迹策略，可以证明LED 任意连续4 轮的最小活跃S盒个数为25 个。

本文通过自动化搜索程序找到了LED-64 和LED-128 全轮的最小活跃S 盒个数。对于LED-64，找到差分和线性活跃S 盒一共需要134 s。对于LED-128，找到差分和线性活跃S 盒一共需要201 s。实验结果如表1 所示，由于差分活跃S 盒与线性活跃S 盒个数相同，表1 仅列出了最小差分活跃S盒个数。表1 中r轮的时间是指在已知r-1 轮最小活跃S 盒个数的条件下，搜索r轮最小活跃S盒个数的时间，因此总的搜索时间是累积前r轮的时间。

3.2 SKINNY 分组密码

在CRYPTO 2016 会议上，Beierle 等[27]提出了一簇可调轻量级分组密码SKINNY，它包含2 种分组长度：64 bit 和128 bit，分别记为SKINNY-64和SKINNY-128。为了评估SKINNY 抵抗差分密码分析和线性密码分析的安全性，设计者使用基于MILP 的方法来搜索最小活跃S 盒个数，并找到了22 轮最小差分活跃S 盒个数，以及23 轮最小线性活跃S 盒个数。对于更多轮数，由于MILP求解器的运行时间太长，他们只提供了最小活跃S盒个数的上界。

本文找到了SKINNY 全轮的最小活跃S 盒个数，其中，搜索40 轮最小差分活跃S 盒个数需要10 s，最小线性活跃S 盒个数需要5 s，与基于MILP的方法相比效率非常高。实验结果如表2 所示。由于SKINNY-64 和SKINNY-128 使用相同的二元域矩阵（分别作用在和上），根据定理3，SKINNY-64 和SKINNY-128 的差分/掩码模式分布表相同，因此它们具有相同的活跃S 盒个数。

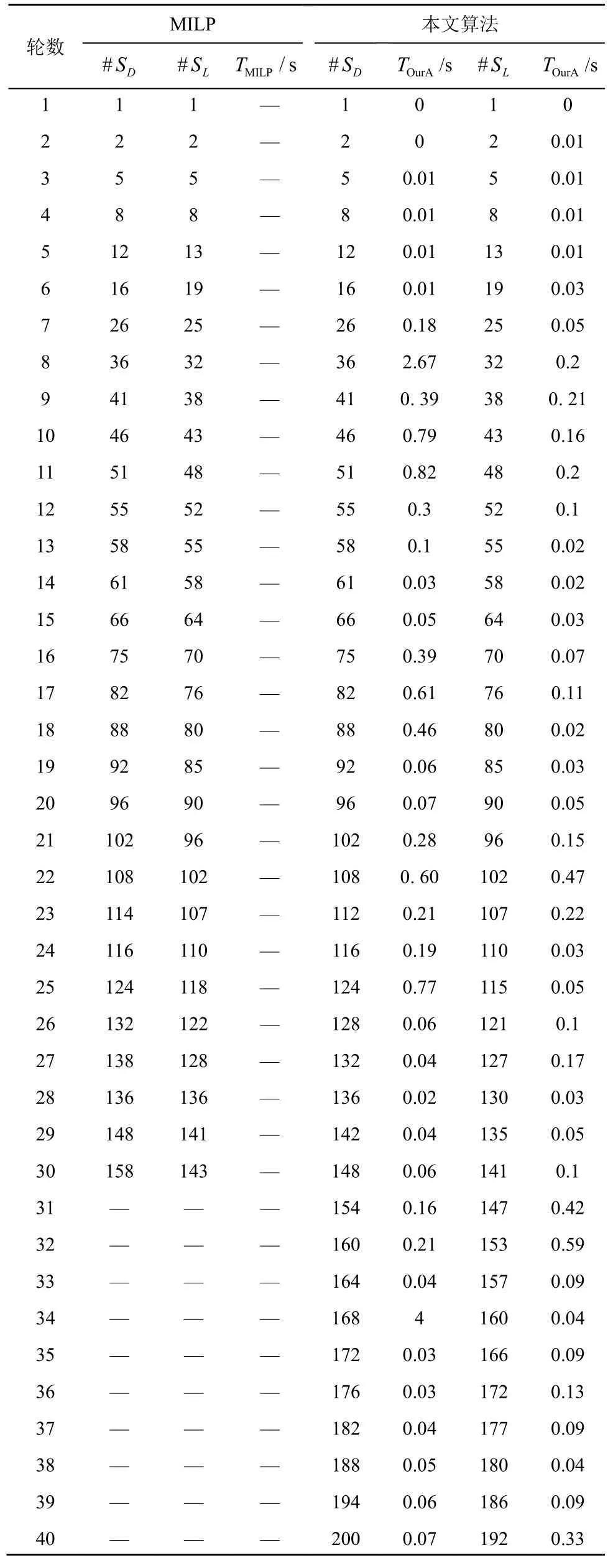
表2 SKINNY 最小活跃S 盒个数

3.3 CRAFT 分组密码

CRAFT 是Beierle 等[28]提出的一个可调轻量级分组密码，其分组长度为64 bit，密钥长度为128 bit，迭代轮数为31 轮。它的设计目标是实现对差分故障攻击的有效防护，以及以很少的额外代价同时实现加密和解密。为此，CRAFT 使用了对合的密码部件，并且没有使用密钥扩展算法。在算法分析方面，设计者同时使用Matsui 算法和基于MILP 的方法来评估其抵抗差分密码分析和线性密码分析的安全性，得到了17 轮最小差分活跃S 盒个数的下界。

本文找到了CRAFT 全轮的最小活跃S 盒个数，算法运行时间约为2 s，实验结果如表3 所示。由于CRAFT 使用对合的二元域矩阵，差分模式分布表和掩码模式分布表相同，因此差分活跃S 盒个数与线性活跃S 盒个数相同，表3 只列出了最小差分活跃S 盒个数。另外，与算法设计者直接使用Matsui算法相比，本文的优化策略对于Matsui 算法的效率提升非常明显。

表3 CRAFT 最小活跃S 盒个数

3.4 FIDES 认证加密算法

FIDES 是面向硬件的轻量级认证加密算法[29]，采用类似Duplex Sponge 结构和专门设计的内部置换。FIDES 包含2 个版本：FIDES-80 和FIDES-96，其内部状态分别为160 bit 和192 bit。FIDES 的加密算法采用SPN 结构，S 盒分别使用5 bit 的AB（almost bent）函数和6 bit 的APN（almost perfect nonlinear）函数，其初始化和生成标签的过程分别执行16 次轮函数迭代。

根据宽轨迹设计策略，FIDES 的任意连续4 轮至少有16 个活跃S 盒。为了得到更好的安全界，设计者使用基于MILP 的方法搜索最小活跃S 盒个数，并找到了8 轮最小活跃S 盒个数。然而，该MILP 模型并没有精确刻画列混淆矩阵的差分/掩码模式传播，因此无法保证5～8 轮最小活跃S 盒个数的下界是紧致的。

本文找到了FIDES 全轮的最小活跃S 盒个数，由于本文通过遍历列混淆矩阵的输入差分/掩码来计算其所有可能的差分/掩码模式传播，因此得到了最小活跃S 盒个数的紧致下界，实验结果如表4 所示。由于列混淆层使用对合二元域矩阵，其差分模式分布表和掩码模式分布表相同，因此差分活跃S盒个数与线性活跃S 盒个数相同，表4 只列出了最小差分活跃S 盒个数。另外，根据定理3，FIDES-80和FIDES-96 的差分/掩码模式分布表相同，因此具有相同的活跃S 盒个数。

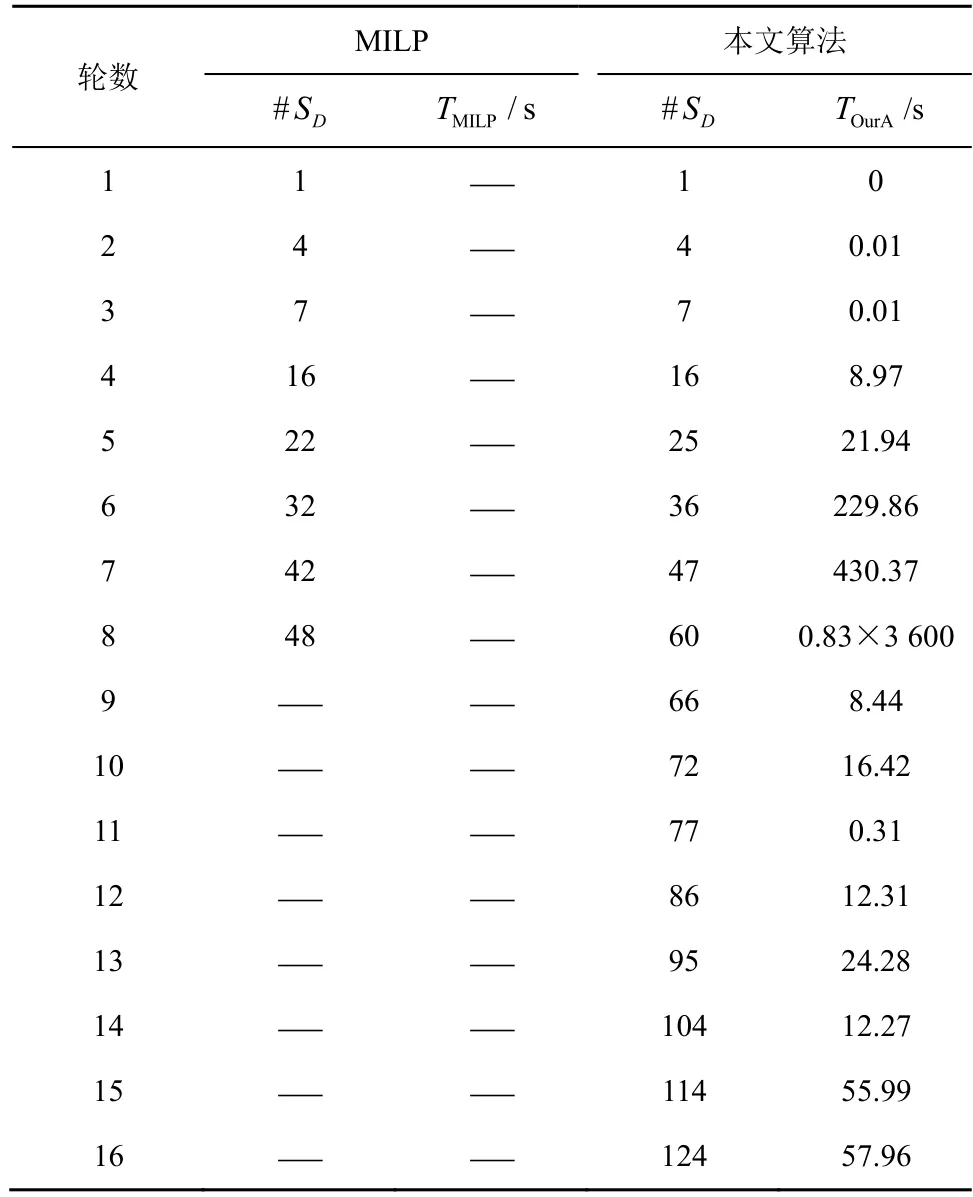
表4 FIDES 最小活跃S 盒个数

4 结束语

本文研究了分组密码常用的MDS 矩阵和二元域矩阵的差分和掩码传播性质，提出了差分模式分布表和掩码模式分布表的概念，证明了构造差分/掩码模式分布表的计算复杂度的下界，并给出了快速构造方法。基于Matsui 算法，提出了一种自动化搜索SPN 型分组密码最小活跃S 盒个数的快速算法，通过引入一些优化策略，极大提高了Matsui算法的效率。针对SPN 型分组密码LED、SKINNY、CRAFT 以及认证加密算法FIDES，给出了其全轮最小活跃S 盒个数。实验结果表明，本文算法的效率比基于MILP 的方法高。