The shadow and observation appearance of black hole surrounded by the dust field in Rastall theory

Xuan-Ran Zhu(朱轩然), Yun-Xian Chen(陈芸仙), Ping-Hui Mou(牟平辉), and Ke-Jian He(何柯腱)

1Chongqing College of Mobile Communication,Chongqing 401520,China

2Physics and Space College,China West Normal University,Nanchong 637000,China

3Department of Physics and Chongqing Key Laboratory for Strongly Coupled Physics,Chongqing University,Chongqing 401331,China

Keywords: Rastall gravity,black hole

1. Introduction

One hundred years ago,Einstein proposed the general relativity describing the gravity successfully. The existence of black holes and gravitational waves, as the two most important predictions in general relativity,has always attracted close attention of scientists. In 2015, the gravitational wave event(GW150914)generated by the merger of two black holes was detected by the Laser Interferometer Gravitational Wave Observatory (LIGO).[1–3]It is not only provides the first direct evidence for the existence of black holes,but also encourages people to uncover the mysterious veil of black holes. As another important milestone in the history of black holes, the image of the supermassive black hole in M87*convincingly confirms that the black hole exists in our universe. This ultrahigh angular resolution image comes from the international collaboration of Event Horizon Telescope (EHT).[4–7]From the image of the black hole, one can find that an asymmetric bright ring embedded in the dark background, in which,the bright ring is the photon ring,and the dark area inside the bright ring is called the shadow of black hole.

The strong gravity of black hole deflects light to form the shadow of the black hole,also known as the gravitational lensing effect. In 1966,Synge was the first to theoretically calculate the shadow of Schwarzschild black hole and the condition under which photons could escape to infinity was also given.[8]After that, the radius of photon ring for Schwarzschild black hole isr=5.2M(Mis the mass of black hole)was proposed in Ref. [9]. While for a rotating spherically symmetric black hole,i.e.,the Kerr black hole,the shape of shadow is decided by the rotating parameter,and the D-shape shadow can be obtained when the location of observer is fixed to the equatorial plane.[10,11]More research on black shadow can be seen in Refs.[12–40],the size and shape of the shadow for a rotating or non rotating black hole,and constraining black hole parameters with shadow have been studied in the general relativity and other modified gravitational backgrounds.

In our real universe, the black holes are surrounded by a large number of high energy radiative materials, which play an indispensable role in the observation of black hole shadow.[41]In 1979, the numerical simulation image of Schwarzschild black hole with the thin disk accretion was given by Luminet.[9]Taking into account the simplified model of accretion materials, that is, the black holes are obscured by the optically and thin spherically symmetric accretion,Narayanet al. pointed out the size of the observed shadow depends on the spacetime geometry and is not affected by the surrounding accretion.[42]While in Ref. [43], the shadow of a black hole is related to the geometrically thick accretion disks. Moreover, it can be found that the observation intensity of black hole shadow is significantly different in static and infalling accretion models.[44,45]Using the optically and geometrically thin disk accretion model, Grallaet al. found that the rings outside the black hole shadow can be divided into direct rings, photon rings and lensing rings.[46]And, the position and observation intensity of these rings are both closely related to the relevant parameters of spacetime and the position of thin disk accretion. So far, some research results of black hole shadow surrounded by the different accretion models have been obtained.[47–63]

As described in the studies,[64,65]Rastall proposed a possible modification of the general theory of relativity in 1972.According to the Rastall gravity theory, the covariant derivative of the energy momentum tensor is no longer zero in curved spacetime,whereby avoids the problem that the covariant conservation relation of the energy–momentum tensor is only verified in the Minkowaski flat or weak field regime of gravity.Based on the background of Rastall theory,Heydarzadeet al.obtained a new class of the Kiselev-like black hole solutions surrounded by perfect fluid, and they found that the corresponding effective complete fluid has different characteristics in different parameter ranges.[66]It means that Rastall parameter and surrounding field structure parameter can effectively describe the geometric structure of the spacetime. The physical characteristics of this class black hole models have also been studied, such as the thermodynamic behavior, quasinormal modes, and black hole shadow.[67–72]In Ref. [73], considering the black holes surrounded by perfect fluid radiation field in the Rastall theory, Guoet al. studied the shadow and observed luminosity of black hole. Nevertheless,the geometric effects of the Rastall parameters do not appear for the black hole surrounded by the radiation field.[66]In view of this, we focus primarily in this paper on the shadow and observed appearance of black hole surrounded by the dust field,where the Rastall geometric parameters exist. Due to the existence of Rastall geometric parameters,it can greatly change the causal structure of spacetime compared with the general theory of relativity. In particular,we want to study whether the change of the relevant parameters (the Rastall parameter and surrounding dust field structure parameter) will cause the change of shadow and photon sphere radius of black hole, or what kind of changes will be cause. In addition, we consider the emission form of the accretion material around the black hole is spherical symmetry,whereby to further study the influence of relevant parameters on the observed luminosity and appearance of black hole shadow,in these two accretion models.

The remainder of this paper is organized as follows. In Section 2,the black hole surrounded by the perfect fluid dust field in Rastall theory is briefly introduced,and the photon orbit and effective potential of the black hole are discussed. In Section 3,we show the shadow and photon sphere of the black hole in different spherical accretions, and the corresponding observed luminosity is also shown. We summarize results and discussions in the last section.

2. The black hole surrounded by dust field in Rastall theory and light deflection

Based on the hypothesis proposed by Rastall,[64,65]one can consider the Rastall field for a spacetime with Ricci scalarRand an energy momentum sourceTμν, which leads to the modification of the Einstein’s field equations as

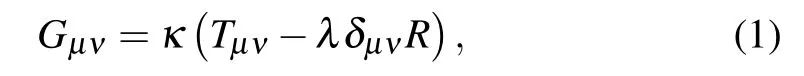
whereκis the Rastall gravitational coupling constant andλis the Rastall parameter,respectively. Note that the standard theory of general relativity can be traced back from Eq.(1)in the limit ofλ →0. Then,the solution of a general spherical symmetric black hole surrounded by perfect fluid in Rastall theory could take the form[66]

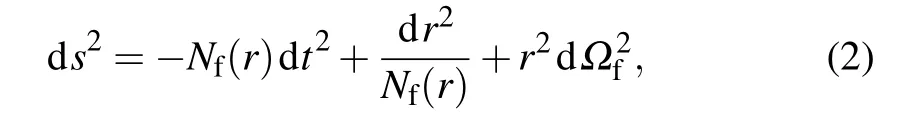
with

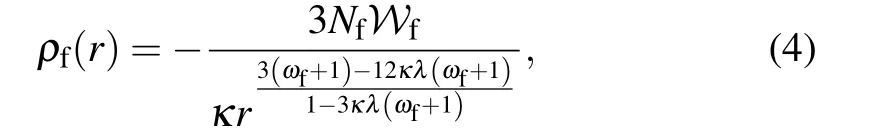
whereWfis a geometric constant depending on the Rastall geometric parametersκandλ,as well as the state parameter of surrounding fluidωf,that is

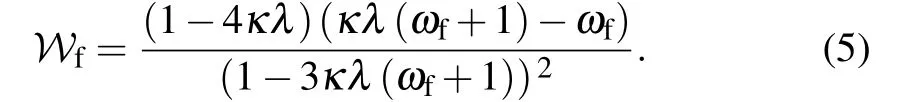
To preserve the weak energy conditionρf(r)≥0,WfandNfshould follow the condition

Hence,the sign of parameterNfis associated with each choice of the parametersκλ. By considering the black hole surrounded by a dust field in Rastall gravity, i.e.,ωf= 0, the metric function is given by[66,74,75]

In Eq. (7), the Rastall correction term is not expressed as the mass term,which also brings new characteristics to the black hole due to the existence of Rastall parametersκλ. Thus,the geometric parametersκλof the Rastall theory can play an important role in leading to distinct solutions relative to general relativity. It is worth mentioning that the value ofNdfollows the condition 0＜Ndfor the case of 0≤κλ ＜1/4,while forκλ ＜0∪κλ ＞1/4 it needs 0＞Nd. As we mentioned earlier,it is required that the weak energy condition represented by relation(6)is satisfied. Interestingly,there is an effective surrounding fluid accompanied by an effective equation of state parametersωefffor the case 1/6＜κλ ＜1/3,which explains the accelerating expansion of the universe in the Rastall theory of gravity, but the case violates the strong energy condition.In addition, the value of effective equation of state parameterωeffmay help to explain the deceleration expansion and even contraction of the universe whenκλvalues in the rang 1/6＞κλor 1/3＜κλ,which is conform to the strong energy condition.[66]

Since the wavelength of the actual light source is smaller than the size of the black hole,we can discuss the problem of black hole shadow in the scope of geometrical optics. That is,it is necessary to understand the motion behavior of photons in the spacetime near black holes. With the help of Euler–Lagrange equation, the motion equation of photon moving along geodesic can be expressed as

In the above equation,ξis the affine parameter, ˙xμis the fourvelocity of the light ray andℐis Lagrangian,respectively. In addition,we also can get

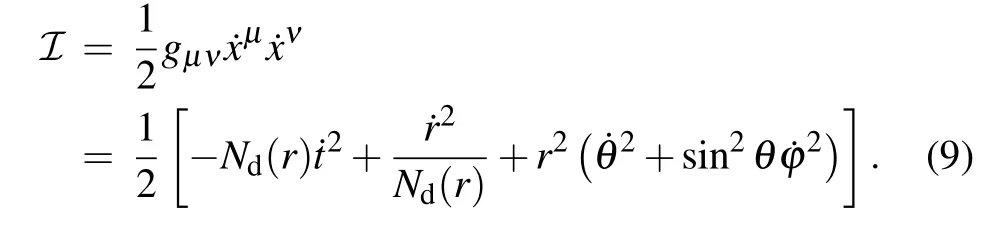
In the spherically symmetric space-time of Eq. (2), one can find that the metric coefficients do not depend explicitly on the timetand azimuthal angleφ. Hence, there are two conserved quantities, i.e., energyEand angular momentumL,which can be derived from the geodesic equations of the spacetime Eq. (2). In addition, we are most interested in the light ray that moves on the equatorial plane,which meansθ=π/2 or ˙θ=0.[56]Therefore,we can obtain

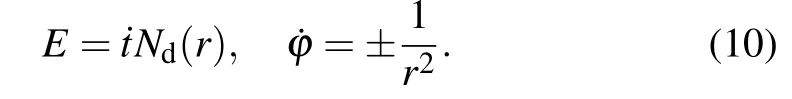
Substituting the above equations into Eq. (9), one can derive that

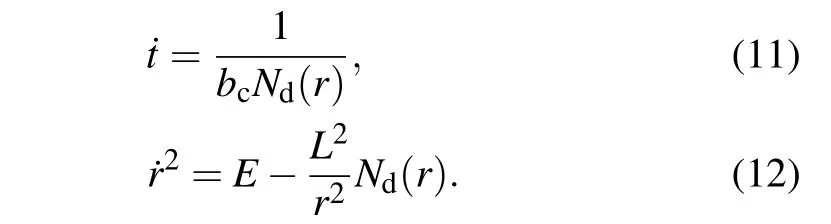
Here, we take a new affine parameterξ →ξ/|L|. It is worth mentioning that the impact parameterbc=L/E(the ratio of angular momentum to energy)is introduced,whereby we can succinctly describe the trajectory behavior of light. Using Eqs.(10)and(11),we can get the other form of Eq.(12),that is

Here,Veffis the effective potential of black hole, which is an important physical quantity to judge the deflection behavior of light around a black hole. Note that the critical one separating captured and uncaptured photons is given by the solution of the system ˙r2=0 and∂r˙r2=0,which means

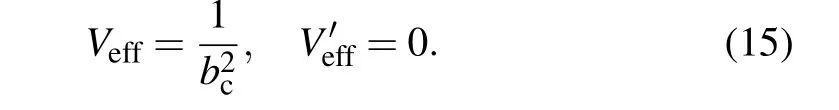
Naturally, the position of the photon ring can be obtained by Eq. (15), and the radius of the photon sphererpand impact parameterbpsatisfy

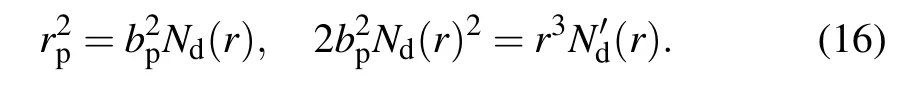
Supported by Eq. (16), we can obtain the radiusrp, and impact parameterbpof photon sphere under the different value of the geometric parametersκλand state parameterNdof the Rastall theory. For the different value of the parametersκλwhere the values ofNdis fixed,the numerical results of radiusrpand impact parameterbpof the photon sphere,as well as the event horizonreare listed in the Tables 1 and 2. For the case of parametersκλis fixed and the value ofNdis variable,they are shown in Tables 3 and 4.

WhenNdis a fixed positive value,one can see that the values of the radiusrpand impact parameterbpof photon sphere increases with the increase ofκλ,as well as the event horizonre. But in the case ofNdis a fixed negative value, the three physical quantitiesrp,bpandreare all smaller and smaller when the value of parametersκλis increase. For the case ofκλis fixed,rp,bpandreare also show an increasing trend with the positive growth ofNd, while decrease with the negative growth ofNd. That is, the black hole spacetime will expand with the increase of geometric parametersκλwhen the state parameterNdis positive, and the state parameterNdis negative has the opposite effect. It is worth noting that the change trend of relevant physical quantities is very weak whenNdis negative. We plot the effective potentialVeffcorresponding to the impact parameterbcwith the given value of geometric parametersκλand state parameterNd,as depicted in Fig.1.

Table 1. The radius rp, impact parameter bp of the photon sphere and the event horizon re for different geometric parameters κλ when Nd=0.05,in which,we take M=1.

Table 2. The radius rp, impact parameter bp of the photon sphere and the event horizon re for different geometric parameters κλ when Nd=-0.05,in which,we take M=1.

Table 3. The radius rp,impact parameter bp of the photon sphere and the event horizon re for different state parameter Nd when κλ =1/5,in which,we take M=1.

Table 4. The radius rp,impact parameter bp of the photon sphere and the event horizon re for different state parameter Nd when κλ =1/2,in which,we take M=1.

In Fig.1,we takeκλ=0.2 andNd=0.05 as an example.It shows the interior of the event horizon of black hole,namely,(r ＜rb),and there is no effective potentialVeff. However,the effective potential increases from the horizon and reaches its maximum at the position of photon sphere,and after that,there is a decreasing trend. Therefore, there are several different situations when a light ray moves in the radially inward direction. As the special case ofbc=bp, the light ray is in a critical state of being captured and escaping,and it will rotate around the black hole infinitely many times due to the angular velocity is not zero. This is corresponding to the region 2 (red lines) in Fig. 1. If the light ray motion at the region 1(bc＞bp)in Fig.1,the light will encounter the potential barrier and then be reflected back in the outward direction,that is,the photons in this region do not fall into the black hole and can reach the observer at infinity. When the light ray motion at region 3(bc＜bp)in Fig.1,which leads to the light ray through the event horizon and go straight into the black hole and the observer will not capture the light in this region. In order to explore the change of effective potentialVeffwhen the relevant parameters change, the effective potentialVeffof black hole under the different value ofκλandNdis shown in Fig.2.

From Fig.2(a),one can find that the peak value of the effective potentialVeffincreases with the decrease ofκλwhen the value ofNdis fixed(Nd＞0),and changes obviously.While the negativeNd(Nd＜0)has the opposite effect,i.e.,the peak value of the effective potentialVeffincreases with the increase ofκλ, but the degree of change is so weak that it can hardly be distinguished,as shown in Fig.2(b). In Figs.2(c)and 2(d),the value ofκλis fixed. The peak value of the effective potentialVeffalso decreases with the positive increase ofNdand the trend of change is also obvious. However, the peak value of the effective potentialVeffincreases with the negative growth ofNdwhenκλis fixed,but the trend of change is very weak.

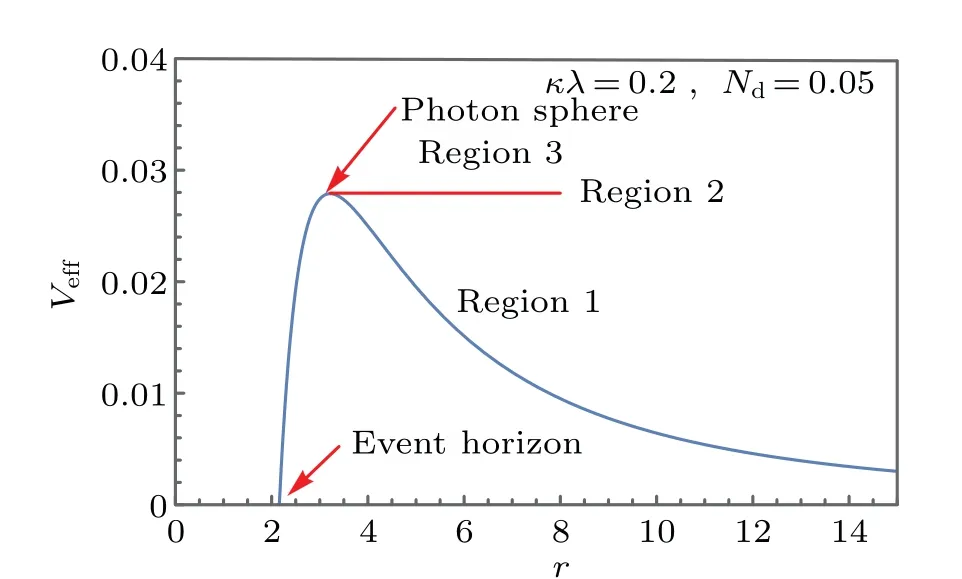
Fig.1. The profiles of the effective potential Veff as a function of impact parameter bc,in which κλ =0.2 and Nd=0.05. Here,we take M=1.

Fig.2. The profiles of the effective potential Veff as a function of impact parameter bc for the different value of κλ and Nd. (a) and(b) The value of κλ is various and the value of Nd is fixed(Nd=0.05 and Nd=-0.05). (c)and(d)The value of Nd is various and the value of κλ is fixed(κλ =0.2 and κλ =0.5). Here,we take M=1.

Fig.3. The trajectory of the light ray for the different value of κλ and Nd in the polar coordinates(r,φ),in which,the region of black hole is shown as a solid disk and the position of photon sphere as a dashed red line.

With the help of Eqs.(10)and(11), we can get the concrete expression of photon motion equation,which is

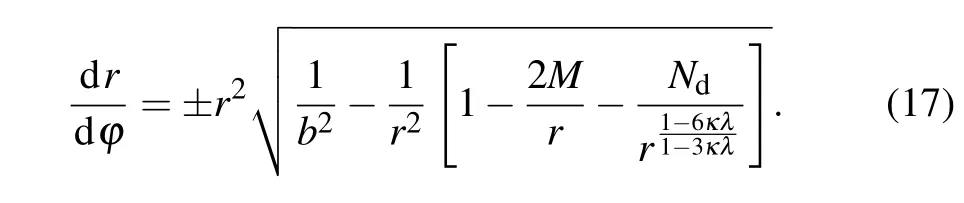
Here, we introduce a parameteru=1/r, and Eq.(17)can be rewritten as

Using the ray-tracing code,[42]we can plot the trajectory of the light ray for the different state parametersκλandNd, which are shown in Fig.3.

In the case ofbc＞bp(green lines), the trajectory of the light ray deflects,i.e.,the light ray move toward the black hole from infinity approaching one closest point and then move away from the black hole back to infinity. In the case ofbc＜bp(black lines), one can find that all the light ray falls into the black hole and cannot return to the observer’s position. In particular,bc=bp, which corresponds to the area of red dotted line, the light ray just revolve around the black hole,neither entering nor escaping from it,i.e.,the position of photon sphere. The key problem is to find the turning point where the light deflects owing to the light changing its radial direction, and the turning point corresponds to the minimally positive real root of Eq. (18). In Fig. 3, we can see that the trajectory and deflection of light near the black hole change with the different value of geometric parametersκλand state parameterNdin the spacetime Eq. (2). In other words, the light density that can be obtained by observers at infinity is different,which will naturally lead to the different observation appearance of black holes.

3. The shadows and photon spheres in different spherical accretions scenarios

With the previous preparations, we intend to further investigate the observed property and intensity of black hole shadow in the spacetime Eq.(2). In this section,we consider that thin spherical accretion is covered on a gravitating object,and two different models are given, i.e., the static spherical accretion and infalling spherical accretion.

3.1. The static spherical accretion

For the static spherical accretion model, it is considered that the accretion material is in a resting state,and the radiation of the material is isotropic. Hence, the intensity of radiationIobs(erg·s-1·cm-2·str-1·Hz-1) with the observed photon frequencyνobsfor the distant observer(ro→∞)can be taken as[76,77]

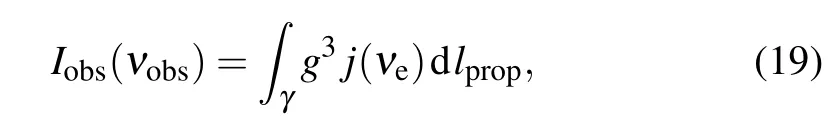
with

Here,g,νeandνoare the redshift factor, emitter photon frequency and observed photon frequency, respectively. In the rest frame of the emitter,j(νe) is the emissivity per unit volume,and dlpropis the infinitesimal proper length which is differential as measured in the frame comoving with the matter.In the spacetime Eq.(2),the redshift factor is

Considering a simple model that the radiation of light is monochromatic with a fixed frequencyνf,we can get

Note that Eq.(22)takes the radial profile as,andδis the delta function. Then,we can rewrite Eq.(23)as

On the basis of Eq. (17), the specific intensityIobs(νobs)observed by a distance observer is

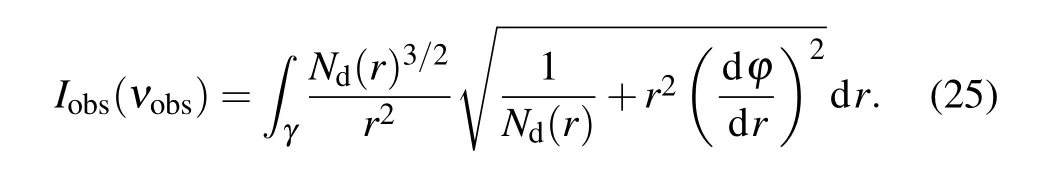
From Eq. (25), one can find that the observed luminosity of black hole shadow largely depends on the state parameters of the spacetime Eq. (2), as well as the impact parameterbc. It is worth mentioning that the intensity is circularly symmetric with the impact parameterbcof the radius, which satisfiesb2=x2+y2. Therefore, turn our attention to research the change of intensityIobs(νobs)with the impact parameterbcwhenκλandNdare taken as different values. In Fig. 4, we show the specific intensityIobs(νobs) as a function of impact parameterbcfor the different parametersκλandNd.

Fig.4. Profiles of the specific intensity Ibos seen by a distant observer for the static spherical accretion. (a)The value of Nd is various and κλ is fixed(κλ =0.2 and κλ =0.5). (b) The value of κλ is various and Nd is fixed(Nd=0.05 and Nd=-0.05). Here,we take M=1.

Fig.5. Profiles of the specific intensity Iobs seen by a distant observer for a static spherical accretion under the different relevant parameters(κλ and Nd).

Fig.6. Profiles of the specific intensity Iobs seen by a distant observer for a static spherical accretion under the different relevant parameters(κλ and Nd).

Obviously,although the parametersκλandNdare taken as different values, the observed intensityIobs(νobs) always reaches the peak at the position ofbc=bp. Since the light ray revolves around the black hole many times and collects an arbitrarily large intensity, the intensity increases sharply and reaches the peak value. For the case ofbc＞bp, the intensity of observer is mainly contributed by the refracted light,so that the intensity decreases with the increase ofbc. If the value ofbcis large enough,the refracted light tends to disappear,which thus leads to the vanishing of observed intensity. Due to the intensity originating from the accretion is absorbed mostly by the black hole in the case ofbc＜bp,the observers rarely capture intensity. However,there is a part of the radiation escaped from the black hole. Hence, the specific intensity does not disappear completely with a small finite value.

Furthermore, the different parameters ofκλandNdwill cause the observer to obtain different observation intensitiesIobs(νobs). When the parametersκλare given,the observation intensity will decrease with the positive growth of parameterNd, and the degree of weakening is very obvious. While the observation intensity will increase with the negative growth of parameterNd,but its growth degree is very small,which leads that we can not clearly distinguish the dotted line in Fig.4(a).When the parameterNdis fixed as a positive value,the increase of parameterκλwill also significantly weaken the observation intensity. In the case ofNdtaken as a negative value, the increase of parameterκλpromotes the observation intensity,but the increase degree is so small that the dotted lines is shown almost superposed in Fig. 4(b). In order to make our result more visible,we show the shadow images and the corresponding intensities as seen by a distant observer for the different values of parametersκλandNd,and shown in Figs.5 and 6.

From the top row of Fig. 5, one can see that for a given value of parametersκλ(κλ=0.2),the shadow size increases with the larger value ofNd, but the observed intensity decreases. In the bottom row of Fig.5,the parametersκλ=0.5 andNdshow a negative growth trend,and not only the change of the observed intensity is very weak, but also the radius of the shadow has small change. As shown in the top row of Fig. 6, the observed intensity has been weaken with the positive increase of parametersκλ, but the shadow radius of the black hole shows the opposite trend. In the bottom row of Fig.6,the change of both shadow radius and observed intensity are weak with the change ofκλ,where the parameterNdis fixed as a negative value.And the impact of change ofκλis almost nil. Hence,the state parametersκλandNdplay an important role for the observed intensity,and the change of those values will directly affect the observed intensity of the distant observer.

3.2. The infalling spherical accretion

In this section, we start with a more realistic model, i.e.,the optically thin accretion moves towards the black hole,due to the most accretion matters in the universe should not be static. Here, the optically thin accretion is considered to be infalling matters, which is a real accretion flow process. For simplicity,we also take the radiation power and emission coefficient,as measured in the rest frame of the infalling accretion.Along the way, the velocity of the infalling accretion will affect the redshift factor of accretion. And the redshift factor of infalling accretion can be expressed as[47]

wherekμ=is the four-velocity of the photon. In addition,is the four-velocity of the accreting matter emitting the radiation,and=(1,0,0,0)is the four-velocity of the distant observer. We assume that the accretion matter in radial is free and falls with the four-velocity,which in the spherically symmetric case of spacetime Eq.(2)reduces to

For the photons,the four-velocity was found in Eqs.(10)–(12).With the constant ofkt=1/bcandkγkγ=0,we can getkγas

where the sign + (-) indicates that the photon approaches(goes) away from the black hole. The redshift factor in Eq.(26)is given by

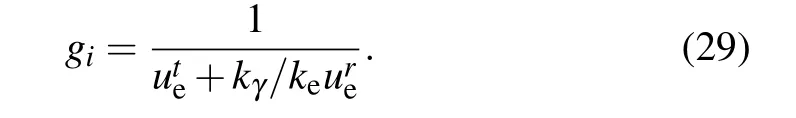
Then,the proper length dlpropcan be written as

in which,ξis the affine parameter along the photon pathγ,andλhas to be evaluated along the path of the photon. Integrating the intensity over all the observed frequencies, we obtain the observed flux,that is

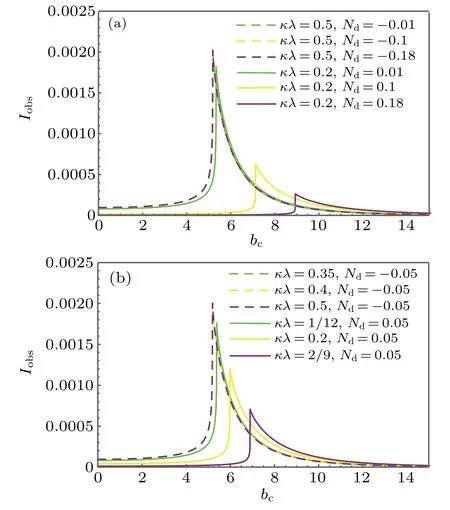
Fig.7. Profiles of the specific intensity Iobs seen by a distant observer for the infalling spherical accretion. (a)The value of Nd is various and κλ is fixed (κλ =0.2 and κλ =0.5). (b) The value of κλ is various and Nd is fixed(Nd=0.05 and Nd=-0.05). Here,we take M=1.

Now,we still take different value of geometric parametersκλand state parametersNdfor investigating the shadow of the black hole with an infalling accretion,as shown in Fig.7.From Fig.7,the peak value of luminosity is much lower than that of static accretion model, which is the most significant difference for both the static and infalling accretion models.Moreover, there is a sharp rise before the luminosity reaching its peak for the infalling spherical accretion models, i.e.,the change rate of intensity of the infalling accretion is greater than that of static accretion.It shows that the absorption rate of photons by black holes is higher than the static case.When the value of parametersκλincrease andNdis fixed as a positive value(orκλis fixed andNdis positive growth),the peak values of luminosity showed an obvious downward trend. While for the parameterNdis negative value and parametersκλincrease(orκλis fixed andNdis negative growth),the peak values of luminosity will increases but the change is very small.

In addition,the corresponding two dimensional images of the intensity are drawn in Figs.8 and 9. Comparing with the static case, the central region for the infalling case is darker,and the light intensity that the observer can obtain is much smaller. This is caused by the Doppler effect here. However,the radius of the shadow and the position of the photon sphere are consistent under the different accretion (the static and infalling spherical accretion), which means that the different accretion model affect the observable intensity of shadows but does not affect the geometry structure of spacetime.

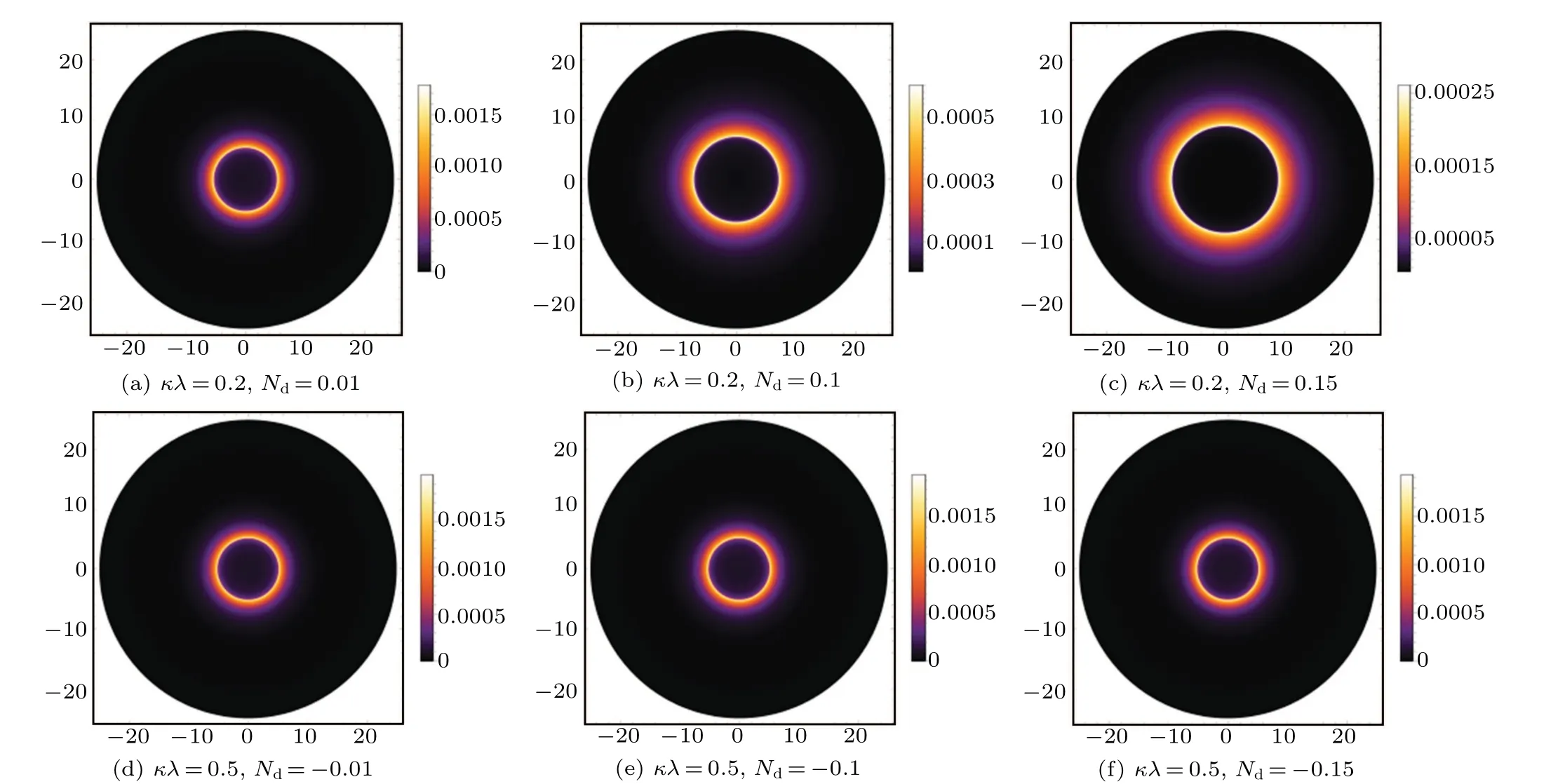
Fig.8. Profiles of the specific intensity Iobs seen by a distant observer for a static spherical accretion under the different relevant parameters(κλ and Nd).

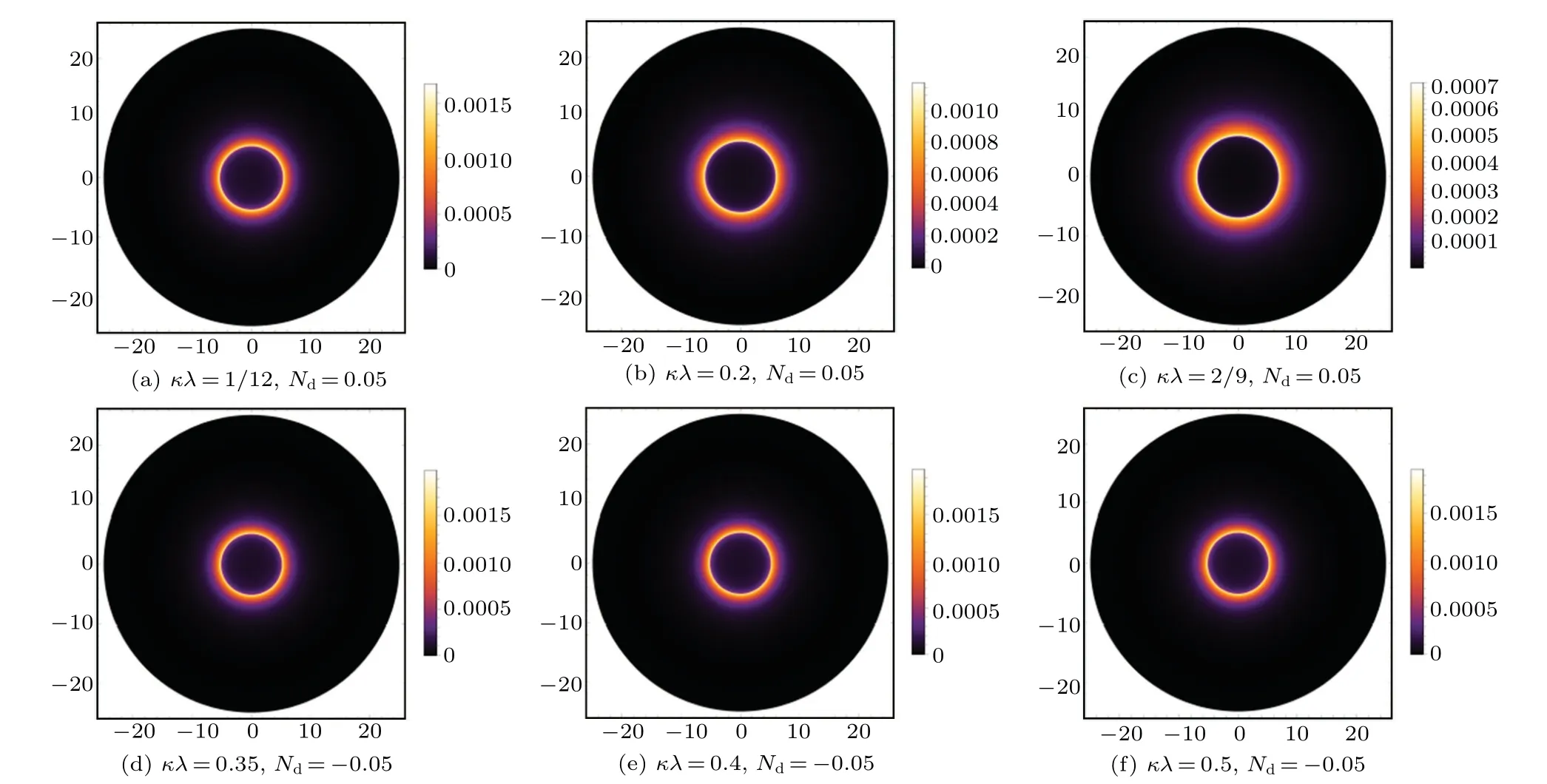
Fig.9. Profiles of the specific intensity Iobs seen by a distant observer for a static spherical accretion under the different relevant parameters(κλ and Nd).

4. Discussion and conclusion

In the scenario of Rastall gravity theory,the shadow and observation appearance of black hole immersed in dust field have been studied in detail. It is shown that the radius of event horizonre,photon spherere,and critical impact parameterbpof the black hole have interesting characteristics depending on the different ranges of the parameters in Rastall theory.Specifically,these three related physical quantities all show a significant increase as the increase of Rastall geometric parametersκλ,where the field structure parameterNdis given,as well as the case ofNdincreases where the value ofκλis fixed. But if the parametersκλincrease andNdis a fixed negative value,or the parametersκλare fixed andNdis negative growth,both the physical quantitiesre,rpandbpwill show weak decreasing trend. Naturally, the increase ofκλ(Ndis fixed as a positive value) or the positive growth ofNd(κλis fixed) will significantly reduce the peak value of effective potential. While the parameterNdis negative(or is negative growth),it has a positive effect on the effective potential.

When the values of Rastall geometric parametersκλand state parameterNdchange, it can be found that not only the shadow radius of the black hole changes, but also the deflection degree of light ray near the black hole changes.Therefore,the light density that can be obtained by an observer at infinity is different, which will naturally lead to the different observation appearance and intensity of the black hole shadow. In order to intuitively reflect the change of shadow observation characteristics caused by the change of relevant parameters(κλandNd), we calculate the specific intensity observed by an infinite observer, and also give the profile image of black hole shadow in different relevant parameters. In system (7),we consider that the accretion radiation is the only background light source, and mainly take two accretion models, i.e., the static and infalling spherical accretions, which are optically and geometrically thin.

For the case of static spherically accretions,the inner region of the black hole shadow is not completely dark,and the peak of observed intensity is always near the position of the photon sphere. One can find that the peak of observed intensity is attenuated with the increase of parametersκλin the case of parameterNdis fixed as a positive value, while is enhancement with the increase of parametersκλin the case of parameterNdis fixed as a negative value. When parameterκλis taken as a fixed value, the peak value of observation intensity will decrease with the positive growth of parameterNd,but increase with the negative growth ofNd. For the case of infalling spherical accretion, the change trend of observation intensity caused by the change of relevant parameters is similar to that of static model,but the change degree is greater than that of static model. Meanwhile, both the inner region and the outer observable bright region of the black hole shadow are obviously darker than the static accretion model. And the peak value of the observed intensity is about two orders of magnitude lower than that of the static model. Doppler effect is the reason for the significant difference of observation intensity between these two different accretion modes. For different spherical accretions background, the weakening of observation intensity caused with the variation with parameters(κλandNd)is very obvious,but the degree of enhancement is very weak. As shown in Fig.4 for the static model(Fig.7 for the infalling model), the dotted lines almost coincide and the change of peak value is very weak,which can also be reflected from the bottom row of Figs. 5 and 6 (Figs. 8 and 9 for the infalling model). The increase extent of observation intensity is very weak and can even be ignored. Moreover,the size and position of black hole shadow do not change in the both case of accretion models. It is implied that the black hole shadow is caused by spacetime geometry,which is determined by the geometric parametersκλand state parameterNdin the background of Rastall gravity theory. Put forward, it could be a feasible method to explore the structural parameters of spacetime from the observation of black hole shadow.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.11875095 and 11903025)and Basic Research Project of Science and Technology Committee of Chongqing(Grant No.cstc2018jcyjA2480).