TDoA 定位盲区分析与节点部署策略研究

赵越，李赞，李冰，郝本建

（1.西安电子科技大学通信工程学院，陕西 西安 710071；2.中国人民解放军31007 部队，北京 100000）

0 引言

无线传感器网络（WSN,wireless sensor network）能够实现对覆盖区域内非合作信号源的感知、识别、定位等功能[1]。非合作信号源的定位一般包含2 个步骤：定位参数估计和信号源位置解算[2]。具体来说，各个传感器节点将采集的信号原始数据回传至融合处理中心，后者从多组接收信号数据中提取出关于信号源位置的定位参数。在此基础上，融合处理中心根据定位参数和各个传感器节点自身的准确空间位置信息，构建信号源位置信息关联方程组并求解。常用的定位参数包括到达时间（ToA,time of arrival）、到达时间差（TDoA,time difference of arrival）、到达频率差（FDoA,frequency difference of arrival）、到达角度（AoA,angle of arrival）等[3-5]。

在基于接收信号参数测量实现信号源定位的WSN 中，信号源的空间位置是根据定位参数及传感器节点自身位置计算得到的。因此，WSN 对信号源的定位精度取决于各个传感器节点的接收信噪比、WSN 相对于信号源的空间几何构型、WSN的系统误差（包括节点位置误差、时钟同步误差等）[6]。接收信噪比受信号源的辐射强度、信号传输距离、传感器节点感知能力等多种因素影响，它直接决定了WSN 对定位参数的估计精度。WSN和信号源所构成的空间几何构型决定了WSN 对信号源的空间辨识度，并由此决定了信号源位置关联信息。系统误差影响了定位参数与真实信号源位置的关联准确度，可等效为定位参数估计误差和传感器节点自误差，继而在位置解算时产生定位误差。

在定位精度的影响因素中，通过增强节点感知能力或物理空间上靠近信号源，可以提升各传感器节点的接收信噪比；通过标校站辅助或系统误差统计数据，可以消除系统误差。然而，空间几何构型是由位置未知的信号源与WSN 中各节点的位置共同决定的[7]。当WSN 与信号源所构成的空间几何构型较好时，WSN 对信号源的空间辨识度较大，能够提供的空间域信息较多；反之，能够提供的空域信息较少，导致定位精度严重恶化，产生定位盲区。需要说明的是，无线定位中盲区与无线通信中盲区的产生原因是不同的，前者是由于传感器网络对信号源的定位几何构型恶化或消失，而无法区分目标的空间位置，与接收信噪比没有直接关系；后者则是由基站覆盖区域、障碍物遮挡、通信网络拥塞、信号频段特性等因素造成用户接收情况恶化，进而影响通信服务质量[8-10]。

国内外学者对定位盲区进行了阐述与分析[11-15]。文献[11]提出TDoA 与FDoA 联合定位算法，并在仿真算法性能时发现，当信号源位于定位节点连线方向时无法准确定位。文献[12]对TDoA 与FDoA 定位场景中的定位精度分布进行了分析，并定义了定位有效区域与定位无效区域（即定位盲区）。为了解决TDoA 与FDoA 定位场景中的定位盲区问题，文献[13]提出引入AoA 作为辅助定位信息的思路及相应算法。文献[11]论证了利用TDoA 和FDoA 实现信号源定位时的克拉美罗下界（CRLB,Cramer-Rao lower bound）等高线与仅利用TDoA 定位时的CRLB 等高线具有相同的分布，即TDoA 定位中在定位节点连线方向存在定位盲区。在基于TDoA 的二维定位场景中，文献[14]研究了定位节点分布对定位精度的影响。在基于TDoA 的三维定位场景中，文献[15]研究了基线长度、基线角度、传感器节点高程、传感器平面等多种因素对覆盖区域定位精度分布的影响，并通过仿真分析得出了定位盲区所在的分布区域。此外，文献[16]论证了在基于AoA 的定位场景中，当定位节点相对于信号源位于同一方向时，交叉定位结果将急剧恶化并产生定位盲区。

然而，现有文献对定位盲区的分析仍然具有局限性。当定位节点相对于信号源的空间几何构型确定时，现有文献通过仿真结果证明了定位盲区的存在，并简要分析了定位盲区的出现区域，但未从数学角度深入剖析定位盲区的产生原因，也未能给出判断及预测定位盲区所出现区域的方法。此外，现有文献并未阐述当测量矩阵满秩时定位盲区的产生条件以及出现区域。

定位节点部署策略是定位网络空间几何构型优化的主要技术手段。现有文献大多针对单一信号源进行定位节点部署策略研究，在已知信号源准确位置的前提下，给出最优的节点部署策略。文献[17]研究了二维TDoA 定位场景中最优的节点部署策略，从CRLB 对定位节点方位角的驻点入手，推导出等角度阵列（UAA,uniform angular array）是使信号源CRLB 最小的部署方案。Yang等[18-20]研究了TDoA 定位中的传感器节点部署策略，推导证明了针对单一信号源的最优部署方式是UAA，并提出存在部署区域约束时定位精度最优化的节点部署策略。

在研究面向整个覆盖区域的WSN 节点部署策略时，现有针对单信号源的部署策略不再适用。文献[15]仿真分析了当传感器所在平面与信号源方向成不同夹角时定位盲区的分布区域，并提出应尽可能使信号源位于传感器所在平面中心点的法线方向，然而，该文只是粗略地给出了避免定位盲区时应具有的条件，未能给出最优的部署方案。文献[21]提出定位精度门限的概念，并将WSN 覆盖区域中定位精度优于该门限的区域视为有效定位区域。继而将最大化有效定位区域为优化目标，通过仿真分析生成若干组具有不同构型的定位网络，寻求使有效定位区域面积最大的一组定位节点。然而，该文只分析了有限的定位节点构型组合，未能给出最优的定位节点部署方案。

本文以基于TDoA 定位参数的二维WSN 为基本场景，开展TDoA 定位盲区分析与节点部署策略研究。首先，从定位误差的理论界限CRLB的角度出发，对定位盲区的产生原因进行了剖析。其次，分析了TDoA 测量误差、WSN 相对于信号源的空间几何构型等不同因素对定位盲区的影响。再次，提出了平均CRLB 作为衡量WSN 覆盖区域定位精度的表征方式；在此基础上，以平均CRLB 为目标函数，构建了传感器节点部署优化问题，并提出了基于定位盲区预判断的遗传算法对其求解。最后，计算机仿真验证了单信号源定位时CRLB 的性质；验证了定位盲区与信号源相对于传感器节点的方向向量有关，且会出现在满秩测量矩阵的场景中；验证了所提节点部署算法对于WSN 覆盖区域的定位精度优于3 种基准算法。

1 TDoA 定位场景及定位精度衡量参数

1.1 二维TDoA 定位场景

基于无线传感器网络实现非合作信号源定位场景如图1 所示。WSN 包含M(M≥3)个节点，节点位置坐标的集合为{s1,s2,…,sM}T，其中，,∀i=1,2,…,M。U为WSN 的覆盖区域。在U内存在一个信号辐射源，其位置坐标为。从WSN 的角度来说，该信号源是非合作的，即WSN 无法掌握该信号源的先验信息，例如信号辐射时刻、信号参数特征、历史运动轨迹等。因此，WSN 采用基于TDoA 参数的定位方式，不需要与非合作信号源进行交互即可实现对其位置估计。

图1 非合作信号源定位场景示意

假设信号源和无线传感器节点之间为直射路径，则信号源所辐射的无线电波传播至第i个传感器节点的时间为

其中，c为无线电波的传播速度，为向量的2 范数运算。

不失一般性，将节点s1视为测量TDoA 时的参考节点，则信号源的辐射信号传播至第i个节点和参考节点的真实时间差为

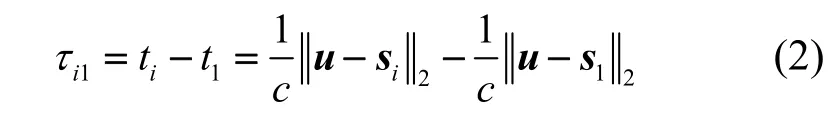
考虑高斯加性噪声的TDoA 测量模型，通过接收信号相关运算测量得到的信号源的TDoA 为

其中，为TDoA 测量值，ni1服从均值为零、方差为的高斯分布。

定义TDoA 测量值集合和测量误差的集合分别为

其中，n服从均值为零、协方差矩阵为的高斯分布，d ing{x}表示将向量x作为对角元素的矩阵。

1.2 单信号源定位精度衡量参数

信号源的位置解算过程就是按照某一准则从TDoA 测量值中估计出信号源的位置坐标，并尽可能地使其接近其真实位置u。作为任何无偏估计的方差下界，基于信息理论的CRLB 在定位问题中被广泛地作为定位精度的衡量参数，CRLB 定义为费希尔信息矩阵（FIM,Fisher information matrix）的逆矩阵[4]。

在基于TDoA 的定位场景中，利用τˆ 对信号源位置u进行估计时的CRLB 为

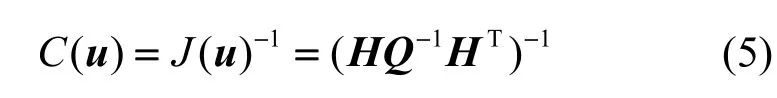
其中，C(u)为CRLB，J(u)=HQ-1HT为FIM。矩阵H取决于信号源u和WSN 中各节点的空间位置关系，其每一列是TDoA 真值（标量）对于信号源真实位置（列向量）的导数，具体表达式为

其中，di1,x、di1,y分别为向量di1的横、纵坐标。由于C(u)是J(u)的逆矩阵，根据 FIM 的行列式det(J(u))与伴随矩阵J*(u)可进一步得到C(u)的表达式，即

进一步地，可得TDoA 定位场景中信号源位置估计的CRLB 的迹为

根据式(4)～式(10)，可以得到以下关于CRLB的若干性质。

性质1当TDoA 误差的方差恒定时，CRLB与信号源到各节点的距离无关。

证明在式(5)中，若矩阵Q恒定，则CRLB 只与矩阵H有关。根据式(6)中矩阵H的表达式可知，H仅与信号源到达各节点的方向向量有关，而与信号源和各节点的距离无关。此外，根据式(10)也可以得到相同结论。证毕。

性质2在TDoA 定位中，将任一节点视为参考节点对CRLB 没有影响。

证明性质2 的证明可参考文献[4]，该文献分析了TDoA 和FDoA 联合定位场景中参考节点选择的无关性。需要说明的是，若融合处理中心准确已知各节点的接收信噪比，那么参考节点和其他节点测量得到的TDoA误差分布特性是可计算得到的[6]，当改变参考节点时，CRLB 是不变的。证毕。

2 定位盲区存在性及影响因素分析

定义1若WSN 对某一信号源的CRLB 趋于无穷大，则称信号源所处的空间位置为WSN 的定位盲点。

定义2在WSN 的覆盖区域内，全部定位盲点的集合称为WSN 的定位盲区。

由式(10)可知，WSN 相对于信号源的空间几何构型影响着定位精度衡量参数CRLB。当几何构型较好时，CRLB 较小，WSN 可实现对信号源的精确定位；反之，CRLB 较大甚至趋于无穷，WSN 对信号源的定位误差极大，甚至失效，此时认为该信号源所处位置位于WSN 的定位盲区内。

定理1在基于TDoA 的二维定位场景中，若传感器节点相对于信号源的方向向量组中，不同向量的个数不大于2，则信号源所处位置为WSN 的定位盲点。从数学表达式的角度来说，信号源u相对于全部传感器节点{s1,s2,…,sM}的方向向量为{d1,d2,…,dM}，若{d1,d2,…,dM}满足以下任意一种情况时，WSN 对于该信号源的CRLB 不存在。

情况1 所对应的定位几何构型是全部M个节点和信号源共线，且均位于信号源的同一侧。情况2 表示存在2 个不同方向向量，而其余方向向量均等于其中之一，所对应的定位几何构型是全部M个节点均位于相对于信号源的2 个不同的方向向量上。

证明根据柯西-施瓦茨不等式的一般形式可知，式(10)的分母是非负的，即

当柯西-施瓦茨不等式中等号成立的充要条件满足时，式(10)的分母为零，tr(C(u))不存在，产生定位盲区。式(11)取等号的充要条件为

下面讨论式(12)成立的条件。

2) 若di1≠0 且d21,…d(i-1)1,d(i+1)1,…,dM1=0，则式(12)成立，此时方向向量d1,d2,d i-1,di+1…,dM均相等，且与di1不相等，所对应的定位几何构型是除si外其余传感器节点和信号源共线，且信号源位于这些节点的一侧，如图2(b)所示。

3) 若di1≠ 0且d21,…d(i-1)1,d(i+1)1,…,dM1=di1，则式(12)成立，此时除d1外，全部方向向量均与di相等，所对应的定位几何构型是除参考节点s1外其余传感器节点和信号源共线，且信号源位于这些节点的一侧，如图2(c)所示。

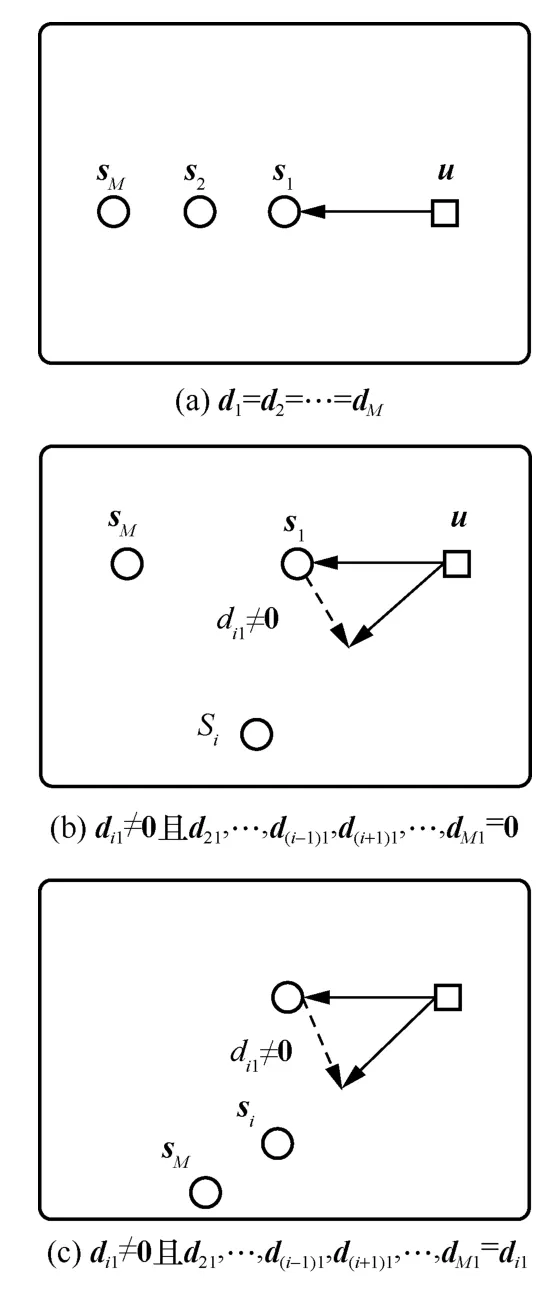
图2 定位盲区产生条件的示意

4) 若di1≠ 0,dj1≠0,i≠j，则不存在λ使式(12)成立。

证毕。

推论1在二维TDoA 定位场景中，当传感器节点排列为线形阵列时，节点所在直线为定位盲区；当存在一个传感器节点与其余节点不共线时，传感器节点包围的区域内不存在定位盲点，包围区域一定不是定位盲区。

证明当传感器节点排列为线形阵列时，若信号源位于传感器节点连线在某一侧的延伸线上，则定理1 中的情况1 成立，该位置为定位盲点；若信号源位于传感器节点之间，则定理1 中的情况2 成立，该位置为定位盲点。综上，当传感器节点排列为线形阵列时，节点所在直线为定位盲区。

另一方面，当存在一个传感器节点与其余节点不共线时，节点包围区域内的任意一点（即使在任意2 个传感器节点的连线上）相对于全部传感器节点的相同方向向量个数都严格大于2，因此包围区域内不存在定位盲点。证毕。

推论2TDoA 测量误差的强度并不影响定位盲区的存在，以及定位盲区所处的空间位置。

证明定理1 阐述的2 种定位盲点存在情况均与TDoA 测量误差的强度无关，只与WSN 相对于信号源的空间几何构型有关。因此，即使TDoA 定位误差的方差逐渐变小，也依然存在定位盲区，且所处空间位置不变。证毕。

推论3在3 个传感器节点构成的WSN 中，定位盲区存在于任意2 个传感器节点连线的外侧。

证明当仅存在3 个传感器节点且不共线时，根据推论1，传感器节点内侧包围区域一定不是定位盲区。然而，当信号源位于任意2 个传感器节点的外侧连线上时，定理1 的情况2 满足，外侧连线对应的区域为定位盲区。证毕。

根据定理1 及相关推论，可以定性分析WSN 覆盖区域中的定位盲区，继而指导WSN 的部署方案、定位盲区的补盲方案、信号源定位结果的置信度评估等。具体来说，在典型场景中部署WSN 时，应使定位盲区远离重点监测区域及目标信号源，从而保证定位精度。其次，借鉴无线通信中的微蜂窝、直放站等补盲方式，以定理1 为理论支撑，通过部署额外的节点可消除定位盲区。最后，在信号源定位过程中，若连续定位结果在区域内剧烈跳变，且多个定位点处于WSN 的定位盲区内，则定位结果的置信度较差。

推论4对于某一定位网络和信号源形成的矩阵H，若该矩阵的秩小于空间维度，该信号源处于定位盲区。

证明对于定理1 中的情况1，矩阵H的列向量全部为零向量，此时该矩阵的秩为0；对于定理1中的情况2，矩阵H的全部列向量是平行的（考虑存在零向量的情形），如图2(b)和图2(c)所示，此时，该矩阵的秩为1。因此，若矩阵H的秩小于空间维度，该信号源处于定位盲区。证毕。

3 基于平均CRLB 的传感器节点部署算法

定位盲区的产生与WSN 的部署方式紧密相关，一旦出现定位盲区，WSN 所覆盖区域的平均定位精度将急剧恶化。因此，面向重点监测区域部署WSN 时，应以避免定位盲区为首要目标。本节首先提出区域定位精度的衡量参数，并以此为基础构建节点部署优化问题，提出基于定位盲区预判断的遗传算法进行求解。

3.1 区域定位精度衡量参数

定义3若信号源随机出现在WSN 的覆盖区域U中，其位置坐标服从概率密度函数f(u)，则WSN 对于信号源的平均CRLB 为

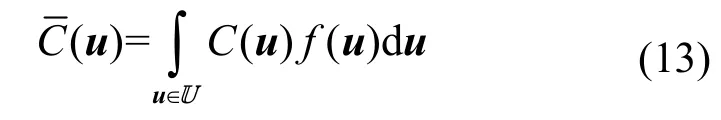
其中，积分区间是u∈U。如式(10)所示，C(u)与u呈高度非线性关系，难以直接给出平均 CRLB的表达式。因而，本文采用离散形式逼近平均CRLB。

定义4在覆盖区域U中，按照概率密度函数f(u) 随机生成N个信号源，即{u1,u2,…,uN}，则平均CRLB 可近似为

其中，pi是信号源出现在第i个位置时的概率，均匀分布时。当N→∞时，

说明如下。1) 覆盖区域的定位精度还可以使用定位中断概率来衡量，类似于文献[21]提出的有效定位区域的概念。然而，平均定位精度更适合于衡量存在定位盲区时的区域定位精度，这是因为中断概率中的定位精度阈值难以合理设定。2) 对于非合作信号源，其出现在WSN 覆盖区域的概率密度函数是未知的，此时假设f(u) 为均匀分布是合理的。3)C(u)与信号源位置u和传感器节点的位置{s1,s2,…,sM}有关，而(u)与按照随机变量u概率密度函数随机产生的N个采样点位置{u1,u2,…,uN}和传感器节点的位置{s1,s2,…,sM}有关。

3.2 节点部署优化问题构建与分析

在传感器节点部署时，需要提前规划各个传感器节点的部署位置，从而实现对WSN 覆盖区域内潜在信号源的最优定位精度。本文以平均CRLB 为目标函数，构建约束优化问题为

需要说明的是，针对单一信号源的节点部署方式，文献[17]已证明均匀角度部署是最优的。而在优化问题 P1中，目标函数是整个区域内随机选取采样点后计算得到的平均CRLB，因此该优化问题的最优解应该是使区域平均定位精度最好的一种部署方式。

由式(10)可知，WSN 对单个信号源的CRLB 是关于传感器节点空间位置向量的非凸函数。进一步地，在式(15)中，目标函数C～(u)的表达式关于待求解变量也呈现出非凸性质。因而，想要直接求解优化问题 P1较为困难。

3.3 直接遗传算法和基于定位盲区预判断的遗传算法

遗传算法是一种较成熟的进化算法，在资源分配、网络规划等领域的大量非线性和非凸的优化问题中被广泛应用[22-24]。遗传算法的核心思想来源于达尔文的生物进化论，通过模拟生物进化过程中的自然选择、种群繁殖、基因突变，利用“种群”的不断进化和淘汰，最终实现优势个体的保留和劣势个体的移除[25]。

3.3.1 直接遗传算法

本节采用遗传算法直接求解优化问题 P1，将目标函数、决策变量映射为遗传算法的基本元素，具体如下。

环境适应度。优化问题中的约束条件仅包括传感器节点的定义域，无其他约束条件，因此环境适应度函数可直接选取目标函数，即，其中δ是使分母不为零的极小自然数。

下面给出利用遗传算法求解优化问题 P1的主要步骤。

步骤3采用联赛选择算法或轮盘赌选择算法对当前种群进行选择，尽可能保留适应度函数较大的个体，并抛弃适应度函数较小的个体。联赛选择算法的思想是随机挑选k个个体进行竞争，适应性最好的将获得遗传权。轮盘赌选择算法的思想是将适应度与选择概率联系起来，个体被选中的概率与其适应度大小成正比。

步骤4利用基因重组的思想，产生现有种群中个体的后代，使个体数量恢复到Np。例如，对于个体和，其后代可按照获得，其中，l服从均匀分布U(0,1)，⊙为向量的Schur 积。

步骤5利用基因突变思想，对种群中一定比例的个体的染色体进行随机变化。基因突变可保证种群的多样性，避免算法陷入局部最优解。

步骤6判断迭代次数是否达到预设值，若达到预设值则算法结束，返回当前最优解；否则返回步骤2，且迭代次数加1。

3.3.2 基于定位盲区预判断的遗传算法

在直接遗传算法中，决策变量是WSN 中各节点的空间位置坐标，因此每个染色体χ中包含2M个未知标量；此外，在遗传算法的迭代过程中，种群在整个定义域内进行更新。因此，直接遗传算法具有较大的运算复杂度，且只能求解得到优化问题 P1的近似最优解。

根据推论1，若信号源处于WSN 的部署范围S内，传感器节点应尽可能地部署在该区域的外部边界，且尽可能地避免多个传感器节点共线，由此可避免定位盲区，降低区域的平均定位误差。因此，若S为凸集，可以将 P1中的决策变量修改为

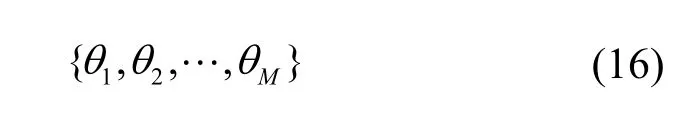
其中，θi表示第i个传感器节点相对于S内任一参考坐标原点（例如s0）的方位角，即

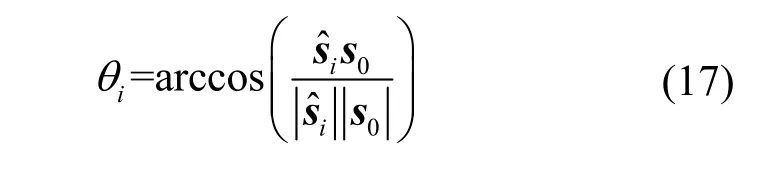
由于S为凸集，则方位角与位置坐标可一一对应，可以将节点部署优化问题改写为 P2，即

在 P2中，将 {θ1,θ2,…,θM}所对应的位置坐标约束在部署区域的外部边界，这样的约束条件设置内在地避免了定位盲区的产生，从而保证了区域的平均定位精度，因此优化问题 P2的解可进一步逼近最优节点部署方案。

为了对比算法复杂度，本文给出如下定义。定义算法在单个个体迭代中花费的时间为tf=tfitness+tselection+tcrossover+tmutation，其中，tfitness表示计算环境适应度函数的时间成本，tselection、tcrossover、tmutation分别表示执行选择、重组、突变的时间成本。定义可允许的最大进化迭代次数为Lmax，则遗传算法的时间复杂度为ttotal=LmaxN p tf[22]，其中，Np为种群中的个体数量且已在3.3.1 节给出。需要说明的是，在所关注的优化问题 P1和 P2中，决策变量维度分别为2M和M，而在进行环境适应度函数计算时，仍然把各节点的角度信息转换为二维坐标进行计算，因此所提算法与直接遗传算法的tfitness+tselection是近似相同的；由于tcrossover+tmutation和决策变量的维度有直接关系，因此所提算法的这部分时间成本更低。综上，在求解节点部署优化问题时，所提基于定位盲区预判断的遗传算法的时间复杂度比直接遗传算法稍具优势。

4 仿真验证与分析

本节通过计算机仿真，验证单信号源CRLB 的相关性质、验证与分析定位盲区的存在区域、对比不同传感器节点部署算法的性能。本节仿真所采用的仿真平台是安装于Intel(R) Core(TM) i9-9900K CPU @ 3.60 GHz 计算机的MATLAB R2021a 软件。

需要说明的是，针对单信号源CRLB 性质验证的主要目的是阐述测量误差给定时，定位几何构型对定位精度的影响；针对区域CRLB 性质验证的主要目的是给出定位盲区的出现区域，并说明与蒙特卡罗实验结果的一致性；针对传感器节点部署的仿真分析是为了说明所提算法的优势。

4.1 单信号源CRLB 性质验证

构建存在单信号源的二维定位场景，其中，信号源的位置坐标为u= [0,0]T，有M=5个传感器节点，位置坐标分别为s1= [300,100]T,s2=[400,150]T,s3= [300,500]T,s4= [350,200]T,s5=[ -100,-1 00]T。设这组传感器节点为 WSN1。在 WSN1的基础上，将传感器节点s1,s3,s5的位置坐标相对于信号源向外扩展，生成 WSN2={ks1,s2,ks3,s4,ks5}。在本节的仿真中，k=1.2。与 WSN2相比，WSN1传感器节点相对信号源的方向向量未发生变化，而部分传感器节点与信号源的距离变大了。

单信号源定位场景中Root CRLB 和均方根误差（RMSE,root mean squared error）的仿真结果如表1所示，其中，RMSE 是由200 次蒙特卡罗仿真得到的。CRLB 为均方误差（MSE）的理论下界，Root CRLB（即CRLB 的平方根值）为RMSE 的理论下界。由表1可知，当WSN中任一节点作为参考节点且TDoA测量误差协方差矩阵已知时，更换参考节点并不影响该WSN 对信号源的CRLB，RMSE 也近似相等。此外，当TDoA 测量误差的协方差矩阵不变且WSN 中部分传感器节点沿着信号源与传感器节点所在射线（需要保证方向向量不变）移动时，WSN 对信号源的CRLB 不变，RMSE 近似相等。

表1 单信号源定位场景中Root CRLB 和RMSE 的仿真结果

4.2 定位盲区仿真验证与分析

在对定位盲区的理论分析中，本文将CRLB 视为定位精度的衡量指标，因为CRLB 能够给出某一定位场景下WSN 对信号源定位精度的理论下界，即任何无偏估计定位算法的定位误差均大于CRLB。本节引入定位解析算法，并设置蒙特卡罗实验来计算定位解析算法的RMSE，通过与CRLB 进行对比分析来验证基于CRLB 对定位盲区分析的准确性。

考虑一个包含M=5个传感器节点的WSN，传感器节点呈线形排列，位置坐标分别为。WSN 的覆盖区域为正方形，即。将s1视为参考节点，设置TDoA 测量误差的标准差为。当给定WSN 中各个传感器节点的坐标后，对覆盖区域U均匀采样获取若干采样点，并计算每个采样点的CRLB，便可绘制覆盖区域内CRLB 分布等高线图。WSN 中节点线性排列时Root CRLB 和RMSE 的分布等高线图如图3 所示。需要说明的是，节点线性排列导致文献[4]算法产生奇异矩阵而失效。为了获取RMSE，本节利用一阶泰勒级数的方法[26]在真实信号源附近进行搜索。尽管如此，信号源真实位置作为初始点的泰勒展开法在绝对的定位盲点也无法获取信号源位置估计值。此外，在仿真图中，等高线所表示的定位精度单位为米，为避免文字重叠，图中将定位误差的单位省去，后续仿真图中等高线的定位精度单位也并未标注。

根据图3 可知，线形排列的WSN 所在直线为定位盲区，在该区域，CRLB 不存在，RMSE 无穷大。由WSN 所在直线的延长线两侧向WSN 所在直线的中垂线方向（[-5000,5 000]与[5 000,-5 000]连线的方向）移动，CRLB 逐渐变小，定位算法的RMSE 从“不存在”过渡为异常大。在中垂线方向，WSN 的定位精度最优，绝大多区域定位精度在10 m 以下。

为了论证定理1 中情况2 的定位盲区，将WSN中的s5由[ -2 500,-2 500]T移动至[ -2 500,-2 500]T，WSN 中节点的排列不再是线形，此时Root CRLB和RMSE 的分布等高线图如图4 所示。由图4 可知，1)s1至s4所在直线的外侧仍为定位盲区，CRLB 不存在，RMSE 无穷大；2) 偏出的节点s5附近并不存在定位盲区；3) WSN 节点所包围的区域内定位精度可达4 m，包围区域内不存在盲点。图4 的仿真结果与定理1 结论一致，结合图3 与图4 可证明推论1 的相关结论。

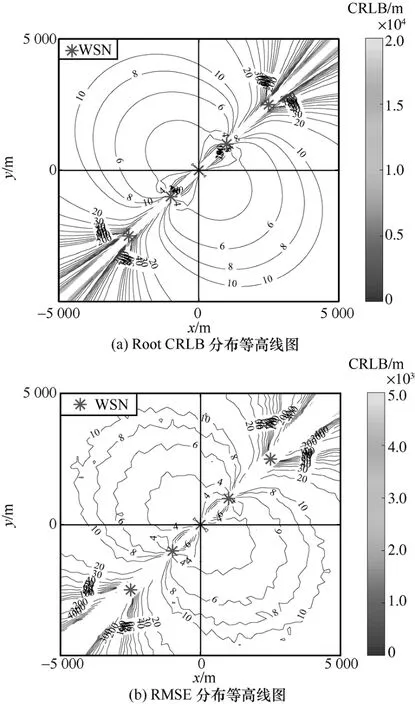
图3 WSN 中节点线性排列时Root CRLB 和RMSE 的分布等高线图

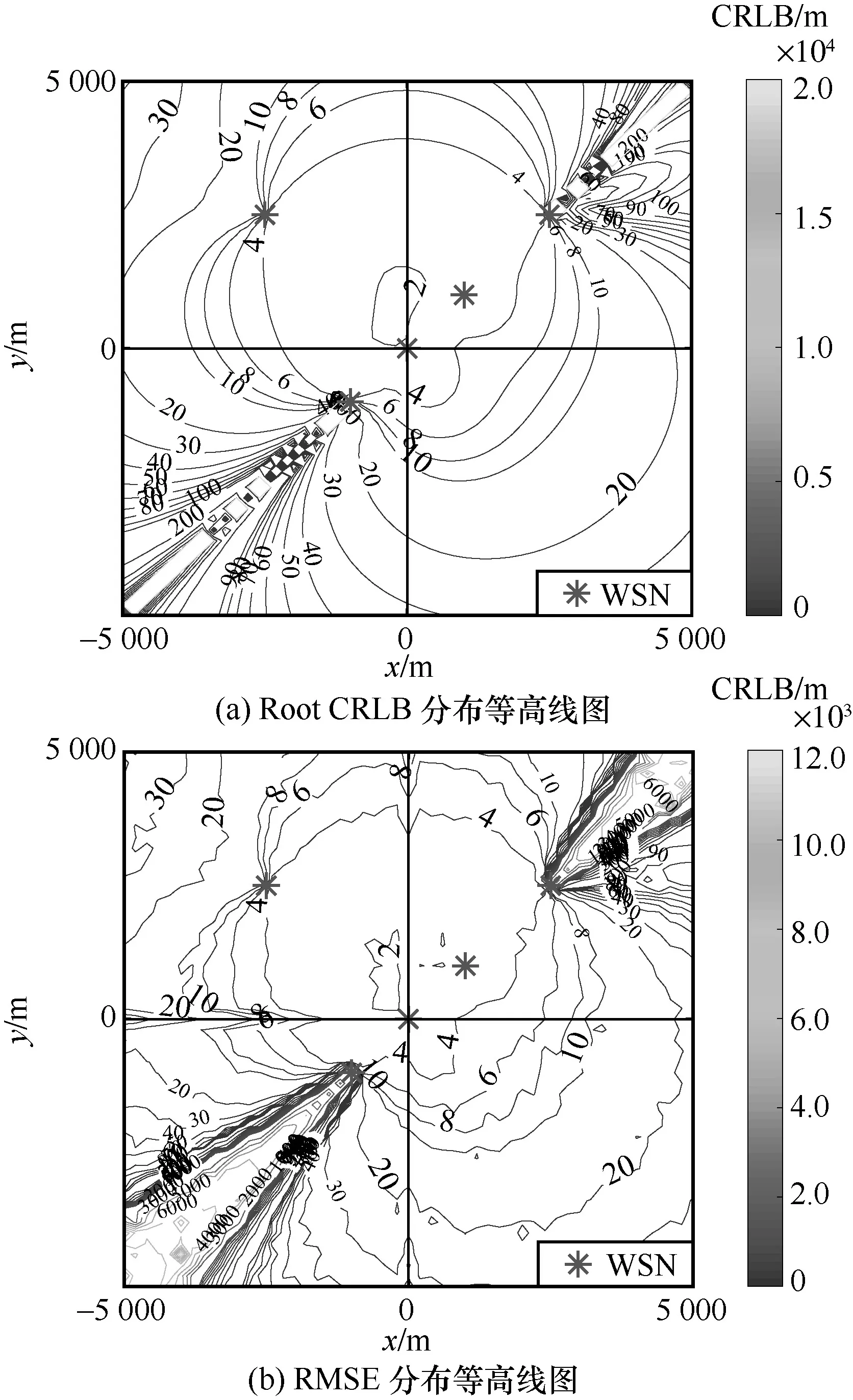
图4 WSN 中一个节点偏出时Root CRLB 和RMSE 的分布等高线图

进一步地，将WSN 中的s4由[ 2 500,2 500]T移动至[ 2 500,-2 500]T，此时WSN 相对于覆盖区域内任意一点的不同方向向量个数均大于2，不满足定理1中的情况2。WSN中2个节点偏出时Root CRLB和RMSE 的分布等高线图如图5 所示。由图5 可知，WSN 覆盖区域内不存在定位盲区，绝大多区域的定位精度在10 m 以下。图5 的仿真结果证明了定理1 的正确性。

图5 WSN 中2 个节点偏出时Root CRLB 和RMSE 的分布等高线图

为了验证推论2，本节选取图4 中的WSN 部署方式，并设置4 组不同的TDoA 测量误差标准差，即。TDoA 测量误差的标准差变化时Root CRLB 的分布等高线图如图6 所示。由图6 可知，TDoA 测量误差的强度并不影响CRLB的等高线分布，只是在不同的等高线上定位误差不同；当TDoA 测量误差为对角矩阵时，定位精度与测量误差的方差呈线性关系。需要说明的是，在研究无线定位网络空间几何构型的影响时，可将测量误差归一化，并采用定位精度几何因子（GDOP,geometric dilution of precision）作为分析对象[7]。

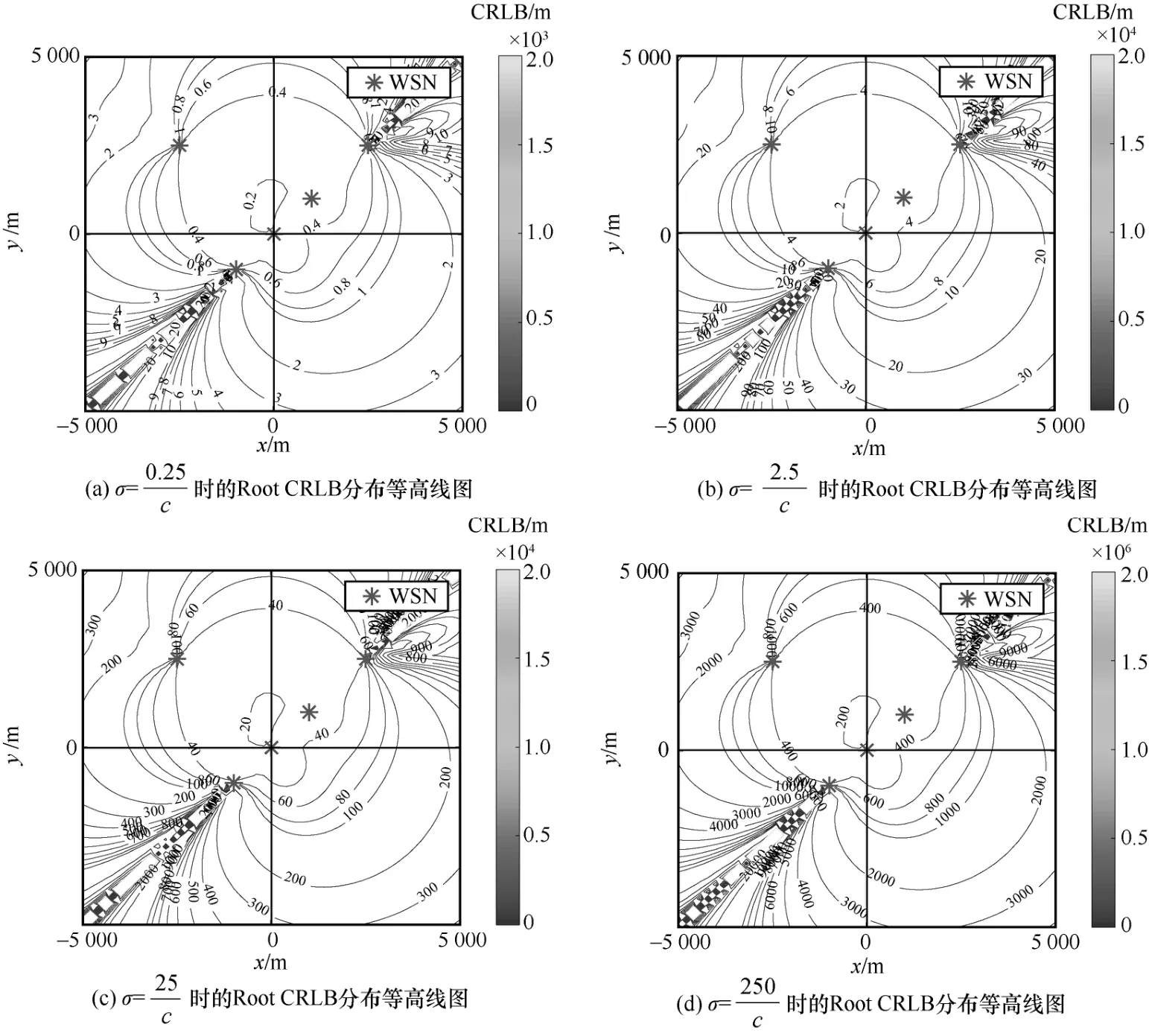
图6 TDoA 测量误差的标准差变化时Root CRLB 的分布等高线图

当WSN 仅保留3 个节点，且呈等边三角形式分布时，WSN 覆盖区域的Root CRLB 和RMSE 的分布等高线图如图7 所示。需要说明的是，三节点TDoA 定位场景的RMSE 是利用文献[27]中所提出的算法，结合一阶泰勒展开法获得的。由图7 可知，在任意2 个节点的外侧，存在定位盲区，不存在CRLB，RMSE 无穷大；在节点包围区域的内部，不存在定位盲点，这与推论3 是一致的。

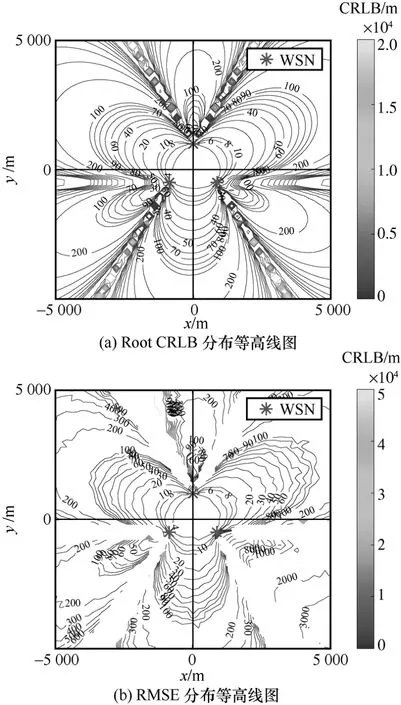
图7 WSN 仅包含3 个节点时Root CRLB 和RMSE 的分布等高线图

4.3 传感器节点部署算法验证与分析

由图3～图5 可知，当传感器节点部署方式发生变化时，覆盖区域内定位精度的等高线也在发生变化。本节通过仿真分析的形式，研究覆盖区域平均CRLB 最小化的传感器节点部署算法。

考虑存在M=5个节点的WSN，假设其部署区域与覆盖区域相同，即S==[ -5 000,-5 000]T×[ 5 000,5 000]T。假设不考虑传感器节点的通信距离与覆盖范围约束，并设置TDoA 测量误差的标准差为。

为了验证所提的基于定位盲区预判断的遗传算法，本节设计了3 个对比算法：均匀角度部署算法、区域顶点部署算法、直接遗传算法。均匀角度部署算法以覆盖区域为中心，将全部传感器节点部署于。区域顶点部署算法将4 个传感器节点部署于覆盖区域的4 个顶点，另外一个位于覆盖区域的中心。直接遗传算法如3.3.1 节所述，将传感器节点的空间位置作为决策变量，在覆盖区域S中迭代搜寻，获取使平均CRLB 最小的节点部署方案。

4 种节点部署算法对覆盖区域定位的性能对比如图8 所示。由图8(a)可知，所提基于定位盲区预判断的遗传算法能够获得最小的平均Root CRLB，对应的节点部署方案能实现覆盖区域内信号源的最优定位精度。当 TDoA 测量误差的方差为时，所提算法对于区域的平均定位精度比均匀角度部署算法提高了33.92%，比区域顶点部署算法提高了13.74%，比直接遗传算法提高了9.65%。

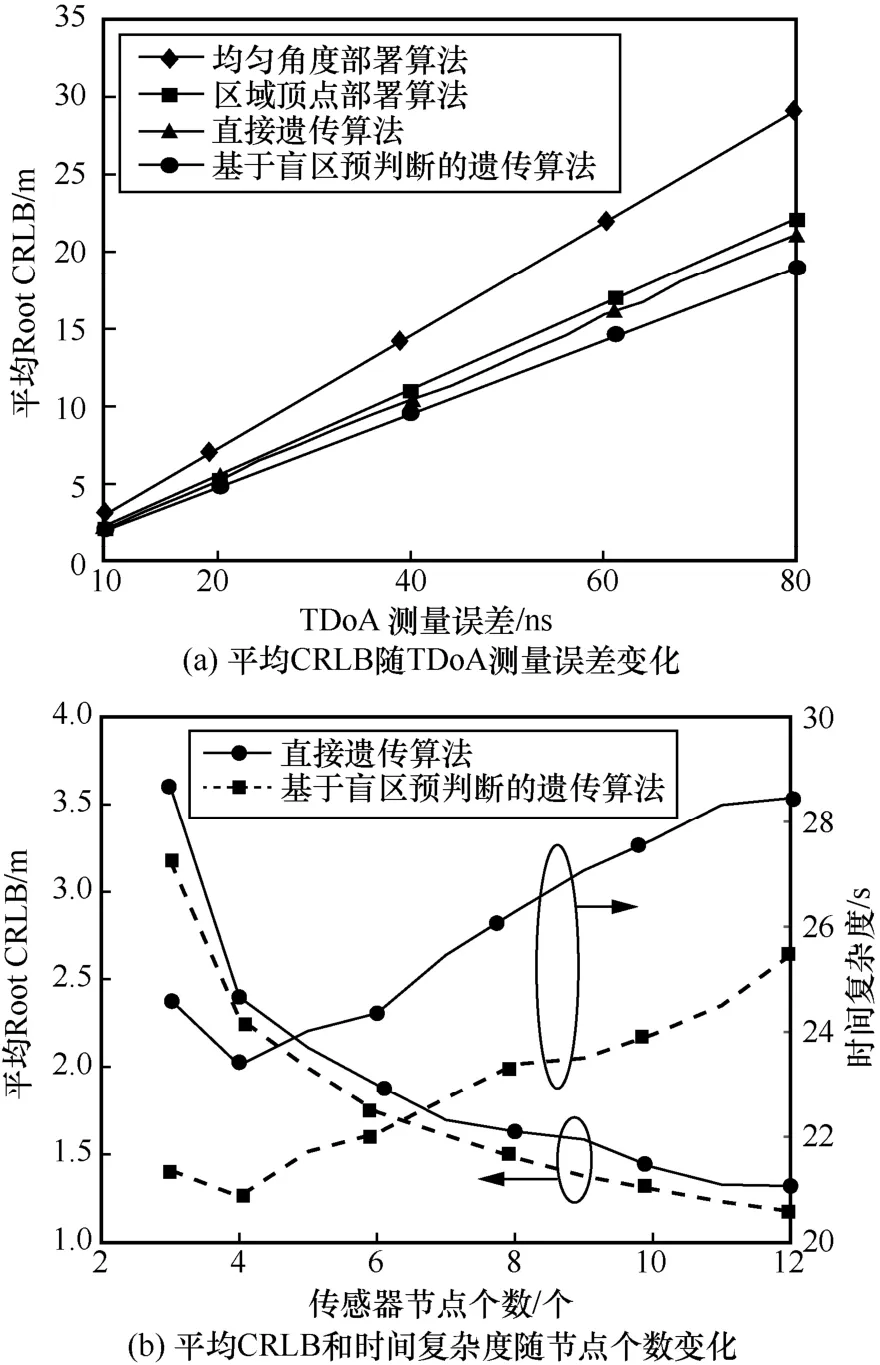
图8 4 种节点部署算法对覆盖区域定位的性能对比

图8(b)中时间复杂度由算法的运行时间反映。直接遗传算法和所提基于定位盲区预判断的遗传算法中均设置种群规模为100，最大迭代次数为200 次，算法终止条件为目标的迭代增量。由图8(b)可知，随着可部署的传感器节点个数的增加，2 种算法可获得的平均Root CRLB 都在逐渐变小，这表示部署更多的传感器节点可提升覆盖区域内目标的定位精度。其次，基于定位盲区预判断的遗传算法运算时间小于直接遗传算法，这是因为直接遗传算法在定义域内进行全域搜索，且决策变量维度较高，而所提算法只在部署区域的边界进行迭代搜索，且决策变量维度较低，因而时间复杂度也较低。

图9 典型TDoA 测量误差下4 种节点部署算法对区域定位时平均Root CRLB 分布等高线图

5 结束语

本文针对TDoA 为定位参数的WSN，从单信号源定位精度CRLB 入手，探讨了传感器节点与信号源的方向向量对CRLB 的影响，给出了定位盲区产生的充分条件，并分析了TDoA 测量误差、传感器节点排列方式等多种因素对定位盲区的影响。在此基础上，构建了传感器节点部署问题，并提出了基于定位盲区预判断的遗传算法来求解。仿真表明，所提算法相较于区域顶点部署、均匀角度部署、直接遗传算法，可将定位精度大幅提升。本文提出的定位盲区研究方法对已部署网络的定位性能分析具有参考意义，所提节点部署方案对待部署网络的定位盲区出现区域具有指导意义，具有广泛的应用前景。