基于时空和作战编组的兵棋推演系统轨迹聚类算法
2023-02-19万宜春陈志龙何昌其
万宜春,陈志龙,何昌其,胡 水
(陆军指挥学院,江苏 南京 210045)
兵棋推演系统是在虚拟环境中检验作战计划的重要手段,主要组成为棋盘、棋子和裁决规则[1]。推演人员在兵棋推演系统上对棋子下达的各种指令,都会按照裁决规则计算结果转化为机动、直瞄、间瞄、飞行、侦察等相应行动及棋盘态势。随着推演进程的发展,棋子的位置也在不断发生变化。为提供推演后的复盘回放和数据分析功能,兵棋系统需记录下推演过程中所有棋子的位置信息,形成大量轨迹数据。这些轨迹数据除了位置信息,还记录了途经时间以及关联棋子的基本信息。在战术及以上级别的兵棋推演中,轨迹数据存在机动形态杂,数据存储大和轨迹不连续等问题。另外,轨迹数据在时间维度、空间维度和棋子维度上涉及范围广,加上停留点和细微机动调整点的存在,使得兵棋轨迹数据更加复杂。传统兵棋系统往往缺乏对轨迹数据的处理手段,直接将其呈现在兵棋系统上,不便于指挥员快速理解作战态势,给复盘分析、组织协同和方案评估等工作带来较大困难[2]。为此,有必要研究轨迹聚类方法,从繁杂的轨迹信息中提取主要内容,使其既能简洁概述兵棋推演的整体态势变化,又不丢失棋子机动过程中的重要细节信息。
本文回顾了轨迹聚类的相关工作,设计了CTUW算法,通过实验测试了CTUW算法的运行效果,验证了其用于兵棋推演系统轨迹聚类的可行性。
1 轨迹聚类的相关研究
轨迹聚类可被视为一种数据处理框架,涉及轨迹压缩、相似性度量、聚类和可视化等4个步骤,前3项内容是轨迹聚类的中心工作[3]。
轨迹压缩主要完成去除冗余点和提取关键点的工作,在不丢失轨迹关键特征信息的前提下,尽可能压缩轨迹存储信息。李名[4]等引入了经典的Douglas-Peucker算法[5]用于查找停留点等冗余信息,以达到压缩轨迹信息的目的。Li Q[6]等提出基于几何特性的停留点检测方法,算法简单高效,但需要根据不同样本调整参数。徐凯[7]等将时间维纳入考虑依据,将轨迹压缩算法转换到向量空间执行,进一步改善了压缩效率。董婉婷[8]等基于Sliding Window算法[9],在删除停留点的同时,尽可能保留轨迹特征点,丰富了压缩轨迹的局部形态特征。
相似性度量用于对轨迹之间相似性进行评估量化,是聚类算法的前提和数据基础。常用的相似性度量方法包括欧氏距离、隐马尔科夫模型、最长公共序列和动态时间调整等。Lee[10]等从垂直距离、平行距离和角度聚类3个层面量化空间维度上的相似度,该方法不受轨迹线段长短的限制,较好地度量了轨迹线段之间的空间相似度。郭名静[11]和龙真真[12]等利用多维属性对聚类划分的共同影响,从非地理空间的数据维度入手,设置了不同数据维度对空间距离的影响权值,以修正相似性度量函数。周超[13]等结合军事运用的需求,构建了基于实体、行动和交互等要素的兵力聚合模型,使用层次分析法确定权重影响矩阵,并依此计算相似度。
聚类算法是轨迹聚类的核心,目的是将相似轨迹聚合为类簇[14]。典型的聚类算法包括基于划分的K-means算法、基于层次的CHAMELEON算法、基于网络的CLIQUE算法、基于图论的Spectral Clustering算法、基于密度的DBSCAN算法和DPC算法等,它们被广泛应用于模式识别、机器学习和数据挖掘等领域。兵棋推演系统的轨迹信息属于分布形态随机性大、类簇重叠频率高的数据样本,大多数传统聚类算法处理这类数据样本的效果均不佳[15]。然而,DBSCAN[16]和DPC[17]等基于密度的聚类算法能够适应非球形分布的数据样本。DBSCAN算法提出的密度可达概念,可以在嘈杂的样本中找到形状各异的类簇,但是该算法的输入参数设定缺乏理论支撑,参数值受主观影响较大,且在处理密度重叠样本方面存在短板。DPC算法,又称为密度峰值聚类算法,除能够解决非球形聚类问题外,还更容易确定唯一的输入参数,在处理类簇重叠的数据样本时,也能保持较好的聚类效果,因此近年来受到广泛关注[15]。
本文的轨迹聚类基本思路是先分割后聚合,与该思路比较接近的有TRACLUS算法[10]和CTECW算法[3],但是这些算法存在以下不足。
1)在轨迹压缩方面,TRACLUS算法采用MDL(最小描述长度)方法进行轨迹压缩,压缩效果不佳,且计算较复杂[18]。CTECW算法引入了简化轨迹概念,先将原始轨迹转化为简化轨迹,再进行分段,进一步优化了轨迹分段效率,但还是无法查找停留点,轨迹压缩率有待进一步提高。
2)在相似性度量方面,TRACLUS算法和CTECW算法仅从空间维度上定义了相似度,只能根据空间距离相邻关系对轨迹进行聚类。若直接将这两个算法应于兵棋推演系统,其无法利用轨迹的时间和棋子编组关系等信息进行精细化轨迹聚类,导致静态图形式的聚类结果无法反映不同作战时节、不同作战力量、不同类型行动的动态机动情况,影响了轨迹聚类的军事应用意义。
3)在轨迹线段聚类方面,TRACLUS算法和CTECW算法均是基于DBSCAN聚类算法的基本框架。受到DBSCAN算法短板的影响,这两个算法无法适应类簇交叉重叠的数据样本,且DBSCAN算法的输入参数较多,参数值受主观影响波动较大。虽然CTECW算法使用密度估计熵为参数值的选择提供了重要理论依据,但实质上变相增加了数据预处理的环节,降低了算法应用的灵活性。
4)在可视化方面,TRACLUS算法为每个轨迹线段类簇提取代表轨迹后,没有进一步处理,导致代表轨迹线段较为凌乱,可读性不高。CTECW算法通过分析代表轨迹之间的后继关系,试图进一步提升轨迹聚类效果,但是其使用的后继关系分析方法容易出现“后继循环”,反而可能造成轨迹聚类结果的错误表达。
针对以上不足,本文提出CTUW算法:首先,对原始轨迹进行压缩,去除停留点等冗余信息,提取轨迹特征点并进行轨迹分段;再基于提出的时间、空间和编组关系相似度计算方法,定量描述轨迹线段之间的相似性;然后,使用DPC聚类算法对轨迹线段进行聚类;最后,根据兵棋推演系统轨迹聚类的军事需求,可视化展示聚类结果。
2 CTUW算法
2.1 轨迹压缩
定义1棋子轨迹:每个棋子在推演过程中都会产生一条轨迹记录。从棋子轨迹起点开始,兵棋系统每间隔一段时间采集棋子位置信息,这些信息按照采集时间由先到后的顺序排列得到的序列即为棋子轨迹。用Tra表示棋子轨迹:
Tra=p1p2…pkpk+1…pn
(1)
其中,pk=(xk,yk,tk),xk为棋子位置的横坐标,yk为棋子位置的纵坐标,tk为棋子途径位置时的作战时间。
定义2特征点:在轨迹中,棋子的运动趋势发生较大改变的点称为特征点。特征点集合用F表示。
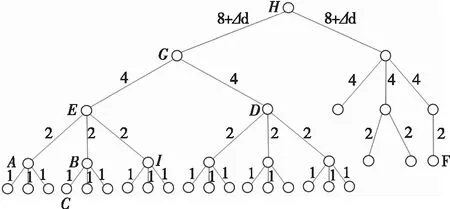
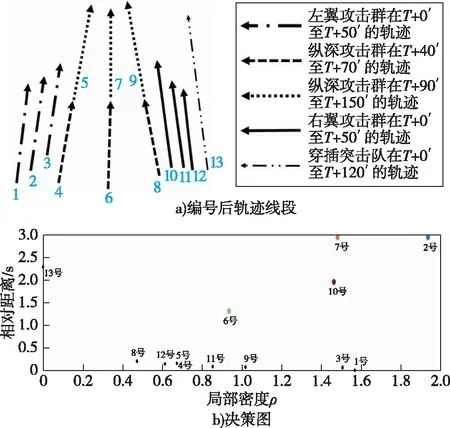
定义3停留点:在轨迹中,若某时刻记录的棋子位置点相比前一时刻没有发生明显的位置变化,则称为停留点,用si(1 图1 停留点示意图 定义4轨迹线段:选取轨迹中的pi点和pj点(i 定义5轨迹段:选取轨迹中的多个点{pk1,pk2,…,pkm}(k1 T={pk1pk2,pk2pk3,…,pkipki+1,…,pkm-1pkm} (2) 按照定义5,棋子的原始轨迹可以写成轨迹段形式,表示为 Toriginal={p1p2,p2p3,…,pipi+1,…,pn-1pn} (3) 兵棋系统为了记录推演过程,将每隔一段时间记录一次棋子的位置和采集时间,由此构成棋子的轨迹信息。轨迹中有一些冗余信息,不仅对轨迹聚类的最终效果没有贡献,反而会增加轨迹聚类算法的时间和空间复杂度。冗余信息主要分为两类:一类是非特征点带来的冗余信息,即棋子运动趋势基本保持不变的一段轨迹上的若干个连续轨迹信息,如图2所示,非特征点p2参与的轨迹段{p1p2,p2p3}描述的是略微曲折的一小段轨迹,而这种信息对反映棋子整体机动意图的作用不大。如果将其简化为轨迹段{p1p3},不仅不会影响轨迹信息的概述,还将降低轨迹聚类算法的空间和时间复杂度,甚至还能避免轨迹聚类算法出现过度拟合。另一类冗余信息是停留点带来的冗余信息,即处于停留状态的一段轨迹上的若干个连续轨迹信息,如图2所示,轨迹段{p3p4,p4p5}和轨迹段{p7p8,p8p9,p9p10}都处于停留状态,它们无须被轨迹聚类,因此可以将其删除。 图2 轨迹压缩示意图 定义6轨迹压缩:从原始轨迹删除停留点和非特征点带来的冗余信息后,形成多个新的轨迹段,这些轨迹段组成的集合称为压缩后的轨迹,用Tcompress表示。 如图2所示,棋子原始轨迹Tra对应的轨迹段为{pipi+1|1≤i≤10},经过轨迹压缩后,得到轨迹段集合: Tcompress={{p1p3},{p5p6,p6p7},{p10p11}} 压缩前原始轨迹共有10个轨迹线段,压缩后仅为4个轨迹线段,说明轨迹信息确实被压缩。另外,原始轨迹为1个轨迹段,压缩后被切分化为3个轨迹段。这种轨迹压缩方法虽然把连续轨迹转化为不连续的多个轨迹段,但本文的CTUW算法基本思路是先分割后聚合,轨迹压缩环节要为后续的聚类算法提供的本来就是分割后的轨迹线段,且轨迹间断的位置对应的是对轨迹聚类没有帮助的停留点信息,所以,压缩后轨迹可能不连续的结果不会对轨迹聚类造成不良影响。 如图3所示,轨迹压缩分为3个阶段:查找原始轨迹停留点,将原始轨迹切割为多个轨迹段,查找每个轨迹段特征点。 图3 轨迹压缩流程示意图 设原始轨迹点数量为n,算法具体步骤如下: 1)i=2; 2)若i大于n,则跳转到第7)步; 3)从pi-1点开始,向轨迹起点方向遍历,寻找首次满足以下条件的pj点:pj点与pi点的时间距离大于等于时间阈值timeThreh,且pj+1点与pi点的时间距离小于时间阈值timeThreh。若无法找到这样的pj点,则i=i+1,且跳转到第2)步; 4)若pj点与pi点的空间距离小于距离阈值distThreh,则从pj点开始,沿原始轨迹Tra向轨迹起点方向遍历,寻找首次满足以下条件的pk点:pk-1点与pj点的空间距离大于等于距离阈值distThreh,且pk点与pj点的空间距离小于距离阈值distThreh。若遍历到p1点时,都没有找到满足该组合条件的pk点,则令k=1; 5)点集合{ph|k+1≤h≤i}中所有点均为停留点; 6)i=i+1,且跳转至第2步; 7)按照以下规则,初步设置轨迹上的特征点:①若ph点为停留点且ph+1点为非停留点,则ph点也是特征点;②若ph点为非停留点且ph+1点为停留点,则ph点是特征点;③p1点为特征点;④若pn非停留点,则为特征点; 8)从原始轨迹Tra中删除那些不是特征点的停留点,则原始轨迹被切割为若干个轨迹段T1、T2、…、Tm。根据第7)步的原则,这些轨迹段的起点和终点肯定为特征点; 9)针对T1、T2、…、Tm中的每个轨迹段,都进行以下步骤寻找轨迹段内的特征点,将找到的特征点连线成为压缩后的轨迹段; 10)假设某个轨迹段起点的序号为s,终点的序号为e,则该轨迹段对应的轨迹为psps+1…pe; 11)设置该轨迹上的滑动窗口{pipi+1…pj},其中s≤i≤j≤e,初始化该窗口为i=s,j=i+1; 12)针对滑动窗口内pi+1点、pi+2点、…、pj点,逐个计算每个点到线段pipj的欧氏距离; 13)若这j-i个欧氏距离均小于距离阈值feaThreh,则j=j+1,且跳转到第12)步。否则,pj-1点为特征点,i=j-1,且跳转到第12)步。 以上算法中,步骤1)~6)为查找原始轨迹停留点的阶段,步骤7)~8)为将原始轨迹切割为多个轨迹段的阶段,步骤9)~13)为每个轨迹段查找特征点的阶段。其中,timeThreh和distThreh的含义是棋子途径某个点之后timeThreh时间,棋子仍在该点附近distThreh距离范围内,则认为棋子处于停留状态。 轨迹压缩算法的步骤第9)~13),采用Sliding Window算法查找特征点,该算法擅长局部轨迹的压缩优化。兵棋棋子轨迹压缩,需要体现关键路口、特殊地貌和限制地物等通行环境对机动路线规划的影响,还需要体现穿插、迂回和渗透等行动的特点,所以,兵棋轨迹压缩需要在删除冗余信息的同时,保留更多局部特征点,Sliding Window算法较好满足了该需要。该算法的基本思想是使用滑动窗口向后遍历轨迹,每次以刚找到的最新特征点为滑动窗口的起点向后探索,找到下一个特征点作为滑动窗口的终点,下一特征点还应满足以下两个条件:滑动窗口起点和终点组成连线,窗口内所有点到该连线的欧氏距离小于设定的距离阈值;在固定滑动窗口起点的前提下,尽可能使窗口范围更大。如图4所示,设原始轨迹起点p1为特征点,初始化滑动窗口为{p1p2}。滑动窗口{p1p2}内的两个点到线段p1p2的距离小于设定的距离阈值feaThreh。进一步扩大滑动窗口范围,将滑动窗口的终点后移一位,扩展为窗口{p1p2p3},该窗口内所有点到线段p1p3的欧氏距离均小于设定的距离阈值feaThreh。尝试进一步扩大滑动窗口为{p1p2p3p4},在该窗口内p3点到线段p1p4的欧氏距离大于设定的距离阈值feaThreh,说明{p1p2p3}是固定滑动窗口起点p1的前提下能够找到的符合搜索条件的宽度最大的滑动窗口。滑动窗口{p1p2p3}的终点p3为轨迹上特征点p1之后的下一个特征点。接着以p3点作为新的滑动窗口的起点,将滑动窗口设定为{p3p4},重复以上步骤。在滑动窗口{p3p4}逐步扩展到{p3p4p5p6}的过程中,发现滑动窗口内所有点到滑动窗口起点与终点连线的欧氏距离始终小于设定的距离阈值feaThreh。因此,滑动窗口{p3p4p5p6}的终点p6也为特征点。最终,图4中轨迹特征点为p1、p3和p6点。 图4 轨迹压缩流程示意图 轨迹聚类是对多个棋子在一段时间内产生的众多轨迹线段进行聚类,聚类的前提是能够准确描述轨迹线段两两之间的相似性。相似性度量的具体方法直接体现了轨迹聚类的意图,影响轨迹聚类的效果。石崇林等针对兵棋系统提出轨迹聚类算法CTECW,巧妙设计了轨迹线段之间的空间距离计算方法,能够满足对称性、非负性和三角不等式关系。但是,CTECW算法忽视了兵棋轨迹是复合了时间、空间和关联棋子信息的组合体,不能单纯将地理位置相近的多个轨迹聚合在一起,而应将时间、空间和关联棋子的编组关系都相近的多个轨迹聚合在一起。只有这样,轨迹聚类的最终结果才不是一个静态的线段组合图,而是一个能够反映时空动态变化的多群队机动态势图。 如图5a)所示,10个棋子分为左翼攻击群、纵深攻击群、右翼攻击群和穿插突击队等4个群队,产生了多条轨迹,图例说明了每条轨迹的发生时间以及隶属群队名称。 如图5b)所示,传统轨迹聚类算法TRACLUS的聚类效果仅能反映全局棋子的运动趋势,因为其只将轨迹线段之间的空间距离作为相似性度量依据,所以聚类效果不精细。 如图5c)所示,CTECW算法相比TRACLUS算法,优化了相似性度量方法和轨迹线段聚类算法,聚类结果反映了更多的细节信息。但是CTECW算法还是仅从空间距离这单一层面优化了相似性度量方法,导致聚类类簇内部各轨迹线段在群队关系和时间方面不具备相似性,不易理解聚类结果。图5c)左侧的轨迹线段类簇中,包含了两个群队的轨迹,而且原本应分为3个时间段(T+0′至T+50′、T+40′至T+70′、T+90′至T+150′)的轨迹被合并到了该类簇中。图5c)右侧的轨迹线段类簇,包含了3个群队的轨迹,原本应分为4个时间段(T+0′至T+50′、T+40′至T+70′、T+90′至T+150′、T+0′至T+120′)的轨迹被合并到了该类簇中。使用CTECW得到的类簇内部,轨迹线段的编组关系和时间分布较为凌乱且缺乏规律,难以清晰体现轨迹聚类后的军事含义,影响了该算法的军事应用价值。 如图5d)所示,本文提出的CTUW算法从时间、空间和编组关系等3个维度进行轨迹线段的相似性度量。因此,不仅能够将相邻的多个群队轨迹分离开,还能对纵深攻击群各作战时节机动轨迹进一步分割,最终将4个群队10个棋子的13条轨迹线段聚类成5个类簇,每个类簇内部的轨迹在时间、空间和编组关系上均具相似性。按照该相似性度量的思路,能使聚类结果既细致体现多群队机动轨迹的时空变化规律,又便于精炼概括各个聚类类簇的军事含义。 图5 轨迹聚类效果对比图 2.2.1 空间相似度 CTECW算法能够较为全面地计算两个轨迹线段之间的空间距离。本文在此基础上,改进了部分计算公式,并就相关权值的选取给出了分析。 定义7空间平移距离:轨迹线段Li与Lj之间的空间平移距离,指线段Li中点与线段Lj中点连线的线段长度,用geoShiftDistij表示。 定义8空间角度距离:轨迹线段Li与Lj之间的空间角度距离,指平移线段Li使其中点与线段Lj中点重合后,线段Li终点与线段Lj终点连线的线段长度,即 geoAngleDistij= (4) 其中,θij为线段Li与线段Lj之间的夹角,且满足0≤θij≤π。 定义9空间距离:轨迹线段Li与Lj之间的空间距离由空间平移距离和空间角度距离组成,即 geoDist(Li,Lj)=ωgeoShift·geoShiftDistij+ωgeoAngle·geoAngleDistij (5) 其中,权重ωgeoShift和ωgeoAngle的取值依据不同聚类需求。geoShiftDistij反映两个轨迹线段质心间的距离,geoAngleDistij反映两个轨迹线段的向量夹角大小和线段长度差异。相关权重的默认取值为:ωgeoShift=1,ωgeoAngle=1。根据不同应用场景,还可以调整权重值:若轨迹线段聚类侧重运动方向相似、线段长度相似等因素,那么,可以适当增加ωgeoAngle的取值;若仅侧重考虑轨迹线段间隔距离,则可适当增加ωgeoShift的取值。另外需要说明的是,在CTUW算法执行聚类前,会对时间、空间和编组关系这3个相似度值进行归一化处理,所以调整权重ωgeoShift和ωgeoAngle取值的主要目的是调整权重的相对比值,而不是权重的绝对大小。 2.2.2 时间相似度 在兵棋推演过程中,常常出现两个棋子先后通过同一路段的情况。例如,棋子A在t1时刻途经1号点,沿着某公路机动,在t2时刻到达2号点;棋子B在t1+Δt时刻途经1号点,沿着同一公路机动,在t2+Δt时刻到达2号点。两个棋子的轨迹线段起始时间差为Δt,终点时间差也为Δt。若按照“起始时间差+终点时间差”的方式计算时间距离的话,将得到2·Δt,这会过度放大两个轨迹线段之间的时间相似度,影响轨迹聚类效果。相比之下,两个轨迹线段的时间距离取值Δt可能更合适。为此,本文取起始时间差和终点时间差的最大值作为时间相似度。 假设轨迹线段Li=psipei,psi点是Li的起点,pei点是Li的终点,途径psi点的时刻为tsi,途径pej点的时刻为tei,则轨迹线段Li的发生时间段为tsi至tei。同理,轨迹线段Lj的发生时间段为tsj至tej。两个线段的起始时间差为|tsi-tsj|,终点时间差为|tei-tej|。 定义10时间距离:轨迹线段Li与Lj之间的时间距离为 timeDist(Li,Lj)=max(|tsi-tsj|,|tei-tej|) (6) 其中,函数max(x,y)表示取x与y中的最大值。 2.2.3 编组关系相似度 轨迹线段Li与Lj编组关系相似度主要用于描述Li关联棋子与Lj关联棋子之间的编组关系亲疏程度,作为相似性度量的组成部分,引导聚类算法尽可能将同一群队的轨迹聚为一类。 在实际作战和兵棋推演中,参战单位是以作战编组的结构进行组织的,而且作战编组结构是作战和推演前的已知信息,基于该信息即可知晓每个作战实体或棋子隶属于哪个群队。如图6所示,作战编组可用树状结构表示。一般情况下,兵棋系统的各个棋子为树状结构中的叶子节点。为提升算法普适性,本文假设该结构的非叶子节点也能对应兵棋棋子。 图6 编组关系树状结构图 兵棋系统中,两个棋子的编组关系相似性就是它们在作战编组结构中的关系远近程度。根据作战编组含义,为满足轨迹聚类需求,编组关系相似性度量算法应满足以下几个性质:1)低层级的兄弟棋子之间编组关系比高层级的兄弟棋子之间编组关系紧密;2)父子棋子的编组关系比兄弟棋子紧密;3)兄弟棋子之间编组关系比叔侄棋子紧密;4)隔代少的近亲棋子之间编组关系比隔代多的紧密;5)共同祖先层级低的棋子之间编组关系比共同祖先层级高的紧密;6)同一棋子的两个轨迹线段编组关系距离为0。 定义11编组关系距离:轨迹线段Li与Lj之间的编组关系距离,也是它们关联棋子Ci和Cj的编组关系距离,即棋子在编组关系树状结构图中的最短路径的长度,表示为orgaDist(Li,Lj)或者orgaDist(Ci,Cj)。其中,树状结构中每条边的长度值按照如下规则设置:最低层级的边长为1,上一层级的边长是下一层级的2倍,最顶部边的边长在此计算模式基础上额外增加特定正数Δd,Δd的取值根据具体应用场景而定。 结合图6示例,检验定义11是否满足编组关系相似度应具备的几个性质:低层级的兄弟棋子orgaDist(A,B)为4,高层级的兄弟棋子orgaDist(D,E)为8,满足性质1);父子棋子orgaDist(E,A)为2,兄弟棋子orgaDist(A,B)为4,满足性质2);兄弟棋子orgaDist(A,B)为4,叔侄棋子orgaDist(A,C)为5,叔侄棋子orgaDist(D,A)为10,满足性质3);隔1代的近亲棋子orgaDist(D,A)为10,隔2代的近亲棋子orgaDist(D,C)为11,满足性质4);H比G的层级高,共同祖先为G的棋子orgaDist(D,A)为10,共同祖先为H的棋子orgaDist(A,F)为28+2·Δd,满足性质5);结合定义11,易证其满足性质6)。 2.2.4 轨迹线段相似度距离 定义12轨迹线段相似度距离:轨迹线段Li与Lj之间的相似度距离表示为 Dist(Li,Lj)=ωgeo·geoDist′(Li,Lj)+ωtime·timeDist′(Li,Lj)+ωorga·orgaDist′(Li,Lj) (7) 其中geoDist′、timeDist′和orgaDist′为归一化后的数值。默认情况下,权重ωorga取值为1。因为同一编组内棋子的轨迹相对集中,编组关系距离与空间距离具有强相关性,为避免重复放大差异,权重ωgeo取值应小于1。当仅需要考虑全时段机动轨迹整体趋势时,权重ωtime可以小于1,甚至取值为0。当需要详细展示不同作战时节机动轨迹聚类情况时,权重ωtime应该大于等于1。 Dist(Li,Lj)的取值越小,轨迹线段Li与Lj之间相似度越高。 兵棋推演系统轨迹线段的聚类具有以下几个特点:1)每场兵棋推演可能都不一样,轨迹聚类前无法向聚类算法提供先验知识;2)与决心图的进攻方向标绘方式类似,轨迹线段非球形分布,通常呈曲线分布形态;3)群队之间可能在时间和空间上存在轨迹的重叠或交叉;4)高速机动棋子(如飞机)或者特殊作战节奏的棋子(如战斗预备队)轨迹在聚类过程中,常以噪声的形式存在,不适合与其他轨迹有效聚合,需要查找到这类特殊轨迹并在聚类结果中单独呈现,以突出诸军兵种机动方式的多样性。 DPC聚类算法能较好适应该应用场景,因为该算法无需先验知识就可以处理非球形分布的数据,在处理类簇重叠的数据方面有较好的聚类效果,并且具有较强的噪声处理能力。本文采用DPC算法的框架来进行轨迹线段的聚类。 设D是压缩轨迹Tcompress内所有轨迹线段的集合,表示为D={L1,L2,…,Lm}。 定义13局部密度:轨迹线段Li的局部密度为 (8) 其中,dc为截止距离,是DPC算法需要人工设定的唯一参数。默认情况下dc的取值达到如下情况时为佳:将所有轨迹线段之间的相似度距离按照由小到大的顺序排序,dc是该序列前1%至2%位置处的值。根据轨迹聚类的不同需求,还可进一步调整dc取值:当需要进一步详细切分不同作战时节、不同作战地域、不同作战编组的轨迹聚类效果时,可适当减小dc取值;当需要从全局、全程、全时的更高视角通盘掌握棋子轨迹态势时,可适当增加dc取值。 定义14相对距离:轨迹线段Li的相对距离指局部密度大于ρi的轨迹线段中离Li最近的相似度距离。但当轨迹线段Li的局部密度最大时,该线段的相对距离取值为所有轨迹线段相对距离的最大值。定义为 (9) 按照以上定义,可以得到每个轨迹线段的局部密度和相对距离,将其绘制在决策图上,如图7所示。对图7a)中各个轨迹线段进行编号,然后,基于轨迹线段之间的相似度距离使用DPC算法聚类,得到的决策图7b)。 图7 编号后的轨迹线段与决策图对应关系 选取决策图中局部密度ρi和相对距离δi都较大的轨迹线段作为类簇中心。如图7b)所示,选取了2、6、7、10号轨迹线段作为类簇中心。 再将其他非类簇中心的各个轨迹线段划分到距离其最近的更高局部密度轨迹线段所属类簇中,即可完成轨迹线段的初步聚类。如图8所示,依据已经确定为类簇中心的4个轨迹线段,其他非类簇中心的轨迹线段也将归类到距离其较近的类簇中,例如,在比3号轨迹线段局部密度大的所有轨迹线段中,2号是离3号最近的轨迹线段,因此,3号轨迹线段应与2号归为一类,依此方法,即可将13条轨迹线段初步划分为4个类簇。 图8 轨迹线段初步聚类效果图 为了更好地说明聚类效果,我们将本文中提出的时间、空间和编组关系这3个维度的距离压缩为2个维度,如图9所示,横坐标为时间距离和空间距离的复合表达,纵坐标为编组关系距离,图9中的编号与如图7b)对应。结合图7b)的颜色示例,图9还说明了初步聚类的结果,例如图9左下角的3个蓝色样本点及其附近文字说明了1、2和3号轨迹线段同属于以2号轨迹线段为中心的类簇。 图9 轨迹线段相似度距离的二维视角图 图9中,10、11、12和13号都是棕色,图7b)中10号也是棕色,说明图7a)中的10、11、12和13号轨迹线段被初步聚类归为一个类簇。但是从图7a)上可以看出,13号轨迹线段与其他轨迹线段在时间、空间和编组关系方面都存在较大差异。在图9中,13号距离其所归属类簇的中心10号的时空距离和编组关系距离均较远,13号实际上应为离群轨迹线段。那么,13号被归入以10号为中心的类簇的原因是,众多类簇其实都远离13号,以10号为中心的类簇只是这些类簇中离13号相对近一点的类簇而已。因此,13号这种离群轨迹线段,不应被划分到任何类簇,而应在轨迹聚类最终结果中单独显示。为了分离出该类离群轨迹线段,我们进行如下定义。 定义15外围区域:若轨迹线段Li属于某个类簇,但是与Li相似度距离小于等于dc范围内存在其他类簇的轨迹线段,则轨迹线段Li属于外围区域。 定义16离群阈值:外围区域的所有轨迹线段里,局部密度的最大值定义为离群阈值,记为ρb。 将各个类簇中局部密度小于ρb的轨迹线段从初步聚类结果中剥离出来,作为离群轨迹线段在轨迹聚类效果中单独显示。 轨迹聚类的最后一个阶段就是可视化显示,该环节决定了轨迹聚类的最终效果。TRACLUS算法没有有效利用类簇之间的关系,仅仅为每个类簇提取了一条代表轨迹,可视化效果难以全面精细反映机动轨迹情况。CTECW算法针对该问题进行了改进,分析了各个类簇之间的后继关系,并利用这些后继关系绘制出首尾相连的多个箭头,提升了聚类精度,突出了轨迹聚类的军事意义。但是CTECW算法计算后继关系的方法,容易造成多个类簇的“后继循环”现象,即“A类簇是B类簇的后继,B类簇是C类簇的后继,C类簇又是A类簇的后继”,这将导致聚类结果的混乱表达。本文提出的CTUW算法构建的类簇具有时间属性和编组属性,无须二次处理即可明确类簇之间的后继关系。 CTUW算法还能对非球形分布的数据样本进行聚类,因此,其聚类得到的轨迹线段类簇可能呈曲线形态。如图10所示,某群队的3个棋子呈纵队方式沿着某道路进行机动,该类簇中的轨迹线段发生时间和地理坐标相近,且均属于同一群队,因此,这批轨迹线段被聚为一类。 图10 轨迹线段聚类后的某个类簇 为了将轨迹类簇信息进行精细可视化,本文在完成聚类后,首先对各个类簇内轨迹线段进行二次DPC聚类,聚类算法依据的距离不再是相似度距离,而是空间距离,以完成对类簇内轨迹线段的二次空间切割,形成多个子类簇;再提取每个子类簇的代表轨迹,包含起点、方向、长度、时间范围和单位总称等信息,最后,绘制战斗经过图中的轨迹内容。 在描述可视化算法前,先明确几个概念。 定义17子类簇:针对类簇内的所有轨迹线段,基于线段之间的空间距离,使用DPC算法对其进行聚类,得到的各个集合称为子类簇。 定义18编组权重:轨迹线段关联棋子在编组结构中的权重,记为γ。顶层棋子编组权重为1,下层棋子编组权重是上层棋子的一半,依此类推。如图6所示,H棋子的编组权重是1,G棋子为0.5,E棋子为0.25,A棋子为0.125。 (10) 定义20子类簇代表轨迹的时间范围和单位总称:为了简洁描述聚类信息,子类簇代表轨迹的时间范围为子类簇中所有轨迹线段发生时间的并集,代表轨迹的单位总称分为简写和全写两种,简写总称为所代表棋子的最近共同祖先,全写为合并单位后的所有棋子名称。如图6所示,棋子A、B、D的单位总称简写为G单位,全写为G单位欠I单位。 基于以上定义,算法具体步骤如下: 1)基于轨迹线段聚类得到的类簇,为每个类簇内部的轨迹线段进行二次DPC聚类形成若干个子类簇,聚类时依据的轨迹线段之间距离不再为相似度距离,而是空间距离; 2)按照定义18和19计算每个子类簇的代表轨迹,包含起点、方向、长度、时间范围和单位总称等信息; 3)将第2)步成果绘制成代表轨迹,将同一个类簇下的多个子类簇形成的代表轨迹进行美化,首尾相连的多个小箭头可以整合为一个弯曲大箭头; 4)为第一次轨迹线段聚类过程中查找到的离群轨迹线段绘制轨迹。 为验证CTUW算法的实际效果,我们采集某款计算机兵棋推演系统的一次推演数据进行红方轨迹聚类,该组数据中包含637个红方棋子,下达了4 328条涉及机动行动的命令。如图11所示,分别展示了CTUW算法运行前的轨迹样本情况和执行算法后的聚类效果。因为使用的兵棋推演系统为六角格地图,原始轨迹锯齿状特性较明显,集中大量绘制锯齿状轨迹将干扰展示效果,所以图11a)展示的是基于原始轨迹进行轨迹压缩后形成的简化轨迹。 图11 不同算法执行后的轨迹聚类效果图 从CTUW算法的轨迹聚类效果来看,图11c)能够实现轨迹线段的聚类,并且在可视化表现上能够为代表轨迹赋予关联棋子总称和时间信息,能够支持机动态势的动态展示。进一步分析如下: 1)在处理异常机动速度方面,位于图11b)的D区是炮兵群棋子由西向东间歇性机动轨迹,该群队原地开火一段时间后就转移一次阵地,因此,该群队的轨迹停留点比例较高,CTUW算法不仅能剔除大量冗余的停留点信息,还能准确识别并聚类这种短停频率较高的轨迹。 2)在处理特殊轨迹形态方面,图11b)的E区为右翼攻击群的机动轨迹,H区为侦察队的机动轨迹,右翼攻击群在推演后半阶段分为两路的情况在图11c)中得到体现,零散、细碎、轨迹较多的侦察队在大多数聚类算法中容易被聚类到轨迹线段较长的E或者G区域,但是CTUW算法较好地将其聚为独立的一类。 3)在轨迹交叉方面,图11b)中A区为左翼攻击群,B区为纵深攻击群,C区为推演前半阶段的左翼攻击群和推演后半阶段的纵深攻击群,从图11c)可以看到,CTUW算法能够将C区域内空间重叠但时间不同的轨迹进行区分聚类;图11b)中F区为空军航空兵的航线轨迹,该轨迹与E区的右翼攻击群轨迹非常靠近,但是因为CTUW算法考虑了编组关系距离,所以没有错误地将其与右翼攻击群轨迹聚为一类;图11b)中G区为陆航队航线,该轨迹与F区域的后半段重合,但是CTUW算法依旧能将这两个群队的轨迹区分进行聚类。 因此,CTUW算法不仅能够简洁地概括轨迹动态变化情况,还能同时满足轨迹精细聚类的要求。 从运行效率来看,CTUW算法需要时刻维护和更新距离矩阵,算法运行测试数据样本的主要耗时集中在数据初始化阶段。因为该算法主要作为兵棋推演系统的构件发挥作用,所以实际应用该算法时能够直接读取已经存放于计算机内存中的推演数据,耗时最大的数据初始化环节无需考虑时间代价,轨迹压缩、轨迹线段聚类和可视化这3个阶段的算法复杂度分别为n、O(n·log(n))和O(n·log(n)),CTUW算法的总体时间复杂度为O(n·log(n))。 从算法泛化能力来看,虽然CTUW算法涉及时间、空间和编组关系等多维度的距离,但是算法能够适应六角格地图、矢量路网地图和普通地图上形成的多种轨迹描述类型,还能兼容各类作战编组形式。CTUW算法执行聚类前对3个维度的距离数据的归一化处理,也解决了各组兵棋推演数据的规模、时长和地幅面积差异性较大的样本问题[19],而且CTUW算法采用的DPC聚类框架,无需先验知识,仅需人工设置1个阈值,降低了应用该算法的难度。另外,CTUW算法关于时间、空间和编组关系等维度距离的权值,可由用户通过交互界面进行个性化设置,以满足不同轨迹聚类需求。 轨迹聚类技术不仅直接决定了兵棋推演系统等指挥训练系统的推演效率,还对指挥员基于信息系统进行作战指挥具有较大影响。本文基于时空和编组关系距离,引入DPC聚类算法框架,提出了满足军事应用需求的可视化显示方法,通过具体实例分析,验证了该轨迹聚类算法可行性,为指挥员和指挥机构高效组织兵棋推演发挥了重要作用。



2.2 相似性度量


2.3 轨迹线段聚类



2.4 聚类效果可视化


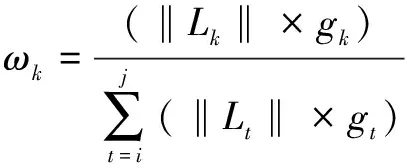
3 实验分析

4 结束语
