基于改进遗传算法的多弹混合瞄准点优化
2023-02-19周于翔舒健生郑晓龙
周于翔,舒健生,郑晓龙,郝 辉,武 健
(火箭军工程大学,陕西 西安 710025)
随着科技的不断发展,常规导弹的弹型和数量不断增多。按照其装药成分的差异,弹头通常分为核弹头、常规弹头和特种弹头等。不同的弹头具有不同的杀伤机理,会造成不同的毁伤效果。作战时,对同一目标采用具有多种毁伤效应的导弹进行打击,将造成复合的毁伤效应,可能会取得更好的打击效果,使目标修复更加困难。
因此,在今后的战争中,我们面临的将不仅是单弹打击问题,更是多数量、多弹型导弹的混合火力打击问题。优秀的打击方案不仅要达到相应的毁伤效果,而且要尽可能节约弹药,提高作战效费比,用最少的代价获得最大的毁伤效果[1]。导弹的瞄准点选择与其造成的毁伤效益直接相关,如果瞄准点位置选择恰当,就可以节约武器用量,用较少的导弹完成作战任务。因此,需预先对瞄准点进行优化,得到各枚导弹的最优瞄准点。
二维平面瞄准点的选择过程是一种多峰性质的非线性函数寻求最优解的问题。传统的寻优搜索算法(如禁忌搜索算法、爬山算法和步长加速法)容易使结果陷入局部最优,且算法的效率和精度都不高[2]。本文采用改进遗传算法对各枚导弹的瞄准点进行全局寻优,将求得的总毁伤价值指标与平均相对毁伤面积指标进行归一化处理,再按权重统一为变电所目标的整体功能下降指标,通过计算该指标的最大值,确定各枚导弹的最优瞄准点[3]。
1 目标分析与毁伤指标模型
1.1 变电所目标分析
变电所是电力系统中变换电压、接受和分配电能、控制电力的流向和调整电压的电力设施,它通过变压器将各级电网连接起来[4]。变电所中起变换电压作用的是电力变压器,另外,还有配电装置、控制设备、保护装置、调度通信装置与补偿装置等设备。
主控楼内设监视、控制和保护变电所一次设备和二次设备的装置。其主体一般为大量梁、柱共同搭建的框架结构,所占空间不大。由于存在较多精密电子设备,被打击后修复较为困难,可视为重要点目标。
电力变压器是变电所的主要设备,负责调整电压[5]。该目标体积小,易损。一般情况下,该目标损毁后以新设备进行替换,可视为重要点目标。
露天开关控制输电线路的通断,同时,对主变电压器起保护作用[5]。露天开关对变电所的重要程度一般,其数量较多,体积较小,可视为点目标,损毁后恢复相对容易。
变电所中的输电线通常呈大面积网状分布,可视为面目标。若电线短路可能产生连锁反应,使主变电压器损坏,并且,因短路产生的电火花可能造成变电所二次毁伤[6]。因此,可对变电所内点目标如主控楼、变压器和露天开关进行打击;同时,可对面目标如电网线路进行打击。
1.2 弹目匹配分析
整体爆破弹的装填系数非常大,战斗部的高爆炸药引发后,将产生高温高压的爆炸物,使周围的气体形成剧烈压缩,从而形成冲击波,并对目标产生损伤。这种弹头比较适合对付轻装甲目标和建筑物。前文提出的主控楼、变压器、露天开关都适合使用这种导弹进行打击。表1所示为目标分析与武器选择。

表1 目标分析与武器选择
石墨弹的战斗部装药为碳纤维丝。导弹战斗部被引爆时,会将战斗部中预先装填的碳纤维丝抛出。碳纤维丝细微、轻盈,较为顽固,不容易清理,附着到电网线路上会导致电路短路,进而导致电网断电,甚至造成二次毁伤。只要不将其清除,短路现象将持续产生。因此,石墨弹适合用于电网线路打击。
1.3 毁伤指标模型
1)毁伤价值比例指标N1
毁伤价值比例指标是导弹总毁伤价值占目标总价值的比例,从价值的角度反映了该目标的毁伤程度。

(1)
其中:mj为各点目标的价值,j=1,2,…,n;pj为各点目标的毁伤概率,j=1,2,…,n;Mh为目标的总毁伤价值;Mz为目标的总价值。
2)相对毁伤面积指标N2
相对毁伤面积指标衡量的是目标区域毁伤面积占目标总面积的比例。

(2)
其中:Sh为目标毁伤面积;Sz为目标总面积。
3)目标整体毁伤指标H
目标整体性能下降指标H衡量了目标总体性能的损毁程度。导弹主要产生多少种毁伤效应,目标整体功能下降指标就应该被分为多少个部分进行求解。得出各子指标值后,再按照各类毁伤作用对被攻击对象影响力度的差异,对每一指标赋予合适的权重,最后进行求和,得出目标整体毁伤指标值。
本文中,目标整体功能下降指标H由毁伤价值比例指标N1和相对毁伤面积指标N2加权求和得到。
H=C1N1+C2N2
(3)
其中:C1、C2为子毁伤指标的权重系数。
2 基于改进遗传算法的瞄准点优化模型
遗传算法以随机搜索的方式模拟自然进化的过程,通过选择、交叉和变异等遗传操作进行目标函数的整体搜索寻优,进而得出最优结果[7]。它的主要特征是直接处理结构对象,对函数连续性没有限制,具有隐式并行性,整体优化能力更突出。
2.1 模型编码规则
本文所建立的瞄准点选择模型是一个二维的多峰值优化问题。考虑问题求解中实际操作的便捷性和求解效率,本文采用双精度实数编码。对于本问题,n枚导弹的瞄准点为(xm1,xm2,…,xmn),(ym1,ym2,…,ymn),则编码为xm1xm2…xmnym1ym2…ymn。
2.2 群体的产生与多样化处理
初始群体的基数越大,群体越具有代表性,运算得到最优解的可能性就越大。但群体基数过大又会导致运算量的增加,使算法效率降低。因此,我们需要选取适当数量的初始群体,记为num,并且要尽可能增加群体的多样性,避免陷入局部最优。本文拟定num=100,运用随机数方法产生种群的初始个体。
在进行选择操作前,将所有个体进行比较,相同基因位的相同基因的量<50%的个体组成新的群体,确保群体的多样性,防止算法产生“早熟”现象[8]。
2.3 瞄准点选择模型
当导弹的战术指标、技术指标与毁伤效应确定时,其对目标造成的毁伤应该按相应的毁伤效果指标进行计算,且指标值的大小仅与瞄准点的坐标有关。比较该枚导弹在各瞄准点的毁伤效果指标值Mk的大小,Mk最大的点是该导弹的最佳瞄准点。本文中,混合火力打击进行混合指标整体优化时,Mk的值是目标整体功能的下降指标H。

(4)
其中:Lxl、Lxr、Lyd、Lyu分别为目标区域的左边界、右边界、下边界和上边界。
2.4 遗传算子设计
遗传算法中常用的遗传算子包括选择算子、交换算子和变异算子。
1)选择算子
选择算子的作用是保留优势解,淘汰劣解。如今遗传算法中常常选择既简单又方便的轮盘赌选择法作为选择算子。轮盘赌选择方法是一种以个体适应度大小为指标的随机选择手段。个体的特征被遗传至后代的概率与其适应度值在总群体里所有个体的适应度值的总和中所占比重相对应。但这种方法具有随机性,可能造成算法中优势个体的丢失,从而陷入局部最优。
因此,本文在采取轮盘赌选择法前,将每代最优秀个体存放在经验池中,之后将某个体i所拥有的适应度值表示为Mi,借助式(5)就能求解出它被选中的概率。将劣势个体淘汰后,若群体数量不够,则从经验池中抽取优势个体进行补充。

(5)
2)交叉算子
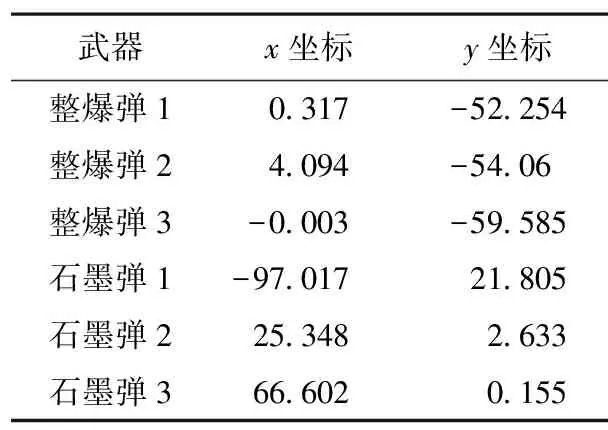
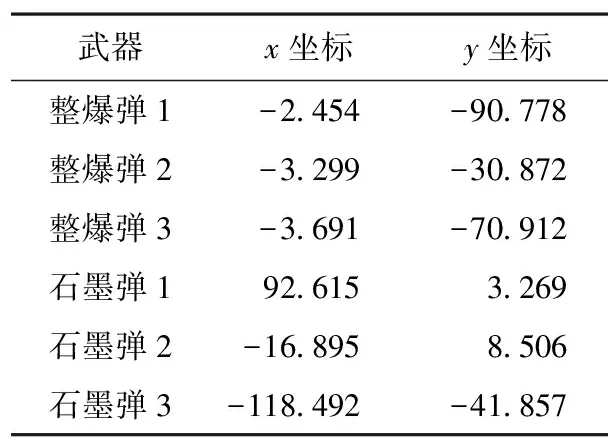
交叉操作的含义是指两个将要进行交叉行为的染色体按交叉概率以一定的形式进行部分基因的置换,并生成两种全新的个体。交叉属于融合算法体系里生成新个体的基本模式。目前,常用的交叉算子有单点交叉、多点交叉、整体算术交叉等[9]。为适应此问题的一些基本特征,本文选择两点交叉的方法来处理。首先,对种群设定杂交概率(本文设定为0.8),即种群中0.8*num的个体可以进行交叉操作。再对将要进行交叉的两根染色体以随机形式确定两个交叉位置a1、a2(1 3)变异算子 变异操作就是用该基因座所含的另一等位基因取代原有基因值的过程。本文采用以下基本位变异:首先,设定变异概率P=0.05,判断是否需要进行变异操作;然后,设定随机数,确定将要进行变异的基因座。 确定最大遗传代数Gm,在经过n次迭代后,若适应度无明显提高,则算法终止。否则,将继续种群进化,直到迭代至Gm代。 第一步,计算目标总价值Mz。按点目标的重要程度将打击范围内的k个点目标赋值为(m1,m2,…,mk),并通过公式(6)进行求解。 (6) 第二步,计算各点目标的毁伤概率pj。若不计系统误差,导弹弹着点散布规律为圆正态分布[10]。记各导弹的毁伤半径为(R1,R2,…,Rn),CEP为(CEP1,CEP2,…,CEPn),瞄准点的横纵坐标分别为(xm1,xm2,…,xmn),(ym1,ym2,…,ymn),对各点目标的毁伤概率为(p1,p2,…,pk)。本文采用蒙特卡洛模拟方法计算一波次导弹打击后每个点子目标的毁伤概率。 首先,利用蒙特卡洛模拟法依次产生各枚导弹的弹着点[11]。首先产生(0,1)的随机数η1(0,1)、η2(0,1),再代入下列公式,根据各导弹的瞄准点坐标(xmi,ymi)计算其落点坐标(xhi,yhi)。 (7) CEP=1.1774σ (8) 然后,判断各点子目标是否被毁伤,进而计算该波次导弹打击后的总毁伤价值。根据公式(9)依次判断各点目标是否被各枚导弹的毁伤圆(以弹着点为圆心,以R为毁伤半径的圆)覆盖。若该点目标被某枚导弹毁伤圆覆盖,则该点目标被有效毁伤。反之,则未被毁伤。记各点目标被毁伤次数为Nj。若判定点目标j被命中,则标记值Nj++。 (9) 其中:(xj,yj)为点目标的坐标值,j=1,2,…,n;Ri为该导弹的毁伤半径。 最后,重复进行N次蒙特卡洛模拟,由公式(10)计算各点目标的毁伤概率。 (10) 第三步,计算毁伤价值比例指标N1。先根据公式(11)计算总毁伤价值指标值Mh,最后,对该指标进行归一化处理,得到毁伤价值比例指标N1。 (11) (12) 平均相对毁伤面积指标是指对面目标造成的平均毁伤比例,即毁伤部分占矩形面目标总体面积的比例N2。 首先,需要对面目标进行离散化处理,使其转化为若干数量点的集合[12]。 然后,与毁伤指标N1的计算相似,采用蒙特卡洛模拟法产生各枚导弹的弹着点。被导弹毁伤圆覆盖的区域为有效毁伤区。在所有导弹打击后,统计矩形目标内被毁伤圆覆盖的点的总个数SUMd,被毁伤点不重复计数。在计算机重复进行N次模拟后,利用公式(13)计算面目标的平均相对毁伤面积指标N2: (13) 目标毁伤指标计算流程如图1所示。 图1 毁伤指标计算流程 本文中,目标整体功能下降指标H由两个子毁伤指标计算得到。两个指标分别为:1)总毁伤价值占点子目标整体价值之和的比例N1,2)目标毁伤部分面积占矩形面目标总体的面积比例N2。 H=C1N1+C2N2 (14) 其中:C1、C2为子毁伤指标的权重系数。 遗传算法的作用主要在于产生瞄准点,并根据毁伤指标的大小淘汰值小的瞄准点,保留值大的瞄准点,并以一定的规则产生新的瞄准点,实现算法的全局寻优,如图2所示。 图2 遗传算法流程图 本次的打击目标为400 m×300 m的矩形目标。如图3所示,变电所中的重要点子目标有主控楼、电力变压器和露天开关。以矩形中心为坐标原点(0,0),以矩形长边为x轴、短边为y轴建立平面直角坐标系。记矩形目标左、右、上、下边界分别为Lxl=-200 m,Lxr=200 m,Lyu=-150 m,Lyd=150 m。 图3 变电所处理图 其中,主控楼共1个,坐标为(0,0),其价值为20。电力变压器共13个,其价值为10,如表2所示。露天开关共13个,其单个价值为5,如表3所示。 表2 电力变压器坐标及其价值 表3 露天开关分布坐标及其价值 本文中导弹武器的数量和参数是已知的,其中,用于打击重要点子目标的整体爆破弹3枚,用于打击电线网路面目标的碳纤维弹3枚,共计6枚导弹,其主要战术技术指标参数如表4所示。 表4 导弹武器参数表 在以目标整体功能下降指标为适应度函数的计算过程中,本文对比使用改进后的遗传算法和传统的遗传算法进行寻优的不同之处,比较两者的优劣,并使用Matlab分别进行仿真和结果输出。最后,使用OriginPro 2021进行数据处理与绘图。如图4所示。 图4 改进后寻优结果图 1)改进遗传算法寻优 迭代51代后,种群适应度值趋于稳定,达到迭代的终止条件,得到最优目标函数值为0.211 2。 结合表5可知,3枚整体爆破弹瞄准点分别位于y轴的左、中、右,都比较接近电力变压器。这是因为在电力变压器附近的价值密度较大,左、中、右三枚弹可以覆盖更多的电力变压器。同时受主控站的影响,三枚导弹的瞄准点有偏上的趋势,且集中于y轴。 表5 改进后瞄准点坐标 由结果可知,3枚石墨弹的瞄准点较为分散。这是因为导弹弹量偏少,为了较好地覆盖更多的区域,需要减少导弹重复毁伤区域的面积。 本实验中,对目标造成的毁伤效果进行了归一化处理。因此,变电所的整体目标价值为1。经计算得出目标整体毁伤效果指标为0.211 2,这是因为变电所目标范围较大,3枚碳纤维弹对该目标的覆盖范围有限;且变电所内点子目标的数量较多,3枚整体爆破弹对点目标的毁伤能力有限,导致对目标造成的整体毁伤效果有限。在作战运用中,应该按实际情况加大各类型导弹的用弹量,才能对目标造成较好的毁伤效果。 2)传统遗传算法寻优 迭代51代后,种群适应度值趋于稳定,达到迭代的终止条件,得到最优目标函数值为0.205。 结合图5与表6可知,改进前的遗传算法优化得出的瞄准点与改进后的遗传算法得出的瞄准点相比,整体爆破弹的瞄准点位置偏下、偏左,位置分布不均匀,得出的毁伤效果相对较差。石墨弹由于数量较少,两种算法都尽可能使其相对分散,则可以覆盖尽可能多的面积。 图5 改进前寻优结果图 表6 改进前瞄准点坐标 从图6可以看出,改进遗传算法比改进前得出的最大目标整体功能下降指标相对较高,而且算法稳定性相对较好。两者收敛速度相近,但总的来说,改进后的遗传算法的效率更高。从两者指标值的对比中可以看出,两者的最大毁伤指标值相近,这是因为用弹量较少,对变电所造成的毁伤效果有限。当弹量增加后,两者指标值会有明显的差别。 图6 最优值对比图 多弹型导弹混合火力打击某一复杂面目标的瞄准点优化问题是近年来导弹火力运用研究领域的一个重点与难点。本文根据目标易损性分析设定了目标的关键点子目标。依据目标自身的特点,采用不同的毁伤效果指标进行计算,给出了目标整体功能下降指标值的计算模型,并利用改进遗传算法进行瞄准点的全局寻优。算例结果表明,对于混合火力打击的瞄准点寻优问题,改进遗传算法的混合指标整体寻优得出的结果更优。该算法有良好的收敛性,具有比较高的应用价值,为今后求解此类问题提供了一种方案。 多弹型常规导弹混合火力打击其他目标的问题与该分析方法相似,可依据实际情况使用合适弹型的导弹,采用合适的毁伤效果指标作为目标函数。最后,通过此算法进行瞄准点的寻优。 本文所建立的模型也存在不足之处,以专家咨询的方式得到的各毁伤效果指标的权重值具有很强的主观性,是一组经验数据。后续研究可对其进行改进,采用更好的权重赋值的方式,减少主观因素的干扰。今后还可以对不同毁伤效果之间存在的耦合关系进行研究。同时,该算法优化速度慢,耗时长,在后续研究中可对其进行改进,在保证计算结果的精确度和稳定性的基础上,尽可能加快其优化速度。2.5 算法终止
3 多弹混合瞄准点优化计算流程
3.1 毁伤价值比例指标N1的计算



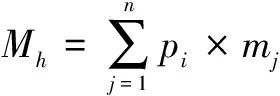

3.2 平均相对毁伤面积指标N2

3.3 目标整体毁伤指标H

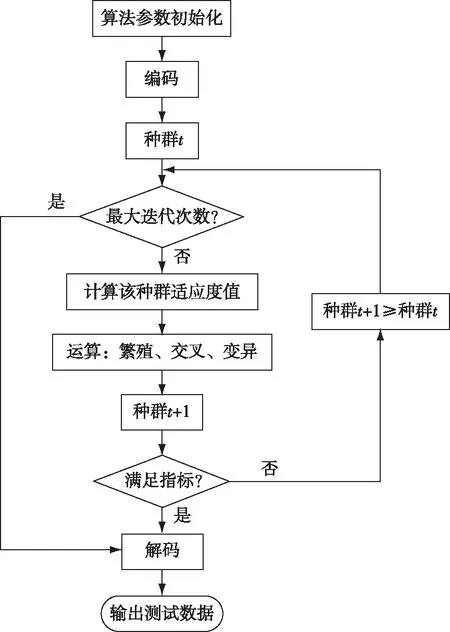
3.4 遗传算法流程
4 示例分析
4.1 变电所目标的数据


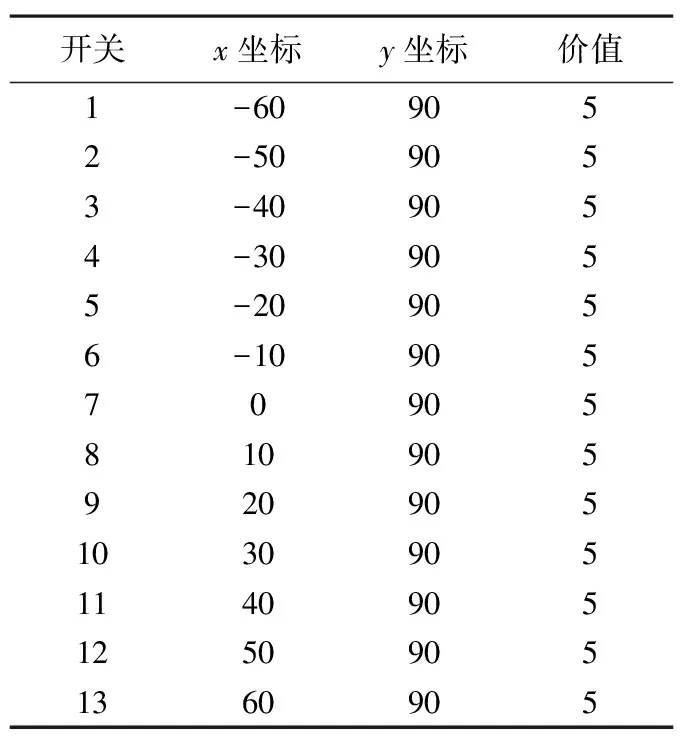
4.2 导弹武器的参数

4.3 示例计算
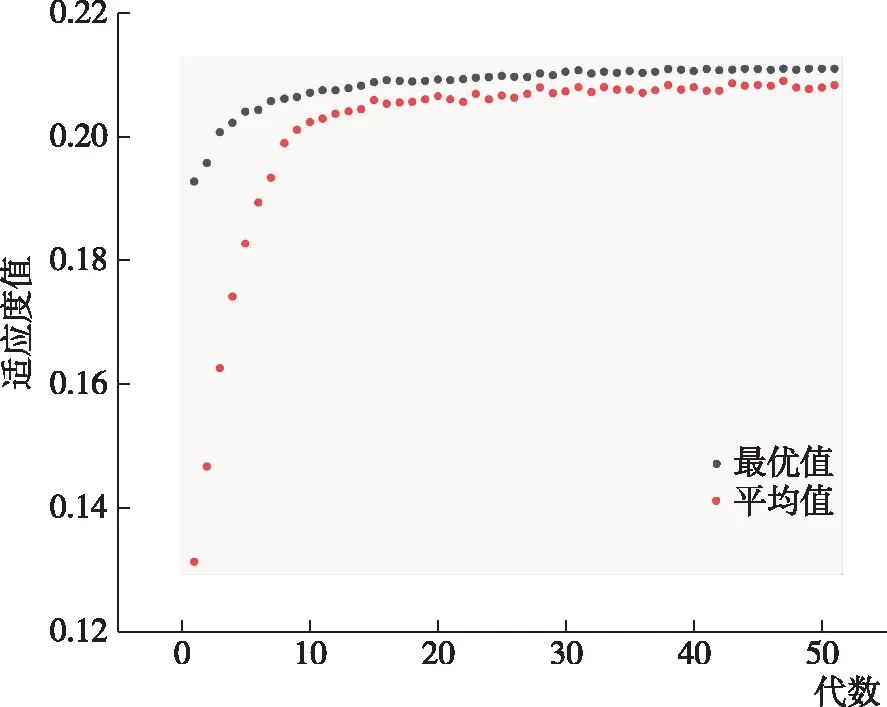

4.4 结果比较

5 结束语
