基于滑模观测器的LCL型并网逆变器鲁棒预测控制研究

2023-02-19高鹏飞郑铭哲郭磊磊李琰琰

智慧电力 2023年1期

高鹏飞，郑铭哲，郭磊磊，李琰琰，金楠，黄春

（郑州轻工业大学电气信息工程学院，河南郑州 450002）

0 引言

随着风能、太阳能等可再生分布式新能源技术的迅速发展，新能源并网逆变器已成为电力电子领域研究的热点[1-3]。逆变器是新能源发电的核心设备，其并网控制技术是新能源发电的核心技术。有限控制集模型预测控制（Finite Control Set Model Predictive Control，FCS-MPC）在并网逆变器控制方面具有巨大的发展潜力[4-7]。但FCS-MPC 的控制性能易受参数变化和模型不确定性的影响[8-11]，导致并网电流控制存在偏差。在实际工程应用中，电抗器饱和、温度变化或电气元件老化都会影响FCS-MPC的控制精度[12]。

国内外学者就如何提高模型预测控制的参数鲁棒性进行了一定研究。文献[8-12]就模型参数变化对电流预测控制的影响进行了分析，从理论上证明参数不匹配时电流控制误差将增大。文献[13-14]提出一种自适应周期性模型参数调整策略，解决了系统模型参数偏差，提高了模型预测的准确性，缺点是系统的运算量较大。文献[15]通过研究并网逆变器的电感辨识方法以实现鲁棒FCS-MPC 控制，但其电感辨识精度较低。文献[16]利用梯度优化的自适应在线参数辨识方法进行实际滤波参数辨识跟踪，可提高并网控制的稳定性，避免模型参数误差对并网电流质量的影响。

为了彻底解决并网逆变器FCS-MPC 对参数的依赖，大量学者基于超局部建模理论的无模型预测控制进行了广泛的研究。文献[17]首次提出无模型预测电流控制，其优点在于计算简单且易于实现。文献[18]提出一种新型无模型预测电流控制方法，具有较强的参数鲁棒性，但所涉及算法对系统的处理器要求较高且计算量较大，不具备实际操作性。文献[19-20]采用无模型预测控制策略计算超局部模型中的关键变量，使用代数辨识技术[20]（超局部模型为二阶，即含有2 个关键变量）提高系统的参数鲁棒性，缺点在于使用了大量采样值增加了系统的计算负担。目前，解决无模型预测控制方法运算复杂的问题是当务之急。

综上所述，本文利用超局部建模理论，提出一种基于滑模观测器的LCL 型并网逆变器鲁棒预测控制方法。该方法将文献[20]中的二阶超局部模型等效为一阶超局部模型（即只含有1 个关键变量），使用滑模观测器代替代数辨识技术对系统的集总扰动进行估计，减少了控制系统的计算负担，提高了控制系统的稳态性能和动态性能，解决了并网逆变器FCS-MPC 对参数的依赖性，实现了并网电流的无模型鲁棒预测控制，具有很强的实际应用价值。

1 常规LCL型并网逆变器预测控制

1.1 LCL型并网逆变器数学模型

典型的LCL 型并网逆变器拓扑结构如图1 所示。

图1 LCL型并网逆变器拓扑结构Fig.1 Topology of grid-connected inverter with LCL filter

图1 中，udc为直流侧电压，S1-S6分别为并网逆变器的6 个开关，L1，L2分别为逆变器侧电感和网侧电感，C为滤波电容，R1，R2分别为L1和L2的寄生电阻，Rc为无源阻尼电阻，uoa，uob，uoc分别为a，b，c三相逆变器输出电压，uca，ucb，ucc分别为a，b，c三相滤波器电容电压，ua，ub，uc分别为a，b，c三相电网电压，i1a，i1b，i1c分别为a，b，c三相逆变器侧电流，iga，igb，igc分别为a，b，c三相并网电流。

在静止αβ坐标系上，LCL 型并网逆变器的数学模型为：

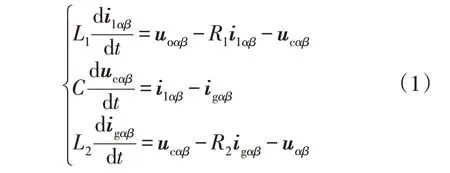
式中：i1αβ和ucαβ分别为静止αβ坐标系上的逆变器侧输出电流矢量和滤波电容电压矢量；igαβ和uαβ分别为静止αβ坐标系上的并网电流矢量和电网电压矢量；uοαβ为逆变器输出的电压矢量；t为单位时间。

根据式（1）所示的数学模型，采用前向欧拉差分法进行分步预测，在静止αβ坐标系上建立预测电流控制模型为：

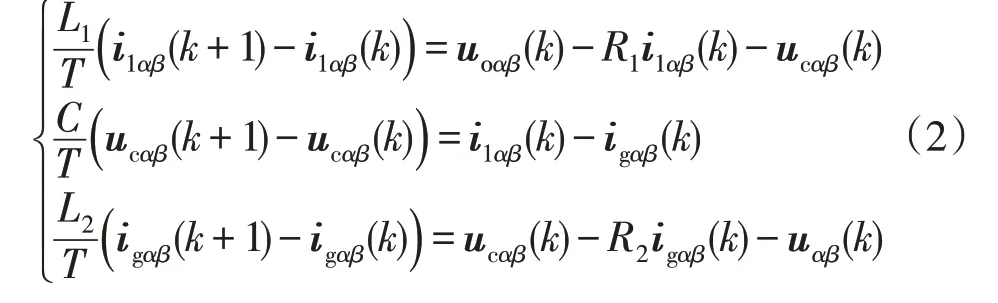
式中：T为采样周期；i1αβ(k+1)，ucαβ(k+1)，igαβ(k+1)分别为k+1 时刻逆变器侧电流矢量、滤波电容电压矢量和并网电流矢量的预测值；uοαβ(k)，i1αβ(k)，ucαβ(k)，igαβ(k)和uαβ(k)分别为k时刻在静止αβ坐标系上采样的逆变器输出电压矢量、逆变器输出电流矢量、滤波电容电压矢量、并网电流矢量、电网电压矢量。

在FCS-MPC 过程中存在采样步长延时，可根据式（2）采用uoαβ(k)的计算原理预测k+1 时刻的电流和电压，再根据uοαβ(k+1) 以及i1αβ(k+1)，igαβ(k+1)，ucαβ(k+1)的预测值对k+2 时刻的并网电流矢量igαβ(k+2)进行预测，其表达式为：

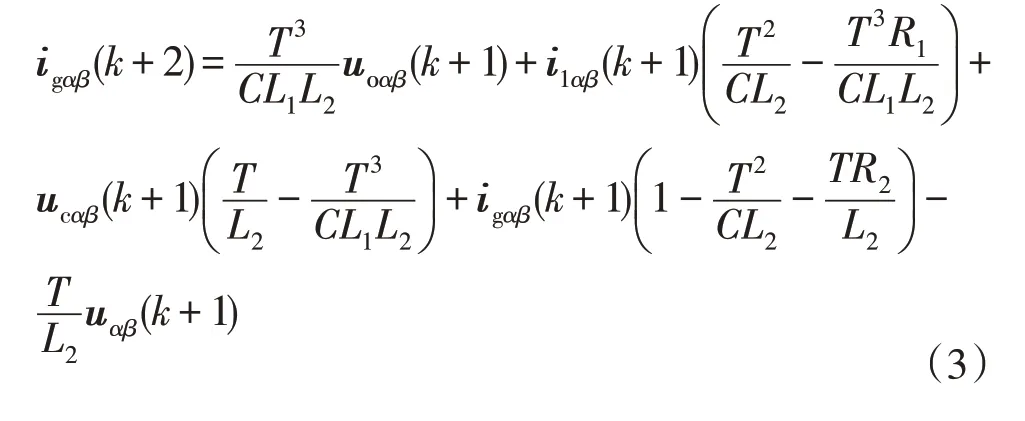
考虑到并网逆变器控制过程中采样频率较高、电网电压变化较慢，可推导出k+1 时刻在静止αβ坐标系上的电网电压矢量uαβ(k+1)近似等于uαβ(k)。在执行FCS-MPC 算法时，通常将式（3）的预测结果带入式（4）所示的代价函数M，通过比较寻优，确定M的最小值所对应的电压矢量作为最优电压矢量，并将其用于控制LCL 型并网逆变器。代价函数M的表达式为：

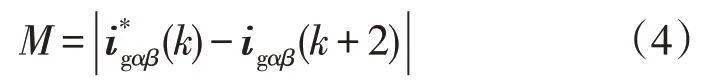
1.2 参数失准灵敏度分析

由式（2）可知，常规模型预测电流控制方法取决于模型的精度，当滤波器模型参数与实际滤波器参数不匹配时，控制误差将增大。为分析参数失准对常规并网电流预测控制的影响，定义参数误差为EL1=L1C-L1，EC=CC-C，EL2=L2C-L2，其中EL1，EL2，EC分别为逆变器侧电感误差、网侧电感误差和滤波电容误差，L1C，L2C，CC分别为控制器中使用的逆变器侧电感、网侧电感和滤波电容。将式（1）改写为：

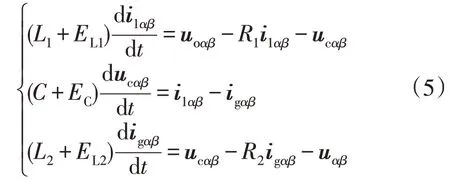
对式（5）进行离散化，得到参数失准情况下k+1时刻的并网电流矢量。当逆变器侧电感、网侧电感和滤波电容参数均偏离实际滤波电路中的L1，L2，C时，根据文献[8]定义并网电流预测控制误差EΔξ为：

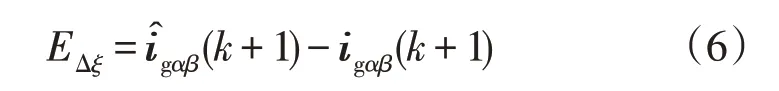
在LCL 滤波器的3 个参数均不匹配的情况下，参数失准时电流误差效果图如图2 所示。

图2 参数失准时电流误差效果图Fig.2 Diagram showing current error effect of parameter mismatch

由图2 可知，当模型中电感电容参数匹配时，几乎不存在电流预测控制误差（图2 中深蓝色部分）；当L1，L2，C的值均减小时电流预测控制误差（图2 中的红色部分）最大值超过了2 A。特别是当参数L2，C的值越小时电流预测误差越大，可知3 个参数中L2和C对电流预测误差的影响更大。

常规FCS-MPC 的主要缺点是对模型参数的依赖性较高，即预测电流的控制精度与电路模型参数精度密切相关。一旦控制模型的参数与实际电路参数不匹配，就会产生预测控制误差，进而降低电网电流的电能质量。综上，提高预测控制精度，研究LCL 型并网逆变器输出电流的鲁棒预测控制方法是十分必要的。

2 LCL型并网逆变器鲁棒预测控制

2.1 超局部建模和并网电流预测控制

基于超局部模型理论的并网电流预测控制是解决FCS-MPC 对参数依赖性问题的有效方法。因此，本文研究了基于滑模观测器的LCL 型并网逆变器的超局部建模方法和并网电流的鲁棒预测控制方法。

对式（5）进行离散化，可得并网电流状态方程为：

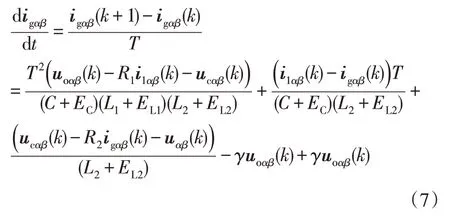
根据超局部建模原理，式（7）可进一步改写为：

式中：γ为设计超局部模型时采用的电压和电流比例系数，通常设置为1/L1L2C；Zαβ为集总扰动矢量。

本文所提的一阶超局部模型通过引入Zαβ和γ，即可解决由高阶系统的耦合作用而导致的建模复杂性问题。对式（8）进行离散化，得到并网逆变器的一阶超局部预测模型为：

在一定程度上，这种现象是法官基于其理性进行风险规避的必然结果。在处理侵犯集体财产权的案件时，法官可能面临以下风险：(1)由于无直接依据可资援引，法官需要造法裁判，但农民与法官之间紧张的信任关系容易引发强烈的质疑和反弹；(2)造法裁判意味着法官要主动审查政府的相关涉农政策，大多数情况下要面对行政力量的干扰，可能造成司法权与行政权的直接冲突；(3)由于推行办案质量终身负责制和错案责任倒查问责制等，法官判决越多则风险越高。法官也是风险规避者，自然很难采取积极能动的审判姿态。因此，立法需要明确有关的具体规则，使法官更少地依赖自由裁量和能动司法，更多地依据法律规定进行裁判。

式中：Zαβ(k)为k时刻的集总扰动矢量。

当整个控制系统受到扰动时，需对由γ变化造成的影响进行分析，为基于超局部模型方法的并网电流鲁棒预测控制提供理论依据。当γ出现1 个扰动γ0时，γ0uoαβ为总扰动的一部分，式（8）可进一步表示为：

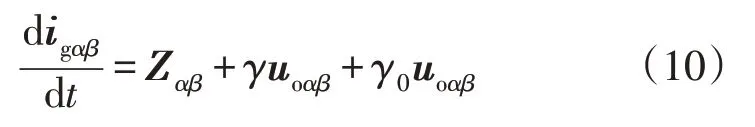
2.2 基于滑模观测器的集总扰动计算方法

由式（9）可知，针对Zαβ的计算是实现并网电流鲁棒预测控制的关键。为了估算Zαβ，本文基于式（8）提出一种基于滑模观测器的Zαβ计算方法。由于并网逆变器控制系统采样频率较高，因此可在控制周期中内得出Zαβ的差分形式，并推导出基于超局部建模的并网逆变器数学模型为：

式中：ω为电网角频率。

为确保观测系统的稳定性，需要正确选择状态观测器的增益系数。由于滑模观测器具有容易设计、结构简单、对参数变化的鲁棒性强[21-23]等优点，所以本文根据式（11）中模型设计滑模观测器来计算Zαβ，所设计的Zαβ滑模观测器为：

对式（12）进行离散化，可得估计的并网电流与集总扰动为：

将式（13）的计算结果带入式（9）即可实现并网电流的鲁棒预测控制。根据李雅普诺夫稳定性原理，对所设计的滑模观测器的稳定性进行判定[24-25]。得出结论为：并网电流滑模观测器的增益K1越大，观测器系统收敛的越快，滑模噪声也随之增大。因此，需要合理选择K1。为进一步研究K1和K2对Zαβ观测的影响，通过分析闭环传递函数的伯德图来对滑模增益进行详细研究。

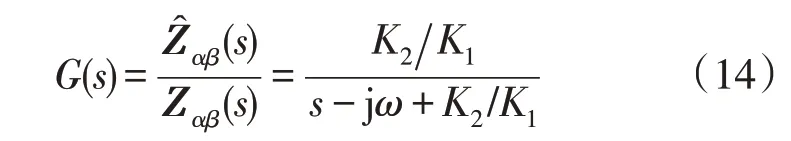
由式（14）可知，当s=jω，时，所提的观测器可准确地估计Zαβ的值。

传递函数G（s）的伯德图如图3 所示。

图3 传递函数G（s）的伯德图Fig.3 Bode diagram of transfer function G（s）

由图3 可知，K1和K2对滑模观测器动稳态性能有一定的影响。当K2/K1增加时G（s）的带宽增加，系统动态响应速度加快，但随着K2/K1的增大，幅频特性曲线高频段衰减变慢，导致滑模噪声放大、滑模观测器的稳态性能变差；当K2/K1减少时G（s）的带宽减小，系统的滑模噪声缩小、滑模观测器的稳态性能变好，但随着K2/K1的减小，系统动态响应速度变慢。结合实验过程调试，最终取K2/K1为75，将K1，K2分别设置为200 和15 000。

2.3 并网逆变器鲁棒预测控制系统结构

本文所研究的基于滑模观测器的LCL 型并网逆变器鲁棒预测控制系统结构如图4 所示。其中，Na，Nb，Nc分别为a，b，c三相并网逆变器的开关状态（值为1 表示上桥臂导通，下桥臂关断；值为0表示上桥臂关断，下桥臂导通）。

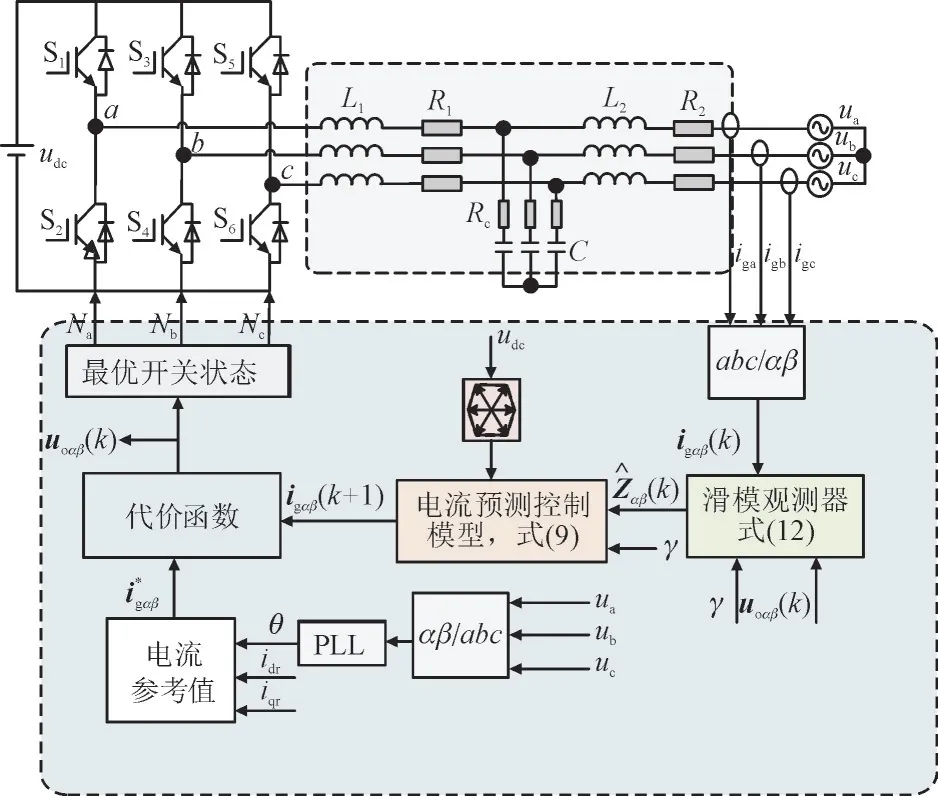
图4 并网逆变器鲁棒预测控制系统结构Fig.4 Robust predictive control system structure of grid connected inverter

由图4 可知，系统中所有的控制变量均通过Clark 变换（三相abc变换到αβ静止坐标系）后进行计算。首先，采样并网逆变器的网侧输出电流用于滑模观测器观测；然后，将带入式（9）计算出并网预测电流，电流参考值可以由有功并网电流参考值idr、无功并网电流参考值iqr和电网电压角度θ计算得出，其中θ由电网电压和锁相环（Phase Locked Loop，PLL）得到；最后，通过代价函数比较寻优，选择最优的电压矢量作为逆变器下一时刻输出电压。本文所提方法无需采样逆变器侧电流和滤波电容电压，因此省去了逆变器侧电流传感器和滤波电容电压传感器，具有简便易行、节约成本、提高系统可靠性等优点。

3 实验分析

为验证所提基于滑模观测器的LCL 型并网逆变器鲁棒预测控制方法的有效性，搭建包括Typhoon602 +仿真器和PE-Expert4 控制器的实验平台。其中控制算法在PE-Expert4 处理器板上执行，该处理器板由DSP 和FPGA 控制芯片组成。实验系统参数如表1 所示。

表1 实验系统参数Table 1 Parameters of experimental system

为验证所提控制方法的有效性以及参数鲁棒性，本文在模型参数失准的情况下，与常规FCSMPC 方法进行了控制性能对比分析。实验中设定有功电流参考值idr为10 A，无功电流参考值iqr为0 A。参数失准（L1=5 mH，L2=50 μH，C=80 μF、）情况下iga的电流波形及控制误差如图5 所示。其中，在t为0～100 ms 时，控制系统采用LCL 型并网逆变器常规FCS-MPC 方法；从t为第100 ms 时开始，控制系统切换为基于滑模观测器的LCL 型并网逆变器的鲁棒预测控制方法。

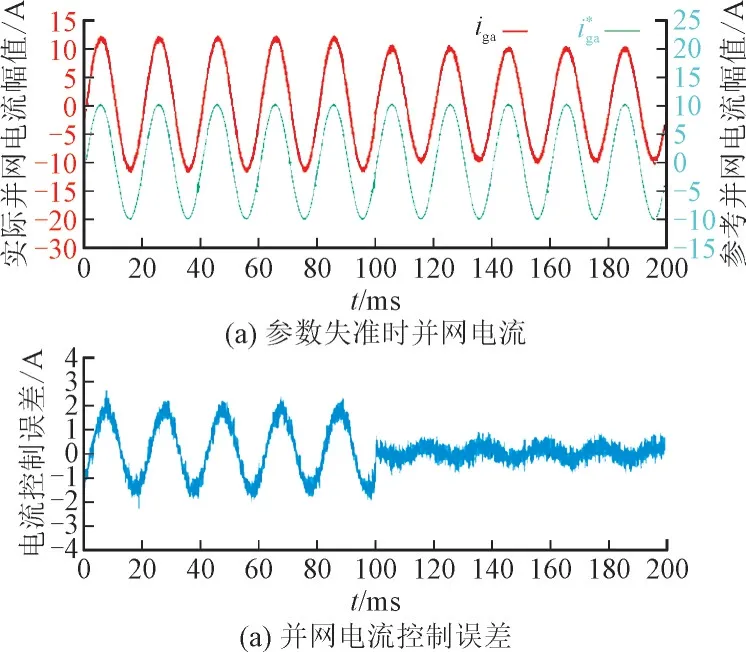
图5 电流波形及控制误差Fig.5 Current waveform and control error

由图5 可知，当滤波电感和电容参数同时偏小时，常规FCS-MPC 方法的并网电流误差波动较大，这与1.2 节的参数失准灵敏度分析相一致。当参数失准时，本文所提方法的并网电流控制误差相对较小，验证了该方法具有较强的参数鲁棒性。

为了证明本文所提基于滑模观测器LCL 型并网逆变器鲁棒预测控制方法的优越性，将文献[17]中研究的基于代数辨识技术的无模型预测控制方法用于本文LCL 型并网逆变器控制系统中。在同等实验条件下（一阶超局部模型只需计算Zαβ），2 种无模型预测控制方法下的稳态控制性能对比如图6所示。其中，在t为0～100 ms 时，控制系统采用基于代数辨识技术的无模型预测控制方法；从t为第100 ms 时开始，控制系统切换为基于滑模观测器的LCL 型并网逆变器的鲁棒预测控制方法。

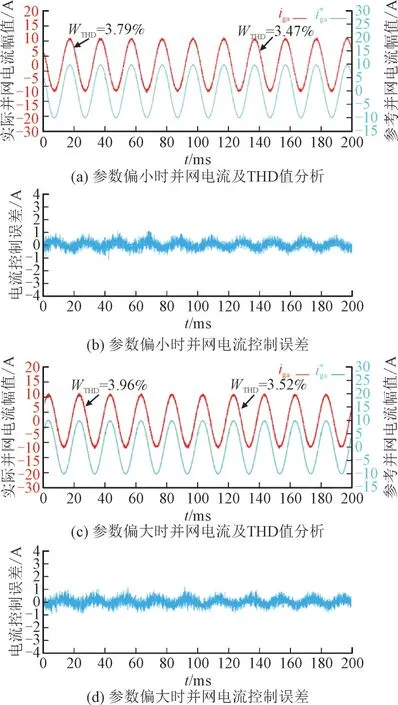
图6 2种无模型预测控制方法下的稳态控制性能对比Fig.6 Comparison of steady-state control performance of grid connected current between two methods without model predictive control

图6 中，图6（a）和图6（b）为参数L1，L2，C同时偏小（L1=5 mH，L2=50 μH，C=80 μF）时的并网电流控制误差和总谐波畸变率（Total Harmonic Distortion，THD）值分析；图6（c）和图6（d）为参数L1，L2，C同时偏大（L1=9 mH，L2=200 μH，C=220 μF）时的并网电流控制误差和THD 值分析。WTHD为THD 的值。

由图6（a）和图6（b）可知，当模型参数同时偏小时，基于代数辨识技术的无模型预测电流控制误差与本文所提控制方法下的电流误差几乎相等，但是基于代数辨识技术的无模型预测电流的谐波较大，THD 值达到了3.79%，而本文所提控制方法下的电流THD 值为3.47%；由图6（c）和图6（d）可知，当模型参数同时偏大时，发现2 者电流误差对比也没有明显变化，但是电流谐波含量都同时增大，特别是基于代数辨识技术的无模型预测电流的谐波较大，THD 值达到了3.96%，而本文所提控制方法下的电流THD 值为3.52%，谐波含量变化较小。对比分析表明，本文所提基于滑模观测器的LCL 型并网逆变器鲁棒预测控制方法具有更好的稳态控制性能。

为进一步比较所提方法与使用代数辨识技术方法的电流控制动态性能，本文在模型参数匹配时进行1 组动态实验。实验设置在t=40 ms 时，有功参考电流idr由10 A 突变为15 A，则并网电流iga的动态控制性能对比如图7 所示。