超声振动铣削淬硬模具钢表面粗糙度理论模型分析

徐凯 张会妨

1.新乡职业技术学院数控技术学院；2.新乡职业技术学院教务处

为了提升铣削淬硬模具钢已加工表面的表面质量，采用在工件上施加超声振动的方法进行超声振动铣削，由于超声振动的存在，刀具对工件进行间断切削，会对已加工表面的质量产生影响，本文主要研究超声辅助铣削淬硬模具钢的已加工表面形成机理和变化规律，分析各种加工要素对表面粗糙度的影响，由此综合实现了对表面粗糙度在理论上建模，经验证，当加工参数及刀具参数保持一致时，采用超声振动铣削能够有效降低被加工工件表面粗糙度值。

机械零件的表面粗糙度对其使用可靠性和使用寿命有重要影响，同时对于配合的零件来说，表面粗糙度对配合性质、耐磨性、疲劳强度、接触刚度、振动和噪声等都有密切关系[1]。因此在保证机械零件尺寸精度的前提下，提升表面质量也同等重要。本文主要研究在超声振动铣削淬硬模具钢SKD61 条件下，机械零件表面粗糙度的变化规律。

1 超声振动铣削运动学模型

超声振动铣削运动学模型的构建是先将超声振动使用在刀具或预制品工件上，在进行机理分析时，需考虑到超声铣削的运行学特性，并以此为基石进行专题说明，而本文试验中的测验内容则是将超声振动作用于预制工件上，其具体铣削运动学模型如图1 所示。

图1 工件超声振动铣削运动学模型Fig.1 Kinematics model of ultrasonic vibration milling of workpieces

预制工件在进行铣削加工时，会处于不衰减简谐振动状态，在A 位置时进给方向与工件振动方向相同，是加工周期起始阶段；在B 位置时，振动方向与进给方向相反，是加工断续阶段。

当工件处于简谐运动状态时，可得工件的位移指标y 存在客观关联关系，用专业公式表示如式（1）所示：

即可知工件的振动速度v可表示为如式（2）所示：

在B 处的t2时刻工件相对与进给是反方向运动，即可得在t2时刻的切削速度如式（3）所示：

那么t2时刻可由上式可求得如式（4）所示：

在普通铣削时，工件不会产生简谐振动，即不存在t2，也就是当v=Aw时，切削速度为临界切削速度vc，且可表示为如式（5）所示：

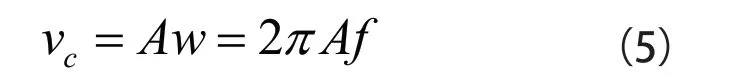
在B处，工件沿切削方向速度为v，可知工件的位移y，如式（6）所示：

在A 处的t1时刻开始切削，工件的位移y如式（7）所示：

由式（6）和式（7）得到如式（8）所示：

若有wt1=2πt1/T、wt2=2πt2/T将其带入（3）得到如式（9）所示：

由式（8）和式（9）得到如式（10）所示：

由此得到如式（11）、式（12）所示：

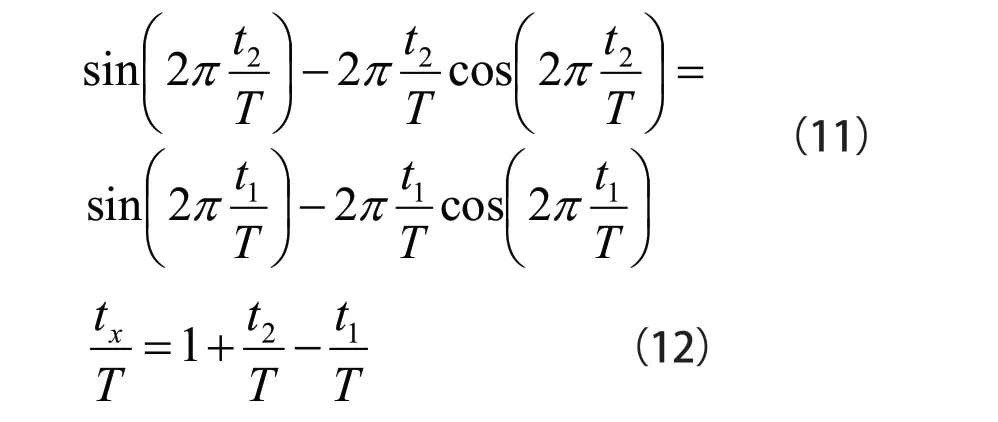
式中T 为振动周期，有T=1/f；tx的含义是阶段时间内的周期切削时间，是非常重要的客观变量；tx/T 为每个振动周期中刀具的净切削时间所占比；从式（12）中可以证明，由于超声振动的存在，其加工为间歇性的切削工艺，有利于进行杂质清理和散热，从而避免实验时出现异常形变或状态变化，进而获得稳定的表面张力，保障工艺的稳步进行[2]。

2 超声振动铣削淬硬模具钢表面粗糙度的理论模型

2.1 材料变形机理分析

淬硬模具钢是硬脆性材料，但在铣削过程中也会发生微小的塑性变形，对此在实验时可将其暂时假定为正处于脆性与塑性间的转变状态，此时将切削厚度设定为hc，在经过多次加工后，其厚度和初始数值相比会有明显的下降，但其表面的结构韧性不会有明显变化，但当其数值接近既定的标准阈值hc时，便会出现塑性和脆性间的状态变化，此时会产生大量的切屑，还会形成多个切削层，整个结构的表面粗糙度影响极高[3]，上述关系中的hc可使用如式（13）和式（14）所示的计算公式来得出数值，并表明其与其他变量间的关系：

式中E-弹性模量（GPa）；H-材料硬度（GPa）；Kc-断裂韧性；ϕ-比例系数；µ-泊松比。

虽说上述结论总结了切削厚度在不同状态下的变化情况，并发现各个变量间存在客观联系，且能够借助专业知识进行数值转化，但工作人员需明确实验物料的种类也会影响后续计算，不同的材料其切削厚度是不同的，当其作用于不同的切削参数环境中时，其临界值也会存在一定的偏差。但任何材料，若其切削厚度大于临界数值，同样会发生脆性转变，物料的稳定结构将被破坏，而且当物料出现脆性变化时，其处理技术和本身的结构破损均会对外形成影响，甚至会将裂纹等延伸至表面。基于此，工作人员在进行试验时需尽可能控制切削厚度，确保其不超过临界厚度值，利用传统的塑性去除工艺进行物料处理，直至表面无裂纹且内部结构稳定后再进行调整，从而影响整体结构质量。但对于本文中主要使用的淬硬模具钢来说，其切削厚度的临界值多会控制在50～200 纳米左右，再加之现代机械加工工艺会涉及到物料的多种状态转换，此时若忽视切削厚度临界值的标准化调整，后续会出现去除工艺效果不明显的风险，但只要并未出现切削厚度明显高于临界值的情况，整体结构的状态也不会发生明显改变，更不会影响已加工材料表面的粗糙度。但若切削厚度长期低于下限阈值数值，材料即使经过塑性去除与调整，物料的结构变化仍会产生不必要的隐患问题，例如表面质量下降或裂纹等[4]。

对此，试验人员为精确获取切削形变区域的材料变化情况，需针对其切削厚度、去除状态进行综合分析，并根据工艺要求和数值，测算临界厚度值hc，并根据当前试验流程得出标准切削厚度阈值的上限和下限，并根据一直的铣削深度及给料量等数值分析各个变量间的客观联系，从而明确切削层的最大厚度hmax 的两类主要状态:

图2 (a) 切削层的最大厚度Fig.2 (a) Maximum thickness of cutting layer

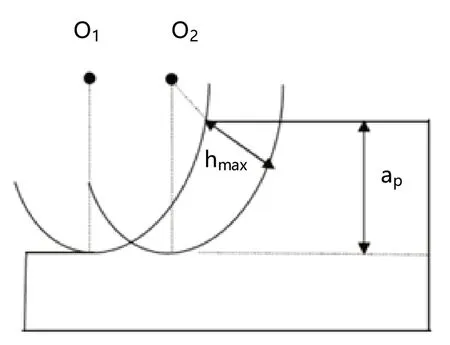
图2 (b) 切削层的最大厚度Fig.2 (b) Maximum thickness of cutting layer

综上，有关人员需明确说明切削厚度一旦超出固定阈值变化发生脆性形变，但只要处于最大厚度状态的材料不与加工表面直接接触，均不会产生异常形变，此时加工表面也不会出现连带性的质量缺陷，这也意味着表面粗糙度的影响较低，微塑性在a p>hc出现。

从上面的分析可以知道，在本研究中对淬硬模具钢超声辅助铣削试验中，可以满足的条件，也就是能够实现了该材料的微塑性变形。

通过分析为塑性形变原理，并结合铣削工艺可知，刀具等工器具在进行加工时，铣削工艺会在工器具上留下多个形变区域，这些区域在理论状态下，会形成独立的切削模型，在此基础上，刀器具已知加工表面在受积压后会形成全新的形变区域，如图3 所示。

如图3 所示，abcd 区域便是上述理论中的第一形变区，而afe 则是第二个形变区，此时考虑到已加工过的表面及时受到外界积压或摩擦后也会存在回弹性，故而刀具和切削刀刃只能造成区域板块的异常形变，却无法形成其他形变区域，除上述两个形变区域外，第三个形变区域只有ahg 板块，其形成的原因是abcd 区域的塑性形变影响，但其粗糙度会存在明显的数值差异，若想确保后续试验的稳步推进，相关人员需进一步进行数值分析与验证。

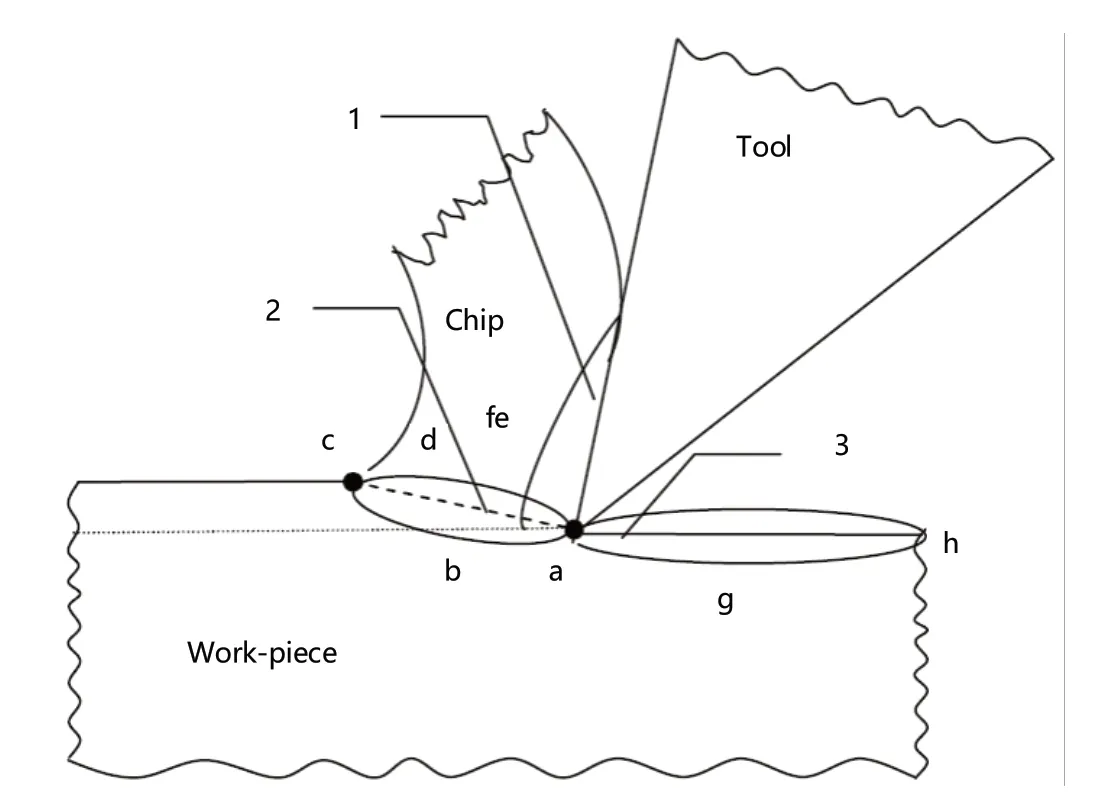
图3 切削过程材料变形区域的简化模型Fig.3 Simplified model of material deformation region during cutting process

2.2 普通铣削表面粗糙度的理论模型

残留面积其高度会受试验器具刀刃和切削相关数值的影响，一般其在理想状态下，粗糙值等数值可依靠控制高度来进行控制。但其确定铣削残留高度的方法基本都是基于估算公式上，原先建立的表面最大残留高度公式并没有考虑到刀具的每齿进给量问题以及超声振幅问题，这里在建立最大残留高度模型考虑铣削宽度D 和每齿进给量fz 的共同影响，得到如图4 所示的工件加工残留高度的计算公式。

图4 最大残留高度Fig.4 Maximum residual height

据图4 所示，左右两个三角形存在客观关联，即：

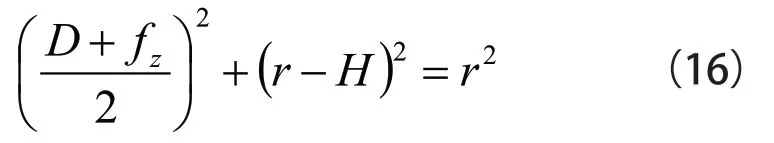
式（16）中r-铣刀半径（mm）；D-铣削宽度（mm）；fz -每齿进给量（mmz）；在实际加工情况可知道，一般有H ＜r,从而可得如式（17）所示的关系式：

在实验过程中，通过对材料的物理特性进行分析，并结合切削工艺的内容后可知，如图4 和图5 所示的客观物理学状态变化可借助塑性形变及物料回弹量的数值差异进行综合分析，即：当刀具向材料靠近，二者由于挤压产生摩擦力时在基点O 处将待切削层和已切削层切开，基点O上面的材料形成切屑并堆积在前刀面上，基点O 下面的待切削层变为已加工表面。但考虑到工件间的摩擦力会产生一部分势能损耗，且相互作用力会促使刃口的钝圆和后刀面与已知试验表面材料发生直接接触，此时材料在经过点N后，受弹性作用力的影响，弹性回复值会带动切削工艺的相关数值发生变化，刀具和加工表面区域agh 会再次出现塑性形变，后续的便面粗糙度也会受到影响[5]。

图5 切削工件表面成形特性简化模型Fig.5 Simplified model of surface forming characteristics of cutting workpiece

在经过妥善的数据分析后，结合分子-机械摩擦理论，可以对切削器具和加工表面的异常塑性形变与弹性作用力之间的客观联系进行探究，并基于现场数值制定简化分析模型，具体情况如图6 所示。此时，工作人员可将与工件直接接触的刀具视为球型，此时其立体半径便是切削厚度，而后当实验促使刀具进行定向切割时，预期直接接触的球体会受挤压出现异常摩擦，进而引发弹性回复和塑性形变等现象并随之产生塑性变形深度hp，刀具离开工件后产生了弹性回复高度he，二者对已加工表面会产生一个塑性流动高度差值h。

图6 工件表面弹塑性变形简化模型Fig.6 Simplified model of elastic-plastic deformation of workpiece surface

塑性流动高度差值h如式（18）所示:

借助Kragelski 摩擦理论中的分子-机械摩擦理论及摩擦计算相关理论，对于实验时出现塑性形变的材料而言，若想借助其现有的数值实现实验运算，工作人员需按照Hertz 弹性接触理论进行理念转换，并考虑形变等数值的变化规律，进一步分析表面层在不同变形程度时的弹性回弹数值差异，具体的回弹高度如式（20）所示：

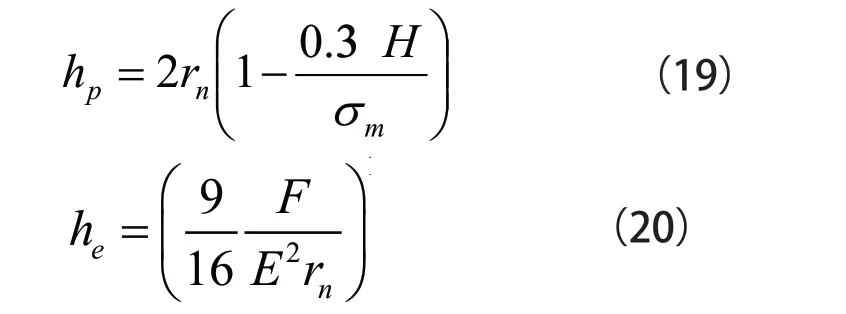
式中rn-刀具的圆弧半径（mm）；H-工件材料的硬度（GPa）；σm-工件材料流动应力（Pa）；E-工件材料的弹性模量（GPa）；F-材料已加工表面在加工时受到了垂直于表面层的压力（N）；

由式（18）、式（19）和式（20）可得到已加工表面微塑性变形对表面粗糙度的影响值如式（21）所示：

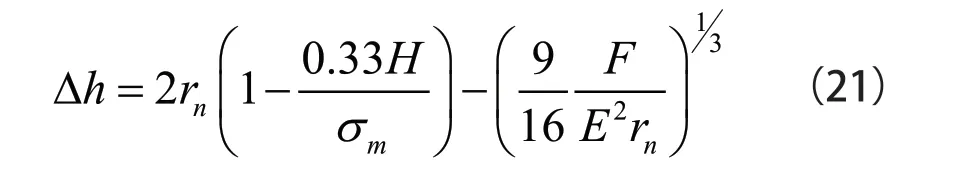
在普通铣削加工下，当只考虑这两部分因素对表面粗糙度的影响时，由式（17）和式（21）可以得到普通铣削加工下表面粗糙度的理论模型，如式（22）所示：

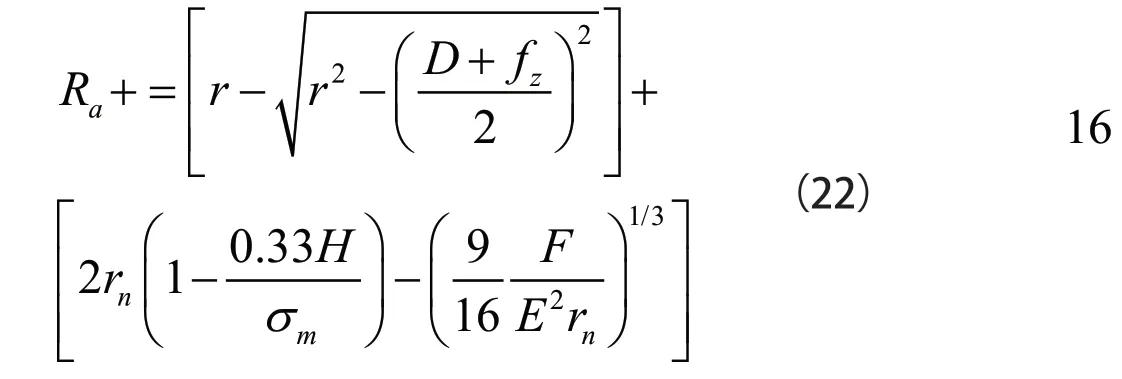
2.3 超声铣削表面粗糙度的理论模型

刀具在超声振动下的速度矢量如图7 所示。

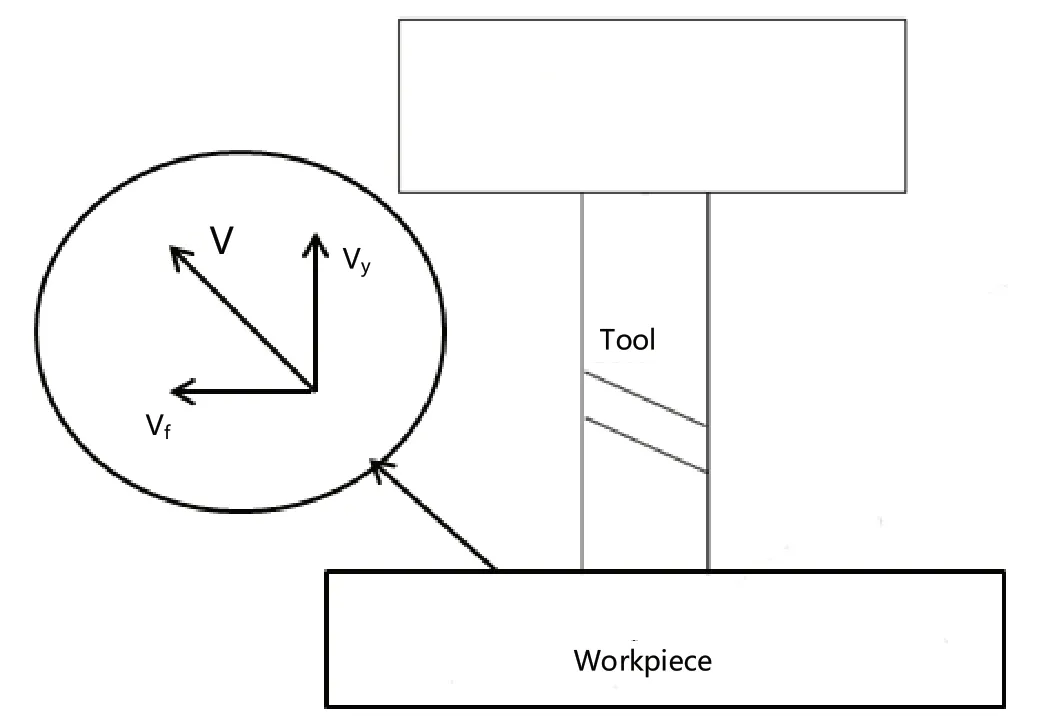
图7 超声振动速度矢量图Fig.7 Vector diagram of ultrasonic vibration velocity

由超声铣削运动学可知，在加工过程中，工件做不衰减的简谐振动，在t 时刻的位移可以表示为如式（23）所示：

t 时刻的振动速度为如式（24）所示：

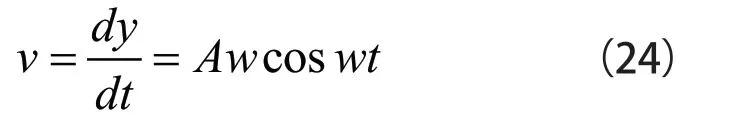
工件对刀具做主运动的速度vf可表示为如式（25）所示：

式中fz-每齿进给量（mm/z）；n-主轴转速（mm/min）；z-齿数；

由振动速度和进给速度可以得到工具在超声振动下的复合速度如式（26）所示：

那么复合后的进给量也发生变化，复合进给量如式（27）所示：

在超声铣削加工下，残留面积的高度H 如式（28）所示：

在超声振动铣削加工下，得到的表面粗糙度理论模型如式（29）所示：

超声铣削加工下表面粗糙度的理论模型的最终公式如式（30）所示：

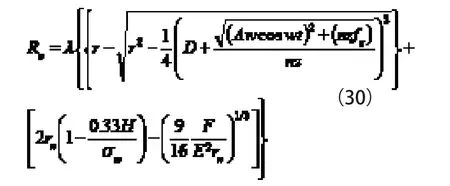
其中式（30）中的λ是单位为1 的比例系数，主要是由机床、变幅杆、刀具材料的刚度和性能决定，可通过试验的拟合来得到具体数值。

由式（22）和式（30）对比可知，当加工参数及刀具参数保持一致时，采用超声振动铣削能够降低表面粗糙度值。

3 结语

综上所述，在工件上施加超声振动，依据超声振动铣削的运动学特性，进行材料的脆-塑性转变条件分析，同时考虑刀具器具相关参数和进给量之间的客观联系，借助物理学等专业领域知识，对铣削工艺加工表面的最大残留高度进行换算，并结合标准阈值进行体系修正，降低数据计算失误的可能性，并基于弹塑性形变的计算工艺等要求，结合高度和弹塑性形变工艺，在特定条件下，精准建立粗糙度计算模型，并根据多方数据进行逆推验算，使超声振动铣削淬硬模具钢表面粗糙度的研究得到简化，提高研究效率。

引用

[1] 曹凤国.超声加工技术[M].北京:化学工业出版社,2005.

[2] 李亮,何宁.高速铣削铝合金时切削力和表面质量影响因素的试验研究[J].工具技术,2002,36(12):16-19.

[3] 刘维伟,李锋,姚倡锋,等.GH4169 高速铣削参数对表面粗糙度影响研究[J].航空制造技术,2012,54(12):87-90+93.

[4] 谭德宁,赵荣荣,齐华英,等.超声波振动车削的设计[J].制造技术与机床,2018(11):58-60.

[5] 李传钰,李金华,姚芳萍.模具钢表面超声辅助激光熔覆Ni60合金涂层的仿真与实验分析[J].制造技术与机床,2022(07):51-57.