基于改进的三层机器学习搜索法极端降雨区域频率估计
2023-02-19左惠强尹建明
杨 哲 杨 昆 吕 娟 左惠强 尹建明
(1.中国再保险(集团)股份有限公司博士后工作站,北京 100033;2.中国水利水电科学研究院,北京 100038;3.水利部防洪抗旱减灾工程技术研究中心,北京 100038;4.中国财产再保险有限责任公司,北京 100033;5.中再巨灾风险管理股份有限公司,重庆 400020)
1 研究背景
受气候变化影响,极端降雨事件日渐频繁,并对现今社会造成严重影响[1-2]。Mondal 等[3]将ENSO(El Niño-Southern Oscillation)指数、全球平均地表气温和印度平均气温作为指标,发现100年回归期的极端降雨频率在局部地区呈上升趋势。Simonovic 等[4]分析了加拿大各地的极端降雨事件的频率和强度,发现中西部地区和东海岸地区存在相反变化趋势。Fernandes等[5]比较了1979—1999年和2000—2015年两个时期巴西的极端降雨事件,在年降雨量和极端降雨的形成机制上都发现显著的变化。Ma等[6]分析了中国东南部632个观测站1969—2013年的日降雨量记录,发现高强度的降雨事件频率在有上升趋势,而中小强度降雨事件频率呈减少趋势。
强度-历时-频率(IDF)曲线用于描述某一站点不同重现期、不同历时的降雨强度量级。站点的频率分析法通常分为两大类:单站点序列分析法,仅用目标站点的历史数据进行IDF曲线的拟合;区域频率分析法,利用相似因子,收集大量拥有相似降雨特征的站点资料,用这些资料进行IDF 曲线的拟合[7]。相比于单站点的频率分析,使用大量样本的区域频率分析法能降低降雨强度估计值的不确定性。在区域频率分析中,收集的与目标站点拥有相似降雨特征的站点的集合被称为同质群体。
同质群体的组建直接影响降雨强度估计值的不确定性。选取的相似因子作为衡量标准,其中包括站点的地理位置特征,或通过其历史气象资料计算得到的年平均降水量、年平均降雨天数等[7-10]。相比于站点的地理位置特征,气象特征更易受气候变化的影响,可以更有效揭示气候变化下不同时期降雨事件频率的变化[11-16]。为考虑在气候变化对不同地点上极端降雨事件频率的影响,以及极端降雨事件的空间差异性,Yang等[17]提出了一种基于机器学习的三层搜索算法,其使用了禁忌搜索法为拥有不同地理和气象特征的目标站点选择出不同的相似性因子,通过这些相似因子进行站点的聚类,进而得到最优的同质群体。为了减少相似因子之间的相关性对站点聚类过程中的影响,三层搜索算法使用拉格朗日乘数法进行。
为进一步降低降雨强度估计值的不确定性,本文从两个方面对现有的三层搜索法进行改进:①提高算法对非线性相似因子中非冗余信息提取的有效性。本文将用特征提取法取代特征加权法进行相似因子间有效信息的提取。②减少同质群体组建过程中对原始输入的依赖。本文将在三层搜索法的框架中添加一种监督站收集技术作为组成同质群体的另一种方法。
2 研究区域和数据
本文选择加拿大不列颠哥伦比亚省作为研究区域。由于靠近海洋和山区,其独特的地理位置使得该地区主要呈太平洋海洋和科迪勒拉山系气候类型,层状降雨将是该地区主要的降雨类型。本文选取了不列颠哥伦比亚省内现有的86 个站点的雨量数据进行试验,其过程所需要的数据如下:
(1)降雨年最大值序列。分别在86个站点上,收集历时分别为5 min、10 min、15 min、30 min、1 h、2 h、6 h和12 h的降雨年最大值序列。这些数据有两个特点:一是时间跨度不统一,最长可达到40 a;二是时间上重复度最高的时段是1985—2004年。
(2)特征因素的提取。从美国国家海洋和大气管理局(NOAA)测绘产品数据库、全球集合预报系统再分析数据产品(GEFS/R)和欧洲中期天气预报中心的全球预报再分析数据产品(ERA-interim)中,在不同的层级高度上提取了1985—2004 年的气象相似因子年序列,其时间分辨率为6 h。提取的相似因子如表1所示。

表1 三层结构中可能的相似因子
3 研究方法
3.1 基于三层机器学习搜索法的极端降雨区域频率估计
3.1.1 区域频率分析法
在区域频率估计法中,假设同质群体内所有站点的降雨序列具有相同的频率分布,则不同回归期的降雨强度估计可用以下指数方程求得[7]:

式中:D表示降雨历时,h;̂T,D是重现期为T年降雨历时为D的降雨强度估计值;是单个站点在降雨历时为D情况下的历史年平均强度值,̂T,D是无量纲的分布函数曲线。其具体实施步骤(图1)如下[7]:
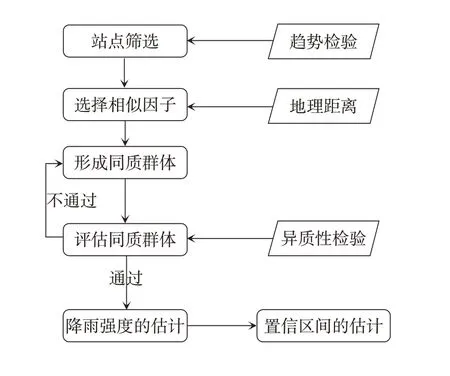
图1 区域频率估计法框架图
(1)站点筛选。通过Pettitt 检验或Mann-Kendall 非参数检验,检查现有站点的降雨年时间序列,选着拥有平稳时间序列的雨量站。
(2)相似因子的选择。在传统的区域频率分析法中,选择相似站点与目标站点的地理距离作为相似因子。
(3)形成同质群体。设定相似因子的上限值,收集范围内特征相似的站点,组成可能的同质群体。
(4)同质群体的评估。对上一步得到的同质群体组进行异质性检验,对不符合同质性标准的同质群体组进行调整,即减少其群体内已有的相似站点,直至满足同质性标准为止。
(5)不同回归期的降雨强度估计。根据步骤(4)得到的同质群体中的降雨序列,识别合适的分布函数,进而估计目标站点不同回归期下的降雨强度。
(6)量化分位点的置信区间。利用同质群体中的降雨序列中得到的线性矩,进行1 000次的参数抽样,模拟对不同降雨强度分位数的置信区间进行估计。
作为整个估计过程中最重要的一步,同质群体的组成直接影响降雨强度分位点估计的不确定性。为了形成更优的同质群体,Yang等提出了一种基于机器学习的三层搜索算法[17]。
3.1.2 基于机器学习的三层搜索算法
三层搜索算法将极端降雨的形成过程分为:行星边界层以外云的形成,城市混合层中降雨的产生,以及城市表层降雨强度受地面影响而变化[17-19]。
第一层:为了区分两种极端降雨诱导云(积雨云或雨层云),选择了对流有效势能指数以及其他在300 hPa 和700 hPa 气压高度之间的气象相关特征为可能的相似因子作为搜索的输入[20-21],以用来确定目标站点上极端降雨诱导云影响的空间范围作为最初的同质群体[17]。此层中最能影响极端降雨云形成的相似因子为对流有效势能。
第二层:在第一层输出的同质群体的基础上,为进一步考虑区域尺度上的气象和地理特征,选取了气压高度在850 hPa以上的气象和地理要素为可能的相似因子作为搜索法的输入,以确定区域尺度上目标站点的同质群体。此层中最能影响区域极端降雨的相似因子为水汽通量散度的垂直积分[20-21]。
第三层:在第二层输出的同质群体的基础上,为考虑城市化效应对降雨的影响,选择能反映城市热岛效应、冠层效应和气溶胶效应相关特征要素为可能的相似因子作为搜索法的输入,进而形成最终的同质群体[13,18,22]。
原始三层搜索法的步骤如图2所示。

图2 原始三层搜索法框架图
(1)相似因子的初选。在第一层中,选着合适的相似性指标作为同质群体形成的衡量标准。
(2)非冗余信息的提取。在选取的相似因子上应用特征权重即拉格朗日乘数法,得到每个相似指标相应权重。
(3)同质群体的形成。采用乘以权重后的相似因子作为衡量标准,使用模糊C 均值聚类法,形成同质群体,并采用区域频率法计算不同分位点对应的置信区间宽度。
(4)得到第一层最优的同质群体及其对应相似因子组合。运用禁忌搜索法,以步骤(3)得出置信区间的宽度为指引,选择下一个可能较优的相似因子组合。重复使用步骤(1)~(3)直至达到预设的搜索次数上限,得到最优的相似因子组合。
(5)得到最终的同质群体。分别在第二、第三层中,重复步骤(1)~(4)。在层与层的衔接中,上一层输出的同质群体会被作为输入的测试区域进人下一层,直至得到最终的同质群体。
本文将针对上述步骤中(2)和(3)中所用到的非冗余信息的提取和形成同质群体所用到的聚类方法进行改进。
3.2 改进的三层搜索法
3.2.1 等距特征映射
作为特征权重法,拉格朗日乘数法适用于线性相关因子之间非冗余信息的提取,但不适用于非线性因子间的信息提取。考虑相似因子之间的非线性相关,为了提高非冗余信息的有效率,本文采用了非线性特征提取方法等距特征映射(ISOMAP)进行因子相关性的处理。
欧式空间并不能较好地描述非线性相关数据点之间的相对关系。在传统的机器学习方法中,数据点之间的距离和映射函数都是定义在欧式空间上的。然而在实际情况中,传统欧式空间的度量难以用于真实世界的非线性数据点,因此需要对数据的空间分布引入新的假设。等距特征映射使用了流形假设,其认为数据点分布在嵌入于外维欧式空间的一个潜在的流形上,或者说这些数据点可以构成这样一个潜在的流形体。
等距特征映射是一种图形演算法,通过使用点之间的最短路径的距离对加权图上的相互关系进行重新构建,在此过程中保留点的原始几何结构[23],其大致做法可总结为:
(1)组建相邻区域。根据目标流形上所有两点之间的距离,通过选择与目标点距离低于设定阈值的数据点或收集特定数目的邻近点组成相邻区域。然后使用加权图G来表示相邻区域之内数据点的关系。
(2)最短路径的计算。基于流形上形成的加权图,计算每个邻域中所有两点之间的最短距离,并将该最短距离用作测地距离形成的距离矩阵

此处采用了Floyd 算法或Dijkstra 算法进行最短路径的计算。
(3)在新维度上构建降维数据。对从获得的距离矩阵使用多维尺度变换法。通过将数据嵌入d维欧氏空间Y,以保持目标流形上原始的几何结构[24]。使用以下等式得到数据在欧氏空间Y下的新分布:

从相关特征中提取的非冗余信息将用作同质群体形成的相似因子。
3.2.2 影响区域法
为了进一步降低降雨强度估计值的不确定性,在改进的三层搜索的框架中,加入影响区域法(ROI)作为另一种形成同质群体的方法。作为一种监督算法,当输入组中有足够数量与目标站点拥有相似降雨特征的站点时,影响区域法通常优于模糊均值聚类法找到最优的同质群体。通过使用相似因子来计算与目标站点的欧几里德距离,并采用异质性估量指标,去衡量该站点是否属于目标站点的同质群体[25-26]。本文使用的异质性度量指标为[27]:
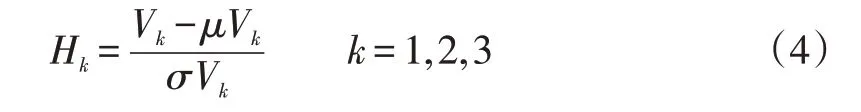
其中
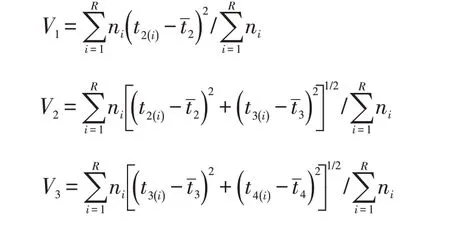
式中:μ为提取序列的均值;Vk为选用的计算指标;σ为提取序列的方差;tˉ2、tˉ3、tˉ4为L-均值(L- mean)、L-变差系数(L-Cv)和L-偏态系数的区域值;t2(i)、t3(i)、t4(i)为单个测站的0 阶、一阶、二阶的线性矩;ni为站点i降雨序列中的样本数目;R代表同质群体中的站点数目。当异质性度量指标Hk小于1 时,此同质群体可认为是均匀同质的,当1<Hk<2 时,此同质群体被认为可能是均匀同质的[7]。
3.2.3 改进的流程
在原始三层搜索法的基础上,加入上述两种方法,得到改进版的三层搜索法框架如图3所示。与原始方法相比,新框架将在以下几个步骤中进行改进:
(1)非冗余信息的提取。用等距特征映射替换原始拉格朗日乘数法,对选择的相似因子进行非冗余信息的提取。
(2)同质群体的形成。影响区域法作为辅助法所形成的同质群体,会与用模糊C 均值聚类法所得的同质群体进行比较,取置信度区间较窄的同质群体为最优。

图3 改进的三层搜索法框架图
4 结果分析
4.1 基础数据分析
根据三层搜索法的层结构描述,各层的相似因子会受到不同时间尺度的气象条件影响。为了更好地描述不同层的降雨相关特征,需要分析各层相似因子不同时间尺度下提取值,以选择最优时间尺度上的特征提取值。
为了选取每层相似因子提取值的最优时间尺度,本文采用每层最能影响降雨过程的相似因子与其他因子的相关系数作为时间尺度的衡量标准。每层因子在不同时间尺度上的提取值通过使用离散小波变换而得到。在第一层,所有站点提取值的相关系数在128 d的时间尺度上达到最高值。这128 d的长时间尺度可被认为是合理的:①虽然降水过程是一个中尺度大气过程,但它可能会受到大尺度现象的影响,包括云的形成、冷暖锋碰撞等。②在三层设计中,第一层中的因子被用作收集在大尺度上具有相似极端降雨相关大气特性的站点。③研究表明,与极端事件相关的大气运动、或对流有效势能相关的特征,都与西非和印度季风的季节性迁移具有强烈的季节性相关性[28-29]。在第二层,对于大多数的站点而言,相关系数在时间尺度为64 d 达到最大值,则64 d 被用作在第二层的时间尺度。在第三层中,由于同质群体的形成主要是依靠24 h的降雨序列作为判断,第三层的特征提取值采用24 h 作为时间尺度。不同时间尺度上的特征值提取值的相关分析只在第一层和第二层中进行。
图4 和图5 显示了各站点相似因子之间的相关系数存在空间差异。尽管在每个站点,其在第一层或第二层的相似因子分别在128 d 或64 d 的时间尺度取得与最能影响降雨过程的相似因子最高的相关系数值,但这些相关值在不同站点上仍存在重大差异。这一结果在另一方面也证明,不同站点上的降雨相似性指标存在空间差异。

图4 第一层不同站点上可能相似因子间的相关系数

图5 第二层不同站点上可能相似因子间的相关系数
4.2 对比分析
在研究区域,本文通过趋势检验法,筛选出75个站点具有平稳序列特征,提取不同时间尺度上的特征值,用其进行同质群体组建,得出以下结论:
(1)模糊聚类法和影响区域法同样有效的。对两种方法得到的在不列颠哥伦比亚省中的75 个雨量站里,49 个站点使用模糊聚类法所得到置信区间会比使用影响区域法得到的要窄。
(2)改进三层搜索算法较原始算法产生更优的同质群体。本文使用区域分位点估计值与真值的均方根误差(RMSE)作为同质群体的比较。此处的真值指用单站点频率估计法得到的不同回归期下的降雨强度分位点。单站点频率估计法通常适用于拥有长序列资料的站点[30]。分别在2 a、5 a、10 a、25 a、50 a 和100 a 的重现期得到对应的区域估计值和单点估计值,最终取这6个回归期的均方根误差的平均值作为判断标准。较优的同质群体会具有较低的均方根误差值。采用同质群体间的对比方法进行均方根误差值的比较,改进算法在研究区域的75 个站点中的63 个站点能产生更优的同质群体。
(3)改进三层搜索算法较传统区域频率分析法产生更优的同质群体。传统的区域频率分析法通常采用距目标站点的地理距离作为收集同质群体的相似指标。此处同样将区域分位点估计值与真值的均方根误差作为同质群体的比较。图6显示了在6个回归期上,分别由改进方法和传统地理方法得出的同质群体的均方根误差值之间的比率。其中由于在改进算法的搜索过程,均方根误差在6个回归期的平均值被作为指引,导致图6中处于低回归期均方根误差比值在1以上,但在其他回归期上改进法所提供的同质群体都会产生较低的均方根误差。
图6 传统区域频率分析法和改进三层搜索法在均方根误差值上的对比(4)改进三层搜索算法较单站点频率分析法提供的结果不确定性更低。此处使用分位点的置信区间宽度作为衡量标准进行比较。对于分位点的置信区间宽度估计,区域频率分析法通过对线性矩的大样本模拟而进行估计,单站点频率分析则假设其置信区间的宽度服从正态分布并使用非参数抽样法进行估计[7]。图7表明,在高回归期,所有台站的置信区间的宽度比中值均低于1,因此改进算法产生的大多数同质群体在6个重现期上产生较低的不确定性,即较窄的置信区间的宽度。
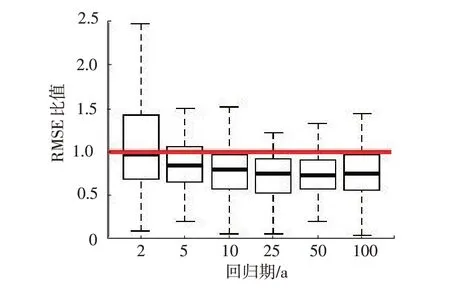
图6 传统区域频率分析法和改进三层搜索法在RMSE值上的对比

图7 原三层搜索法和改进三层搜索法在置信区间宽度上的对比
为了进一步证明改进算法的有效性,本文对75个站点得到的相似因子组合进行了聚类分析,并得到以下结论:
(1)对于第一、二层的75个站点的相似因子组合,聚类分析得到的有效群体数都为2。此结论与前两层改进算法的设计目的一致:在第一层,区分积雨云或雨云引起的极端降雨事件;在第二层,区分对流降雨和层状降雨的目的。
(2)第一、二层中的聚类分析中,各群体中心的相似因子组合之间存在相同因子,如表2所示。对于第一、二层,从宏观和区域尺度上看,相近的地理位置意味着相似的气候特性,进而导致不同群体中云和雨的形成机制存在一定程度的相似性。

表2 第一层、第二层群体中心相似因子组合
5 结 论
考虑到气候变化和城市化的影响,改进的三层搜索算法,能够进一步考虑极端降雨强度在空间上的差异性,形成最优的同质群体,降低降雨强度分位点的不确定性。本文提出了两点改进:①考虑相似因子之间非线性相关性,等距特征映射取代特征加权方法,提取相似因子间的非冗余信息,作为目标站点的降雨相似性指标。②影响区域法作为一种额外的同质群体形成方法,提高同质群体的形成结果。
改进后的版本已经在加拿大的不列颠哥伦比亚省中的两种气候进行了大量的测试。与传统的地理方法相比,改进法提高了同质群体的组成,降低了区域频率估计值的不确定性。但此法的最大弊端在于搜索过程需要大量计算,耗时较长。
