智慧理答,深度学习邀你共舞

徐芳

［摘 要］在数学课堂上，教师的智慧理答不但能激发学生的思考，还能引导学生深度学习。智慧理答，不仅是一种方法，还是对心灵的抚慰、对智慧的启迪、对生命的赏识，能促进师生之间真挚的情感交流，构建一种美好和谐的学习氛围。

［关键词］深度学习；理答；提问

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）35-0065-04

《义务教育数学课程标准（2022年版）》指出，数学教学活动应能引发学生的数学思考，鼓励学生创新。笔者通过调查发现，部分教师在追求课堂活跃度时，忽略了对学生思维能力的培养。简化问题，学生容易找到答案，而学生在出错时，缺乏引导，这难以培养学生深度学习的习惯。数学课堂是动态的，教师的预设不会总是一帆风顺地实行，因此，教师需要锤炼课堂理答语言。精彩有效的理答不仅能激发学生的求知欲，還能为学生指引解决问题的思路，使得学生的思维活跃和情感丰富。

一、遇到“精彩无限”时，激励性理答

在课堂上，当学生的回答达到了教师的期望，教师通常会给予积极的反馈以示鼓励。然而，频繁使用“好”“你真棒”或“你回答得太好了”这类简单的语言，可能会导致学生对这样的表扬无感。真正有激励性的表扬不是空泛的夸奖，它应该能刺激学生进一步思考，并作为一种推动力，引导他们顺利过渡到教学活动的下一阶段。

【案例1】“找因数”练习

师：请找出36的因数。

生1：1，2，4，9，18，24。

生2：1，2，4，3，6，9，12，18，36。

生3：1，36，2，18，3，12，4，9，6。

师：他们都答对了吗？

生4：生1错了，他没找全。

师：认真看一下生2的答案，有什么想说的吗？

生5：如果把4和3的位置调换一下，会更有序。

师：是的，“有序”是数学中的一个重要思想。这么看，生3的答案好像是无序的。

生3：我的答案是有序的，我是一对一对找的，1×36=36，2×18=36，3×12=36……

师：真是个好方法，从1开始按顺序来找，这样就不会遗漏和重复。

教师逐步启发学生思考，并且逐层深入，像剥洋葱一样逐步揭示问题的本质，这不仅培养了学生的逻辑思维，还顾及了学生的自尊。教师恰到好处的理答和不懈追问，将学生的思考引到更深的层次。

二、遇到“浮萍”时，发展性理答

在数学课上经常出现这种场景：学生称自己理解了新学习的知识，但当要求他们阐述概念的原理时，他们往往表现得迟疑不决。这种学习现象犹如浮在水面的浮萍，难以深入水底，说明学生对知识的认知不足。

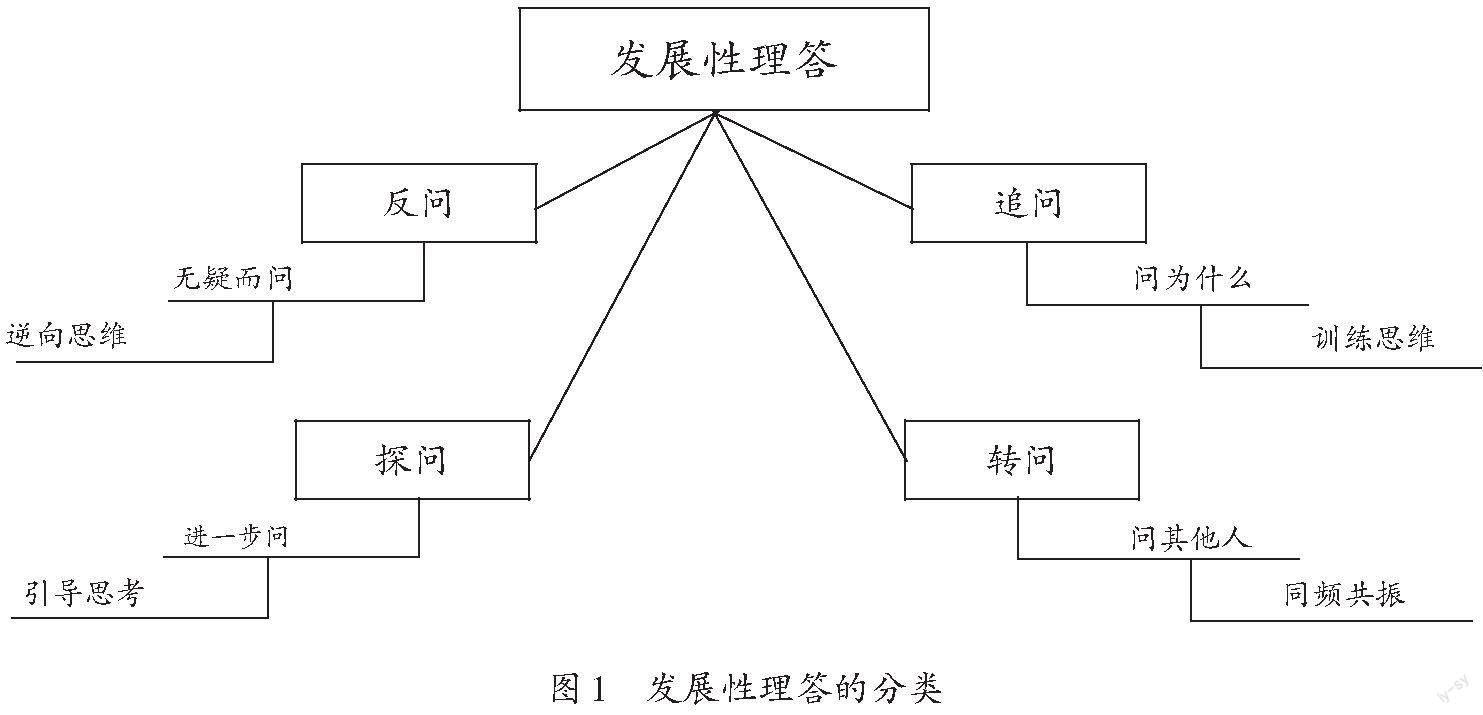
面对这类情况，教师应该保持尊重和鼓励的态度，耐心聆听学生的回答，并运用发展性的答疑方法，即发展性理答中的“四问”技巧来引导学生，旨在通过一系列的引导性问题促进学生深入思考，帮助学生从表层的知识理解迈向深层次的分析和理解。发展性理答主要分为以下几种（如图1）。

1.“反问”逆向思维，质疑认知不足点

通过反问，教师可以巧妙地引导学生去识别并思考他们答案中的不足，这种策略不仅加深了学生对问题的理解，而且激发了他们对知识的深度追问。

【案例2】 “圆的认识”练习

师：一个直径是 6厘米的半圆，它的周长是多少？

生1：3.14×6÷2=9.42（厘米）。

师：半圆的周长是圆周长的一半吗？

生2：不对，还要加上直径。

师：为什么还要加直径？

生3：9.42厘米只是曲线的长，是一个圆周长的一半。

生4：只有封闭图形才有周长。因此，半圆的周长应该是圆周长的一半加上直径。

当学生对半圆周长的理解还停留在表面时，教师进行了反问性理答：“半圆的周长是圆周长的一半吗？”学生开始重新思考问题。经过一番思索，学生意识到“半圆的周长并不是圆的周长的一半”。教师接着引导，学生逐渐明白了半圆由半个圆周和一条直径构成，因此，直径是6厘米的半圆周长应为3.14×6÷2+6=15.42（厘米）。尽管教师的反问实际上是对学生最初回答的否定，但其提问的方式并不直接否定学生，而是促使学生去挖掘知识的深层含义，并引导他们找到正确答案。

2.“追问”思维训练，深入学习达成点

追问就是问为什么，教师根据学生的回答进行“二度提问”。下一个问题比上一个问题更能引发学生深度思考，从而引导学生明白最初问题的理答。追问起到“一石激起千层浪”的作用，激起学生思考的涟漪，点燃学生创新思维的火花，有助于学生深入理解问题。

追问是学生对知识的理解，由肤浅片面到深刻全面，由“知其然”到“知其所以然”的过程。追问是一个寻根究底的过程，它要求教师在听到学生的初步回答后，再次深入地提出更为核心的问题。通过连续追问，每一个新问题都能够比前一个更加促进学生深度思考，帮助他们逐步揭开最初问题背后的深层逻辑。

【案例3】“单循环赛”的问题教学

师：有4名学生参加乒乓球比赛（单循环赛），需要比几场？可以用画图或列表的方式来解决问题。

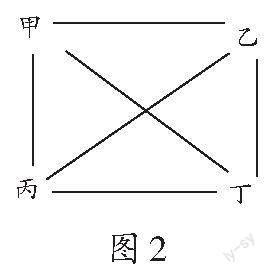
生1（出示图2）：甲、乙、丙、丁代表4名学生，6条线代表比6场。

师：能具体说说是怎样比赛的吗？

生1：甲分别和乙、丙、丁三人各比1场，乙和丙、丁各比1场，丙和丁比1场，一共是6场。

师：很有条理，能把你的话用算式表示出来吗？

生1：可以列加法算式3+2+1。

师：如果是5名学生参加比赛，怎样列算式呢？

生2：再加4场，也就是4+3+2+1。

师：6名呢？

生3：5+4+3+2+1。

师：20名呢？

生4：从19一直加到1。

师：21名、22名呢？

生5：从21加到1；从22加到1。

师：n名呢？

生6：从（n-1）开始，一直加到1。

师：这里的n能表示任何数吗？

生7：不能，它只能表示大于1的整数。

教师通过追问，让学生体验到了“从简单情境寻找规律”的学习策略。当学生展示自己的作品后，教师没有做过多解释，而是把解释权交给学生。在教师的逐步追问下，学生进一步思考比赛场次和参赛人数之间的关系，逐步深化对问题的认识，而不是仅仅停留在表面的记忆和理解上。

因此，在教学中多问“为什么”，有助于学生打开思路，挖掘更深层次的知识结构。有效的追问不仅能够将课堂教学推向高潮，而且能激发学生的好奇心和创新潜能，有助于他們在未来的学习和生活中成为主动的知识探索者。

3.“探问”诱导思考，静思默想重难点

探问是通过多角度、多层次的问题引导，促进学生对知识点进行深入思考。这种策略的运用取决于学生回答问题时的具体表现。如果学生的回答是片面的，教师可以通过探问引导学生从不同的角度重新考虑问题；如果学生在回答时遇到障碍，教师可以巧妙地提供线索，鼓励他们采用新的途径寻找答案。同时，教师也可以逐步引导学生分析问题的每个方面，带领学生层层深入，直到他们对概念和原则有了全面而深刻的理解。

【案例4】“单循环赛”含义的教学

师（出示4名学生进行“掰手腕比赛”的情境）：4名学生进行掰手腕比赛，每2名学生都比1场。共比了几场？

生1：3场。

师：能具体说一说是哪3场吗？

生2：把4名同学分为两组，甲和乙一组，比1场，乙输了，淘汰；丙和丁一组，比1场，丁输了，淘汰；甲和丙又比1场，丙赢了，共比了3场。

师：甲和其他3名同学都比了1场吗？

生3：甲和丁还没比。

师：那就是比4场了？

生4：也不是4场，还有乙和丙、乙和丁，因为比赛规则是每2名学生要比1场，所以不论输赢都要继续比下去。

师：“输了就淘汰，赢了就继续下场比赛”的比赛叫淘汰赛。能具体说说什么叫淘汰赛，什么叫单循环赛吗？

生5：淘汰赛就是比1场淘汰1名学生，比到只剩1名学生为止。而单循环赛就是，不论输赢，每2名学生都要比1场。

一开始学生认为比赛次数是3场，原因可能是没有读懂“每2名学生都比1场”的比赛规则。当学生出现错误时，教师没有立即进行评价，而是采取探问的方式——能说一说是哪3场吗？学生在第一次自我解释后仍未意识到错误，教师继续以新的问题使学生进一步思考——甲和其他3名同学都比了1场吗？最后，学生深刻理解了单循环赛和淘汰赛的不同，突破了本节教学的重难点。

探问法的优点在于它能激发学生思考，引导他们从不确定性中提出问题。这种持续的思维训练帮助学生形成了深度思考的习惯，不断拓展他们的知识边界。

4.“转问”同频共振，夯实知识生长点

转问，是指当学生回答卡壳或回答不正确时，教师不代学生回答，而是将问题抛向另一个学生，或是让学生自己转问同伴，使问题得到解决的理答。转问可以让更多学生参与讨论，也可以了解学生对问题的掌握程度与不同看法。

这样做的目的是促进学生间的互动和交流，深化他们对问题的理解，达到“山重水复疑无路，柳暗花明又一村”的教学效果。

【案例5】“轴对称图形”教学

师：什么是轴对称图形？

生1：一个图形的两边都是一样的，就是轴对称图形。

师：你们的想法都一样吗？

生2（举起一个平行四边形）：这个图形两边也一样，可是它不是轴对称图形。

生3：平行四边形不是轴对称图形，它对折后两边不一样。

师：怎么修改生1的话才能使其正确呢？

生4：对折后，两边都一样的，就是轴对称图形。

生5（拿出一张长方形纸片）：对折后，两边都完全重合，就是轴对称图形。

师：再说完整一些。

生6：一个图形对折后，两边都完全重合，就是轴对称图形。

生1是理解轴对称图形含义的，但表达时不够严密。此时，教师采用了转问的理答方式“你们的想法都一样吗？”，使学生产生了疑惑。接着，教师转问“怎么修改生1的话才能使其正确呢？”，学生在思考后，得出了较完整的答案，对轴对称图形的理解也加深了。

如果教师仅仅因为急于听到自己想要的答案而忽视学生的思考过程，那么有可能不慎伤害到学生的自信心，降低他们参与课堂讨论的热情。这样的做法不仅不能有效利用错误作为教学资源，而且也缺乏对学生认知过程的关注，没有为学生提供足够的思考和理解的空间。恰当的智慧转问不是为了逃避问题，而是为了激发学生的思维碰撞和知识分享。这种策略鼓励学生通过讨论和探索找到问题的答案。在这个过程中，学生的理解会因为不同的视角和解释而得到巩固和拓展。

三、遇到“事故”时，针对性理答

在教学过程中，教师的预设固然重要，但应对课堂上的即时情况与学生的个体差异同样关键。对于一个活跃的课堂来说，学生的错误并非意外，而是像在精心编排的乐章中出现了意外的音符，一个有经验的教师会知道如何利用这些偶发的“不和谐”来丰富整体的教学旋律。

以“三角形内角和”的教学为例，一位年轻教师创设了一个辩论环节：钝角三角形、锐角三角形、直角三角形谁的内角和大？结果多数学生都说一样大，但有一名男生认为钝角三角形的内角和大。可能是因为这位学生的发言和教师预设的下一个环节不一致，结果教师一句话带过，没有给男生解释的机会。男生的错误观点实际上提供了一个教学的切入点。如果教师能够当场鼓励他展示自己的“证明”，不仅能激发他的参与热情，也能让其他学生意识到错误是探索知识和深化理解的一部分。通过询问“为什么？”并邀请学生证明他们的观点，就能提供一个让全班学生参与学习的机会，使学生能够在公共场合进行思考、交流和辩证。

教师应当倾听学生的想法，了解他们的生活经验和思维方式，从而深入挖掘每个错误背后的认知机制。有时，学生的错误是因为他们的思路和教师的不同，或者是他们的认知过程中只差了最后一块拼图。通过细致的分析，教师可以发现学生的错误是接近正确答案的，并且可以设计针对性的策略来引导学生找到正确的思维路径。

个性化的答疑和针对性的理答能够确保课堂教学不是一个单向的信息传递过程。这种对话式的教学更能激发学生的学习潜力，让他们在探索和发现的过程中找到学习的乐趣。

四、遇到“冷场”时，目标性理答

在教学过程中，遭遇课堂“冷场”是一种常见挑战。当教师期待着互动却遇到一片沉默时，这不仅意味着学生可能没有跟上节奏，也可能是教学设计与学生的认知水平脱节。

【案例6】“复式折线统计图”导入教学

师：有这样一句话——早穿棉袄午穿纱，围着火炉吃西瓜。大家有没有听过？

生（齐）：没有。

师：那我给大家解释一下。“早穿棉袄”是早晨穿上棉袄，“午穿纱”是中午穿上很薄的衣裳。“围着火炉吃西瓜”这句话想表达什么？

（学生很是茫然，不再说话）

课后，教师和学生交流时才知道“早穿棉袄午穿纱，围着火炉吃西瓜”这样的场景离学生的生活太远，学生没有这样的生活体验，因此无法理解这句话的含义，即使教师解释了，学生依然不明白这句话的意思。也就是说，教师没弄清楚学生困惑的原因，不能运用理答策略激活学生的思维。

【案例7】“乘法”教学

师：一辆52型拖拉机一天耕地150亩，12天耕地多少亩？

生1：52×150×12。

师：你为什么这么列式？

生1：我写错了。

师：你认为正确的该怎么列式？

（生1沉默了）

师：能采用乘法计算，说明你是有想法的。那如果你每天吃2个粽子，5天吃几个？

生1：10个。

师：能说一说你的思路吗？

生1：每天2个，5天就是5个2，5×2=10。

师：如果1个粽子3元，你每天吃2个粽子，5天吃几个？

生1：还是10个。

师：“3元”这个条件你怎么没用到？

生1：这个条件是多余的。

上述案例中的问题情境属于有条件干扰的生活问题情境。学生对52型拖拉机比较陌生，不能从情境中提取有用的数学信息。教师根据这种情况，采取了再组织的理答方式，学生很容易就解决了问题。

当课堂上出现“冷场”现象时，教师要运用自己的教育智慧，迅速找出问题所在，进行巧妙理答，可以采取引答的方式，也可以将一个大的重点问题化解为一系列小问题，逐一进行探问，提供回答线索，或者利用幽默、鼓励的语言，化解尴尬场面，激活学生思维。

综上，理答是一门艺术，智慧理答能帮助学生走向深度学习，能引领学生走出理解误区，进行深入思考，给课堂带来精彩而有效的生成性资源。总之，理答必须“答”在“点”上，从索案型理答走向索思型理答；从关注个体学生走向关注全体学生；从关注学生的学习结果走向关注学生的思考過程。