基于RVM-GRNN组合模型的天然气负荷预测研究

邵必林，刘 通，饶 媛

（西安建筑科技大学 管理学院，陕西 西安 710055）

0 引言

随着中国城市化进程加快，我国能源面临匮乏问题，环境与资源代价高昂。煤炭、石油等传统能源一方面因过度开采而储存量越来越少，另一方面也给环境带来了巨大污染，因此发展低碳经济、开发清洁能源、减少大气排放成为长远发展的必然要求。天然气作为一种清洁能源，因其排放的温室气体较低，并且没有硫化物等污染物排放而逐渐受到关注。2020 年，我国天然气产量为1 925 亿立方米，同比增长9.8%，天然气探明新增地质储量1.29 万亿立方米，我国天然气能源储量丰富。但是随着天然气使用的逐渐普及，许多城市已出现天然气供求矛盾，“气荒”问题日益严重。因此，合理把握天然气用户用气规律，分析影响用户需求的各种因素，对天然气负荷值进行预测是当前亟待解决的问题。

通过对国内外文献进行梳理发现，现有天然气负荷预测模型主要分为单一模型和组合预测模型两种。单一模型的天然气负荷预测主要分为两个阶段，第一阶段主要是通过传统数理统计、相关性分析和回归分析进行预测分析。Sarak等［1］将度日法应用于天然气负荷预测，将城市的度日、人口和居民分布记录用来估计全国范围的天然气需求，结果表明，该种方法能够定位能源需求分布。Ding［2］设计一种自适应灰色预测模型，对比于传统灰色模型，改进模型的拟合性能和预测性能优于原始模型。Ying 等［3］在自回归模型中加入外生变量，提高了模型计算效率。第二阶段是在人工智能、大数据、机器学习背景下，使用群智能算法、机器学习算法等进行预测分析。2012 年，Demirel［4］运用多元回归模型、ARMAX 模型和BP 神经网络对天然气负荷进行预测，通过预测结果比较发现，相较于ARMAX 和多元线性模型而言，BP 神经网络预测效果更好。Kodogiannis 等［5］用乘法小波神经网络代替模糊规则的THEN 部分，提出一种新型的神经网络模型，通过与传统神经网络相比，本文提出的负荷预测模型具有更高的准确性。Szoplik［6］、Laib［7］、Taspinar［8］对多层神经网络进行设计和训练，比较了使用多层神经网络模型在隐层神经元数量和训练过程中使用的数据集大小方面的预测结果，实验证明，该模型可用于任何情况。郭琳［9］对比分析了LSTM 模型、GM 模型、SVM 模型和BP 神经网络对燃气负荷预测的效果，结果证明LSTM 模型在燃气负荷预测领域优于其他3 个模型。王晨［10］对比分析了PCA-WNN 模型与BP 神经网络、灰色预测模型、广义回归模型预测效果，最终确定PCA-WNN 模型在精确性和运算速度上具有优势。舒漫［11］建立基于XGBoost 算法的成都市城市燃气日负荷及季度负荷预测模型，首次将XGBoost 算法应用于燃气负荷领域。何恒根［12］针对BP 神经网络预测时间长的缺点，采用主成分分析法进行数据降维，减少BP 神经网络预测时间。黄维［13］在深度信念神经网络中添加了自适应学习率，补足了传统的DBN 在预训练和调优过程中注重调节w和b的值，忽视学习率的缺点。

组合预测法一般分为横向和纵向两种：横向是将数据分解，使用不同的方法分别预测，最后相加；纵向是将前一种模型的预测结果当作数据集，输入后面的模型进行训练和预测。组合模型法可以将多种模型的优点集合起来，缺点是预测时间长、模型建立复杂度高。Sánchez-úbeda等［14］提出一种分解组合模型，该方法结合了预测模型的简单表示，使专家能够综合判断分析和统计预测调整情况，具有较高的计算效率和准确性。Forouzanfar 等［15］将Logistic 方法与自然语言处理和遗传算法结合，实验结果证明了Logistic 函数可以应用于天然气预测领域。Liu 等［16］提出一种基于多小波变换和多神经网络的短期负荷预测方法。仿真结果表明，组合的负荷预测模型精度高于任何一个单一的网络模型和未经多小波变换预处理的3 种神经网络组合预测模型。Zhu 等［17］提出一种基于SVR 的支持向量回归局部预测方法和FNF-SVRLP 局部预测方法，对天然气短期需求进行预测，与单一模型相比，该模型具有更高的预测精度。Zhang［18］提出一种贝叶斯模型平均组合预测天然气消费量的方法，其能够有效地处理模型结构和参数的不确定性，提高预测精度。Wang 等［19］将非线性模型与线性模型相结合，建立了自回归综合移动平均模型，有效地融合了线性模型和非线性模型的优点，提高了预测性能。刘媛华［20］将BP 神经网络和SVR 两种方法加以组合并对空气质量指数进行预测，实验证明，该模型泛化能力更强。朱青等［21］将LSTM 和XGBoost 两种模型进行组合，实验结果表明组合模型的RMSE 低于3种单一模型。

以上方法没有考虑不同阶段的天然气负荷值变化规律，以及未提出精确度更高的预测模型。针对该问题，本文采用RVM 模型与GRNN 模型组合的形式进行不同阶段的天然气负荷预测。相关向量机模型（RVM）对天然气负荷数据线性部分具有良好的分析能力。广义回归神经网络（GRNN）能够很好地适应非线性映射，具有不容易过拟合、泛化错误率低、结果易解释的优势。

1 相关理论基础

1.1 RVM模型

相关向量机（Relevance Vector Machine，RVM）是由Tipping［22］在2001 年提出的机器学习算法，该模型基于贝叶斯框架指导，保留相关向量点。贝叶斯理论是在先验概率约束条件下，经过自身相关运算去除没有关系的点，最后获得一个稀疏化模型。相关向量机模型在对数据进行训练预测的过程中，许多参数的后验概率值会逐渐接近于零，而这些数据实际上与天然气负荷预测没有关系，仅有较少数量的数据点即相关向量参数的后验概率非零，对模型预测起关键作用，原理如式（1）所示。其中，z为目标变量，x为输入数据，λ为权值，θ为数据噪声精度，值为σ-2。

其中，y(x)为均值，由线性模型给出，模型如式（2）所示。其中，k(x，xn)为核函数，b为偏置参数。

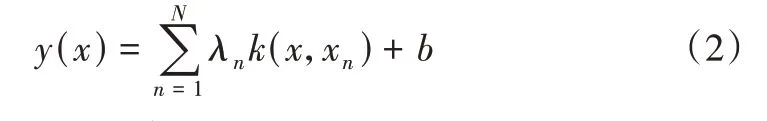
在相关向量机中，若对输入向量进行N 次检测，与之对应的目标值为z=(z1，z2，…zN)T，其似然函数为如（3）所示。

对零均值以下的高斯先验而言，由于线性模型与相关向量机的先验概率部分相似，故需加以考虑，权参数向量λ先验函数如式（4）：

式（4）中，αi是参数λi的精度值，超参矩阵为α=(α1，α2，…，αM)T。通常需对α进行赋值，这也意味着每个参数精度的初始值相同。超参数矩阵与相对应的权参数后验概率值成反比关系，即超参数矩阵增大时，后验概率值便会不断减小，当其后验概率越小，与它有关的函数预测作用率也越低，需将其删掉，因而新的概率检验模型会呈现出稀疏化的形式。

经过实验发现，将相关向量机模型与线性模型结合，其权值参数后验概率分布仍符合高斯分布，结果如式（5）所示。其中，μ为均值，∑为方差。

对于α、θ的最优值，可以使用第二类最大似然方法进行确定。该方法是将边缘似然函数进行最大化得到，边缘似然最大化如式（6）所示，其中，z=(z1，z2，…zN)T。

通过对上式进行对数求导可实现目标最大化，从而求出超参数α、θ最优解，求解结果如式（7）所示。其中，μi为均值μ的第i个向量分量，δi=1 -为协方差矩阵对应的第i个元素。

1.2 GRNN模型

广义回归神经网络（General Regresion Neural Network，GRNN）是由Specht［23］于1991 年提出的一种新型网络结构。对比于传统神经网络，广义回归神经网络采用最大概率原则计算神经网络输出，因此该网络具有很强的非线性映射能力，对非线性数据的预测优于一般径向基函数，在样本较多或较少时都具有很好的学习能力。

广义回归神经网络结构有输入层、模式层、求和层和输出层4 种，其计算逻辑如式（8）所示。其中，X是训练集的输入向量；Xi为训练集中第i个样本，Xi=表示当前样本X与Xi间的欧式距离平方。

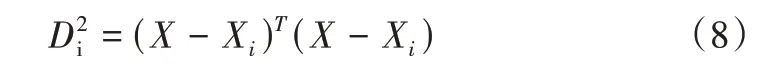
模式层中，第i个神经元的输出为X与Xi之间欧式距离平方的指数形式，如式（9）所示，其中，σ为平滑因子。

求和层由两部分组成。其中，第一部分与输出向量维数m对应，共有个j=1，2，…，m节点。第j个节点输出Sj为网络训练集中第i=1，2，…，N个样本的输出向量Yi=[yi1，yi2，…yim，]T中的第j个元素yij与模式层第i个神经元输出Pi的加权和（以yij当作模式层中第i个神经元Pi与求和层中第j个神经元间的连接权值），其计算式如式（10）所示。

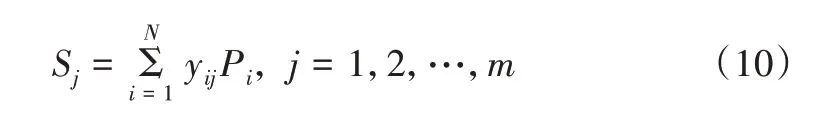
求和层第二部分只有1 个节点，输出SD为模式层各节点输出Pi之和（作为输出层各节点计算的公共分母项），其计算式如式（11）所示。

输出层神经元个数与输入向量Y维数m相同，各神经元的输出为求和层中两种求和结果相除，如式（12）所示。

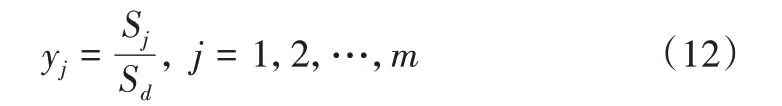
因此，对于广义回归神经网络参数，确定平滑因子σ的值是最重要的工作。

2 基于RVM-GRNN的天然气负荷预测模型

2.1 影响因素选取

在天然气负荷的诸多影响因素中，气象条件是影响其变化的重要因素，主要包含温度、天气类型、湿度、降雨量等。温度是导致气象敏感负荷变化的主要因素，温度一般分为日最高温度、最低温度和平均温度。温度一般与天然气负荷值呈现负相关关系，特别是对于居民用气而言，当温度较低时，取暖用气以及外出减少、室内活动的增加都会导致天然气使用量的增大。而天气类型的变化也会影响人们的出行，进而影响天然气的使用，比如当天气类型为晴天时，人们一般会外出，因此天然气使用量较少，当天气比较恶劣时，人们会选择在家里，天然气使用量较大。此外，还有节假日、突发性事件、商业活动、供热取暖用气等因素也对天然气负荷值有一定影响。但是过多的影响因素会导致预测模型构建复杂、预测时间过长。通过对天然气负荷影响因素进行皮尔逊相关性分析，然后剔除掉影响因子低的因素，留下相关性高的影响因素用于训练，这样既可以减少预测时间，还可以提高预测精度。皮尔逊相关性计算公式如式（13）所示。其中，Rxy表示变量x与变量y的相关性值；n为变量x、y观测值的数量；xi表示变量x的第i个观测值，yi表示变量y的第i个观测值；表示变量x的平均值，表示变量y的平均值。

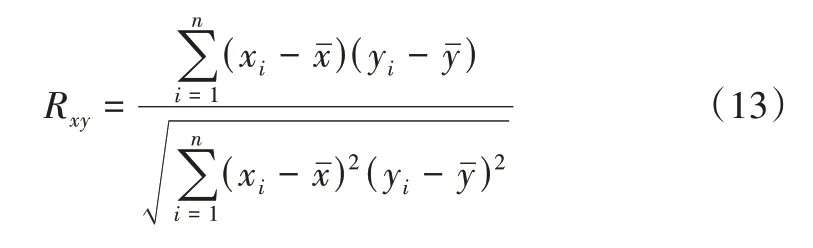
经过皮尔逊相关系数法分析，各影响因素与天然气负荷值的相关系数值如表1 所示。当皮尔逊相关系数绝对值小于0.1 时，判断为影响因素与天然气负荷值相关性不强，因此本文最终选定影响因素为最高温度、最低温度、历史负荷值、风力值。此外，近年来西安市供热能源中天然气所占比例越来越高，西安市集中供热时间为11 月15 日至次年的3 月15 日。因此，本文将天然气负荷预测分为两部分，分别为非供热阶段预测和集中供热阶段预测。

Table 1 Pearson coefficient value of natural gas load influencing factors表1 天然气负荷影响因素皮尔逊系数值

2.2 数据处理

天然气负荷值数据样本的质量和数量会对预测模型的效果产生很大影响。由于数据在采集过程中会出现各种各样的问题，本文使用的数据处理方法主要有3 种：缺失数据补齐、异常数据修正和数据归一化。缺失数据补齐主要是依靠样本之间的相关性修补数据，根据具体变量的实际分布情况采用平均值、众数、中位数进行修补。异常数据主要是受到一定随机因素和潜在波动的影响，因此天然气负荷值的走势会不同于之前的数据点，对整体负荷序列发展趋势产生干扰，不利于预测。针对连续突变的异常情况，可以历史相同日期的正常数据取平均值。未进行归一化时，由于特征向量中不同特征值的差异很大，会导致预测模型训练过程中梯度下降方向容易偏离，从而增加了训练时间并且拟合效果较差。进行归一化后，数据评价标准统一，避免了小数据值被大数据值吞食。梯度在下降过程中更为平顺，会使网络快速收敛，更快寻找到目标函数的极小值。目前，常见的归一化方法有Z-score 分数法、最大最小归一化方法。本文采用最大最小归一化方法，将原始数据规范到［0，1］区间，其公式如式（14）所示。其中，X为原始天然气负荷值数据，Xmax、Xmin分别为原始负荷值数据的最大值和最小值，Xnorm为归一化后的数据。

2.3 RVM-GRNN天然气负荷预测模型

天然气负荷数据具有非平稳、周期性波动特点，RVM和GRNN 组合模型能够拟合数据中线性部分和非线性部分。天然气负荷数据中线性部分由RVM 模型进行拟合。GRNN 模型则是拟合RVM 模型残差中的非线性部分。

令Rt为RVM 模型t 时刻的预测结果，Zt为天然气实际值，gt为t时刻实际值与RVM 模型预测结果的差值，表示为gt=Zt-Rt。{gt}为RVM 模型所有预测差值的集合。{gt}用GRNN 模型进行逼近，其预测结果设为Gt，则组合时间序列预测模型结果如式（15）所示。

RVM-GRNN 天然气负荷预测模型结构如图1所示。

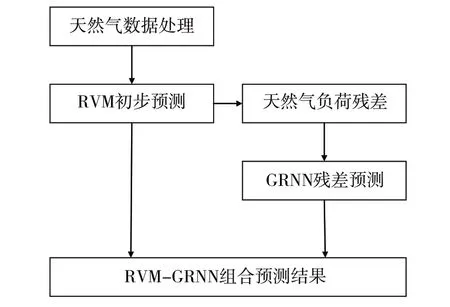
Fig.1 RVM-GRNN model structure图1 RVM-GRNN模型结构

具体建模步骤为：①对天然气负荷值数据进行预处理，修补缺失值和异常值，并对数据归一化；②构建RVM天然气负荷预测模型，输入训练集，得到预测结果Rt；③使用实际值Zt减去Rt得到残差gt；④构建GRNN 残差预测模型，将残差gt导入训练好的GRNN 模型中，进行残差预测，得到预测结果Gt；⑤将步骤②所得Rt和步骤④所得Gt相加则为RVM-GRNN 模型的预测结果。

2.4 模型检验

为检验各模型对天然气负荷预测效果，本文选用平均绝对误差（MAE）、均方误差（MSE）及平均绝对误差百分比（MAPE）3 个指标，计算公式如式（16）—式（18）所示。其中，n 为样本数量，Zt为天然气负荷实际值，为天然气负荷预测值。

3 实例分析

3.1 数据来源

考虑数据完整性和可得性，以西安市某气站2010-2015 年每日天然气负荷值为算例，收集天然气负荷值数据1 826 条，负荷值单位为万m3/日。根据西安市集中供热时间段将数据集划分为非供热阶段和集中供热阶段，其中，非供热阶段数据1 220条，集中供热阶段数据606条。

3.2 比较方法设置

为显示本文所提组合模型效果，选用天然气负荷领域预测常用方法BP 神经网络（Back Propagation Neural Network，BPNN）、多元线性回归（Multivariable Linear Regression model，MLR）和 极 限 学 习 机（Extreme Learning Machine，ELM）进行比较。BPNN 模型是通过输入变量对预测值进行拟合，通过赋予输入向量不同的权重，这种层次结构的正向传播过程可以得到预测误差，之后再利用反向传播法得到各层参数的梯度，根据梯度下降法更新参数，重复这种训练过程使得预测误差最小化。MLR 模型在训练阶段计算出天然气负荷值与影响因素之间的回归系数，再将需要进行预测时间段的相关数据输入，得出预测值。ELM 模型具有良好的泛化性能，比起传统神经网络模型，其训练过程简单、输入权值和阈值随机获得、计算量小，已广泛应用于各种预测领域。

3.3 模型预测效果

3.3.1 RVM与GRNN模型参数设置

相关向量机的预测效果受到核函数选择和核参数设置影响，对常用核函数进行对比分析发现，使用柯西核函数预测效果更好，同时使用控制变量法确定核参数，最终确定核宽度为5，迭代次数为30。GRNN 模型参数主要是平滑因子，本文对平滑因子使用交叉验证的方式进行确定，最终设置为0.1。完成参数设置后，将本文提出的RVM-GRNN 组合模型、RVM 模型及GRNN 模型进行对比，验证组合模型天然气负荷预测的有效性。

3.3.2 非供热阶段天然气负荷预测

非供热阶段天然气负荷预测使用900条数据作为模型训练集，100 条数据作为测试集。最终预测结果及评价指标如图2和表2所示。

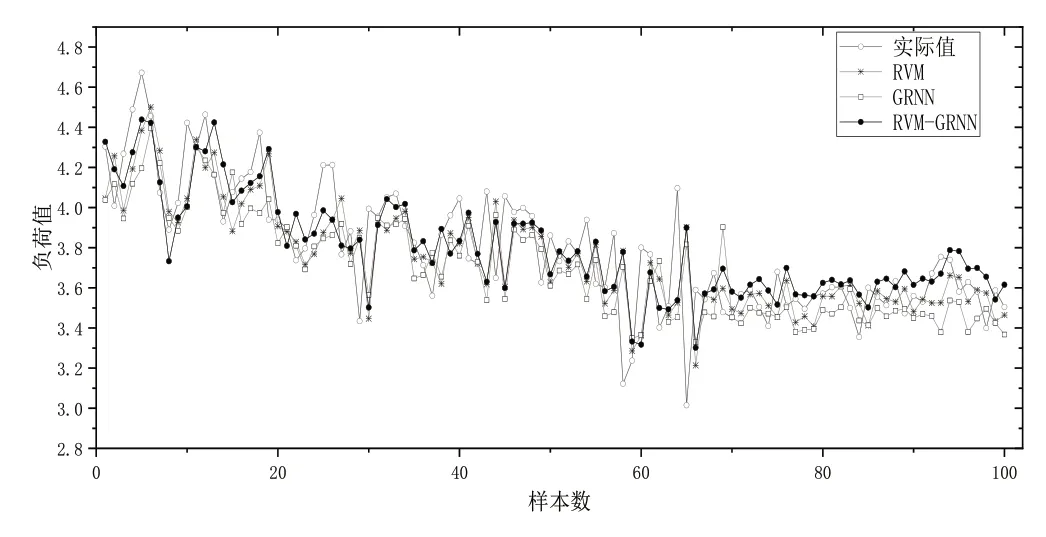
Fig.2 Comparison of prediction results of various models of natural gas load in non-heating stage图2 非供热阶段天然气负荷各模型预测结果比较

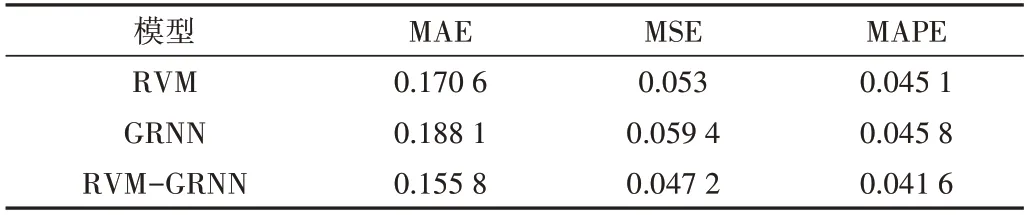
Table 2 Comparison of prediction and evaluation indexes of three models in non-heating stage表2 非供热阶段3种模型的预测评价指标比较

由图2 可知，3 种模型的预测走势与天然气负荷实际值大致相同，但是RVM-GRNN 组合模型比起单一的RVM和GRNN 模型而言，RVM-GRNN 组合模型的天然气负荷预测效果更优。为了对预测结果作进一步分析，本文使用MAE、MSE、MAPE 3 种评价指标进行判断，从表2 可以看出，组合模型的MAE、MSE、MAPE 值均小于RVM 和GRNN模型，由此可以断定RVM-GRNN 组合模型的预测效果更优。

为了验证本文RVM-GRNN 组合模型的有效性，与传统常用天然气负荷预测模型进行比较。图3 为传统天然气负荷预测模型与组合模型的误差曲线比较，可以看出，组合学习方法的误差分布点在零附近波动，表明其误差较小，而传统天然气负荷预测模型误差分布波动较大。

Fig.3 Error comparison of prediction models in non-heating stage图3 非供热阶段各预测模型误差比较

从表3 可以看出，传统模型的评价指标均大于组合模型，进一步证实了组合模型的适用性，预测效果优于传统模型。

Table 3 Comparison of evaluation indexes of traditional prediction models in non-heating stage表3 非供热阶段传统预测模型评价指标比较

3.3.3 集中供热阶段天然气负荷预测

集中供热阶段天然气负荷预测使用500条数据作为模型训练集，100 条数据作为测试集，其预测结果及评价指标如图4和表4所示。

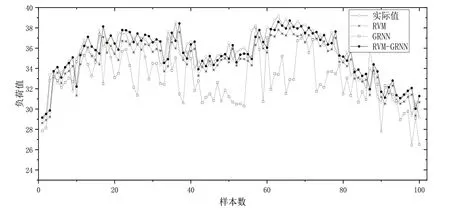
Fig.4 Comparison of prediction results of various models of natural gas load in heating stage图4 供热阶段天然气负荷各模型预测结果比较

由图4 可以看出，在集中供热阶段，天然气负荷值波动幅度较大，3 种模型中，GRNN 模型预测效果相对较差，有多个数据点的预测值偏差较大，RVM 模型和RVMGRNN 组合模型预测效果较好，预测结果与负荷值走势相同。从表4 评价指标可以看出，RVM-GRNN 组合模型的MAE、MSE、MAPE 均小于RVM 和GRNN 模型，因而对于供热阶段而言，组合模型优于单一模型，也表明RVM-GRNN组合模型在供热阶段天然气负荷预测也具有适用性。

Table 4 Comparison of prediction and evaluation indexes of three models in heating stage表4 供热阶段3种模型的预测评价指标比较

集中供热阶段组合模型与传统预测模型的误差结果比较如图5 所示。结果显示，传统模型预测误差波动较大，组合模型预测误差相对较小。

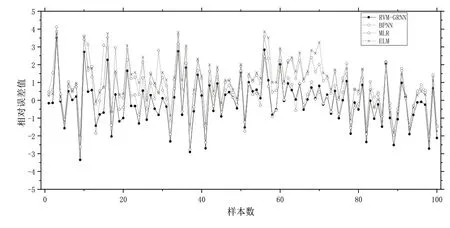
Fig.5 Error comparison of prediction models in heating stage图5 供热阶段各预测模型误差比较

从表5 也可以看出，组合模型的评价指标均小于其他模型，表明在集中供热阶段，组合模型的预测效果依然优于传统天然气负荷预测模型。

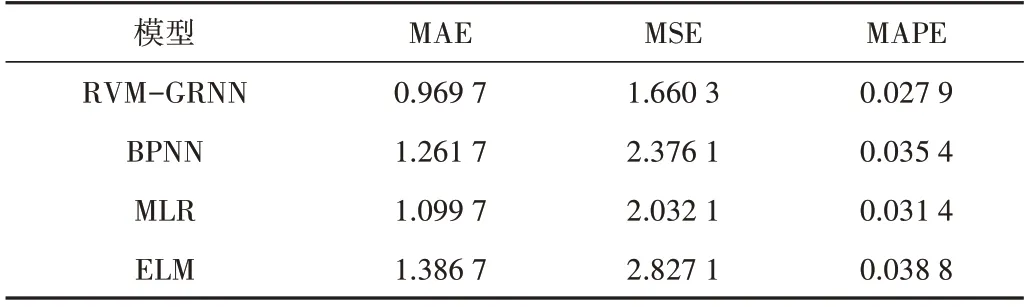
Table 5 Comparison of prediction error indexes of three models in heating stage表5 供热阶段传统预测模型的评价指标比较

4 结语

本文在现有天然气负荷预测研究成果的基础上，分析了西安市天然气负荷量在非供热阶段和供热阶段的特征，并利用RVM 和GRNN 组合预测的优化方式，拟合天然气负荷值的线性和非线性特征。通过与单一模型预测效果进行比较，非供热阶段组合模型的MAPE 比RVM 模型降低7.76%，比GRNN 模型降低16.13%。集中供热阶段组合模型的MAPE 比RVM 模型降低10.29%，比GRNN 模型降低73%。为进一步验证模型适用性，对组合模型和传统预测模型预测结果进行比较。数据表明，RVM-GRNN 组合模型预测效果更好，不论是在非供热阶段还是集中供热阶段，组合模型都可以对天然气负荷值进行准确预测，可以为供气公司供气提供指导。但是影响天然气负荷的影响因素众多，本文仅考虑了供热、温度、历史负荷和风力等因素。对于天然气使用而言，还受政策、商业活动、人口流入流出等多种因素影响。因此，后续研究可以考虑引入更多因素，以提高天然气负荷预测准确性。