“力的分解”依据及有效教学探讨
2023-02-17杨端方
杨端方 陈 刚
(1.遵义市第四中学,贵州 遵义 563006;2.华东师范大学教师教育学院,上海 200062)
1 问题的提出
“力的分解”承接“力的合成”,是高中力学的重要基础.不同版本的教材对于“力的分解”依据侧重点不同,人教版强调“问题解决需要”,教科版、沪教版、粤教版、鲁科版等均强调“力的作用效果”,因而存在一定疑问:到底按照“力的实际作用效果分解力”还是按照“解决问题需要分解力”进行教学比较合理呢?学生也会疑问:在具体问题情境中应该怎样分解力?为什么要这样分解?笔者认为,存在上述疑问的原因是教师在教学过程中单一强调某一个分解依据、对于“力的分解”实质不清晰等.
基于此,本文首先将对现有的两种分解依据进行讨论,然后通过一个具体的例子,讨论“力的分解”实质是什么,“力的分解”教学实质是什么,最后给出“力的分解”一节的教学建议.
2 关于“力的分解”存在的两种提法以及各自的不足
2.1 “力的分解”按力的作用效果分解
目前,“力的分解”一节内容中,很多版本教材都强调“力的分解”应该按力的“作用效果”.在实际教学中,常常基于一个实验(常见几种实验模型如图1),直接引导学生寻找力的作用效果来确定分力的方向,接着引入真实情景构建模型,利用平行四边形定则求解分力大小.[1]这使得“力的分解”处于“有情景而无问题”的状态,有种“为了分解而分解”的意味.经历上述过程,学生不知道为什么要分解、为什么这样分解;此外,每一个实例都只是提供一个情景,分解也只是一种方式,容易产生特定情景中下的唯一分解方式.如对于斜面上的物体模型,如果只给学生演示图1(b)的情况,学生在遇到图1(d)以及刨子的挠斜面模型(如图2)等这两种情况时,还可能按照图1(b)中的分解方式.

图2 刨子的挠斜面模型
2.2 “力的分解”按实际问题需要分解
人教版一直都强调“力的分解”应按问题解决需要”,例如2010年版教材中,从力的合成角度分析耙的运动情况,表述为“为了分析和解决问题”.[2]于是,部分教师将视角转为了“按实际解决问题需要进行分解”,基本不提“按力的作用效果进行分解”.而合力与分力的概念本身就是在“等效”的基础上建立的,无论是“力的合成”还是“力的分解”,都无法避开“作用效果”.此外,具体力所产生的效果(挤压、拉伸或运动状态改变等)是物理问题产生的前提条件,如果没有物理效应,就不会想要研究导致这些效果产生的具体某个力的大小和方向,即不会产生物理问题,分解也就没有任何意义.如果脱离具体问题情境,单纯按“问题解决”分解,而不提力的“作用效果”,学生不仅会疑惑于分解背后的物理依据和物理意义体现在哪,还会在分解力时缺少具体的标准和抓手.
3 “力的分解”的实质
一个特定的物理问题,如果可以用“力的合成”方法来解决,也一定可以用“力的分解”方法来解决,“力的分解”与“力的合成”一样,实质都是利用平行四边形定则来解决问题的方法.由于待分解的力在问题情境中必定产生物理效应,或使受力物体产生加速度、或与周围其他物体存在相互作用,因此,“力的分解”可根据实际问题所需以及力所产生的物理效果综合确定其分解的方向,下面以一个具体案例进行分析.
案例1.当车在野外陷入泥坑时,有的人能够凭借一己之力将其拉出来,一个小小的力就能够产生大大的效果,这到底是怎么回事呢?如图3所示,将绳的一端绑在树干上,另一端绑在车上,给绳施加一个水平拉力F,当绳的夹角为2θ时,车刚好被拉出,求解车受到的拉力大小.

图3 徒手拉车出泥坑
3.1 力的合成解决途径
对节点O受力分析,如图4,节点O在拉力F与绳的张力T作用下处于平衡状态,利用力的合成,将两张力T合成得T合,根据余弦定理,有
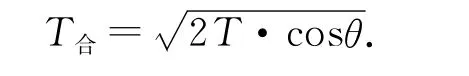
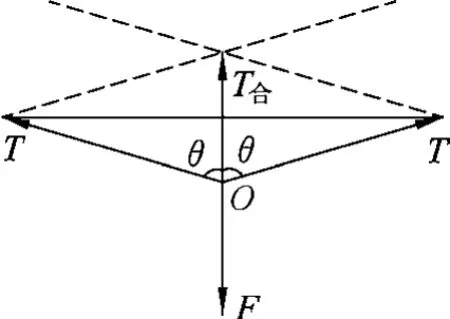
图4 拉车出泥坑力的合成受力分析
根据二力平衡,有T合=F.
3.2 力的分解解决途径

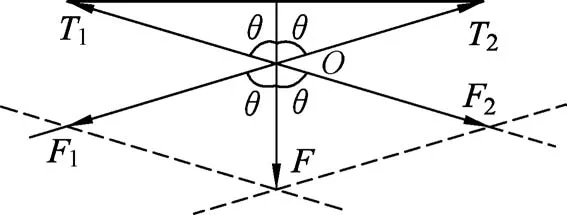
图5 节点O受力分析
如图6,当没有条件限制时,力F可以分解为无数对力.但在上述情境中,在力F的作用下,绳被拉紧,产生了沿绳的作用效果,绳中产生张力,将车从泥坑中拉出,进一步产生想要研究的物理问题:车被拉起时受到的拉力是多大?如图7所示,根据“问题解决需要”,力F的其中一个分力应该沿绳的方向,且与拉车的方向相同,即④的方向;根据“作用效果”确定另一分力的方向,其产生拉绳的作用效果,即应该是③的方向.

图6 拉车出泥坑“力的分解”受力分析
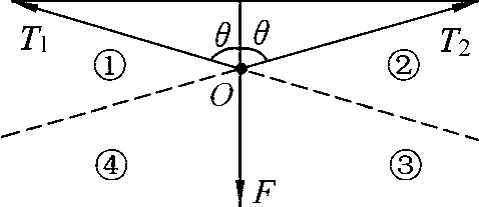
图7 分力方向的寻找
综上,可得以下结论:
(1)“力的分解”与“力的合成”一样,实质都是利用平行四边形定则来解决问题的方法.有时用“力的合成”会简单一些,有时用“力的分解”会简单一些,有时又需要将两者结合.
(2)③④的方向既是力的“作用效果”方向,也是“问题解决需要”所对应的方向,本质上两个分解依据间并不矛盾,而是统一的.所以,在进行“力的分解”时,可根据实际问题所需以及力所产生物理效果综合确定分力的方向.可先确定待求力的方向,基本就可确定其中一个分力的方向,另一个分力的方向则根据合力及其产生的实际效果去判断;如果所求解的问题对分力方向指向性不明显,则可直接按照待分解的力所产生的“作用效果”确定分力方向.即通过实际问题和相互作用效果综合判断两个分力的方向,再利用平行四边形法则求解其大小.
4 关于“力的分解”教学
4.1 “力的分解”一节教学类型
“力的合成”一节的教学包含“力的合成满足平行四边形法则”这一规律的学习,由于“力的分解”与“力的合成”互为逆运算,所以,“力的分解”一节中“力的分解满足平行四边形法则”可以依据“力的合成满足平行四边形法则”合理演绎推出,其正确性是由“力的合成满足平行四边形法则”提供保证的.
所以,“力的分解”一节课的教学重点不是“力的分解满足平行四边形法则”这一规律的学习,而应该是这一规律在实际问题中应用的学习.规律在实际问题解决中的“应用”,通常有提高解决此类问题效率的技能,也就是解决此类问题的方法,方法的使用应具有操作步骤.
应用“力的分解满足平行四边形法则”解决实际问题,其步骤可归纳为:(1)确定研究对象;(2)对研究对象受力分析;(3)选择已知的力(通常)作为需分解的合力;(4)由实际问题中待求力的方向、与研究对象存在相互作用的方向等,确定两个分力的方向;(5)按平行四边形法则,将合力分解到确定的分力方向;(6)运用力的平衡方程、相互作用力等知识求解问题.
4.2 “力的分解”一节教学目标
如前分析,“力的分解”一节主要涉及到“力的分解”概念、“力的分解”规律、“力的分解”规律应用的教学,其教学目标可表述如下.
物理观念:(1)理解“力的分解”概念,能举例解释“力的分解”适用的情境;(2)理解“力的分解”规律,能有依据地解释“力的分解”所满足的规律;(3)掌握“力的分解”规律解决问题的方法,能解释方法的步骤;在可用“力的分解”方法的场合,能遵循步骤依次选择出相应必要技能,正确分解受力.
科学思维:经历运用“力的分解”规律解决实际问题的过程,体会审题(确定对象)、分析题(确定物理过程)、列方程求解等物理问题解决方法的运用.
所以“力的分解”一节的教学重点在于“力的分解”规律应用方法的教学.
4.3 教学建议
由前述分析,本节课重点在于“力的分解”应用方法的教学.由于方法在运用时,具有潜在性,故以“方法”为目标的教学应该有一个显性化方法的条件和步骤的环节.[3]以下教学建议中,重点呈现目标3的实现.
关于“力的分解”一节教学,建议教学如下进行.
(1)前面我们学习了“力的合成”,两个分力与其合力之间满足平行四边形法则.
(2)已知一个力(视为合力),求解其分力的过程叫作“力的分解”.显然,“力的分解”是“力的合成”的逆运算.
(3)“力的合成”满足平行四边形法则,则“力的分解”也满足平行四边形法则.
(4)已知一个合力,求两个分力,就是将合力为对角线,找出成对邻边的过程.则能找出多少对邻边?
(学生活动,画出多组不同的平行四边形)
可得:由一个合力找出两个分力,可以有无数对的邻边.
(5)“力的分解”规律应用方法的教学.环节1:“力的分解”规律解决实际问题.
下面从解决两个实际问题出发,根据上述总结的“力的分解”应用于解决问题的方法,进行“力的分解”实质的教学.
案例2.
问题:当人用力F时,可产生的对车的拉力是多大?
对象:拉力作用的节点A,处于平衡状态.
受力分析:受3个力,即拉力,两段绳的弹力.
待分解的力:已知力F,待求的力是绳对车的拉力,可将F作为待分解的力,其中一个分力与待求解的力共线,可通过二力平衡和牛顿第三定律求对车的拉力.
确定分力的方向:根据“问题解决需要”,求解绳对车的拉力,即求绳中的张力,那么力F的其中一个分力方向与该绳共线.如图7所示,力F还对绳产生沿④方向的拉伸作用效果,则其中一个分力沿④的方向.另一分力方向也不能随意选择,而是要按照实际作用效果区分,或跟其他物体产生的相互作用区分.力F还产生了沿③方向的拉伸效果,则另一分力方向应为③的方向.
分解力:给出一组具体的数据,按平行四边形法则,借助三角函数关系求出该力.如此求出的两个分力,沿绳的力,恰好也是我们待求的拉车的力(具体求解见上述案例1的分解的解决途径).
案例3.如图8所示,工地上常常能够见到的塔吊,门口常见到的挡雨玻璃,请问塔吊是依靠什么样的力将重物提到高处呢?玻璃的重力是靠什么来平衡使其保持静止呢?

图8 工地上的塔吊和生活中的挡雨玻璃
问题解决过程如下.
环节1:模型构建及力的分解.
模型构建:上述两种情况都可简化为如图9的塔吊模型.

图9 塔吊模型分力方向的寻找
问题:求解C点拉力F的分力.
对象:与铅笔头末端接触的绳上节点,处于平衡状态.
受力分析:节点C处于平衡状态,合力为0,受拉力F,而在竖直向上方向显然没有直接的力与该力F平衡,根据实际情况,C肯定还受到沿①方向的绳子的拉力;如果要合力为0,还应受沿②方向的力.
待分解的力:已知的力只有拉力F,则待分解的力应该为F,与①②方向的力分别构成二力平衡.
确定分力方向:显然,根据实际情况,要使“力的分解”有实际物理意义,拉力F只能沿杆沿绳的方向分解,根据力的合成,合力在两分力所夹平行四边形对角线上,显然,只有③④方向的合力才可能为F,所以将F沿③、④方向分解.另一方面,课堂上让学生利用该简易模型,手指被向下拉,即③方向是绳被拉伸的方向;手掌与铅笔接触部分受到压力,故④的方向在F作用下,杆受力方向是向内压,所以力F产生沿③、④方向的作用效果,也能证明将F沿③、④方向分解.
根据二力平衡及牛顿第三定律即可求解另外两平衡力.
环节2:“力的分解”规律解决问题的方法的学习(显性化方法的条件和步骤).
师:前面解决问题过程中,解决的步骤有何共性?又是如何确定分力方向的呢?
本部分教学目的引导学生回忆以上两个问题解决过程,进一步总结应用“力的分解”解决实际问题具体方法(详细内容见4.1节归纳的操作步骤),如何根据问题情境及作用效果确定分力方向(具体方法见第3节的结论2).
环节3:“力的分解”解决问题方法的练习.
如图10所示,倾角为θ的光滑斜面上有一质量为m的物块,在以下两种情况下处于平衡状态,根据上述总结出的具体操作步骤,求解施加的外力大小.求
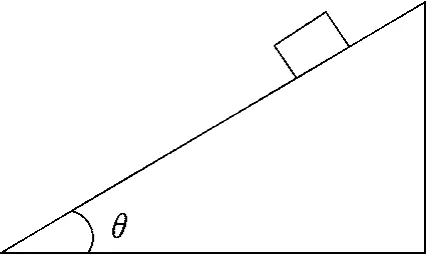
图10 斜面模型下力的分解
(1)施加沿斜面向上的拉力;
(2)施加水平向右的推力.
评析:上述教学以“力的分解”方法为教学目标,将“力的分解”应用到实际问题解决过程中,这样的教学目标定位准确,方法实施步骤清晰;此外,将“力的分解”两种依据综合起来进行教学,既避免了单一强调“按实际问题分解”或“按作用效果分解”存在的问题,还能知道“力的分解”目的是什么,能将“力的分解”知识的运用真正与实际问题解决联系.
5 总结
根据以上讨论,可得如下结论:
(1)“按实际问题分解力”“按力的作用效果分解力”不存在矛盾,困惑来源于教学中的单一强调.特定某个力的分解,应根据实际问题所需以及力所产生的物理效果综合确定分力的方向.
(2)“力的合成”与“力的分解”都是服务于解决具体物理问题的,本质都是平行四边形法则在解决问题中的应用.将力的合成与分解视为解决力学问题的内在一致性的两种方式是合理的.人教版新教材将两者合并为一节, 一定程度上体现这种思路.[4]所以“力的分解”教学本质属于“方法”的教学.
(3)学生应掌握“力的分解”解决问题的操作步骤,在可用“力的分解”方法的场合,能遵循步骤依次选择出相应必要技能,正确分解受力.可依照构建模型、明确研究问题、确定研究对象、受力分析、确定受力方向、利用三角函数和平行四边形法则求解分力大小的思路求解具体物理问题.
