一种改进型分区域光伏MPPT控制策略的研究

李月英，左明鑫

(郑州科技学院电子与电气工程学院，河南郑州 450064)

太阳能凭借其取之不尽用之不竭且绿色无污染的特点，成为新能源开发的重要方向之一，而光伏最大功率点追踪(MPPT)技术就是有效利用太阳能的重要途径。

目前，各种MPPT 控制技术层出不穷。文献[1-2]采用的定步长算法存在跟踪精度和稳态精度难以同时兼顾的矛盾，即步长过大，容易造成稳态震荡，步长过小，追踪速度会变慢；文献[3]采用自适应面积差法避免了传统算法动静态的矛盾，不但可以实现快速跟踪，而且稳态精度高；文献[4-5]中提出了改进型电导增量法(INC)，可以实时调整跟踪步长，同样具有良好的跟踪速度和稳态精度；文献[6]采用的变步长INC算法克服了动静态控制不可调和的矛盾；文献[7]采用的群粒子算法虽然能取得不错的效果，但是这些算法实际中难以实现。针对传统算法的问题，本文根据光伏组件输出电压、电流和功率的关系，把P-U 曲线分为线性区、最大功率区和急速变化区三部分，三个区域均采用不同的步长，在离最大功率点(MPP)较远的时候采用大步长以快速接近MPP 点，在MPP点附近，则采用小步长避免震荡。

1 光伏组件工程模型和工作特性曲线

1.1 光伏组件工程模型

光伏组件的工程模型如图1 所示。

图1 光伏组件电路模型

光伏组件的电流-电压关系如式(1)所示。

式中：Iph、I分别为光生电流、输出电流；Rsh、Rs分别为旁漏电阻、串联电阻；U为负载两端电压；K为玻尔兹曼常数，K=1.38×10-23J/K；q为电子电荷量，q=1.6×10-19C；T、A分别为光伏电池温度和二极管特性因子。

标准情况下开路电压(Uoc)、短路电流(Isc)、最大功率点对应电压(Um)、最大功率点对应电流(Im)，可以从光伏电池厂家处获取，简化式(1)，可得式(2)～式(4)。

1.2 光伏组件工作特性曲线

标准情况(1 000 W/m2，25 ℃)下，得到I-U、P-U、dP/dU-U和dI/dU-U的光伏组件输出特性曲线，如图2 所示。

从图2(c)可以看出，在P-U曲线左侧，P-U曲线几乎为一条斜率恒定的曲线，接近MPP 时，曲线表现为上凹特性，在MPP 附近曲线近似为开口向下的抛物线，在MPP 的右半侧曲线很陡峭，变化较急剧。因此，根据曲线输出特性，把P-U曲线分为三个部分：线性区、最大功率区和急速变化区。

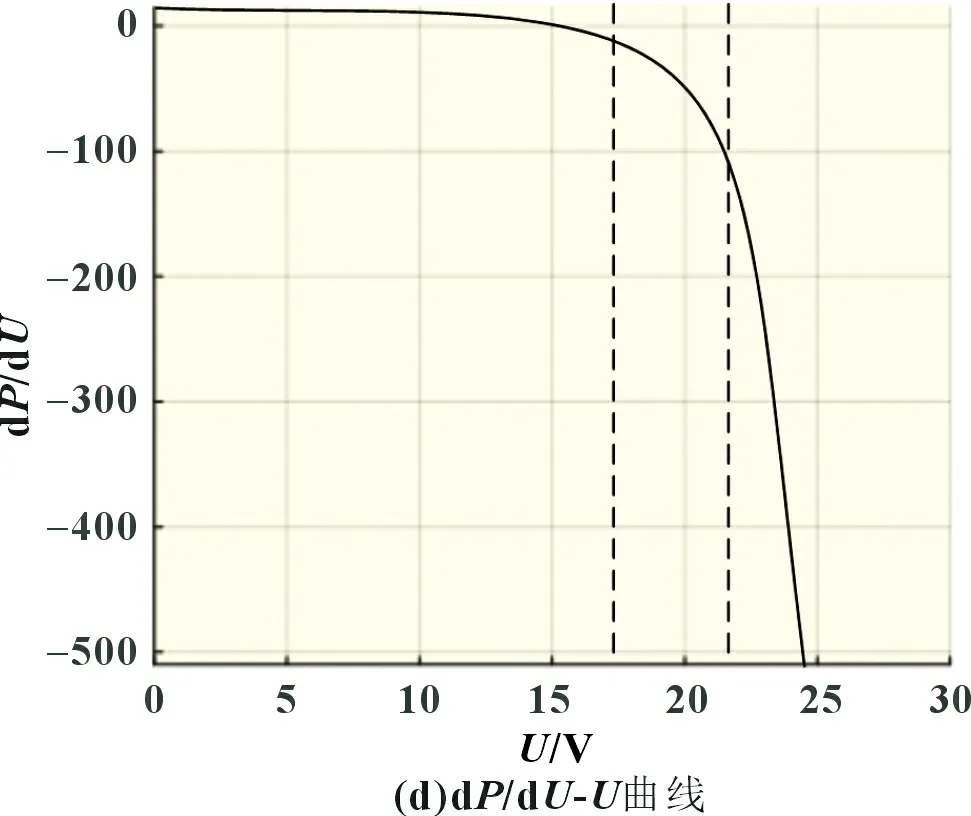
图2 光伏组件输出特性曲线

2 改进型MPPT控制策略

2.1 光伏曲线区域的判断

由图2 可以看出，通过判断实际工作点的位置，选择不同的步长。这里根据输出功率对输出电压的倒数来选择步长，由dP/dU=I+U×dI/dU得：

(3)如不满足条件(1)和(2)，则说明工作在最大功率区。

2.2 不同区域的步长选择

(1)线性区步长选择

由图2(c)可知，MPP 右侧曲线斜率绝对值是左侧曲线斜率绝对值的4 倍左右，由于线性区功率变化相对缓慢，因此左侧要想快速追踪MPP，步长应设置为右侧的4 倍。设急速变化区的步长为ΔU，则线性区步长为4ΔU，但是如果线性区的步长4ΔU太大，会导致在线性区末端处直接跨越最大功率区到急速变化区，因此线性区的步长4ΔU不能大于最大功率区的跨度。

(2)急速变化区步长选择

由前面的分析可知，急速变化区曲线较为陡峭，因此选择小步长为ΔU，防止在追踪过程中使实际工作点在线性区和急速变化区之间来回徘徊，造成能量损失和功率波动。

(3)最大功率区步长选择

由图2(c)可知，在最大功率区范围内，P-U曲线近似为抛物线，在这个区域范围内抛物线上选取3 个采样点，根据这3个采样点，利用牛顿差值法得到曲线函数多项式表达式，进一步通过多项式表达式求出极值点，即为最大功率点。

选取的3 个采样点分别为A1[x1，f(x1)]、A2[x2，f(x2)]和A3[x3，f(x3)]，可写出基于牛顿插值法的多项式公式：

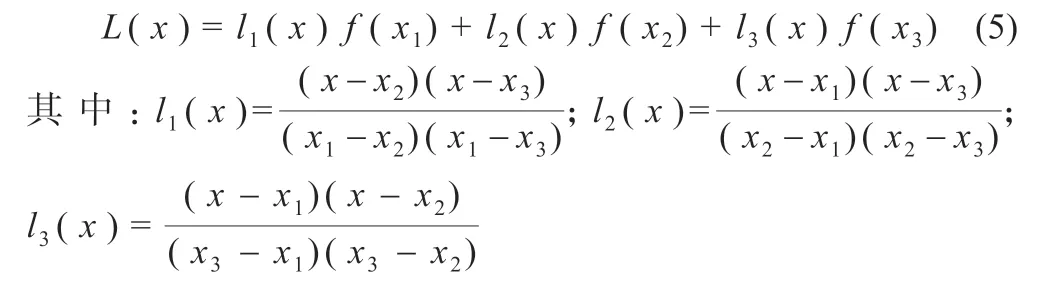
式(6)可进一步写出其对应的一般式：

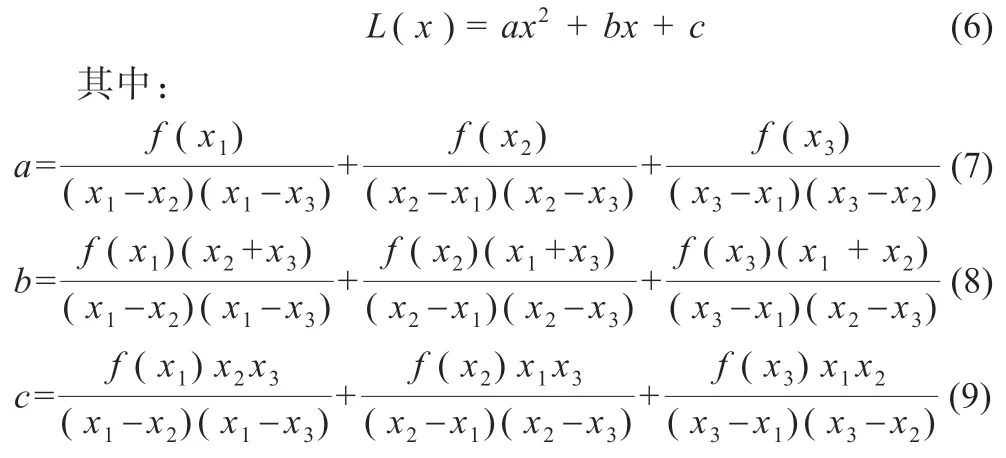
式(6)求导可得式(7)：

可得最大功率点对应的电压为xmpp：

由式(6)和式(11)可得，当xmpp=-b/2a，所拟合近似抛物曲线的极大值点为Lmpp[-b/2a，(4ac-b2)/4a]，此点就是MPP 的理论位置。因此，在进入最大功率区域内部时，只需要选择三个点，通过拟合曲线计算，就可以直接得到给定电压xmpp，从而精确定位出MPP。但是这三个点的选取不是随意三点，因为如果三点全部位于MPP 的一侧(例如全部在左侧)，那么拟合的曲线将计算不出MPP 对应位置。所以，选取的三点要分布于MPP 的两侧，就要加上三点的选取规则：被选取的三个点需要满足情况1 或情况2。

情况1：

情况2：

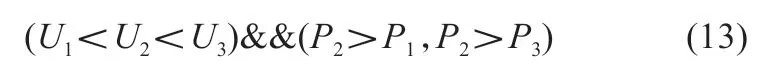
三个点只要满足情况1 或情况2，就能利用牛顿插值来拟合曲线，从而完成计算。

2.3 改进型MPPT 控制策略工作原理

实现改进型MPPT 控制工作原理如图3 所示。由图3 可知，首先初始化电压、电流和功率及其变化量的大小；在线性区和急速变化区的扰动方向由扰动法来确定，如果ΔP×ΔU＞0，则实际工作点在MPP 左侧，保持原扰动方向继续扰动；如果ΔP×ΔU＜0，则实际工作点在MPP 右侧，需要向原扰动方向的反向进行扰动；设定功率调整最小值ηU和电压调整最小值ηP，当功率和电压变化很小时，可认为已经追到MPP，此时实际工作点保持原地不动；当功率和电压变化超过设置阈值时，判断实际工作点所在区域，实行区域分步长控制。

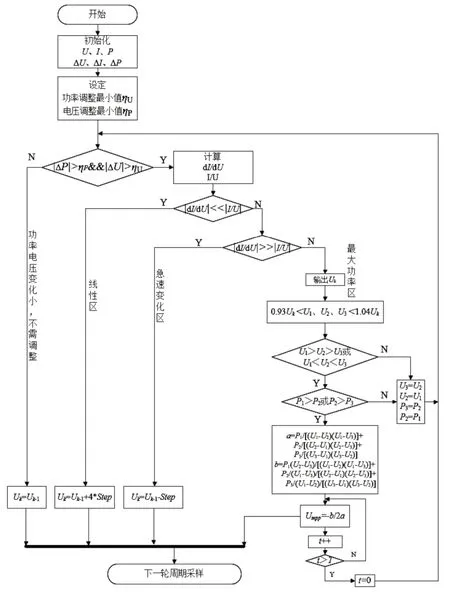
图3 改进型MPPT控制流程

(1)当|dI/dU|<<|I/U|时，判定为线性区，采用大步长实现快速追踪，步长大小为急速变化区的4 倍，设急速变化区步长为step，线性区采用的步长为4×step。

(2)当|dI/dU|>>|I/U|时，判定为急速变化区，采用步长step实现追踪，由于急速变化区曲线较为陡峭，因此步长step不能太大。

(3)当条件(1)和(2)都不满足时，说明此时进入了最大功率区，输出此时电压Uk，以Uk为基准，在0.93Uk和1.04Uk范围内，选取满足(U1＞U2＞U3)&&(P2＞P1，P2＞P3)或(U1＜U2＜U3)&&(P2＞P1，P2＞P2)的三个采样点：(U1，P1)、(U2，P2)和(U3，P3)，通过这个三个采样点利用牛顿插值法可以拟合出一个具有峰值的曲线。结合式(7)和式(8)，得到变量a和b的值，并且一次性定位到极值点Lmpp[-b/2a，(4ac-b2)/4a](即MPP 处)。由于外界环境实时变化，在Lmpp[-b/2a，(4ac-b2)/4a]保持周期时间T，不断重复图3 中的步骤。

3 Simulink 仿真和DSP 实验平台验证

3.1 Simulink 仿真结果分析

在Matlab R2017a/Simulink 中搭建MPPT 仿真平台，如图4 所示。光伏电池参数：Uoc=24.1 V，Isc=14.2 A，Um=18.92 V，Im=12.24 A。标准状况下(1 000 W/m2，25 ℃)，光伏电池输出功率为231.7 W；600 W/m2、25 ℃时，输出功率为152.8 W。Boost 电路参数设置：前级电容C=150 μF，后级电容C1=550 μF，电感L=15 mH，负载Rload=10 Ω。Simulink 仿真时间设置为1 s，功率调整最小值ηP=1 W，电压调整最小值ηU=0.5 V。

图4 Simulink 仿真平台

在Simulink 平台上，保持温度为25 ℃不变，通过设置光照强度(S)变化来观察输出功率波形；光照强度S设置为：0～0.4 s，S=1 000 W/m2；0.4～1 s，S=600 W/m2。图5、图6 和图7 分别为大步长(Step=0.6)扰动观察法、小步长(Step=0.01)扰动观察法和改进型MPPT 算法控制条件下的Simulink 仿真输出功率波形。

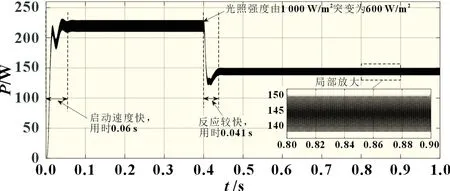
图5 固定大步长扰动观察法控制条件下的输出功率波形

由图5 可以看出，当采用大步长扰动法时，启动阶段到达新稳态用时0.06 s，跟踪速度较快，稳态震荡较大，当t=0.4 s时，光照强度由1 000 W/m2突变为600 W/m2，从突变开始到稳定后，用时约为0.041 s，跟踪速度相对较快，反应迅速。为了对比稳态震荡，统一在0.8～0.9 s 时间段内，对波形局部放大，此时功率在138.4～149.7 W 之间震荡，并没有真正跟踪到MPP，因为步长大，导致工作点越过MPP，反复在其左右侧来回跳动。

由图6 可以看出，当采用小步长扰动法时，启动阶段到达新稳态用时0.13 s，跟踪速度较慢，但稳态震荡较小，当t=0.4 s 时，光照强度由1 000 W/m2突变为600 W/m2，从突变开始到稳定后，用时约为0.07 s，跟踪速度相对较慢。在0.8～0.9 s 时间段内，对图6 中的波形局部放大，此时功率在147.3～151.2 W 之间波动，震荡现象不明显，基本追踪到了MPP。

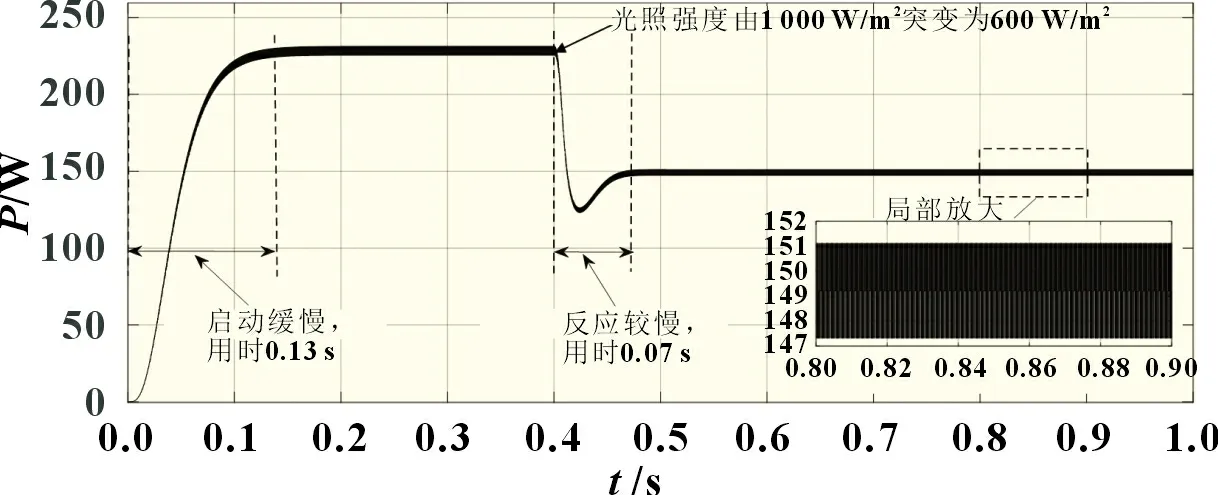
图6 固定小步长扰动观察法控制条件下的输出功率波形

由图7 可以看出，当采用改进型MPPT 算法时，启动阶段，稳定后用时仅为0.054 s，启动较快。从图7 中波形可以看出，稳定后波形震荡较小，当t=0.4 s时，光照强度由1 000 W/m2突变为600 W/m2，从突变开始到稳定后，用时仅为0.038 s，反应迅速。同样，在0.8～0.9 s 时间段内，功率在149.7～152.7 W，与小步长扰动法有着几乎相同的稳态效果。

图7 改进型MPPT控制条件下的输出功率波形

3.2 基于TMS320F28379S 平台验证

基于TMS320F28379S 平台搭建了基于Boost 电路的10 kW 光伏系统。Boost 参数如下：前级电容C=1 mF，后级电容C1=1.3 mF，L=2.2 mH，Boost 功率管开关频率f=40 kHz。为了便于比较，设置曲线1(Uoc=334 V，曲线适配比FF=0.75，Umpp=250 V，Pmpp=10 kW)和曲线2(Uoc=680 V，FF=0.75，Umpp=510 V，Pmpp=10 kW)，在直流源上把曲线1 切换到曲线2。图8 所示为三种不同控制条件下的输出结果。

图8(a)：固定大步长ΔU=10 V，曲线1 切换到曲线2，从曲线1 对应的稳态到达曲线2 对应的新稳态用时约为0.61 s，追踪相对速度较快，两种曲线下对应的稳态，输出电压和电流有一定的震荡，振幅较大。

图8(b)：固定小步长ΔU=5 V，曲线1 切换到曲线2，从曲线1 对应的稳态到达曲线2 对应的新稳态用时约为1.2 s，追踪速度较慢，反应迟钝，两种曲线下对应的稳态，输出电压和电流震荡小，稳态精度相对较高。

图8(c)：在改进型控制算法条件下，由曲线1 切换到曲线2 后，从曲线1 对应的稳态到达曲线2 对应的新稳态用时仅仅为0.48 s，追踪速度快，有着和固定大步长扰动法相近的动态特性；在保留大步长良好的动态特性基础上，稳态时输出电压和电流波形稳态精度较高。

图8 三种不同控制条件下的输出结果

由仿真和实验结果可知：

(1)仿真平台，通过判断|dI/dU|和|I/U|的关系，来确定实际工作点所在的区域。开始启动阶段，固定大步长扰动法、固定小步长扰动法和改进型MPPT 算法分别用时0.06、0.13 和0.054 s，固定大步长扰动法和改进型MPPT 算法具有相近的动态特性，跟踪速度比小步长扰动法提升了一倍左右。稳态方面，改进型算法稳态震荡范围(149.7～152.7 W)，幅度为3 W，远远小于固定大步长扰动法稳态震荡范围(138.4～149.7 W)，幅度为11.3 W。

(2)基于TMS320F28379S 实验平台，在曲线突然切换时，固定大步长扰动法、固定小步长扰动法和改进型MPPT 算法分别用时0.61、1.2 和0.48 s，见表1。稳态方面，改进型算法稳态震荡范围(9 800～9 980 W)，幅度为180 W，远远小于固定大步长扰动法稳态震荡范围(9 315～9 910 W)，幅度为595 W；固定小步长扰动法稳态震荡范围(9 678～9 969 W)，震荡幅度为291 W，但追踪速度较慢。通过实验对比可知改进算法兼顾了跟踪速度和稳态精度。

表1 实验平台三种算法对比

4 结论

仿真和实验表明：本文所提出的改进型MPPT 策略通过分区域分步长控制，在线性区和急速变化区，根据曲线特性，选取步长快速，进入最大功率区，保证了跟踪速度，即动态特性；在最大功率区，基于三个采样点，利用牛顿插值法拟合曲线一步计算出最大功率点，从而避免了稳态震荡；解决了传统控制算法对目标控制动静态难以兼顾的矛盾。