尊重学生“感知”让“建模”扎根思维的沃土之中——以吴正宪老师执教“乘法分配律”为例

●马贞，韩淑娴

《义务教育数学课程标准（2022年版）》在核心素养的主要表现及其内涵中指出，模型意识主要是指对数学模型普适性的初步感悟。知道数学模型可以用来解决一类问题，是数学应用的基本途径[1]。培养模型意识，发展“建模”能力是小学数学教学的难点之一。近期，听了全国知名特级教师吴正宪执教的“乘法分配律”，她在课堂上充分尊重学生感知，学生大胆地说、创造地想、热烈地辩，在充分感知的基础上从算式到文字、到图形、再到字母，逐步抽象概括，这样的“建模”遵循学生的认知规律，是有“根”的教学。现摘录其中的教学片段，与大家共享。

【课堂片断】

师：同学们，今天吴老师和大家一起学数学，大家一起看屏幕（图1）。

图1

师：你们看到了什么？看到什么就说什么。

生：左边花坛中每行有12朵花，总共有8行。

师：真好！不仅看到了花，还看到了重要的数据。你呢？

生：右边的花坛中每行有8朵花，总计有8行。

师：真棒！你们发现了这么多的信息。如果吴老师把左边的花坛覆盖了（图2），你们看到了什么？这个花坛的长是多少？

图2

生：这个花坛长12米，宽7米。

师：那你再看看这儿，你又看到了什么？

生：这个花坛长8米，宽7米。

师：同学们都睁大了眼睛，努力在情境中发现重要的数学信息。那你能提出什么数学问题吗？你想求什么？好，这个男孩。

生：我想求红花的宽跟长。

师：宽跟长已经有了，有了宽跟长可以求他们的什么？（周长）还可以求什么？面积还没学是不是啊？有没有会求的？你会求。

生：12乘以7。

师：哦，我明白了，你想求左边的面积。还有吗？你想求什么？

生：我想求黄花的面积，7乘以8。

师：有没有再勇敢点的。你想求左边，他想求右边，你还想求什么？

生：我还想求两块并起来的面积。

师：可以吗？除了面积，还可以求什么？

生1：我想求左边的花坛有几朵花。

生2：我想求右边的花坛有几朵花。

生3：我想求一共有多少朵花。

师：面对一个情境，我们从不同的角度可以提出很多问题。可以求左边和右边一共有多少朵花，还可以研究左边面积和右边面积一共有多少平方米。请你选择其中一个问题，能列综合式的尽量列综合式，听懂没？

【赏析】

设置对话情景，让学生站到课堂的中央，“你看到了什么”“你想求什么”“还可以求什么”，让学生发现信息，让学生提出问题，由学生寻找答案，有时学生的发言虽然不那么精确，但有着对数学质朴的理解，充满着浓浓的儿童味与生活味。吴老师的提问常常充满商量的语气，看似让学生选择，但学生实在无法拒绝吴老师期待与鼓励的眼神。

【课堂片断】

师：写一种方法就好！他求共有多少面积，跟他方法不一样的可以到前面来写。谁求花把手举起来，挥挥手。这是谁写的？你求的是什么？

生：我求的是花，我是这样想的。

师：不着急，上来就想当老师。你是这样想的，我们还没读懂呢！下面我们开始对话，谁来对他提问题？

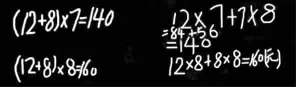
图3

生：12乘8是什么意思？

师：问得真好！我建议第一次掌声响起来。生：12乘8，意思是左边的花坛有96朵花。

师：谁支持他的观点？有问题吗？你们也是这么想的吗？接着问。

生：韩程阳，8乘以8等于几？哦，8乘以8是什么意思？

师：你这么一调整，问得就深刻了。还有吗？接着问。

……

师：问得真好！为什么把96与64加在一起？

生：我把左边和右边的花先求出来，然后再加。

师：都同意吗？这是谁写的，也是160朵，和大家讨论。

生：12加8什么意思？

师：问得好！你们可睁大了眼睛好好看啊！他说左边12朵，右边8朵，合在一起，这第一排是多少朵？还有问题吗？

生：为什么要乘8？

生：因为都有8行.

生思考。

师：思考就行了吗？还得亲自动手……说吧！

生：算一算。

师：我也特别喜欢你，真会听讲！

【赏析】

2.3.4 注意该区域范围历史沿革变化，重视口述文献的收集。在收集湘西地区红色文献时，地域范围不能局限于现在的行政区划，而应根据本地区的历史沿革等实际情况来确定。注意与湘鄂西、湘鄂川黔各红色纪念基地、老红军取得联系，实地走访，了解、记录红色口述文献。

课堂追问既是教学手段，也是教学艺术。“谁来对他提问题？”“还有吗？接着问。”“还有什么问题呀？”学生的回答不可谓不精彩，但吴老师并不满足，她总是不停地追问，让学生的思维向更深处漫溯。“问得真好！”“真会听讲！”吴老师善于用自己的眼神、手势、笑容鼓励学生、调动学生、影响学生。在吴老师的课堂，学生想说、敢说、善说，师生之间、生生之间充满温情与智慧。

【课堂片断】

师：好，该求面积的上来了，这是谁的？先说这个吧。

生：大家对我的算式有什么提问？

师：12乘7是先算出红花的面积，你问他能听懂吗？找那些没发言的人行吗？我建议那个男孩还没说过呢，很想听到你的声音！

生：7乘8是什么意思？

生：7乘8算出黄花的面积。

师：加是什么意思？

生：因为要算出总面积，所以应该把红花和黄花的面积加起来。

师：给点掌声吧！真挺好的，那这是谁写的？

生：这是我写的，有什么问题吗？

生：12加8是什么意思？

生：12加8的意思是红花的长和黄花的长相加总的长。

师：合起来了，那这个长就是几米了？宽呢？

生：宽是7米。

师：那20乘7就是什么？

生：这两块地的总面积。

师：听明白了吗？左边等于多少？右边等于多少？那你说这两个结果怎么样？（相等）

师：谢谢你支持我啊。你是说这个式子和这个式子是相等的对不对？我们写出几组算式了？有点感觉了吗？谁有感觉了把手举起来，有点儿感觉但说不出来的也请举手！

【赏析】

“很想听到你的声音！”“听懂了吗？”“给点掌声吧！”“谢谢你支持我啊。”吴老师善于“撩拨”学生的情绪，她的课堂语言很有亲和力，学生爱听。在吴老师的课堂，学生爱问、爱说、爱思考，这源于吴老师对孩子真诚无差别的爱与洞察，也源于吴老师对课堂与教材的深刻理解与把控。她的课看似平淡，但听着听着就有“感觉”了。

【课堂片断】

师：我们继续研究看看谁能再有新的感觉。你们看这儿，正面墙要贴瓷砖，侧面墙也要贴瓷砖，现在要求一共贴瓷砖的面积，会求吗？这次要求可高了，你能试着像刚才那样用两种方法来求吗？

图4

师：你们算出的面积是多少啊？

生：10平方米。

师：能说说你的算式吗？

生：2乘2等于4平方米，2乘3等于6平方米，加起来就等于10平方米。

师：你还想说点什么？你来说吧，还可以怎么样？

生：借助一张长方形纸和一张正方形纸，我把3米和2米墙合在一起，然后再乘那边的宽就得10平方米。

师：你一口气写了两个算式。你刚才在这儿犹豫了半天，你不回去，你想干吗呀？

生：我想问同学有没有不明白的地方。

师：掌声送给他！好，那这边跟这边又相等了，睁大了眼睛好好看，此时此刻你有感觉了吗？有感觉的人把手举起来，这么多人啊！

图5

【赏析】

乘法分配律的算理很重要，吴老师没有急于告诉或解释，而是借助两张纸，把两面墙合在一处，就题论理，以形象来支撑和发展抽象。一个“合”字形象而生动，自然贴切地“打通”了分步算式和综合列式之间的算理，在这里，抽象获得了形象的支撑。“此时此刻你有感觉了吗？”开始学生的感觉也许是懵懂、模糊、不具象的，但这种朦胧的感觉正是“建模”的基础。

【课堂片断】

师：现在我们又提出了新的要求，没有情境了，也不贴瓷砖了，也不数花朵了，也不求面积了。你有感觉了，你能遵从你的感觉再写出一组这样的式子吗？（学生尝试写）

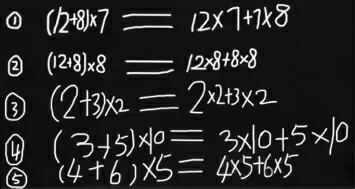
图6

师：我们先看看这两个同学的吧，3加5的什么？

生：3加5的和乘10就等于3乘10加5乘10。

师：你就这么轻易地画了一个等号？你为什么用等号连接啊？

生：我是这么想的，3加上5等于8，再乘10就等于80。

师：明白了，他是真正去算了的。同学们我们过去学过乘法呀，谁能换个角度来解读这个算式？有没有从乘法意义的角度去理解的？

生：3个10加5个10等于8个10，左边呢也是8个10。

师：掌声还不响起来！他能用自己的经验、过去的知识解读今天遇到的新问题。我们看第五个式子。左边几个5？再看右边，这是几个5加几个5？合在一起是几个5？

师：这就是填等号的重要原因，对吗？如果让你们继续写下去，还能写吗？写到今天下课？写到明天上课？那能写出多少啊？

【赏析】

学生“原生态”的思考弥足珍贵，看似五花八门、雾里看花，但仔细观察，还是能看出端倪[2]。“你有感觉了，你能再写出这样的一组式子吗？”“感觉”是什么东西，这还真不容易说清楚，但学生听明白了，你们看，孩子们写出来的“感觉”、说出来的“感悟”多好啊，这不仅是对乘法分配律的“模仿”，更是一种基于感性的“数学表达”。

【课堂片断】

师：那好，这一类的问题，有没有共同的规律？你能把这个共同的规律用你的语言写出来吗？

生：我发现结果是一样的，而且写不完。

师：这个发现多了不起啊！我要追问了，那我说3加5等于几？7加1等于几？这结果也一样呀，它跟我们今天学的有什么不同？你得把这个过程用我们的语言表达出来。

生：我发现他们其中的一个数是一样的。

师：你发现了他们其中的一个数是一样的，这很重要。比如说第一题的哪个数是一样的？

师：再来看这一题，就是两个数的和都乘一个数是这意思吗？你还有什么发现？

生：我发现两个物体的长加在一起再乘以宽就等于总面积。

师：挺好的，你发现两个物体的长合在一起乘宽就等于总面积。还可以怎么样？

生：还可以先求一个物体的面积，再求另一个物体的面积，然后加起来。

师：越来越发现新东西了，谁能把这一类的题用一句话做总结？

生：分配率。

师：你说的？有戏！但不是你那个率啊。

生1：这一类问题两组数既可以分开算，也可以一起算，而且结果一样，写不完。

生2：两个算式有一个数肯定是一样的。

师：有点儿意思。他说这一类的问题两组数可以怎么样？你来说。

生：可以分开算，也可以合起来算。最后的结果一定是一样的。

图7

师：真棒！真是越总结越完善。

【赏析】

“你能把这个共同规律用你的语言写出来吗？”自己的语言是学生听得懂的语言，在这样的课堂里，大家一起“聊”数学，有一种熟悉的“家”的味道。“我要追问了。”吴老师的追问总能抓住学生的“痒处”，引导学生的思维向更深处漫溯。“你能把这个过程表达出来吗”“你还有什么发现？”“谁能把这一类题用一句话做总结？”儿童化、生活化的提问让孩子们听起来特别亲切。数学语言的本质是一种数学模型，它是沟通数学与现实世界的桥梁[3]。学生的回答虽不十分准确，但核心要义达到了，这是孩子们对乘法分配律的“儿童化表达”。

【课堂片断】

师：你们都是这么想的吗？北京有一位同学是这样写的，爸爸和妈妈合在一起疼我，然后他说爸爸疼我，你们接着说，应该怎么说？

图8

生：妈妈也疼我。

师：他们一起疼我。这好记吧？那你说这个爸爸可不可以代表12？可以代表上式中的2吗？代表3、4可以吗？这个妈妈可以代表8吗？代表3、5、6可以吗？谁能比他写得再好点？我不用文字表示，还可以用什么表示？

生：图形。

师：接着写，图形怎么表示？〇表示谁？

生：表示爸爸。

师：爸爸表示谁？（其中的一个数）然后再加上一个△，三角形表示什么？（妈妈，也是其中的一个数）然后呢？

生：再乘☆。

师：五角星又表示什么？

生：就是两个算式里面一模一样的那个数。

师：你的意思就是这个7对不对？然后等于什么？这很关键。大家一起来说！

生：等于圆乘五角星，再加三角形乘五角星。

师：那你说你这个可以表示多少个式子？如果我不用图形表示，还有新的表示方法吗？你想用什么？

生：字母。

师：来，你就当着大家一起来写啊。好，不许你写了，大家一起接着写下去。

生：等于a×c加b×c。

师：我们能把这句话说出来吗？跟着我试试说好吗？两个数的什么？乘一个数等于什么？再把两个结果怎么样？他们的结果变不变？这就是什么？

图9

生：乘法分配律。

师：我们今天学习了什么？乘法分配律能解决什么问题呀？让我们带着这一个个的问题和期待，回到生活中去找一找，看看在哪儿能用到它，好吗？

【赏析】

数学在本质上就是在不断的抽象、概括和模式化的过程中发展、丰富起来的。数学学习只有深入到“模型”“建模”的意义上，才是一种真正的数学学习[4]。“北京有一位同学是这样写的”把孩子们的思维从具体算式引入到文字表述，它代表的不再是一道道算式了，而是一类现象，孩子们说得很好、很到位。“谁能写得比他更棒点！”在吴老师的“撩拨”下，孩子们思维空前活跃，又想到了图形、字母，它反过来验证了前面讲到的所有算式。至此，乘法分配律的“模型”水到渠成，并深深扎根于学生的头脑之中。