“3D模型”中的转化思想

黄义添

对于一个图形，当我们从几个不同方向看它时，就可能会有不一样的图形呈现出来。

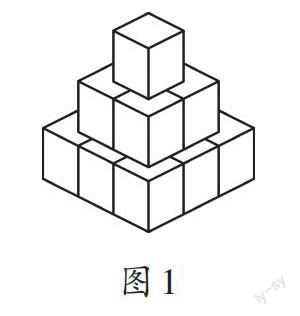
例如，把14个棱长为1cm的正方体木块在地面上堆成如图1所示的几何体，然后向露出的表面喷漆。若1cm2需用漆2g，则给该几何体喷漆需用多少漆？

第一眼看上去，我们可能会感觉无从下手，因为图1所示的几何体虽然由小正方体堆积而成，但有些露出来的面只是小正方体的部分表面，所以整个几何体的表面积并不好求。那我们该如何解决呢？

这时，我想到了移动，即把每层的小正方形都移动到一个角落，这样露出来的面都是小正方体的整个面了。

移动后，要求几何体表面积，还得观察。

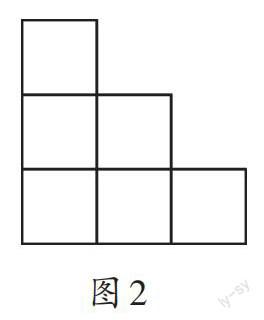
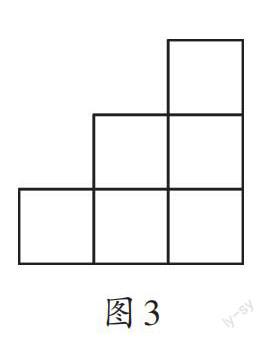
移动后的主视图（如图2）一共有6个小正方形，因为几何体前后视图一样，所以我将它乘2。同理，移动后的左视图（如图3）也有6个小正方形，也可以乘2，这样前、后、左、右加起来就有24个面。接下来是俯视图（如图4），有9个小正方形，又因为底面不需要喷漆，所以这个几何体的表面就有33个小正方形。

由题意得，每个小正方形的边长是1cm，所以要求的几何体的表面积是33cm2。又因为每1cm2用漆2g，那么整个几何体需要用漆33×2=66（g）。

老师说，解决这类问题，还能用割、补、分、合等方法，这些都属于转化法中的一种。看来，形成一种转化思维才是最根本、最重要的。

教师点评

数学是一門基础学科，在生活中处处可见。在学习数学的过程中，充分调用已有的学习和活动经验，通过知识的再组合，形成解决问题的新办法，是提高我们思维水平的重要途径。

（指导教师：王 磊）