走近几何体，建立空间观念

李彤

一、几何体的展开与折叠

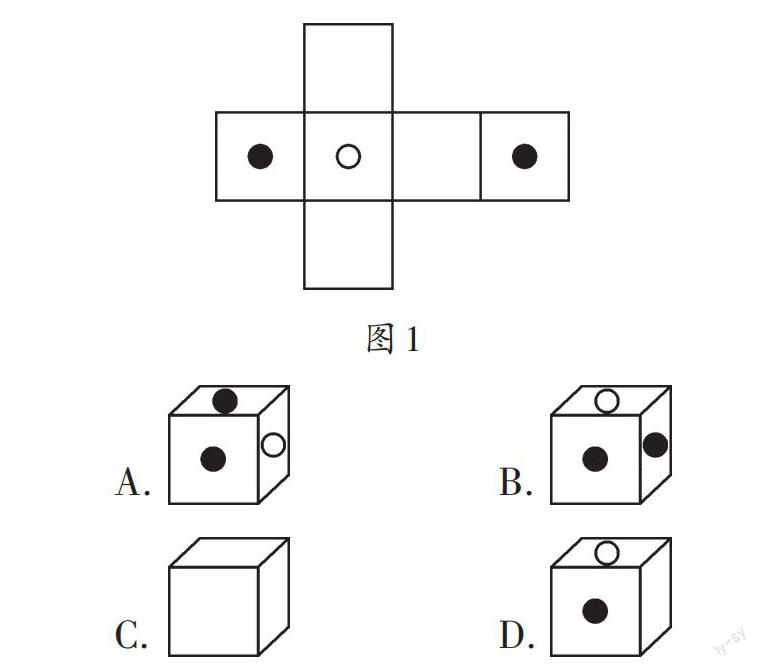
例1 图1是一个正方体纸盒的外表面展开图，则这个正方体可能是（ ）。

【解析】根据几何体的展开图，先判断实心圆点与空心圆点的位置关系：相鄰与相对，进而得出结论。

图1中，有1个实心圆点与1个空心圆点相对，而选项A和选项B中，实心点和空心点均是相邻的情况，没有相对的情况；选项C中，虽然看见的3个面上既没有实心点，也没有空心点，但可以判断出看不见的3个面上有2个实心点和1个空心点，实心点与空心点也有相邻的情况，但没有相对的情况；选项D中，1个实心点和1个空心点是相邻的，那么，还有1个实心点有可能会出现与空心点相对的情况。故只有选项D符合题意。

【点评】本题考查正方体的展开图。同学们都知道，正方体有11种展开图，而此题中的展开图最常规。故我们还可以从实物出发，结合具体问题，辨析几何体的展开图。通过立体图形与平面图形的转化，建立空间观念，是解决此类问题的关键。

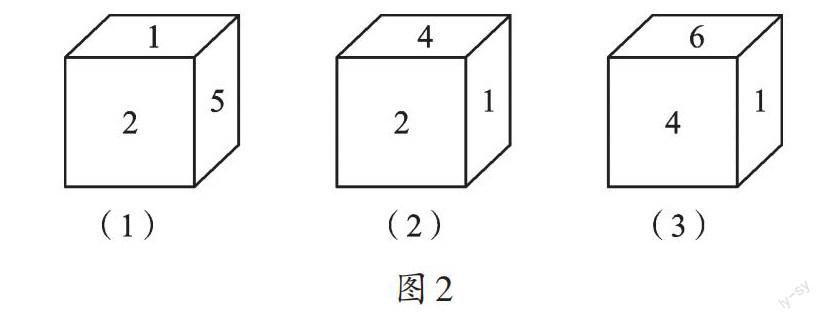
例2 已知一个不透明的正方体的6个面上分别写着1—6六个数字，图2是我们能看到的3种情况，那么数字5对面的数字是（ ）。

A.6 B.4 C.3 D.6或4或3

【解析】本题可以从图形进行分析，结合正方体的基本性质，得到底面的数字，从而求得结果。

由题意知，不同的面上写的数字各不相同。观察图形，每个正方体都有1，且和1相邻的数字有2、4、5、6，所以可推出1对面的数是3，即第一个正方体的底面数字为3。同理可知，与4相邻的数字是1、2、3、6，所以4对面的数字是5。故选B。

【点评】同学们首先要能通过题中的已知条件，分析出1的对面是3，再结合图形的展开与折叠，推出4的相邻数字。展开、折叠有助于我们感受立体图形与平面图形之间的关系，经历、体验图形的变化过程，发展空间观念。

二、由三视图判断几何体

例3 从正面、左面、上面观察一个由小正方体构成的几何体，依次得到以下形状图，如图3所示，那么构成这个几何体的小正方体有（ ）。

A.4个 B.5个 C.6个 D.7个

【解析】由主视图易得这个几何体共2层，由俯视图可得第一层正方体的个数为4，由主视图和左视图可得第二层正方体的个数为1。相加，那么共有小正方体4+1=5（个）。故选B。

【点评】本题主要考查同学们对三视图的掌握程度和灵活运用能力，同时也考查了同学们的空间想象能力。由主视图能看出几何体的列数和层数，由左视图能看出几何体的行数和层数，由俯视图能看出几何体的行数和列数，这也是我们常说的“主看列，左看行”。

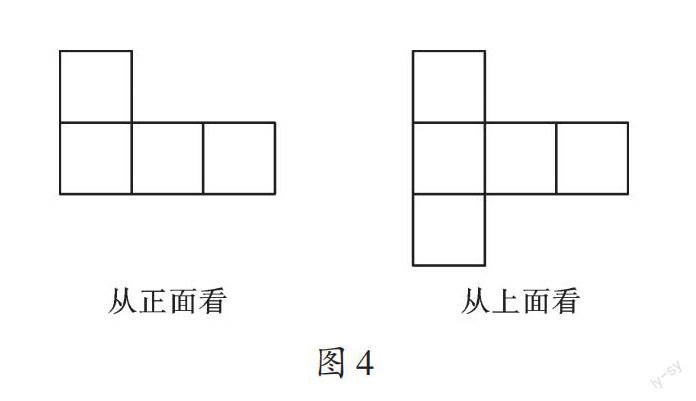
例4 一个几何体由若干大小相同的小立方块搭成，如图4，分别是从它的正面、上面看到的形状图，那么搭成该几何体最多需要小立方块______________个，至少需要小立方块______________个。

【解析】根据题意，可以先画出左视图，然后将列数和层数标注在俯视图里，就可以综合分析出结果了。

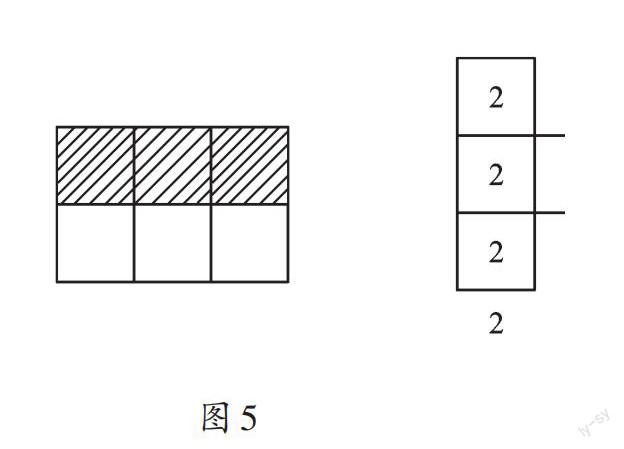
根据主视图和俯视图，可以画出左视图，如图5所示，阴影部分的小立方体至少有一个。在俯视图的下方，从左到右标出主视图每列个数；在俯视图的右侧，从上到下标出左视图每列最多的个数。若对应的数相同，则取相同，若不同，则取最小。然后，在俯视图上每个方格里填上相应数字，正方形内所有数字之和就是构成几何体最多需要的小立方块个数：2+2+2+1+1=8（个）。因为左视图第一列是2个，再由俯视图，可以看出每层最少有1个，所以至少需要小立方块个数为：2+1+1+1+1=6（个）。

【点评】本题考查由三视图判断几何体，由三视图想象几何体的形状，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合考虑整体形状。

（作者单位：江苏省灌云县教师发展中心）