“循环组”助我找规律
2023-02-15刘熠
初中生世界·八年级 2023年2期

找规律问题一直是一种常见的题型,在每一章的练习中,我几乎都会遇到。这不,在学习平面直角坐标系之后,又出现了一类点运动后坐标的变化规律问题,我把这种固定次数运动形成的循环称为“循环组”。果然,熟悉这类规律,问题都可以顺利解决。下面,我们一起看看两道例题。
例1 如图1,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过2022次运动后,动点P的坐标为________________。
首先,我们要找出“循环组”:从图中可以发现,每两个三角形是一组循环,也就是说,每4次运动为一组循环。其次,由2022=4×505+2,可知动点P运动到第506组循环中的第2个点,该点的纵坐标为0,横坐标即为2022。
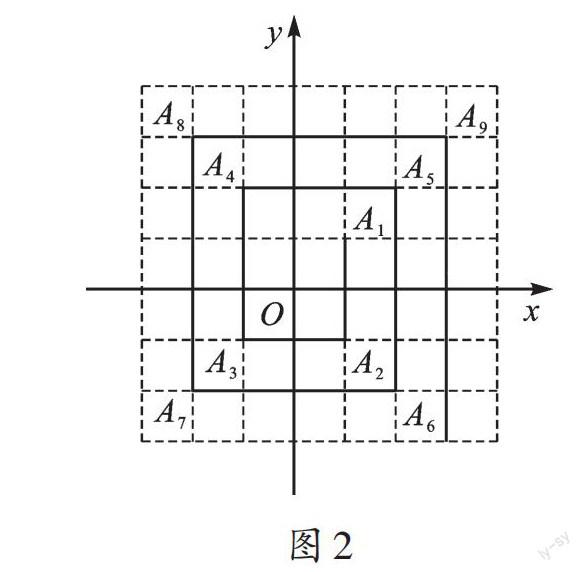
例2 如图2,在平面直角坐标系中,点坐标依次是A1(1,1),A2(1,-1),A3(-1,-1),A4(-1,2),A5(2,2),…,An,按此規律排列下去,则A2022的坐标是________________。
观察图形,我发现,A1、A2、A3、A4、A5……每4个点是一组循环。因为2022=505×4+2,所以A2022是第506个正方形的顶点,且在第四象限,即A2022的坐标为(506,-506)。
教师点评
刘熠同学善于总结,从发现“循环组”的角度看清了一类坐标系中的规律问题。虽然她所举例的题来自课堂学习或者课后作业,但她并不满足于作业或习题结果的获得,而是对练过的习题进行归类梳理,纳入自己的“知识体系”,这样的学习方法一定是“事半功倍”的,值得其他同学学习。
(指导教师:刘海兵)
