负阻态忆阻Hopfield 神经网络动力学
2023-02-15刘益安马瑞辰胡绍刚
刘益安,马瑞辰,李 国,于 奇,刘 洋,胡绍刚*
(1. 电子科技大学电子科学与工程学院 成都 611731;2. 电子科技大学重庆微电子产业技术研究院 重庆 高新区 401332)
生物神经网络拥有大量的神经元(~1011)以及突触(~1014),并且彼此之间形成错综复杂的连接,是一个庞大的非线性网络系统。研究表明,人类大脑的运行机制与神经元和神经网络的动力学行为密切相关[1-2],而且已被证实大脑中存在混沌现象[3]。为了揭示大脑的工作机理,神经网络动力学行为研究成为人工神经网络领域的重要内容,而忆阻器具有集成度高、可模拟突触可塑性、非易失性等特点,被认为是最有潜力的神经形态器件[4],并且其良好的非线性是研究人工神经网络动力学的重要条件。
1971 年,文献[5-6]发现了第4 种基本元件,即忆阻器,其阻值可变且保持记忆功能。2008年,惠普实验室研制出首个忆阻器件[7],后续产生了大量关于忆阻器的研究成果[8-10]。虽然惠普忆阻器模型作为使用最广泛的忆阻模型之一[11-12],但推导一个完全表征惠普忆阻器的数学模型是一项具有挑战性的任务[13-14]。因此,将非线性二次模型和三次模型等简化模型用于忆阻器电路的理论定量分析[15-16],会导致许多应用的结果不能令人满意。为了缓解这个问题,文献[17]提出了一种新的非线性对数模型来表征忆阻器,文献[18]提出了具有负阻态功能的忆阻器模型,能够更加准确地模拟突触可塑性和非线性脉冲激励神经元功能。
目前关于忆阻器神经网络的研究涵盖了广泛的主题[19],其中忆阻Hopfield 神经网络(Hopfield neural network, HNN)表现出丰富的动力学行为,并在解决组合优化问题和图像复原领域具有优势[20-23]。1990 年,文献[21]首次将混沌引入HNN,开启了HNN 丰富的动力学行为研究。2011 年,文献[24]将忆阻器引入HNN,并利用严格的数学证明分析了网络的动态行为,并以两个神经元数值实例进行了验证。2014 年,文献[25]利用忆阻器替换HNN 的一个权值,构建了一个3 神经元的简单网络,使得网络表现出准周期轨道、混沌以及超混沌等复杂的动力学行为。2016 年,文献[26]将忆阻器三次方数学模型带入HNN,并通过相轨图、庞加莱映射图和Lyapunov 指数对网络的动态特性进行研究,获得了不存在平衡点的超混沌吸引子。2020 年,文献[27]利用一种耦合双曲线忆阻器等效电路来模拟HNN 的突触串扰,并在不同串扰强度下观察到HNN 的多重稳定性、不对称吸引子和反单调性。
本文在前期提出的具有负阻态功能的忆阻器模型基础上,为了更好地模拟突触可塑性以及增加网络的负反馈功能,构建了基于忆阻器的新Hopfield神经网络模型,并对网络动力学行为进行了分析研究。实验结果表明,提出的忆阻Hopfield 神经网络模型具有丰富和复杂的动力学行为,为后续该神经网络在模式识别、数据处理、图像加密等方面的研究打下了坚实的基础。
1 具有负阻态的忆阻器模型
1.1 忆阻器模型
由忆阻器的初始定义可知,它是满足 φ −q域特定关系的一种器件,但为了进一步丰富忆阻器的内涵,文献[6]又提出了广义忆阻器的概念,即一个忆阻系统的定义应该满足如下关系:

式中,u(t)和y(t)分别为系统的输入信号和输出信号;x为系统的n阶状态变量;g为一个n维的连续向量函数;t为时间。
磁通或电压控制型忆阻系统的关系可写成:
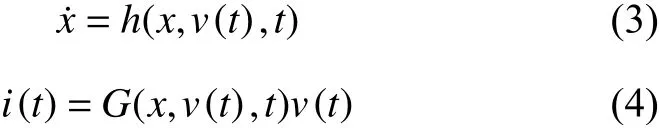
式中,h为一个n维的连续向量函数。此时的忆导值G也不再仅由磁通量 φ决定,而是由状态变量x、输入电压v以及时间t共同决定。
由上述定义可知,广义忆阻器将影响忆阻值的变化因素增多了,本文提出的改进模型就是对状态变量x进行了有效调整,使忆阻器能够呈现出正负两种阻态,消除了对理想忆阻器电导极性的限制。
如图1 所示,新忆阻器模型可以视为夹在两个金属电极之间的厚度为2D的半导体薄膜,包括一个正电导区和一个负电导区(每个区的厚度为D)。它也可以视作两个理想忆阻器背靠背连接,一个具有正电导,另一个具有负电导。忆阻器的电导由状态变量x确定,并且x的调控范围从原理想状态忆阻器的[0,D]扩展到[−D,D]。
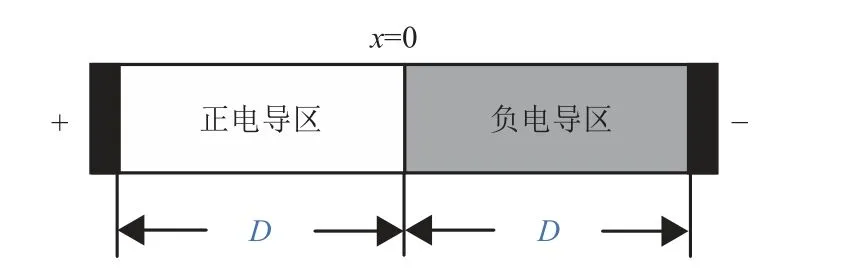
图1 忆阻器模型物理结构图
假设只考虑最简单的欧姆电导情形,G(x)定义为与状态变量x成正比,即G(x)=ax,其中a是常数系数。同时在实际忆阻器使用中,特别是氧化物类忆阻器,其两端的电阻或者电导经常会随着时间的推移而逐渐降低,所以可以通过引入衰减项(bx)模拟这种阻值变化,其中b为衰减系数。综上所述,改进的忆阻器可以描述为:

除了两个端点−D,D外,状态变量x与通过忆阻器的磁通量成正比。在改进的忆阻器模型上施加外部电压,可以使x的位置发生变化,从而改变忆阻器电导的大小与极性。如假设a=1 且b=0,如果在忆阻器上施加正电压,x向阳极移动,电导可能处于正阻态,反之若施加负电压,x向阴极移动,电导就可能处于负阻态。
1.2 器件模型仿真
当对改进的忆阻器施加一个正弦电压v(t)=Asin(ωt)时,可以得到忆阻器的电导公式为:

式中,c是常数系数;A、ω 分别为正弦电压幅度、频率。设置c=1,A=2,ω=2π,x0=−0.5,相关测试结果如图2、3 所示。若b=0,即忽略衰减项,通过绘制电流与电压的关系,可获得呈水平8 字状的捏滞回线,I-V曲线跨越所有4 个象限,且主要在2、4 象限,与原理想忆阻器模型仅在1、3 象限的斜8 字I-V曲线相比具有明显不同的特性,也意味着所提出的忆阻器模型具有负电导。此外,若b=0.08 时,施加正弦电压,可以获得多个连续的稳定状态。

图2 忆阻器电流电压曲线图(a=1, b=0)

图3 忆阻器电流电压曲线图(a=1, b=0.08)
2 忆阻Hopfield 神经网络
选取3 个神经元的连续型Hopfield 神经网络[28],表达式为:

式中,Ci为 第i个神经元的输入电容;ui为第i个神经元的输出变量;Ri为第i个神经元的传输电阻;wij为 神经元的连接权值;f(u)为神经元激励函数;Ii为神经元外部激励。为简化计算过程,通过单位归一化后,设置Ci、Ri均为1,Ii为 0,f(u)为双曲正切函数,即f(u)=tanh(u)。
Hopfield 网络是一种全连接的反馈型神经网络,每个神经元与其他所有神经元相互连接,3 神经元HNN 需要9 个突触连接权值。忆阻器本身具有阻值记忆特性,是良好的突触仿生器件,以往的忆阻器基本只有正阻态,而反馈型神经网络,特别是混沌神经网络,往往需要负反馈权值。由于忆阻器的电导与权值具有相同的量纲,可以将具有负阻态的忆阻器替换HNN 的一个权值,新忆阻Hopfield神经网络表达式为:

式中,u为输出变量矩阵;W为连接权值矩阵。可以表示为:

由式(10)、(11)可知,新网络的演化情况由系统初始值、权值矩阵W以及忆阻器参数a、b确定。
3 网络动力学特性分析
首先基于实验室24 核48 线程AMD 3960X 服务器平台,使用粒子群算法,搜索新HNN 模型比较优化的参数配置。设置a=1,b=0.05,初始值u(0)=(0.1,0.1,0.1),W权值矩阵为:

系统仿真时间为500 s,时间精度为1 ms,各参数采用国际标准单位归一化,无量纲。如图4 所示,系统的相位轨迹图呈现出普通的单涡卷吸引子,但单纯从相轨图还不能判定是否为混沌系统,还要结合Lyapunov 指数的正负情况。根据式(10)求得系统的Jacobian 矩阵,再利用施密特正交化方法,求解系统的Lyapunov 指数[29]。如图5 所示,系统最终的Lyapunov 指数分别为LE1=0.012 5,LE2=−0.003 4,LE3=−0.068 5,LE4=−6.891 2,存在大于零的Lyapunov 指数,所以可以初步判定系统达到混沌状态。

图4 系统的相位轨迹图

图5 Lyapunov 指数图
3.1 忆阻器参数的影响
通过调整忆阻器参数a,b的值来观察忆阻器对系统动力学行为的影响。如图6 所示,其他实验条件不变的情况下,a取[0.5, 1.5],步长为0.01,当a从0.50 增加到1.09,系统的Lyapunov 指数变化不大,LE1、LE2、LE3在零附近,LE1始终略大于零;当a从1.09 增加到1.50,系统的Lyapunov指数发生较大变化,且都小于零。

图6 Lyapunov 指数随a 值变化的曲线图
如图7 所示,b取[0.05, 0.12],步长为0.001,b的取值持续对Lyapunov 指数造成影响,证明忆阻器的衰减项对系统的影响较大,但不论b取何值,LE1始终大于零,其他Lyapunov 指数小于零。

图7 Lyapunov 指数随b 值变化的曲线图
3.2 连接权值矩阵的影响
神经元间的连接权值矩阵对系统有较明显的影响,实验中搜索出另一组连接权值矩阵Wn如下:

如图8 所示,系统呈现出图4 类似的单涡卷吸引子相轨图,且只有LE1=0.008 9,大于零,其他Lyapunov 指数均小于零。
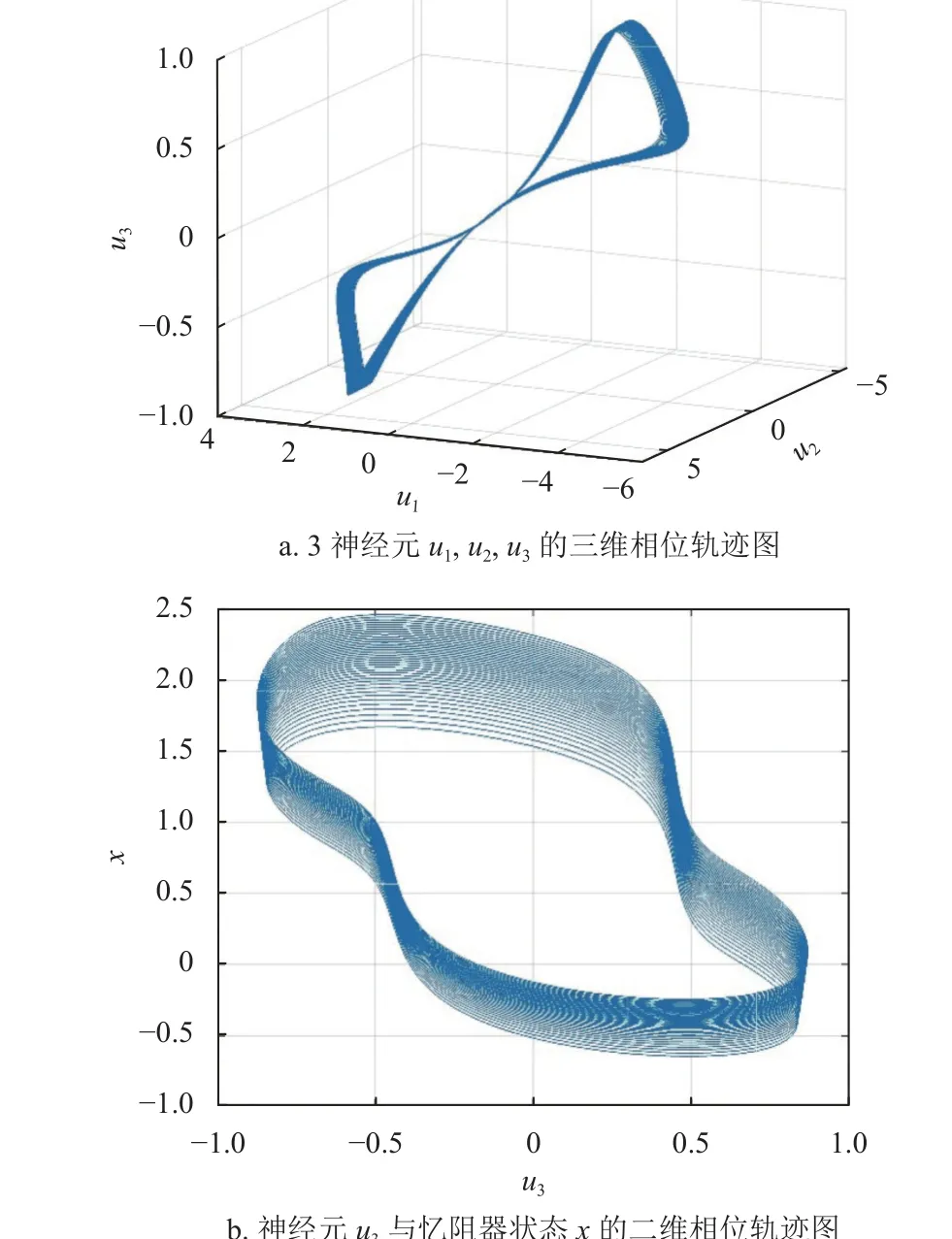
图8 系统的相位轨迹图(W 取Wn)
3.3 与其他Hopfield 神经网络对比
如表1 所示,Hopfield 神经网络的相轨图主要集中表现为单、双涡卷吸引子,Lyapunov 指数一般只有一个为正。文献[21]是最早将混沌引入HNN网络的,但10 神经元模型的动力学行为并不显著,而后续的改进模型性能都有所提升。

表1 本网络与其他HNN 模型的动力学特性对比
4 结 束 语
本文通过对具有负阻态的忆阻器模型进行数学分析以及I-V特性仿真测试,进一步明确了忆阻器的器件特性,同时基于该忆阻器模型构建了新的Hopfield 神经网络,并对网络的动力学行为进行了分析与讨论。实验结果表明,提出的Hopfield 神经网络模型具有丰富且复杂的动力学行为,并存在一定的混沌现象。同时,讨论了在不同的忆阻器参数以及连接权值矩阵条件下,网络的动态演化进程以及Lyapunov 指数的变化情况,并与同类型网络进行了对比,结果进一步表明该模型的有效性,为后续在模式识别、数据处理以及图像加密方面的应用提供了研究思路。
