面向旅客到达晚点最小的高速铁路列车运行图冗余时间布局优化研究

周政铎，周黎，李博

(1.中国铁道科学研究院 研究生部，北京 100081；2.中国国家铁路集团有限公司 科技和信息化部，北京 100844；3.中国铁道科学研究院集团有限公司 运输及经济研究所，北京 100081)

0 引言

列车运行图在实施过程中，不可避免地会受到各种随机因素的影响，导致列车发生初始晚点，还可能进一步传播发生连带晚点。铁路编图工程师在编制列车运行图时通常会进行“撒点”，即在区间运行标尺基础上设置额外运行时间。定义此额外运行时间为列车运行图冗余时间。轻度晚点发生时，调度员通常令列车按原计划顺序开行，利用冗余时间吸收晚点。然而冗余时间目前主要依人工经验设置，对于列车在沿途各站发生晚点给旅客造成的影响考虑不全面，因此还需研究更精细化的冗余时间布局方法。

国内外有许多学者已对冗余时间布局进行了研究。Cacchiani等[1]通过拉格朗日松弛算法，改进并实现了提升非周期性列车运行图轻鲁棒性的方法。Jovanović等[2]固定列车区间运行时分和停站作业时分，将列车间隔冗余时间优化分配抽象为背包问题。Andersson等[3]提出了混合整数线性规划模型进行优化。胡思继等[4]建立排队论模型，计算出必要平均列车运行图冗余时间。宗俊雅等[5]绘制连带晚点与平均列车间隔冗余时间取值关系曲线，通过寻找曲线变缓点确定冗余时间的合理取值。孙焰等[6]将单线区段运行图抽象成工序图，推算晚点概率计算必要冗余时间。孟令云[7]建立下层仿真补偿上层计算的双层模型优化冗余。蒋沐弘等[8]通过压缩运行图，建立冗余时间优化背包问题模型并求解。

然而在既有研究中，以优化客运服务质量为主要目标的研究尚不充分。针对既有研究的不足以及现场人工经验的局限，将客流数据纳入影响冗余时间布局的因素中，建立以旅客到达晚点总期望最小为目标的冗余时间布局优化模型，提出考虑冗余时间的列车晚点概率密度函数推算方法，以客流数据为权重，减小到达晚点时间加权期望，形成高速铁路列车运行图冗余时间布局优化方法。

1 模型构建

1.1 列车运行图网络计划模型与问题描述

设某个区段包含的车站数量为m，则区间数量为m-1，区段中包含的下行方向区间运行作业数量为n。若将列车在区间运行作业视为一项任务，用wj表示第j项任务，j=1，2，…，n；表示列车从车站驶入区间的时刻，即wj的开始时刻；表示列车从区间驶入下一站的时刻，即wj的结束时刻；tj表示wj的最小标准工时，包括区间纯运行时分和起停车附加时分，s；表示wj的计划工时，s，那么列车运行图就对应为一个包含有n个任务的网络计划。运行图与网络计划图对应关系示意图如图1 所示，图1a 是一包含4 个车站3 个区间的下行列车运行图，图1b 是用单代号网络计划图对其进行的表示。用(wi，wj)表示存在搭接关系约束的任务对，其基本搭接关系有4种[9]：①完成到开始(FS)关系；②开始到开始(SS)关系；③完成到完成(FF)关系；④开始到完成(SF)关系。列车最小停站作业时间和最小间隔时间约束条件均可用任务搭接关系来表示。

图1 运行图与网络计划图对应关系示意图Fig.1 The mapping from the train working diagram to the active-on-node network

设为列车最小停站作业时间，s；按作业类型对列车最小间隔时间进行划分，得到列车最小间隔时间符号含义如表1 所示。图1b中w1与w4均从A站始发，应满足列车最小出发间隔时间约束，对应SS 型搭接关系约束：w1到B站停站作业，w4在B站通过，应满足列车最小到通间隔时间约束，对应FF 型搭接关系约束：w4通过B站后w5立即开始，对应FS型搭接关系约束：w2到达C站停站作业后w3开始，应满足最小停站作业时间约束，对应FS型搭接关系约束，

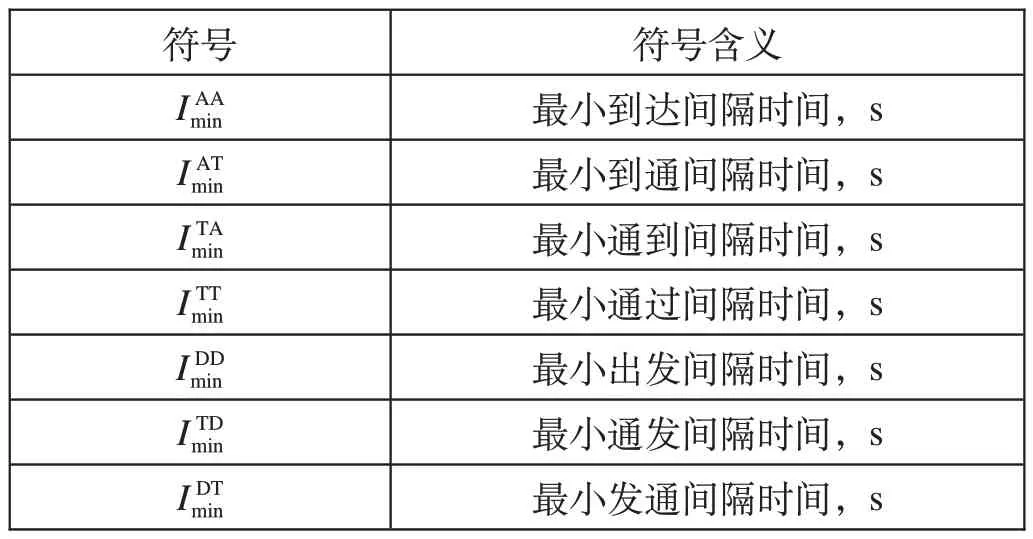
表1 列车最小间隔时间符号含义Tab.1 The meaning of the train minimum headway symbols

由于我国大部分铁路线路，尤其是高速铁路均是双线运营，正常条件下，上下行列车区间运行互不影响，因此可研究双线区段单方向运行图冗余时间布局，对于另一方向也同样适用。在网络计划中，如果不存在任何任务可以进行局部左移操作，则称此调度计划为半积极调度计划[10]。定义在固定开行顺序下，将运行图中各项运行任务，调整为其最早可能开始的时间，使其成为半积极调度计划，此过程称为运行图的“推线”。特别的，当运行图中各项任务的工时按运行标尺推线时，此过程称为运行图的“刚化”，刚化后的运行图称为刚性列车运行图，刚化后较原始运行图节省出的时间称为总冗余时间。

冗余时间布局优化问题求解思路是先将原始列车运行图进行刚化，再通过对各任务的开始、结束时刻进行局部右移，将总冗余时间重新“撒点”到运行图中，降低晚点概率，最终得到旅客到达晚点总时间期望值最小的冗余时间优化布局方案。

1.2 考虑冗余时间的列车晚点概率分布计算方法

列车实际发生的晚点可能是受初始晚点、连带晚点和冗余时间共同作用的结果。其中初始晚点是受随机干扰产生的，可作为独立的随机变量研究其概率分布，而连带晚点需考虑晚点传播因素，因此列车实际晚点往往服从的是两者在一定冗余时间下的联合概率分布。

1.2.1 列车初始晚点的概率分布

在实际运行过程中，随机干扰因素既可能发生在列车区间运行作业过程，也可能发生在列车停站办客作业过程。本模型的目标函数只关注列车到达晚点时间，针对区间运行作业添加冗余时间，本质是右移列车的到达时刻，能够直接起到吸收到达晚点作用。针对停站作业添加冗余时间，本质是右移列车的出发时刻，但由于列车不能早于计划时刻出发，故其对吸收列车到达晚点没有直接作用。停站干扰视为车站对区间运行的干扰示意图如图2 所示。对于发生在停站办客作业过程中的干扰导致列车出发晚点，可将其视为车站对区间运行作业的干扰，如图2 情况a 表示列车在停站作业和区间运行无干扰下的理想情况，情况b 表示列车在停站作业和区间运行中均受到干扰，情况c 表示将情况b 中的停站作业干扰也视为区间运行作业干扰的一部分，这样就将2 个随机因素合并考虑。模型假设列车在车站的停站作业过程不会发生初始晚点，只在区间运行作业中受到随机干扰，因而只针对区间运行作业添加冗余时间。

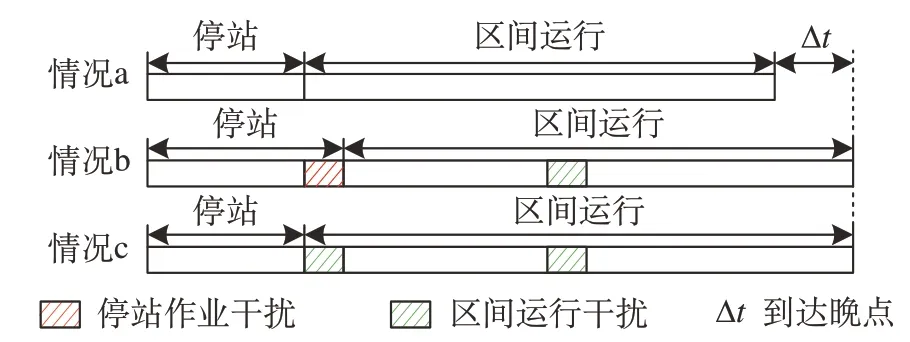
图2 停站干扰视为车站对区间运行的干扰示意图Fig.2 Schematic of regarding station disturbance as section disturbance

对于列车轻微初始晚点的概率分布，已有诸多学者做过研究，采用指数分布对其进行描述较为合理。对于任务wi，设随机变量Ξi为其运行初始晚点时长，s，可知Ξi服从指数分布E(qi)，其执行超时时长ξ的概率密度为

1.2.2 列车出发、到达晚点概率分布

（1）列车出发晚点概率密度。由于假设列车在车站的停站作业过程不发生初始晚点，因此列车出发晚点只可能受到2 个因素影响：①前车出发晚点导致连带晚点；②本列车在车站到达晚点导致连带晚点。列车实际出发晚点应取两种连带晚点的最大值。

对于任意wk，设有SS 型搭接关系的任务对(wi，wk)，随机变量为wi开始的晚点时长，s，(ξ)为其概率密度函数；有FS 型搭接关系的任务对(wj，wk)，随机变量为wj结束的晚点时长，s，(ξ)为其概率密度函数。

式中：表示(wi，wk)的SS 型搭接关系约束的时距，s，根据列车作业类型从列车最小间隔时间中确定对应的值。

式中：λj，k表示wj结束与wk开始之间是否存在停站作业，是则为1，否则为0。

那么，列车出发晚点ξ的累积分布函数为

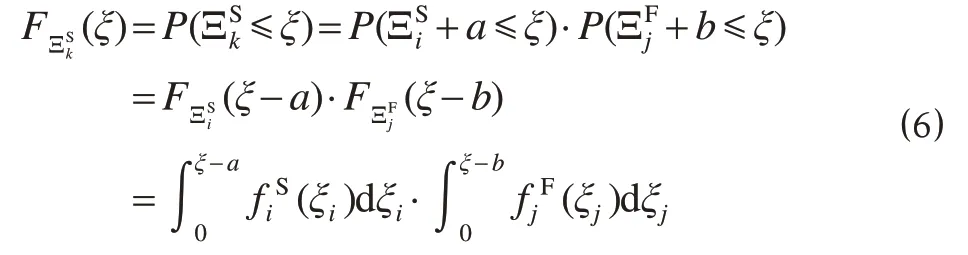
其概率密度函数为

（2）列车到达晚点概率密度。列车到达晚点可能受到3 个因素影响：①区间前车到达晚点导致连带到达晚点；②本列车在上一站出发晚点导致连带到达晚点；③本列车在区间运行作业中发生初始晚点。列车实际到达晚点应取因素①与因素②③之和的最大值。

对于任意wk，设有FF 搭接关系的任务对(wi，wk)，随机变量为wi结束的晚点时长，s，(ξ)为其概率密度函数；随机变量为wk开始的晚点时长，s，(ξ)为其概率密度函数；随机变量Ξk为wk执行超时时长，s，fk(ξ)为其概率密度函数。

式中：表示(wi，wk)的FF 型搭接关系约束的时距，s，根据列车作业类型从列车最小间隔时间中确定对应的值。

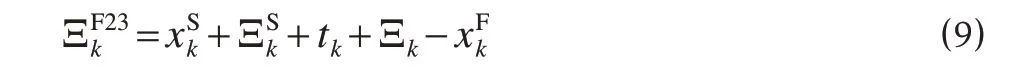
那么，列车到达晚点ξ的累积分布函数为

其概率密度函数为

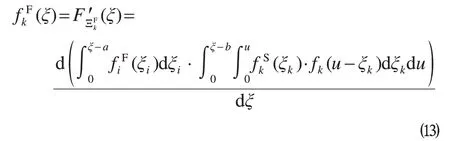
根据列车实绩运行数据可以计算出列车在区间运行超时服从指数分布的参数qi(i=1，2，…，n)，假设初始条件为所有列车在运行图中的首站始发正点，则可依次推算出，，，…，，等所有任务的开始和结束晚点概率分布。

1.3 数学模型

对于旅客而言，其重点关注的是列车作业在已经向公众公布了到发时刻信息的车站的履行情况，也就是列车在有客运业务车站的正晚点情况[2]，且旅客往往根据到达时刻安排后续计划，所以相较于列车出发晚点和通过晚点，到达晚点对旅客造成的时间成本更加显著。因此高速铁路列车运行图冗余时间优化模型以旅客到达晚点总时间期望最小为目标，则目标函数表示为

式中：Ei为所有列车在车站i到达晚点总时间期望值，采用公式⒂计算；ωi为车站i到达晚点总时间权重，采用公式⒃计算，含义为在车站i下车旅客占所有旅客数量的比值。

式中：为所有在i站结束的任务集合；di为在车站i下车旅客人数，人。

模型具有以下约束条件。

（1）单任务冗余时间约束。运行时分冗余设置过长可能会导致列车早点，若追踪运行的前车未出清进站进路，后车驾驶员会提前减速，在紧急情况下反而加大操作失误的概率，存在安全隐患，故对于任意一项区间运行作业，其冗余时间应存在上限约束。

式中：α为单个任务最大冗余比例；TW为最小标准工时向量，TW=(t1，t2，...，tn)T。

（2）旅行时间与运行图总冗余时间约束。列车的旅行时间不可过长，且冗余时间重新布局后的弹性运行图最后一列车终到时间不应超过原始运行图最后一列车终到时间。

式中：β为单列车旅行时间最大冗余比例；，TiTravel分别为列车i的终到时刻，始发时刻，最小旅行时间，s。

式中：T为运行图中第一列车始发到最后一列车终到的总时长，s。

（3）区间最小运行时间约束。列车在区间运行时分应不小于运行标尺，当在区间始端站或在末端站有停站作业时，还应包含对应的起停车附加时分。

（4）列车最小间隔时间约束。利用任务间的SS 搭接关系或FF 搭接关系表达列车最小间隔时间约束。对于存在SS 或FF 搭接关系的任务对(wi，wj)有

（5）最小停站时分约束。有FS 搭接关系的任务对(wi，wj)，wi结束与wj开始所在的车站相同。若列车在该站存在停站作业，任务对应满足最小停站时分约束，反之若列车在该站通过，则任务对FS搭接关系时距约束为0。

1.4 求解算法

模型在求解时，设置合适的时间粒度作为添加冗余时间的最小单位，并基于该粒度采用贪心算法进行求解。

在满足列车间隔条件且不超过单任务冗余时间上限条件下，若添加的冗余时间不会使运行图中最后一列车的终到时间推迟，则该冗余时间称为自由冗余时间，否则称为关键冗余时间。由于列车跨线或列车间存在速差和越行关系，刚性运行图中仍可能存在自由冗余时间，自由冗余存在形式如图3 所示。图3a中由于列车②在B站下线，则即使向任务2添加最多冗余时间，也不会影响任务5 的完成时间，即运行图总完成时间不变，因此为自由冗余时间。同理，图3b 由于列车①与列车②之间存在速差，且在B站被列车②越行，则向任务3、任务5的运行时分中添加冗余时间，也不会导致运行图总完成时间(任务6 的完成时间)推迟，因此此处的冗余时间也属于自由冗余时间。

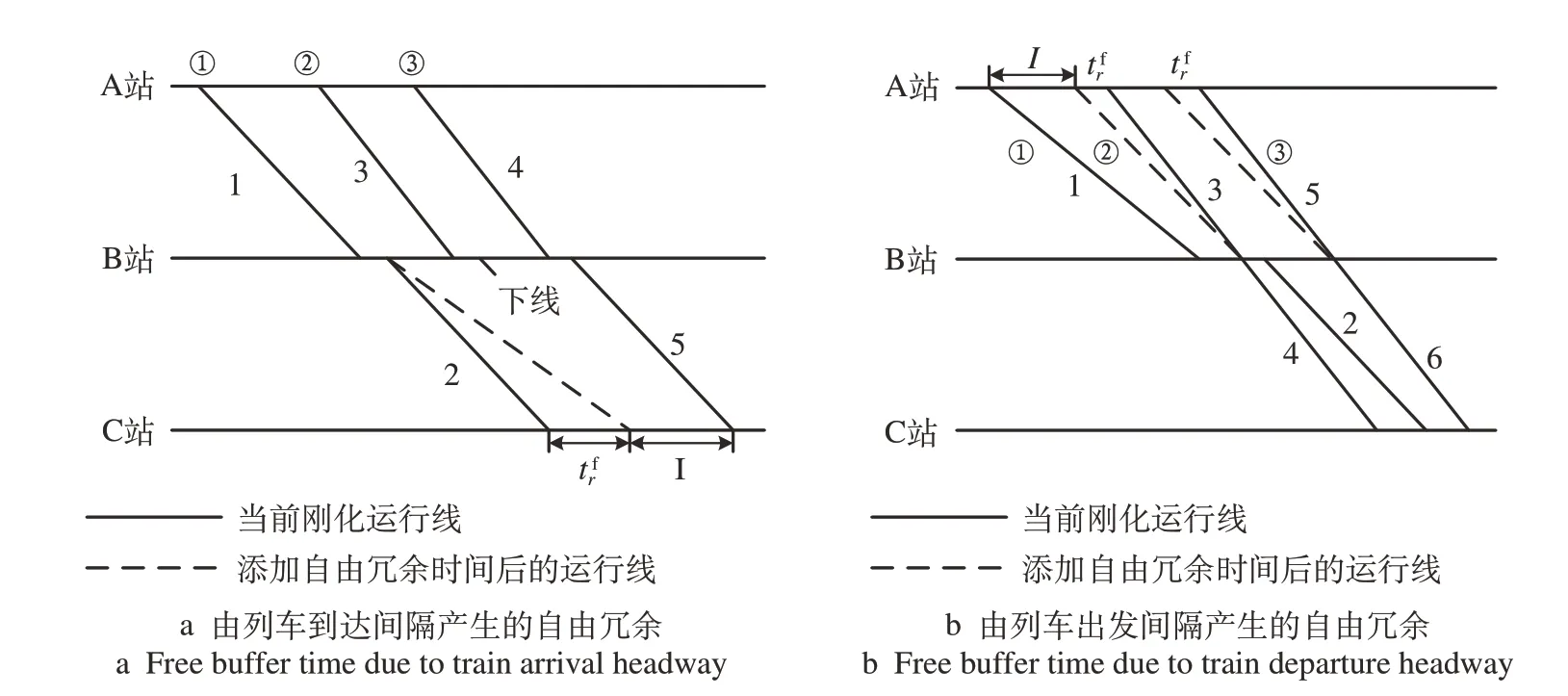
图3 自由冗余存在形式Fig.3 Forms of free buffer time

将总冗余时间看作可以使用的时间资源，添加自由冗余时间则可在不消耗时间资源的情况下，降低晚点期望值。由上述分析可得，冗余时间布局优化总是应优先考虑添加自由冗余时间。对于关键冗余时间，设计贪心算法，将计算每项任务在当前状态下添加一单位关键冗余时间后使目标函数减小的幅度作为价值函数，选择价值最大的任务添加关键冗余时间。

式中：z′为当前状态下目标函数值；zj为向任务wj添加一单位冗余时间后的目标函数值；svj为当前状态下选择任务wj添加冗余时间产生的价值。

每添加一单位关键冗余时间，可能使运行图中出现新的自由冗余时间，因此每次做出贪心决策后，仍需检查并添加当前状态下的可行自由冗余时间。算法步骤为：①刚化列车运行图，以刚性运行图为初始解；②更新当前状态，检查并添加可行自由冗余；③当前状态下，计算向每项任务添加一单位关键冗余产生的价值svj；④降序排列所有任务的价值，选择价值最大的任务添加一单位冗余时间；⑤判断是否满足运行图总冗余时间约束，是则转步骤②，否则转步骤⑥；⑥算法结束，将当前状态输出为优化后的列车运行图。

2 案例分析

2.1 基础数据

选取京沪高速铁路(北京南—上海虹桥)北京南—济南西区段下行列车运行图为研究对象，由于列车调度员通常以3 小时阶段计划下达调度命令，因此划定上午7：00—10：00 为时间范围。选取的案例列车运行图如图4所示。

图4 案例列车运行图Fig.4 Train working diagram of the train in the case

将京津线路所、津沪线路所并入廊坊—天津南区间，案例涉及5 个区间13 个车次，共61 个区间运行任务。根据历史客流数据得到各站客流权重，根据列车实绩运行数据统计得到各区间平均运行晚点，案例车站区间参数取值如表2 所示，由平均运行晚点可以确定任务超时概率分布的参数q。

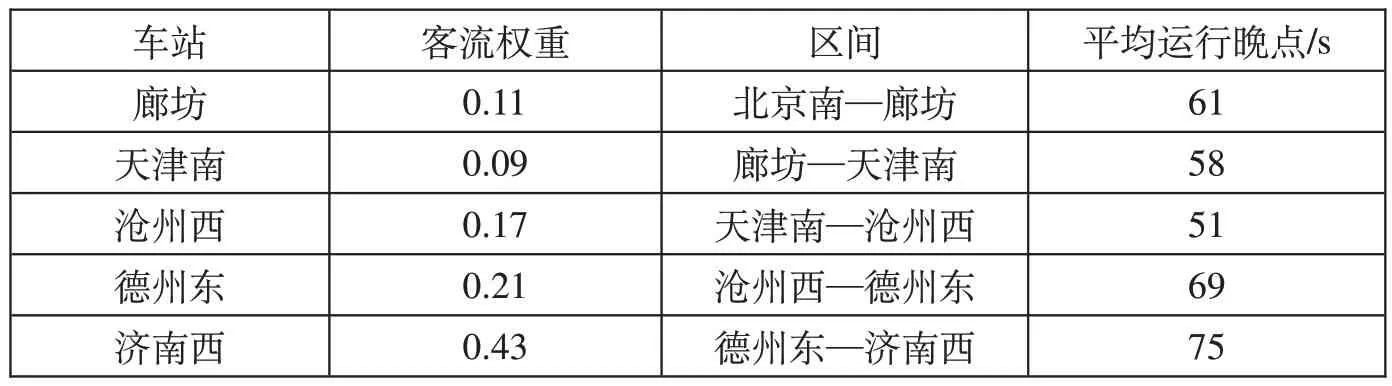
表2 案例车站区间参数取值Tab.2 Parameter values of stations and sections of the case

2.2 案例求解

设置单个任务最大冗余系数α=0.12，β=0.05，运行图完成总时间为3 h，即T=10 800(s)，冗余时间粒度为15 s，最小停站时间=120(s)，案例列车最小间隔时间取值如表3所示。

表3 案例列车最小间隔时间取值 sTab.3 Train minimum headway of the case

依照列车运行图中的运行线结构构建网络计划图，将对应参数代入模型，用贪心算法共决策70次，求解得出各区间运行过程添加的冗余时间，最终各列车在各区间运行添加冗余时间结果如表4所示。

表4 各列车在各区间运行添加冗余时间结果 sTab.4 Result of buffer time supplement in train sections

原始运行图计算目标函数值为33.96，优化后的运行图计算目标函数值为25.20，优化结果使旅客到达晚点总时间期望降低25.80%，进一步提升了高速铁路客运服务水平。

3 结束语

优化高速铁路列车运行图冗余时间布局，对于降低列车晚点率、保障运输组织秩序、提升运行图弹性、提高客运服务质量等有着重要意义。研究提出了考虑冗余时间的列车到达出发晚点概率密度函数计算方法，解决了如何在有限的冗余时间条件下向区间运行时分添加冗余时间的问题。以京沪高速铁路北京南—济南西区段为例进行计算，结果旅客到达晚点总时间期望值较原始运行图结果有明显优化。研究未考虑实际工作中调度员对列车开行顺序的调整，对于运行图弹性的提升，未来仍需要进一步结合运行图结构特点进行研究。