不规则三杆张拉整体结构的找形

2023-02-15刘贺平黄文杰宋健赖潇亮罗阿妮

哈尔滨工程大学学报 2023年2期

刘贺平，黄文杰，宋健，赖潇亮，罗阿妮

(哈尔滨工程大学机电工程学院，黑龙江哈尔滨 150001)

张拉整体结构通常以离散杆与连续的索构件组成，由于索构件在受压方向的模量为无限小，在结构不合理引起节点受力不平衡的情况下通常会产生坍缩的失稳形式，从而使结构整体无法自行维持一个常态形状[1]。在张拉整体结构的研究中，构型研究是结构研究中最基础的一步。当前构型分析中，优化分析是主要的研究方向，这些优化构型方法都是基于张拉整体结构静力学或动力学模型平衡准则的算法迭代进行数值求解，这一过程需要大量的计算推导构件变化后的稳定结构形态或基于节点及结构形态变化后以满足各构件的参数变化[2],或以动力学算法等进行满足构件变化及构件常数的非线性拟合规划找形[3-8]。基于此类数值迭代求解出来的构型通常很难获得结构参数与稳定构型的关系，从而无法做进一步的拓扑研究。

张拉整体结构的整体轻量化、自平衡等力学特性尤其适合刚度要求不敏感的机器人领域和仿生领域及空间展开结构领域等[9-11]。正是基于这样的特点，提出许多张拉整体机构。这些张拉整体机构，都是通过少数构件的长度变化，驱动整体运动，从而实现预期功能。在机构运动过程中，整体会连续变化其形状，而且任意时刻的形态都是稳定的，这既满足了机构可控性的要求，也为张拉整体结构的找形提供了一种思路。

本文基于规则3杆张拉整体单元，选择其3根斜索中的2根作为驱动构件，其长度主动控制变化，第3根斜索的长度随动变化，以此来获得稳定不规则3杆张拉整体结构。在分析过程中，以随动构件长度最小为确定稳定构型的标准，以结构整体节点受力的系统平衡矩阵的数值分析来进行稳定性的进一步检验，并利用仿真和实体模型来对此构型方法的正确性及相关算法的精度进行验证。

1 规则张拉整体单元

规则的3杆张拉整体单元结构如图1所示。图中，圆柱体代表杆构件、实线代表索构件。此结构包括3根杆和9条索，其中索构件可以分成3类，即上端面索、下端面索和斜索。上下端面由斜索连接并扭转一定角度。当上下端面直径相等时此结构整体外接于圆柱体，结构对称性好，上下端面的3根索都围成了正三角形，同类构件的长度和内力相同。如图1所示，连接上下端面节点的是杆构件和斜索构件，杆构件承受压力，斜索构件承受拉力，杆构件的内力有把2个端面之间距离撑大的趋势，而斜索构件的内力则是抵消这一趋势以保证结构轴向平衡，因此斜索对保持此张拉整体单元的稳定有直接影响。本文将通过斜索长度的变化对结构稳定性的影响来推导张拉整体单元的稳定条件。

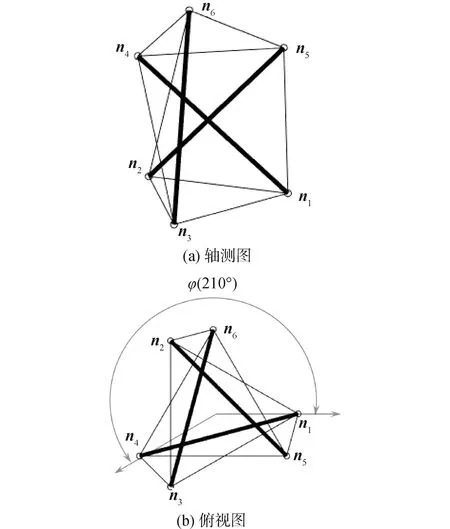
图1 规则3杆张拉整体单元Fig.1 Regular 3-bar tensegrity structure

斜索的2个端点分别位于上下端面。图1中，连于节点n1、n2和n3的斜索的另一个端点分别为n5、n6、n4。如果保持上下端面正三角形、杆构件与节点的连接关系、杆构件长度都不变，令2个端面始终平行，下端面固定不动，上端面绕着中心转动。当斜索长度最短时，此时结构的构型为稳定构型。依据这一思路，可以获得图1所示结构的稳定构型条件。当连接于节点n1、n2和n3的斜索另一个端点分别固定于n6、n4和n5时，也可以利用上述条件和方法，获得稳定构型。如果斜索构件和杆构件的两端节点重合，索杆结构布置不合理，结构也不能保持稳定。因此，规则3杆张拉整体单元只有2种稳定构型，这2种构型的区别主要在于斜索和节点的连接关系不同[12]。

同理，规则的p杆由p根杆构件和3p根索构件组成，三类索的数量均为p，其上下端面水平索都围成正p边形。令下端面节点ni(i=1,2，…,p)所连杆构件的另一个端点始终为np+i。依然保持高度、上下端面正多边形、杆构件与节点的连接关系、杆构件长度不变，各斜索长度相同令2个端面始终平行，下端面固定不动，上端面可以绕着中心转动。以n1节点为例，连接节点n1的杆构件的另一个端点为np+1，连于节点n1的斜索的另一个端点可以为np+1+j，其中j定义为分形参数，j=1，2，…，p-1，其余节点连接方式顺序类推。这样，规则的p杆单元就有p-1种稳定构型。图2为规则5杆张拉整体单元4种构型简图。

图2 规则5杆张拉整体单元4种分形Fig.2 Four fractals of regular 5-bar tensegrity element

2 规则张拉整体单元的稳定条件分析

2.1 数学模型

令R为规则张拉整体单元外接圆柱端面半径，h为其外接圆柱的高度，ra和rd分别为上下端面正多边形外接圆的半径。

设φ为同一根杆的2个端点在下端面上的投影与下端面形心连线的夹角(如图1所示)，这里称此角度为单元内转角。

规则p杆单元的下端面节点坐标为：

(1)

上端面节点坐标为：

(2)

p杆单元的杆连接矩阵为：

索连接矩阵为：

式中：Ip为p阶单位矩阵；j为前文所述的分形参数。

2.2 斜索长度分析

当稳定的张拉整体单元轴向承载时，其运动只有2种，即沿着轴线的整体高度的变化和绕着轴线的上下端面间的相对转动。撤除载荷后，此张拉整体单元将反向运动，恢复原来形态。也就是说，在张拉整体单元的大部分构件长度不变的条件下，在一定范围内改变其个别构件长度，稳定状态时的长度最小。下面根据这一思路来分析规则张拉整体单元的稳定条件。

图3 扭转连接斜索以保持结构稳定性Fig.3 Revolve the connected inclined cable to keep structural stability

令规则张拉整体单元的上下端面水平索和杆长度不变，只改变斜索长度。这里设斜索长度为|lik|(表示此斜索两端节点为ni和nk)，杆长度为|lib|(表示此杆件两端节点为ni和nb)。规则p杆张拉整体单元的第j种构型中，斜索长度可表示为：

|lik|=‖ni-nk‖=

(3)

设杆长为|lib|，结构的总体高度可表示为：

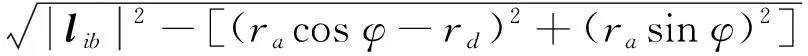
(4)

当i=1时，将式(4)代入式(3)：

(5)

式(5)的右侧表达式包含2部分，第1部分是常量，第2部分才是含有φ的变量，这里把式(5)中含有变量的部分提出：

(6)

当式(6)值最小时，斜索长度也达到最小。对式(6)求导，可得：

(7)

求解式(7)得：

(8)

由此推断，规则的p杆张拉整体单元，只要满足式(8)，即可稳定，这一结果与文献[13]的理论结果相同，也证明了此分析思路是正确的。

3 非规则三杆张拉整体结构的稳定构型解析

3.1 计算上底面三节点坐标

在2.2节，只改变规则张拉整体单元的某一类构件的长度，其余构件长度及受力特性不变，通过分析可知，变长度构件的长度最小时，此结构将处于稳定状态。下面将基于这样的特点，来探讨不规则3杆张拉整体结构的稳定构型确定方法。

本节依然令3杆张拉整体结构的杆构件、上下端面水平索长度都为定值，3根斜索中两条斜索的长度为自变量来确定第3条斜索长度，从而获得不规则的3杆张拉整体稳定构型。

图4所示为φ=7π/6时规则的3杆张拉整体单元。这里，令节点n1和n5之间连接的斜索为所求未知量。首先，根据下端面水平索的长度，可确定下端面3个节点n1、n2和n3的位置。由图4可知，连接节点n3的杆的另一个节点为n6，此杆长度|l36|为定值。固定于n6上的斜索的另一个节点为n2，此斜索的长度|l26|为自变量，也是需要提前给定的。以节点n3为球心，以|l36|为半径，绘制一个球面。以节点n2为圆心，以|l26|为半径，绘制另一个球面。这2个球面的交线为一空间圆弧(如图5所示)，那么n6节点一定位于此圆弧。

图4 节点与构件长度Fig.4 Nodes and lengths of members

图5 节点n6所在弧线Fig.5 The possible position arc of node n6

节点n6所处空间圆弧的圆心坐标可表示为：

(9)

该圆弧的半径为：

(10)

节点n6需要满足以下条件：

(11)

设n6节点坐标为[x6,y6,z6]T，将式(11)的第1个表达式代入式(9)，可得：

将式(9)、(10)代入式(11)的第2个表达式，可得：

(12)

利用上述方法也可确定n4节点所在圆弧(如图6所示)，此空间圆弧的圆心坐标可表示为：

图6 节点n4所在弧线Fig.6 The possible position arc of node n4

(13)

此圆弧的半径为：

(14)

节点n4需要满足以下条件：

(15)

将n4节点坐标设为[x4,y4,z4]T，将式(13)代入式(15)的第1个表达式：

将式(13)、(14)代入式(15)的第2个表达式：

由上述关系即可确定n4、n6节点坐标，具体确定步骤为，由方程组(11)选取n6节点坐标，再依据斜索长|l46|和方程组(15)确定n4节点坐标(如图7所示)：

图7 n6n4定距连接Fig.7 Distance connection of n6 and n4

|n6-n4|=l46

(16)

上端面:三节点坐标的之间的几何关系满足：

(17)

这样，依据节点n6和n4、构件长度|l56|、|l45|和|l25|，就可以确定节点n5的位置(如图8所示)。

图8 确定节点n5位置Fig.8 Determine the location of node n5

3.2 优化所求索长lx1

根据3.1节所述方法依据节点n6确定节点n4和n5坐标，这样就可以确定一个3杆张拉整体结构构型，但是这个构型未必是稳定的。依据第2节的分析，斜索长度|l15|必须为最小值时，结构才稳定。因此，稳定构型需要通过一个优化过程来实现。

此优化过程的自变量为节点n6于此空间弧线上的取值坐标：

结构稳定目标函数为：

min((x5-x1)2+(y5-y1)2+(z5-z1)2)

(18)

依据节点n6坐标获得的约束条件为：

(x6,y6,z6)∈

(19)

根据节点n4确定的约束条件为：

(x4,y4,z4)∈

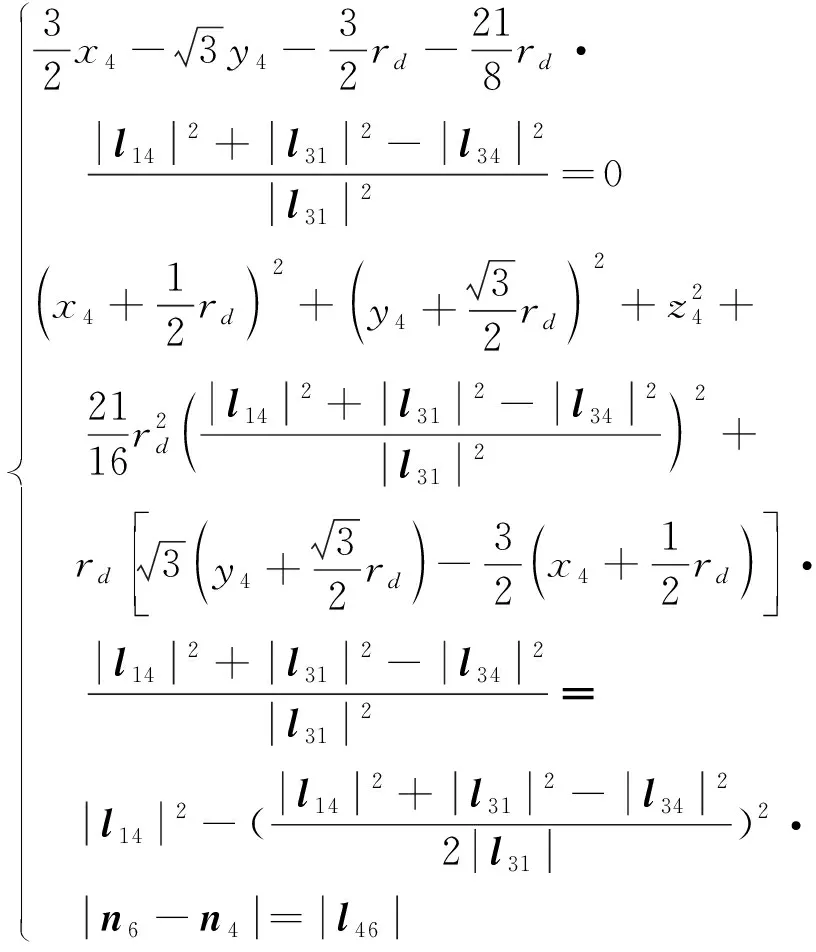
(20)

再根据各节点的位置关系和构件长度条件确定的约束条件为：

(21)

3.3 数值解算算法

根据上面的分析，可以获得斜索长|l15|最小时各节点坐标，由此进一步确定结构构型。此结构构型是否稳定，还需要进一步判断。

结构的平衡取决于节点的平衡，依据节点的力平衡可以建立结构整体的平衡方程。平衡方程的未知数为构件力密度。当结构处于自稳定状态时，此平衡方程的形式为：

At=0

(22)

式中：A为系统平衡矩阵；t为所有构件力密度所组成的力密度向量。

当平衡方程(22)存在一组非零解，即存在一组合适的构件力密度组合能够保持结构平衡时，此结构将能够处于自稳定状态。式(22)存在非零解，可以通过平衡矩阵来判断并求取。平衡矩阵可以通过下式的计算方法获得[13-14]：

(23)

式中：CS为索连接矩阵；CB为杆连接矩阵：

奇异值分解矩阵A，可得：

A=UVWT

(24)

式中：U为正交矩阵；WT为列正交酉阵，表示自应力模态；V为对角矩阵，为A的奇异值。如果λi和ti分别为平衡矩阵A的第i个奇异值和平衡方程(22)的第i个自应力模态向量，则：

(25)

若存在奇异值λi=0，则其对应的模态(特征向量)ti取值使得式(25)都为0，即平衡方程(22)存在非零解，表示此自应力模态下结构必然稳定。这样，结构自稳定的判断就转化为对系统平衡矩阵A的最小奇异值的判断。当奇异值最小值为0时，此结构的平衡方程有非零解，能够找到一组构件力密度使其保持平衡。

当利用算法数值求解时，A通常情况必然满秩，因此结构的稳定性的评价标准为A的最小奇异值是否接近于或等于0，通常取矩阵V的末位数值即A的最小奇异值作为数值迭代过程中结构稳定度的量化参考标准[15-16]。分析求解思路如下：

1)确定基本参数R、h及φ，计算规则3杆张拉整体单元的构件长度；

2)保持杆、水平索长度不变，确定主动斜索长度变化率；

3)计算2个主动斜索|l26|和|l34|的长度，确定节点n6轨迹；

4)确定n6轨迹的等分步长，计算n6坐标，再进一步计算n4和n5坐标，计算被动斜索|l15|长度；并取|l15|中的最小值所对应的坐标建立平衡方程。

5)建立平衡方程，计算平衡矩阵最小奇异值。

6)判断平衡矩阵最小奇异值，若小于预设值，即所得构型稳定，否则，取被动斜索|l15|最小值所对应的n6点所对应的相邻区间返回到第4步。

图9 变斜索结构稳态分析流程Fig.9 Steady state analysis process of variable inclined cable structure

3.4 数值算例

令ra=rd=70 mm，h=100 mm，初始单元内扭转角φ=210°。图10显示了3根斜索之间的长度关系。图10中，主动斜索|l26|、|l34|的长度与规则3杆张拉整体单元的斜索长度(此状态下3根斜索长度相等)，即初始态长度的比值为自变量，从动斜索lx1的长度与其初始长度的比值作为因变量。

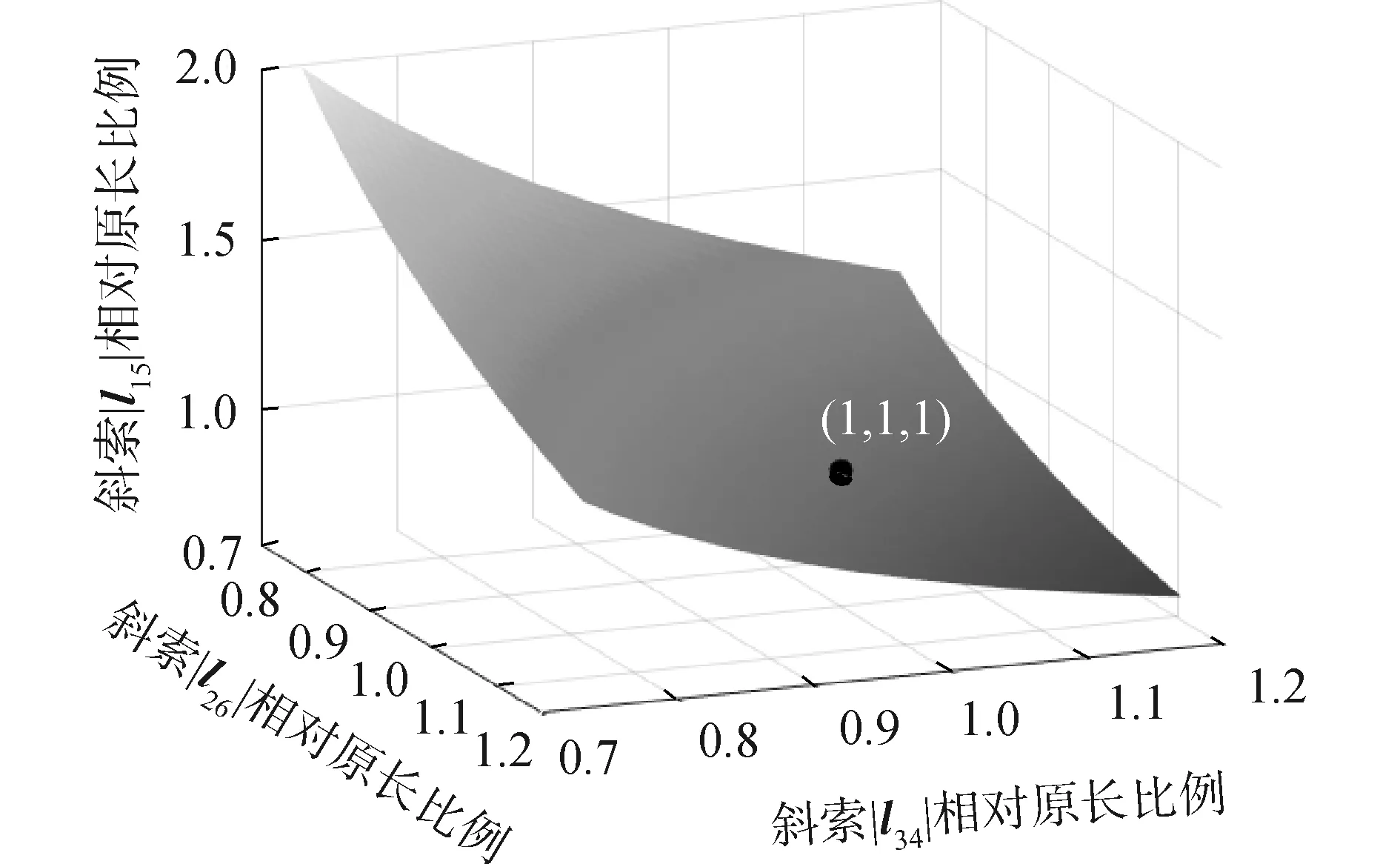
图10 斜索比例变化Fig.10 Scale change diagram of inclined cable

由图10可知，当2个横轴的数值为1时，曲线上对应点的竖轴数值也为1，即|l26|、|l34|长度相同，且为初始长度时，|l15|的长度为初始长度，也就是3个斜索的长度相同，这与规则3杆张拉整体单元的特性一样。这样的结果在一定程度上也验证了此算法的正确性。如图所示，随着|l26|长度的减小，|l15|的长度增大，即两者的变化趋势相反，|l34|和|l15|也有类似的关系。

下面将分析|l26|减小，同时|l34|同比例增加，且2个长度的变化量相等的情况下，求|l15|的变化情况。通过计算可知，当|l26|和|l34|在基于其原长的基础上变化超过20%时，计算得到的n5节点坐标将会低于XOY平面。从几何角度来分析，当结构处于稳定时，那么结构的每一个节点处的杆构件必然会处于由此节点的索构件围成的三棱柱内部；此计算结构的结构显然不稳定。所以，在此结构中2斜索的长度最大变化量约为初始长度的20%。图11显示了|l26|减小，同时|l34|同比例增加情况下|l15|的变化。由图可知，随着2个主动斜索变化量的增加，|l15|的长度也随之增加，但是|l15|的长度变化量较主动索要小得多。当2根主动索的长度变化量为5%时，从动斜索的长度增加量约为0.5%，为主动索变化量的0.1倍；当主动索长度变化量为10%时，从动索长度变化量约为1.5%，为主动索的变化量的0.15；主动索长度变化量为15%时，从动索的长度增加量为3.2%，约为主动索变化量的0.21；当主动索的变化量超过20%，从动索长度变化量为5.8%，为主动索变化量的0.29，而此时结构也将处于失稳临界状态。