尾流激励下功能梯度叶片动力学行为研究

2023-02-15王鑫鑫叶天贵靳国永刘志刚

哈尔滨工程大学学报 2023年2期

王鑫鑫，叶天贵，靳国永，刘志刚

(哈尔滨工程大学动力与能源工程学院，黑龙江哈尔滨 150001)

叶片作为燃气轮机的关键部件，其动力学性能直接影响着燃气轮机运行的安全性和稳定性。在实际运行中，由于叶片处于高速旋转的工作状态，不仅承受着强大的离心力载荷，而且需要抵抗高强度的气流压力，甚至涡轮叶片还会经受极大的热载荷，工作环境十分苛刻。开展叶片动力学特性分析，掌握叶片的动力学性能具有重要理论价值和工程指导意义。

目前，工程中常用于求解旋转叶片振动特性的方法有有限元法[1-3]、Galerkin法[4-5]、Ritz方法[6-7]等。牛宏伟等[8]通过有限元方法对航空发动机压气机转子叶片进行模态分析，揭示了动频曲线转向趋势和振型耦合规律。Sun等[9]建立了具有任意预置角的旋转薄板动力学模型，结合Galerkin法进行求解，并对旋转叶片的受迫响应进行了研究。李红影等[10]用壳模型模拟凸肩叶片，运用Galerkin方法分析了凸肩叶片的分岔特性。Sinha等[11]从薄壳理论出发并结合Ritz方法研究了旋转预扭叶片的振动特性。但是，旋转叶片并不是一个独立的个体，在工作过程中会受到气动载荷的影响，尤其是轴流式旋转机械，均匀静叶栅尾流会使下一级动叶受到周期性的尾流激振力，是导致动叶片疲劳破坏的主要因素[12]。初世明[13]考虑尾流激振力的作用，建立了柔性带冠旋转梁模型并对其非线性动力学特征展开研究。王迪[14]建立了多载荷作用下的旋转板模型，讨论了旋转叶片-机匣的碰摩问题。郑丽娟[15]与罗骁等[16-17]采用数值方法分析了尾流激励下的旋转叶片气动弹性行为。可以看出，许多学者针对各向同性材料叶片做了大量研究工作，已逐渐形成了较为系统的分析方法。

然而，随着机械结构工程的迅速发展，尤其在航空航天领域，人们对叶片强度、刚度、耐热、耐久性的要求越来越高，传统材料已经不能满足这些技术上要求。近年来，功能梯度材料作为一种兼具优良力学性能和热稳定性能的新型材料，不仅在一定程度上弥补了传统材料的不足之处，而且克服了多层复合材料层间应力集中、开胶以及断裂的缺点，应用越来越广泛。该材料在燃气轮机叶片制造领域具有重要的发展前景和实用价值，吸引了大量学者们的关注。目前针对旋转功能梯度叶片的研究主要集中在旋转梁[18-21]与旋转板[22-24]的自由振动，关于尾流激励下具有任意预置角的旋转功能梯度叶片动力学特性的研究较为少见，同时材料在空间上的连续梯度分布也对该类结构的动力学分析带来了新的挑战。

本文以多项正弦谐波叠加形式的尾流激振力作为气动载荷，基于经典板理论建立了具有任意预置角的旋转功能梯度叶片模型，通过罚函数将叶片的边界条件转化为边界势能的形式，以改进Fourier级数作为试函数表征叶片振动位移场。因此，本文利用Ritz方法对旋转叶片动力学行为进行求解时边界条件可以任意设置，且可根据实际工作选取合适的试函数以简化运算，更有利于建立统一的求解方法。

1 模型与方法

1.1 模型的建立

如图1所示，本文将具有任意预置角的旋转功能梯度叶片简化为一边固支在刚性轮毂上的板模型。

图1 旋转功能梯度叶片模型Fig.1 The model of the functionally graded blade

其中，X-Y-Z为主体坐标系，x′-y′-z′为旋转坐标系，x-y-z为局部坐标系，刚性轮毂的半径为R，带动叶片以Θ的角速度进行旋转，叶片长l宽b厚h，在刚性轮毂上的预置角为θ。

假设叶片的材料组分按照Voigt模型沿厚度方向连续过渡，则杨氏模量和密度可表示为:

(1)

式中：下标c与m分别代表上层的陶瓷组分与下层的金属组分，由于2种材料的泊松比μ相差无几，因此将泊松比设为常数。

叶片振动位移场可表示为：

(2)

几何方程为：

(3)

为简便起见，简化式(3)中的偏导数表达形式，例如εx将表示为εx=ux-zwxx。

物理方程为：

(4)

根据势能的定义，叶片弯曲势能Us表达式为：

(5)

罚函数方法引入的边界弹簧势能Up可表示为：

(6)

式中：k代表支撑弹簧刚度；K代表旋转弹簧刚度；上标u、v、w代表约束形变位移的方向。

旋转引起的离心力使得板结构内部产生特定的应力场，一般而言，薄板结构厚度方向尺寸远小于其余2个方向尺寸。为了简便起见，此处仅考虑x、y方向的离心应力分量，因此叶片旋转所产生的附加离心力势能Uc为[23]：

(7)

式中：χx与χy分别代表离心应力沿叶片x、y方向的分量：

图2为叶片俯视图与侧视图，其中α是在时间t内旋转过的角度，A是叶片上一点。设A在旋转坐标系内的位置为(x′,y′,z′)，在主体坐标系内的位置为(X,Y,Z)，在局部坐标系内的位置为(x,y,z)，通过A点可建立起3组坐标系之间的关系：

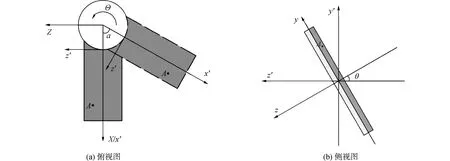
图2 旋转功能梯度叶片俯视图与侧视图Fig.2 Top and side views of the functionally graded blade

(8)

同样可以得到：

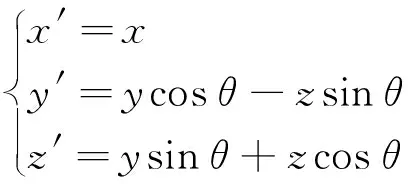
(9)

考虑到功能梯度叶片在旋转过程中的位移变形U、V、W，对式(9)进行修正：

(10)

由式(8)、(10)可以得到主体坐标系X-Y-Z中旋转梯度叶片上任意一点A的位置表达式：

(11)

由式(11)可得叶片上A点的速度表达式：

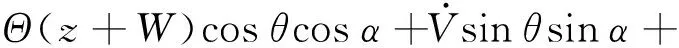
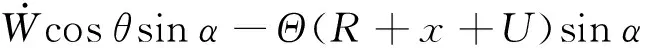
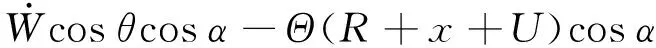
(12)

旋转功能梯度叶片的动能可表示为：

(13)

将式(2)与式(12)代入式(13),可以得到动能T的具体表达式：

Θ2w2cos2θ-2zΘ2wywsinθcosθ-2zΘ2uwx+

(14)

对于轴流式旋转机械来说，由于上游叶片尾缘和附面层的影响，引起导流叶栅出口气流速度发生亏损，从而形成尾流，同时因为上游叶片与下游叶片间的相对转动，使得上游尾流具有周期性激振效应[16]。如图3所示。

图3 尾流激振力示意Fig.3 The model of trail excitation

θ′为上游静叶的预置角，假设该角度为定值30°；Fq为尾流激振力，可将其表示为多项正弦谐波叠加的形式[13]：

Fq=F0+F1sin(nΘt)+

F2sin(2nΘt)+…+Fksin(knΘt)

(15)

式中：Fq是以时间为自变量的周期函数；F0为一常值，与时间t无关；Fk为第k次谐波分量的幅值，在得知具体的Fq后，Fk可以通过傅里叶级数展开得到[12]；Θ为叶片旋转角速度；n为上级静叶数目，决定尾流激振力的基频。

由线性叠加原理可知，旋转叶片在尾流激振力下总的响应等效于各激振力谐波单独作用下响应的叠加。本文取第k次谐波进行分析，并只考虑垂直于叶片表面的尾流激振力。根据图3中的几何关系，可以得到垂直于叶片表面的第k次尾流激振力Fkτ的大小为：

(16)

则尾流激振力对叶片做功为：

(17)

1.2 位移试函数的选取

在本文方法中，构造适当的位移试函数是至关重要的。为克服传统Fourier级数的弊端，本文引入改进Fourier级数来描述叶片的位移[25-26]，具体形式为：

式中：λlm=mπ/l，λbn=nπ/b；A、B、C是未知系数；M、N代表截断级数。

在位移试函数中，双重余弦项为位移主体项，ηi、ηj、ξi、ξj为辅助函数，其目的是为了保证容许函数在所有边界点上连续可导，因此这些辅助函数的构造形式并不唯一。为了简化后续的数学推导过程，构造辅助函数：

其中i=j=1, 2, 3, 4。

1.3 Ritz求解过程

旋转功能梯度板的能量泛函可以表示为：

L=T-U+W0

(18)

式中：T为系统的总动能；U代表系统的总势能；W0代表尾流激振力做功。

令能量泛函对未知系数求偏导为零，可以得到旋转功能梯度叶片的振动微分方程：

(19)

式中：M为质量阵；C为阻尼阵；K为刚度阵；q为未知系数组成的列向量；F为广义力向量。当外力功为零时，式(19)退化为求解自由振动的微分方程。

在处理式(19)的特征值问题时，可将正弦形式的激振力视为exp(ikΘt)形式简谐力的虚部。由于尾流激振力是与叶片转速Θ有关的，因此通过扫频求解可以得到不同转速下的多组未知系数q。为反映旋转叶片整体的振动情况，引入均方根速度：

(20)

式中S为叶片的表面积。

计算结果表示为均方振速级Lv：

Lv=20lg(V/Vref)

(21)

其中Vref=10-9m/s。

本文采用复合杨氏模量的形式将结构阻尼包括在叶片模型中，即E^=E(z)(1+βi),其中β为结构阻尼系数，在本文中取β=0.01。

2 计算结果及分析

2.1 收敛性分析

由于本文采用基于改进Fourier级数的Ritz法分析叶片的振动特性，因此该方法的计算速度与精度和截断级数M、N的选取有关。因而，通过收敛性分析来确定所需的截断级数对后文的分析至关重要。本算例中：杨氏模量E=221 GPa，密度ρ=7 850 kg/m3，泊松比μ=0.3，叶片尺寸180 mm×85 mm×2 mm，边界弹簧刚度、刚性轮毂半径R、轮毂转速Θ与预置角θ均设为0。表1给出了不同截断级数下叶片的前8阶固有频率，此处没有考虑刚体模态，且本文计算结果均保留5位有效数字。从表1中可以看出，随着截断级数的增加，各阶固有频率逐渐收敛。综合考虑求解精度与计算速度，在后续的分析中令M=N=12。

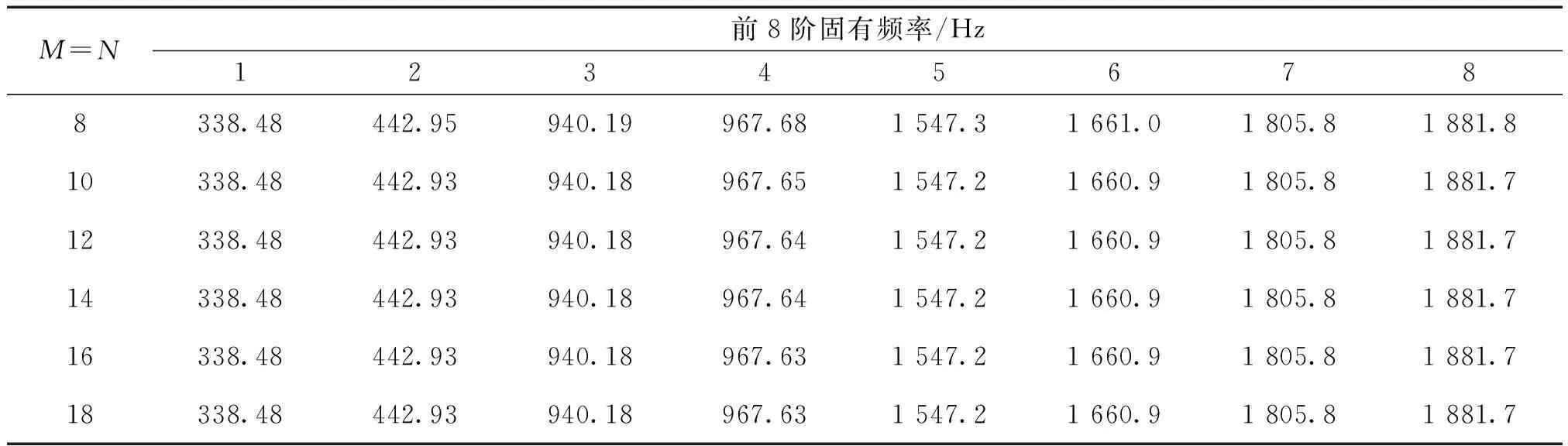
表1 不同截断级数下叶片前8阶固有频率Table 1 The first eight natural frequencies of the blade with respect to truncated numbers

此外，本文采用罚函数处理叶片的边界条件，因此弹簧刚度的取值会直接影响求解结果。为准确模拟不同的边界条件，定义刚度参数Γm，令k=K=10ΓmN/m，即假设支撑弹簧刚度k与旋转弹簧刚度K同等变化，其他参数与表1算例相同。图4展示了前3阶固有频率随Γm的变化趋势，从图中可以直观看出：在区域Ⅰ与区域Ⅱ内，各阶固有频率保持不变，分别对应自由边界区间与固支边界区间；在中间区域各阶频率会随着Γm迅速增大，该区域对应弹性边界区间。在后续的分析中，本文选择Γm=0与Γm=12分别作为自由边界值与固支边界值。

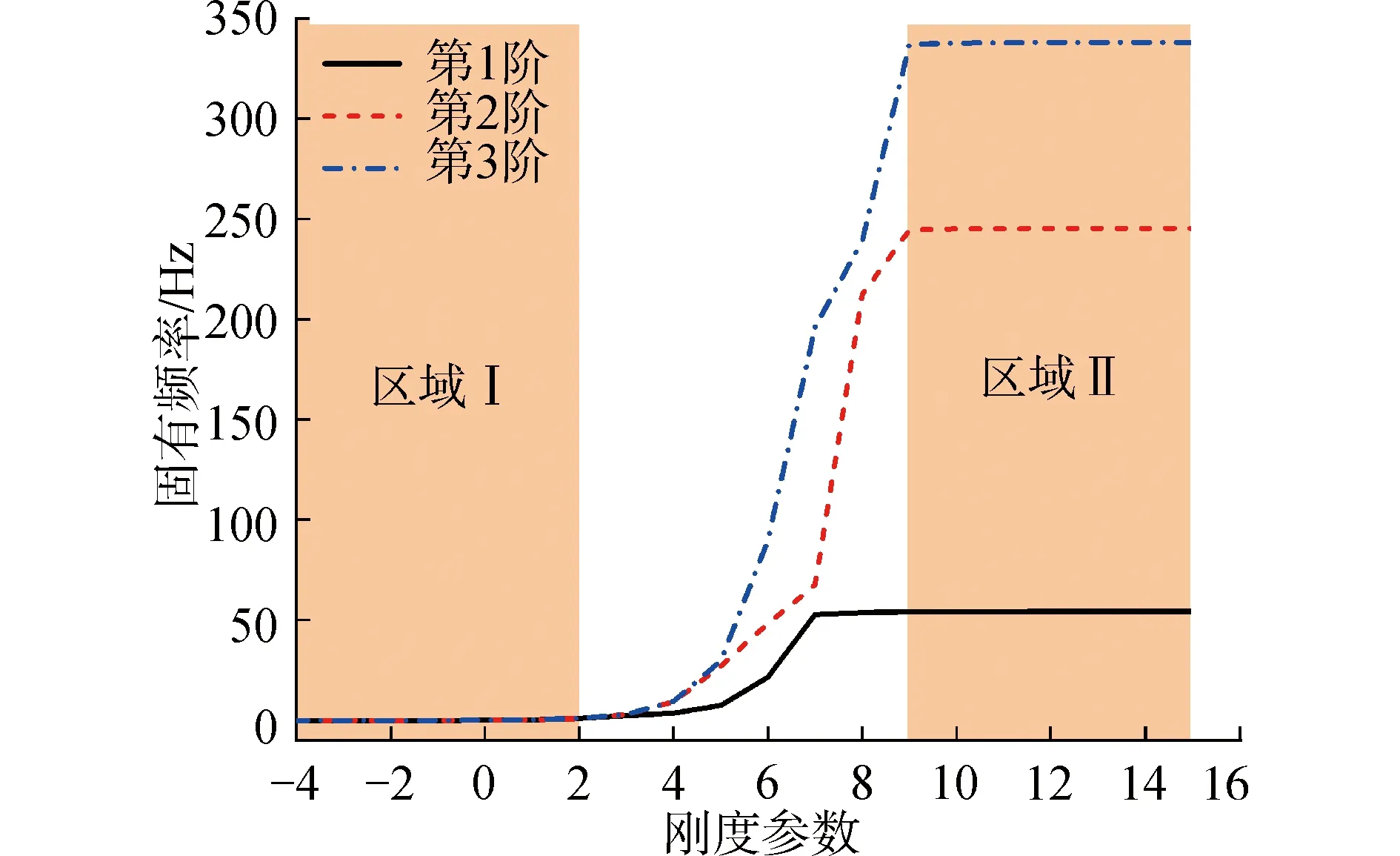
图4 边界约束弹簧的收敛性Fig.4 Convergence of Γm for mechanical boundaries

2.2 正确性验证

为验证本文方法的正确性，表2给出了不同预置角下旋转叶片的前5阶固有频率，同时列出了文献[9]中的部分计算结果。在该算例中：杨氏模量E=221 GPa，密度ρ=7 850 kg/m3，泊松比μ=0.3，刚性轮毂半径R=0.25 m，叶片尺寸180 mm×85 mm×2 mm，轮毂速度Θ=300π rad/s。

表2 不同预置角下旋转叶片前5阶固有频率Table 2 The first five natural frequencies of rotating blade with respect to the presetting angle

通过表2数据的纵向对比可以发现，随着预置角的增加，旋转叶片的各阶固有频率均有增加的趋势；通过横向对比可以看出，当截断级数取12时，无论在何种预置角下，本文方法计算的数据结果与文献[9]的数据能很好的吻合，从而验证了本方法计算旋转叶片固有频率的正确性。

2.3 动力学行为研究

假设叶片由上层的陶瓷氧化铝与下层的TC4钛合金组成，二者材料属性如表3所示。选取尾流激振力中的第k次谐波进行分析，假设n=1，叶片的尺寸为180 mm×85 mm×2 mm，刚性轮毂半径R=0.25 m。

表3 旋转功能梯度叶片的材料属性Table 3 Material properties of functionally graded blade

图5给出了不同尾流谐波下激振力幅值对旋转功能梯度叶片均方根速度响应的影响规律。其中，功能梯度指数P=0.5，预置角θ=60°。通过图中3组曲线可以看出，叶片速度响应随着尾流激振力幅值增大而增大，各阶共振峰也逐渐陡峭；同时通过纵向对比发现尾流激振力谐波的谐次越高，所激起的共振峰越多，且各阶共振峰对应的转速会逐渐向左移动。

图5 不同幅值激励力下叶片的速度响应曲线Fig.5 Effect of amplitudes of excitation force on velocity response curves of functionally graded blade

为探究激振力谐次k对旋转叶片振动特性的影响规律，作出不同功能梯度指数P下旋转叶片的坎贝尔图，如图6所示。可以发现，叶片各阶动频会随着转速的增加而增大。转速越高，叶片受到的离心力越大，使得叶片产生更大的附加拉伸变形，导致叶片抗弯刚度增加。同时可以看出，在该转速范围内，第1谐次尾流激振力频率与叶片动频没有交点，因此不会激起叶片共振。从k=2开始，不同谐次的激振力频率会与叶片动频相交于不同的点，理论上这些交点所对应的转速就是叶片的临界转速。尾流激振力的谐次越高，越容易与动频产生交点，同时导致各阶临界转速逐渐向左移动，图6所反映的现象与图5完美契合。同时，在实际工程中，由于旋转叶片上游的静叶数目n较多，导致尾流激振力的基频较高，因此即便是低谐次的尾流也易与叶片动频产生交点，导致叶片临界转速大多分布在低速区，因而在起动阶段需要保证发动机很快的通过该危险区域。

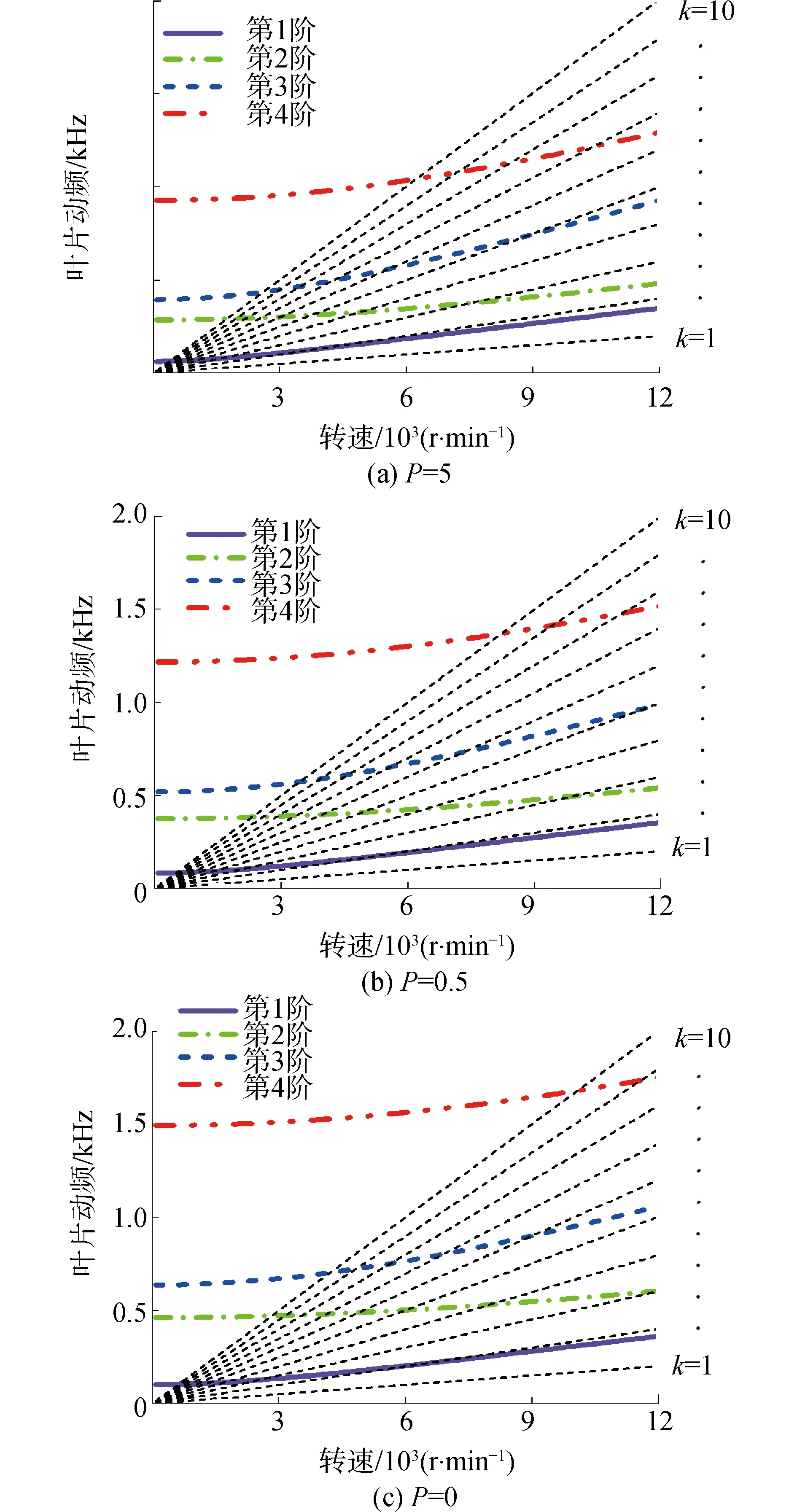
图6 功能梯度叶片坎贝尔图Fig.6 Campbell diagrams of functionally graded blade

同时通过图6的横向对比可以发现，当其他参数相同时，叶片各阶动频与各阶临界转速均会随着功能梯度指数P的增加而降低。为直观反映变化趋势，图7以尾流激振力第6次谐波分量为例，给出不同功能梯度指数P下旋转叶片均方根速度随转速的变化曲线。当功能梯度指数为0时，叶片可认为只含有陶瓷氧化铝，此时叶片的各阶固有频率最大。当功能梯度指数P增加时，TC4钛合金在总材料中所占比例增大，叶片材料属性的改变导致叶片各阶固有频率发生变化。因此在设计固定尺寸的转子叶片时，可通过改变叶片材料分布情况来调整叶片固有频率，使叶片的共振转速不落在发动机常用工作转速范围内。

图7 不同功能梯度指数下叶片的速度响应曲线Fig.7 Effect of different material parameters on velocity response curves of functionally graded blade

图8给出了不同激振力谐次k下轮毂半径R对旋转叶片振动特性的影响规律。其中功能梯度指数P=0.5，预置角θ=60°。通过纵向对比可以发现，k越大，轮毂半径R对低阶共振峰的影响越小。同时可以直观看出，在特定谐次的尾流激振力下，随着轮毂半径R的增大，旋转叶片各阶共振峰会向右移动，且频率阶次越高变化越明显。这是因为当转速相同时，旋转半径越大，叶片受到的离心力分量也越大，导致叶片的抗弯刚度显著增加，从而使旋转叶片各阶共振转速会向着较大的一方移动。同样，当叶片展弦比(l/b)、厚长比(h/l)等参数改变时也会出现类似的现象，这里不再给出曲线图。