基于修正辅助变量法的船舶操纵响应模型辨识
2023-02-15曾道辉蔡成涛
曾道辉, 蔡成涛,2,3
(1.哈尔滨工程大学 智能科学与工程学院,黑龙江 哈尔滨 150001; 2.船海装备智能化技术与应用教育部重点实验室,黑龙江 哈尔滨 150001; 3.电子政务建模仿真国家工程实验室,黑龙江 哈尔滨 150001)
随着船舶智能化和自主化水平的提升,使得船舶在操纵性能变化的动态环境和多任务场景约束下的安全高效航行更依赖于在线建立的船舶操纵运动模型。船舶操纵运动模型在用于辨识的结构方面,可具体分为分离型[1]、整体型[2]、响应型[3]和时间序列[4-5]多种模型结构形式。而船舶操纵响应模型作为船舶操纵运动模型中的一种,其中的操纵性指数物理意义明显,能够直观反映船舶的操纵性能,是一种描述船舶舵角与航向角映射关系的动态响应模型。通过对船舶操纵响应模型的在线辨识建模,不仅能够为船舶的自动舵和航向自适应控制器提供精确的数学描述,而且能预报船舶的未来航向以及通过辨识的操纵性指数实时反映船舶的操纵性能。因此,实现船舶操纵响应模型参数的在线辨识,对船舶的航向预报和航向控制有着重要意义。
为了辨识船舶操纵响应模型中的参数,目前已经有许多系统辨识方法用于船舶操纵响应模型的在线辨识中。文献[6]以一阶船舶操纵响应模型为辨识对象,设计了一种基于标准最小二乘法的在线参数辨识试验平台,结合实船试验数据验证了在线辨识试验平台设计的正确性和合理性。文献[7]通过引入P型学习率,提出了一种快速收敛迭代学习最小二乘算法,用于辨识船舶的一阶非线性响应模型和二阶非线性响应模型,文中仿真和水池实验均表明,该算法相比标准最小二乘法在收敛速度和辨识精度都有所提高。文献[8]针对船舶二阶非线性响应模型,利用多新息最小二乘法对其进行参数辨识,辨识结果表明该算法辨识的参数更接近真实值,能更准确地描述船舶运动的动态特性。文献[9]针对装载吊舱式推进器的无人水面艇,利用最小二乘法辨识了其一阶船舶操纵响应模型,对辨识模型进行回转试验的结果同实船回转试验结果的比对证明了辨识得到模型的正确性。文献[10]针对船舶实际航行中存在海洋环境扰动和数据欠激励的情况下,提出了一种满秩分解最小二乘算法对船舶一阶线性响应模型的参数进行辨识,辨识结果表明了该算法能抑参数发散,并能够获得更高的参数辨识精度。文献[11]对最小二乘支持向量机算法中的偏置项引入了惩戒因子进行了改进,大大改善了辨识模型的精度;文献[12]利用滚动时间窗内的数据实时辨识参数的策略,增强了对船舶操纵响应模型的参数跟踪能力;文献[13]针对最小二乘支持向量机引入自适应加权的策略进行改进,并结合实船试验验证了该方法的有效性。文献[14]将其应用于船舶的航向控制,增强了船舶航向保持精度、降低了航向调节时间和超调幅度;文献[15]从解析模型的角度出发,结合格雷码和精英选择的策略对参数进行非线性寻优,使得该算法在小样本数据情况下就可进行高效准确的辨识,极大地提升了辨识效率。文献[16]针对多新息扩展卡尔曼滤波算法引入了遗忘因子进行改进,有效较低了历史累积数据对参数辨识的影响,文中结合船模数据的辨识结果表明,该改进算法相比标准扩展卡尔曼滤波辨识方法在船舶操纵响应模型参数辨识方面更加精确。
上述的文献方法在模型参数辨识精度、收敛速度和参数实时跟踪性能上均有贡献,但都并未考虑受到有色噪声干扰的实际量测数据会给参数辨识带来有偏估计的影响。实际船舶航行过程中,由于海洋环境高频扰动和传感器测量噪声等因素,会使得辨识的船舶操纵性指数存在精度上的误差,这一缺陷给船舶的航向控制和预报都带来了一定的影响,因此如何快速无偏地辨识船舶的操纵性指数是实现船舶操纵响应模型在线辨识中的关键问题。
考虑到实际过程中,噪声对系统的影响是不可避免的。此时,要获得系统模型参数的一致无偏估计, 递推辅助变量最小二乘法(recursive instrumental variable least squares method, RIVLS)是一种有效的辨识方法。本文在RIVLS算法的基础上,结合动态滤波的思想对其进行改进,提出了一种递推修正辅助变量最小二乘法(recursive refined instrumental variable least squares method, RRIVLS)。该算法能够对实时观测得到的数据进行一次滤波预处理后,再结合辅助变量对模型参数进行辨识。辨识试验以二阶船舶操纵响应模型为辨识对象,在实船Z形试验数据的基础上,将递推修正辅助变量最小二乘法、辅助变量最小二乘法、增广最小二乘法(recursive extended least squares method, RELS)和标准最小二乘法(recursive least squares method, RLS)的辨识模型进行比较。
1 船舶操纵响应模型
船舶操纵响应模型是通过描述船舶航向角相对于舵角动态响应关系建立的模型。本文辨识的响应模型为二阶线性响应模型,其方程为:
(1)
式中:r为船舶艏摇角速度;δr为外界环境干扰力矩造成的等效压舵角;K为舵角增益系数;T1、T2和T3为时间常数。
考虑到艏摇角速度r不易通过传感器直接获取,因此对其利用航向角ψ前向差分得到:
(2)
式中h为采样周期。

(3)

(4)
根据方程转换法,令H=T1+T2,G=T1T2,同时结合式(2)~(4),对式(1)进行相应的变换,可得到如下的受控自回归模型(controlled auto-regressive, CAR):
r(k)=a1r(k-1)+a2r(k-2)+
b1δ(k-1)+b2δ(k-2)+c
(5)
式中:a1、a2、b1、b2和c为待辨识参数,与K、T1、T2、T3和δr的关系为:
(6)
式(5)的模型可以描述船舶在风浪不太大的环境下的船舶操纵运动特性,对其加入噪声干扰的影响,可得到如下的CAR模型:
r(k)=a1r(k-1)+a2r(k-2)+
b1δ(k-1)+b2δ(k-2)+c+e(k)
(7)
式中e(k)为船舶所受的有色噪声,将该有色噪声假设为自回归过程(AR模型),其模型的具体结构形式为:
(8)
式中:v(k)为均值为0的不相关随机白噪声;C(z-1)为单位后移算子z-1的多项式:
C(z-1)=1+c1z-1+c2z-2+…+cncz-nc
式中nc为噪声向量的阶数。
若当前采样的时刻为k,式(7)可改写为:
z(k)=φT(k)θ+e(k)
(9)
其中:
z(k)=r(k)
φ(k)=[r(k-1)r(k-2)δ(k-1)δ(k-2) 1]T
式(9)对应的系统矩阵形式为:
Zk=Φkθ+Ek
(10)
式中:
2 辅助变量最小二乘法的原理和改进
2.1 递推辅助变量最小二乘算法的原理
最小二乘算法是一种根据最小二乘准则,在参数空间寻找一组最优模型参数估计值用于拟合系统模型的参数辨识方法,即令系统测量的输出值与辨识模型输出值之间的误差平方和最小。式(10)的参数估计值的最小二乘解可写为:
(11)
观察式(11)最右侧的第2项可知,只有当该项的值依概率收敛为0时,即:
(12)

继续分析式(12),可变形为:
(13)
(14)

(15)

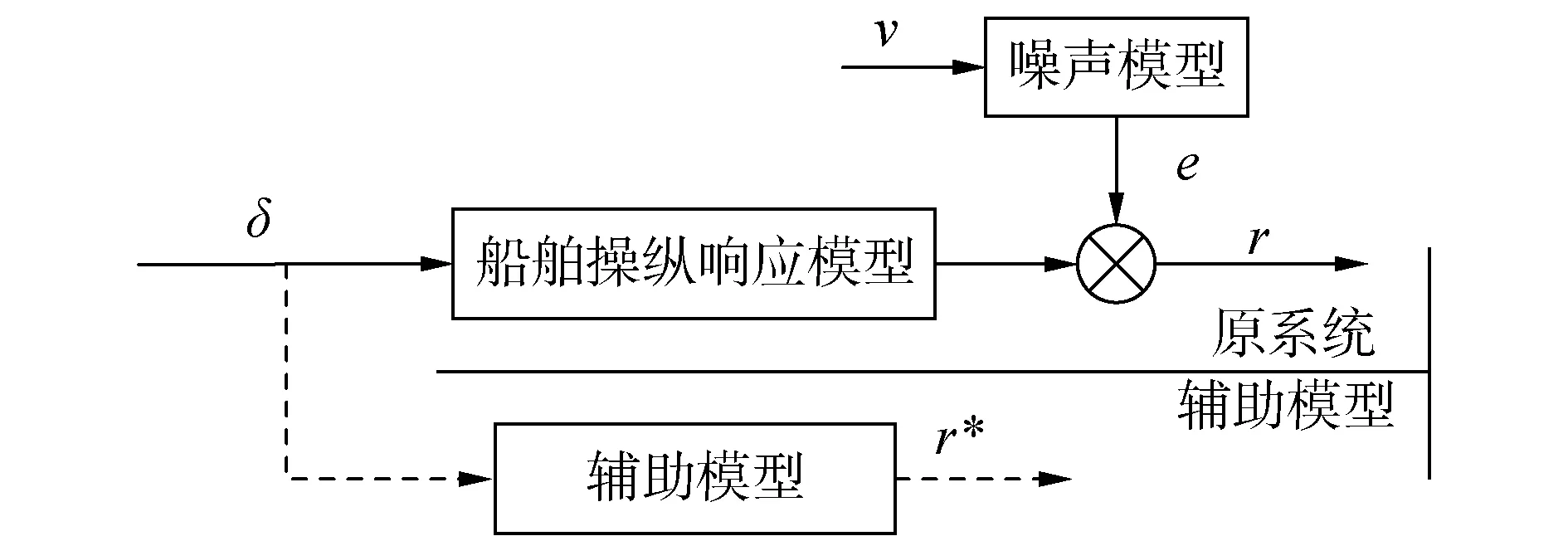
图1 辅助变量构建原理Fig.1 Diagram of instrumental variable construction

φ(k)=[r(k-1)r(k-2)δ(k-1)δ(k-2)1]T
(16)
φ*(k)=[r*(k-1)r*(k-2)δ(k-1)δ(k-2)1]T
(17)
K(k)=P(k-1)φ*(k)[1+φT(k)P(k-1)φ*(k)]-1
(18)
(19)
P(k)=[I-K(k)φT(k)]P(k-1)
(20)
(21)
(22)
2.2 递推辅助变量最小二乘算法的改进
A(z-1)r(k)=B(z-1)δ(k)+c+e(k)
(23)
其中:
(24)
如对式(23)两边同乘一个预滤波器F(z-1),可得:
A(z-1)rf(k)=B(z-1)δf(k)+cf+ef(k)
(25)
其中:
(26)
显然,若正确选择预滤波器F(z-1)可实现对式(8)中多项式C(z-1)的对消,从而改善有色噪声e(k)的统计特性。预滤波器F(z-1)的数学模型表示为:
F(z-1)e(k)=v(k)
(27)
式中:
F(z-1)=1+f1z-1+f2z-2+…+fnfz-nf
(28)
该滤波器是未知的、有限阶的线性滤波器。自回归有色噪声e(k)在预滤波器F(z-1)的作用下将会逐步白化,这在一定程度上能够降低系统的噪信比,提高自适应滤波器的递推精度。相比常规的辅助变量法,这种处理问题的方法称作修正的辅助变量法[17]。综上所述,从式(16)~(28),可以将递推修正辅助变量最小二乘法(RRIVLS)归纳成:
φ(k)=[r(k-1)r(k-2)δ(k-1)δ(k-2) 1]T
(29)
φf(k)=[rf(k-1)rf(k-2)δf(k-1)δf(k-2) 1]T
(30)

(31)
(32)
(33)
(34)
(35)
(36)
(37)
(38)
(39)
(40)
(41)

(42)
(43)
(44)
(45)
(46)
式(29)~(46)的递推过程表明,修正的辅助变量法的基本思想是先对观测得到的数据进行一次滤波预处理后,再结合辅助变量法对模型参数进行辨识。其中所用的滤波模型实际上是一种动态模型,在整个迭代过程中不断靠偏差信息来调整滤波器参数,使其逐步逼近于一个较好的滤波模型,从而改善噪声的统计特性。理论上如果滤波模型选择得合适,再经过迭代后便可对数据进行较好的白化处理,但是实际过程中的噪声过程复杂且充满不确定性,这使得数据白化处理的可靠性下降。因此RRIVLS算法在数据预滤波处理的基础上将其与原有的辅助变量法相结合,进一步提升参数辨识精度,实现对模型参数的无偏估计。需要注意的是,当滤波器阶数设置为nf=0,则F(z-1)=1,此时RRIVLS算法将退化为RIVLS算法。
3 试验验证
为验证RRIVLS对船舶操纵响应模型的参数辨识效果,在相对平稳的海况下,以本研究团队自主建造的科研试验船在海洋环境下进行10°/10°和20°/20°Z形试验。科研试验船的船型和主尺度参数分别如图2和表1所示。

图2 科研试验船Fig.2 Research vessel

表1 科研试验船的主尺度参数Table 1 Principal dimension parameters of research vessel
试验的采样序列长度为1 000,采样周期为0.2 s。Z形试验的数据曲线如图3所示,其中的艏摇角速度通过式(2)差分得到。注意到图3中Z形试验数据中的艏摇角速度在某些时刻出现了抖动,这是由于试验的航向角数据是在真实海洋环境下进行采集,所采集的航向角数据不可避免的会受到海洋环境的高频扰动和传感器测量噪声的影响,因此艏摇角速度的差分过程会将该类噪声进一步放大,从而致使艏摇角速度出现抖动,这也是式(7)中所提及的有色噪声,受到有色噪声干扰的实际量测数据会给参数辨识带来有偏估计的影响。因此,本文所提出的RRIVLS算法针对受到有色噪声干扰的艏摇角速度数据进行辨识建模,力图获得参数的无偏估计。

图3 Z形试验数据曲线Fig.3 Zigzag test data curve
3.1 船舶操纵响应模型参数辨识结果及分析
利用RRIVLS(nf=1)的式(29)~(46)结合上述的Z形试验数据对式(7)中的模型参数进行辨识,并将其与RIVLS、RELS和RLS算法进行比对,得到的参数辨识曲线图分别如图4、图5所示。各算法的初始设置情况如下所示:

图4 基于10°/10°Z形试验数据的参数辨识曲线Fig.4 Parameter identification curve based on 10°/10° zigzag test


图5 基于20°/20°Z形试验数据的参数辨识曲线Fig.5 Parameter identification curve based on 20°/20° zigzag test
由图4和图5可知,在10°/10°Z形试验中,四种算法在递推至400次左右时,所辨识的参数均已呈现收敛趋势;在20°/20°Z形试验中,RRIVLS和RIVLS辨识的参数在递推至200次左右均呈现收敛趋势,而RELS算法辨识的参数a1以及RLS算法辨识的参数b1和b2并未呈现收敛趋势,这是因为RLS算法由于自身的固有缺陷,容易受有色噪声的影响,致使对参数的辨识过程逐步偏离真值,而RELS算法由于需要考虑对噪声进行建模,若噪声模型的阶次选择不当,也会致使参数无法收敛。RRIVLS和RIVLS采用辅助变量的方式,一定程度上抑制了有色噪声干扰对参数辨识的影响,保证了参数的无偏估计性,且RRIVLS算法能够对观测得到的数据进行一次滤波预处理,使得参数的收敛过程相比RIVLS算法更为平滑。
综合来看,各算法的收敛结果均有所差异,因此需要后续试验进行辨识结果的验证比对。各算法在10°/10°Z形试验数据和20°/20°Z形试验数据上的最终参数辨识结果分别如表2和表3所示。
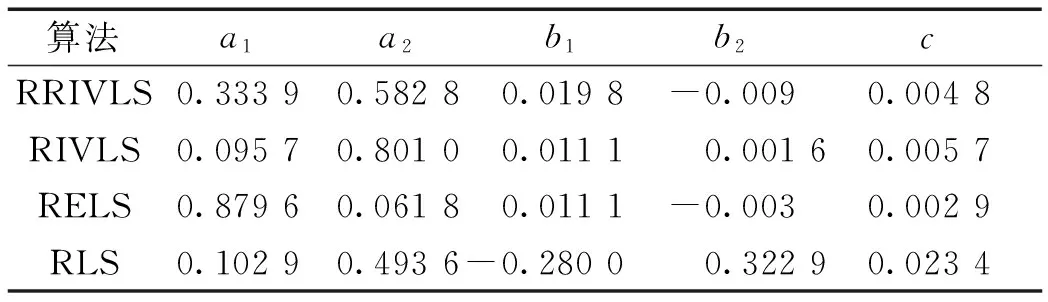
表2 式(7)的参数辨识结果(10°/10°Z形试验)Table 2 Parameter identification results of formula (7) (10°/10° zigzag test)

表3 式(7)的参数辨识结果(20°/20°Z形试验)Table 3 Parameter identification results of formula (7) (20°/20° zigzag test)
对表2和表3的参数辨识结果根据式(6)计算,对应的K、T1、T2、T3和δr的计算结果如表4和表5所示。

表4 式(1)的参数计算结果(10°/10°Z形试验)Table 4 Calculation results of parameters in formula (1) (10°/10° zigzag test)

表5 式(1)的参数计算结果(20°/20°Z形试验)Table 5 Calculation results of parameters in formula (1) (20°/20° zigzag test)
考虑到系统辨识方法在辨识参数较多时,可能存在“参数相消”效应,即所辨识的参数虽然偏离各自的真值,但同样可以使误差函数极小化,从而使得模型的输入输出特性与试验数据拟合得很好。因此为了验证表4和表5的参数辨识结果的准确性,这里选取野本标准法[18]计算的K、T参数为标准进行比对,野本标准法是一种通过Z形试验数据曲线在图解分析的基础上,直接求取船舶操纵响应模型K、T参数的计算方法,尽管该方法计算的参数精度也存在一定的误差,但在一定程度上也能为表4和表5的参数辨识结果提供一定的参数真值理论参考标准。为了将表4和表5的辨识结果与野本标准法进行K、T参数的比对,同时考虑到船舶在进行低频运动时,可将式(1)的二阶线性响应模型近似降阶为一阶线性响应模型[19]:
式中T=T1+T2-T3。
对表4和表5的参数结果按照上述进行换算,其换算结果和野本标准法的计算结果分别如表6和表7所示。
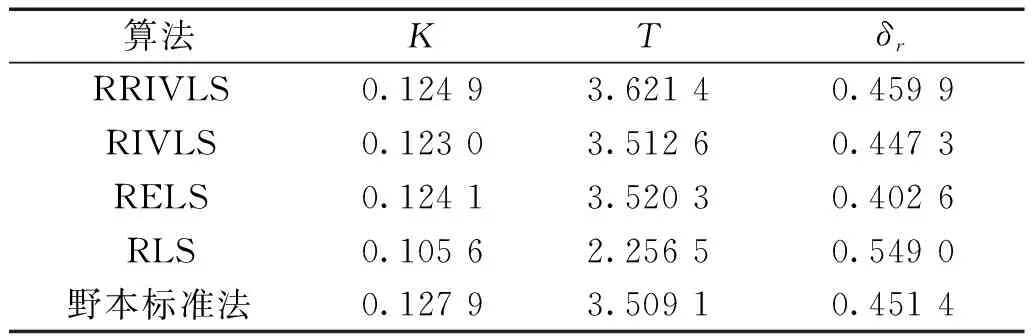
表6 K、T值的计算结果表(10°/10°Z形试验)Table 6 Calculation result table of K and T values (10°/10° zigzag test)

表7 K、T值的计算结果表(20°/20°Z形试验)Table 7 Calculation result table of K and T values (20°/20° zigzag test)
由表6和表7的计算结果可知,野本标准法分别在10°/10°Z形试验和20°/20°Z形试验所计算的K、T和δr参数值具有一定的误差,这是因为计算所采用的Z形试验数据是在真实海洋环境条件下采集的,而海洋环境的实时变化都会对船舶操纵性参数产生一定的影响。因此,野本标准法通过不同的Z形试验数据所计算得到的K、T和δr参数值具有一定的误差是正常的。同时注意到表6和表7中RRIVLS、RIVLS和RELS所辨识参数换算的K、T值与野本标准法计算的K、T值都较为接近,只有RLS算法所辨识参数换算的K、T值与野本标准法的误差较为显著;而对于参数δr,RRIVLS、RIVLS和RELS辨识的参数δr值与野本标准法计算的δr值也都较为接近,而RLS算法所辨识的δr值与野本标准法计算的δr值在10°/10°Z形试验中的误差较为显著。综合来看,RRIVLS、RIVLS和RELS在不同试验中辨识的参数换算结果K、T和δr参数值具有一定的合理性,但并不能证明T1、T2和T3的合理性。因此需要在后续开展模型验证试验,从而以试验的角度证明T1、T2和T3的辨识准确性。
3.2 模型验证
为了进一步对比表4和表5中各算法辨识参数结果的精度,从拟合和泛化2个角度出发对辨识模型的输出特性进行验证:
1)分别将表4和表5中各参数辨识结果代入式(1)中,再分别以10°/10°Z形试验和20°/20°Z形试验舵角数据为输入,对式(1)的微分方程采用四阶龙格库塔法进行求解,从而可得到对应的模型输出曲线。该角度可评价解算得到的航向角与实际测量航向角的拟合精度。各Z形拟合试验的航向角比对曲线和拟合误差曲线分别如图6和图7所示。

图6 10°/10°Z形拟合试验的航向角比对曲线和拟合误差曲线Fig.6 Heading angle comparison curve and fitting error curve of 10°/10° zigzag fitting test
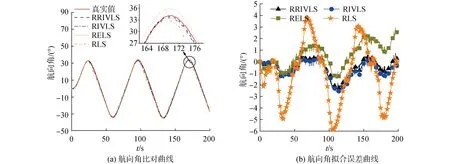
图7 20°/20°Z形拟合试验的航向角比对曲线和拟合误差曲线Fig.7 Heading angle comparison curve and fitting error curve of 20°/20° zigzag fitting test
2)利用10°/10°Z形试验得到的参数辨识结果即表4的参数辨识结果代入式(1)中,对其进行100 s的20°/20°Z形仿真试验,仿真过程利用四阶龙格库塔法进行求解,从而可得到对应的20°/20°Z形航向角泛化曲线。该角度可评价表4中各算法辨识模型的泛化精度。20°/20°Z形泛化试验的航向角比对曲线和泛化误差曲线如图8所示。

图8 20°/20°Z形泛化试验的航向角比对曲线和泛化误差曲线Fig.8 Heading angle comparison curve and generalization error curve of 20°/20° zigzag generalization test
上述所提及误差计算为:

由图6和图7可知,RRIVLS、RIVLS和RELS所辨识的模型相比RLS辨识的模型拥有更高的拟合精度,这一点可以从Z形试验的航向角比对曲线和航向角拟合误差曲线直观看出。而由图8的航向角泛化误差曲线可以得出,各辨识模型的误差曲线随着时间推移在不断的增大,这是因为所比对的20°/20°Z形试验数据是在实际海洋环境中采集的,其中的操纵性参数必然会受到海洋环境的影响而产生变化,因此利用表4的参数进行仿真试验所产生的误差放大现象是正常的。同时,注意到在仿真曲线的前60 s,利用表4中RRIVLS、RIVLS和RELS算法辨识的参数结果所模拟的试验数据曲线仍然能够反映出实际中20°/20°Z形试验的航向角变化特性,且RRIVLS相比其余3种辨识模型的泛化精度更高。这也侧面说明了RRIVLS算法辨识得到参数的准确性和合理性。而RLS算法受到有色噪声的影响,导致辨识的参数偏离真值,因此在图6~8中的误差表现显著。
为了更具体地评价辨识模型的拟合精度和泛化精度,对图6~8中的航向角误差曲线利用均方根误差(root mean squared error, RMSE)和最大绝对误差(maximum absolute error, MAE)进行评价:
MAE=max{|ei|}i=1,2,…,N
式中N为样本数。各Z形试验的RMSE值和MAE值分别如表8~10所示。
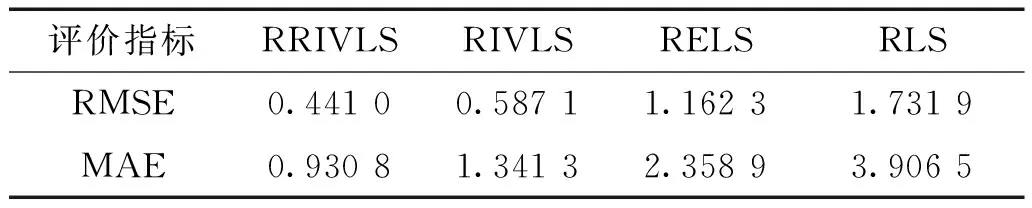
表8 10°/10°Z形拟合试验的RMSE值和MAE值评价表Table 8 RMSE value and MAE value evaluation table of 10°/10° zigzag fitting test
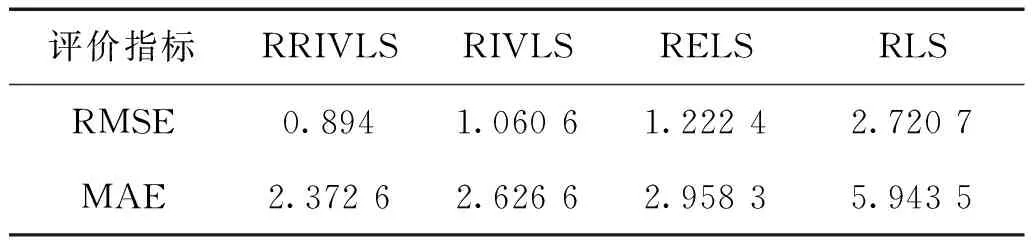
表9 20°/20°Z形拟合试验的RMSE值和MAE值评价表Table 9 RMSE value and MAE value evaluation table of 20°/20° zigzag fitting test

表10 20°/20°Z形泛化试验的RMSE值和MAE值评价表Table 10 RMSE value and MAE value evaluation table of 20°/20° zigzag generalization test
表8~10反映了图6、图7和图8中各辨识模型输出数据与实际航向角数据在不同误差指标下的评价结果。评价结果表明,RRIVLS算法所辨识得到的模型在拟合角度和泛化角度的RMSE指标和MAE指标相比其余算法更小,符合图6、图7和图8中的局部展示结果。且RRIVLS算法相比RIVLS算法,在RMSE指标和MAE指标上均有提升,从而验证了针对RIVLS算法改进的有效性。
3.3 算法实时性分析
本文辨识船舶操纵响应模型的过程中,使用了实船10°/10°Z形试验和20°/20°Z形试验各1 000组数据进行辨识试验,在Windows10系统下的Octave平台中记录了RRIVLS、RIVLS、RELS和 RLS 算法的计算耗时,具体如表11所示。
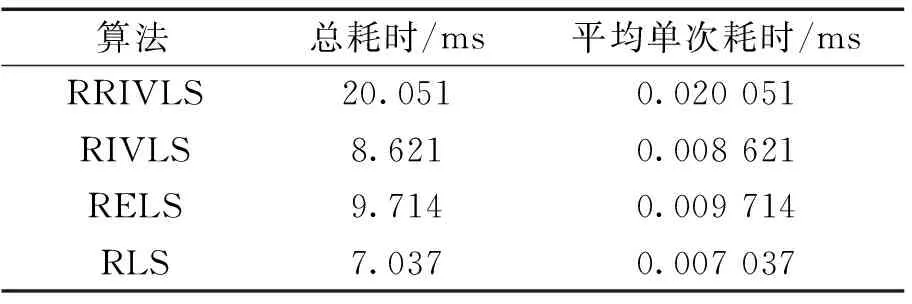
表11 各算法的计算耗时Table 11 The running time of each algorithm
从算法耗时统计结果可知,RRIVLS算法的平均单次耗时为0.02 ms,耗时为另外3种算法的2~3倍。这是由于RRIVLS算法额外考虑了对观测数据的动态滤波,在辨识过程需要额外辨识滤波器的参数,导致了每次辨识循环需要进行2次参数辨识和一次数据滤波,这个过程会额外增加算法的计算耗时,牺牲了RRIVLS算法的实时性,用以提升算法的参数辨识精度,综合来看RRIVLS算法的实时性在可接受范围以内。
4 结论
1)递推修正辅助变量最小二乘法所辨识的模型相比其余三者的辨识模型与船舶实际航向的拟合误差和泛化误差更小,其对应的均方根拟合误差和均方根泛化误差分别可达到1°和2°以下,最大绝对误差分别在3°和4°以下。这说明了修正的递推辅助变量最小二乘法在实船航向过程中能够有效抑制有色噪声的影响,提升了模型辨识的精度,从而为实现精确稳定的航向自适应控制或构建航向在线预报模型提供了基础。
2) 本文的辨识工作仅考虑了二阶线性船舶操纵响应模型,对于船舶的线性运动和中小幅运动比较适应,若船舶处于大舵角或强非线性运动过程中,利用该模型所描述的动态响应过程与实际过程可能会出现较大的偏差。因此,未来可以针对二阶非线性船舶操纵响应模型展开辨识研究。
