循环荷载下TDA掺量对一级道砟动力性能的影响

2023-02-15常建梅李晓慧魏亚辉张伏光冯怀平

中国铁道科学 2023年1期

常建梅，李翔，李晓慧，魏亚辉，张伏光，冯怀平

（1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043；2.石家庄铁道大学土木工程学院，河北石家庄 050043；3.中铁三局集团勘测设计分公司，山西太原 030013；4.中国国家铁路集团有限公司工程管理中心，北京 100844）

与无砟轨道相比，有砟轨道结构具有建设成本低、维修简单等显著优势，是目前使用最多的铁路轨道形式。道床作为有砟轨道结构的重要组成部分，通常由形状各异、棱角分明、表面粗糙的碎石颗粒组成。然而，在列车荷载反复作用下，道砟颗粒不可避免地出现磨耗、破碎、粉化等现象。道砟颗粒几何形态的不断破坏使得道床结构性能日益下降，需要大量繁重的日常养护、维修工作。

为降低和减缓道砟破坏，延长道床的维修养护周期，可对道床结构和材料进行改良。现有改良方法主要有加筋法（土工格栅和无纺布等）、胶结法（道砟胶、聚氨酯和沥青等）和胶垫法（轨下胶垫、轨枕下胶垫和道砟下胶垫）等。土工格栅对于控制道床累积沉降具有显著的效果［1］，但是土工格栅的布设影响道床日常机械养护维修工作。胶结法可约束道砟颗粒间的自由移动，能够有效降低轨道沉降［2］，但实践表明其对道床的排水功能有影响。胶垫法［3］初期改良效果明显，长期使用后材料容易发生老化，失去弹性。因此，发展新型道床改良措施仍然是工程实践的迫切需求，具有重要研究价值。

近年来，废旧轮胎数量日益加剧，对生态环境造成巨大压力，将废旧轮胎橡胶颗粒（Tire-De⁃rived Aggregate，TDA）引入交通基础设施建设的思路受到广泛关注。目前，道砟中添加TDA 的改良方法已逐渐成为研究热点之一［4-10］，该方法具有提高能源利用率、降低道砟磨耗、不影响排水和便于施工等诸多优点，是一种非常具有发展潜力的新型改良措施。Sol-Sánchez 等［4］通过循环加载试验，研究TDA 掺量对道砟集料的沉降和刚度等的影响。Fathali 等［8］在道砟中掺加级配相同的TDA，试验分析了混合集料的各项力学性能。Es⁃maeili等［9］在含沙颗粒的道砟集料中添加不同质量比的TDA，分析了试样的沉降、道砟破碎率及阻尼比等。Signes等［10］通过一系列室内及现场试验，探讨了不同大小及比例TDA 掺入条件下道砟集料的物理力学行为。现有研究主要采用宏观力学试验方法，对颗粒细观层面的力学行为研究尚不充分。

近年来，颗粒几何形状对集料力学性能的影响越来越受到研究者的关注。随着三维激光扫描技术的发展，已有许多学者开始采用该技术研究道砟颗粒几何形状［11-13］。Joseph 等［11］通过三维激光扫描仪获取了颗粒的外形，并提出了针状度、片状度和球度参数的构造算法。井国庆等［12］分析道砟颗粒的三维图形，研究了磨耗试验中道砟的磨耗深度、表面积及体积的变化。Qian 等［13］利用数字图像技术量化了磨耗试验中道砟颗粒的形状、棱角和表面纹理特征，分析了道砟的劣化特征。可见，三维激光扫描技术已为道砟颗粒几何形状的微观分析研究提供了有力手段。然而，在目前TDA 改良道砟的相关研究成果中，有关道砟几何形状微观特征变化的研究尚不充分。

本文针对TDA 一级道砟混合集料，采用动三轴试验和激光扫描方法，研究循环荷载作用下TDA 掺量对道砟动力性能的影响及道砟颗粒形态变化规律。

1 试验材料及方法

1.1 试验材料

道砟采购自国铁集团公布的《铁路用道砟合格生产单位名录》中厂家。道砟材质为硅砂岩，密度为2 650 kg·m-3。按照TB/T 2140—2008《铁路碎石道砟》中新建铁路用一级道砟级配准备，级配曲线如图1所示。

图1 道砟级配曲线

废旧轮胎材料购自唐山某废旧轮胎回收厂家。参考已有研究结论［7］，考虑TDA 尺寸超过8 mm时不会发生渗漏，同时考虑道砟级配范围的下限值为16 mm，因此本文采用8～16 mm 边长的立方体TDA。去除废旧轮胎钢丝，利用闸刀进行切割，形成的TDA 如图2 所示。委托测试机构检测得到的材料参数见表1。

图2 8～16 mm的TDA

表1 TDA材料参数

采用TDA 体积比RC定量描述TDA 的掺量，RC定义为试样中TDA 体积与试样固体颗粒总体积的比值，计算公式如下

式中：VT和VB分别为试样中TDA 体积和道砟体积。

配置混合料时，首先给定RC取值，假设试样的固体颗粒总体积不变，根据式（1）和材料密度计算求得TDA 和道砟质量，然后称取材料搅拌均匀。RC为10%的混合料如图3所示。

图3 RC为10%的混合料

1.2 试验方法

1.2.1 动三轴试验

采用GCTS STX-600大型动三轴仪进行试验，其轴向力最大可加载至1 000 kN，最大加载频率10 Hz。试样直径300 mm，高600 mm。采用相等击实功方法制备试样，混合料分4 层装入压实，每层用25 kg 击实锤人工夯实150 次。为研究TDA 掺量影响，分别制备RC为0%，5%，10%，15%和20%的混合料试样［4，7-9］，加载前试样初始参数见表2。其中，RC为0%试样的密度为1 600 kg·m-3，符合TB 10413—2018《铁路轨道工程施工质量验收标准》的要求。

表2 试样初始参数

试验采用正弦波荷载，由于我国重载铁路运行速度一般在80～100 km·h-1，因此设置加载频率为2.5 Hz。现场测试发现，有砟轨道道床围压在30～60 kPa 范围［14］，因此采用50 kPa 围压。参考文献［15］，最大偏应力qmax分别取250 和300 kPa，最小偏应力qmin取50 kPa。研究［7，16］发现，循环加载10 万次后试样基本处于稳定状态，因此本试验中加载次数为10万次。

1.2.2 激光扫描

采用GD-3dScan 三维激光扫描仪对试验前后道砟颗粒进行激光扫描。真实道砟颗粒及扫描获得的三维道砟颗粒图形如图4所示，激光扫描生成的三维图形可客观、准确反映道砟颗粒的几何形状及表面形态。

图4 道砟颗粒及三维扫描图形

采用Geomagic Studio 软件进行三维图形处理，获得道砟颗粒各种基本几何信息，并通过几何形态评价指标对道砟颗粒几何形状特征开展量化分析。考虑到25.0～35.5 和35.5～45.0 mm 粒径范围内的道砟颗粒数量最多，为便于统计分析，在此范围内随机选取块状、针状及片状道砟进行扫描、分析评价。试验前，清洗和晾晒选出的道砟，并对道砟进行编号、扫描。试验结束后，对于编号的道砟颗粒去除灰尘后重新扫描，然后开展量化评价和分析。

2 三轴试验结果及分析

2.1 应力--应变曲线

图5 为qmax=250 kPa 时不同RC试样的应力-应变曲线。为便于观察对比，图中给出了循环次数分别为1，10，20，40，60，80，100，200，400，600，800，1 000，2 000，4 000，6 000，8 000，10 000，20 000，40 000，50 000，60 000，80 000和100 000 时的曲线。RC=20%试样的轴向应变增加过快，在未到达10 万次循环时就已达终止应变，可见掺量过大时可能发生塑性破坏，不宜采用，因此此处未列出其应力-应变曲线。

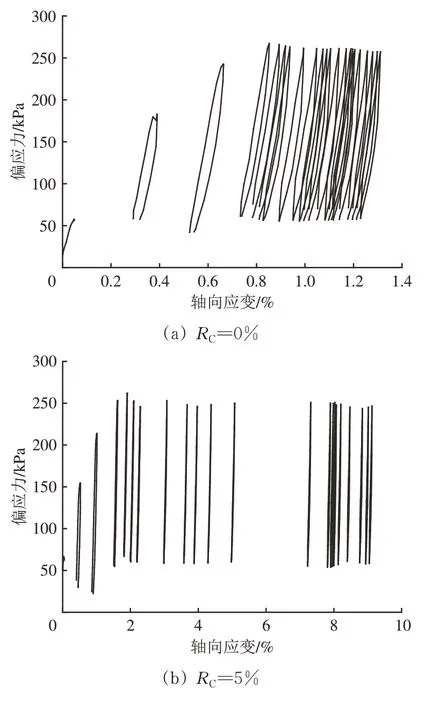
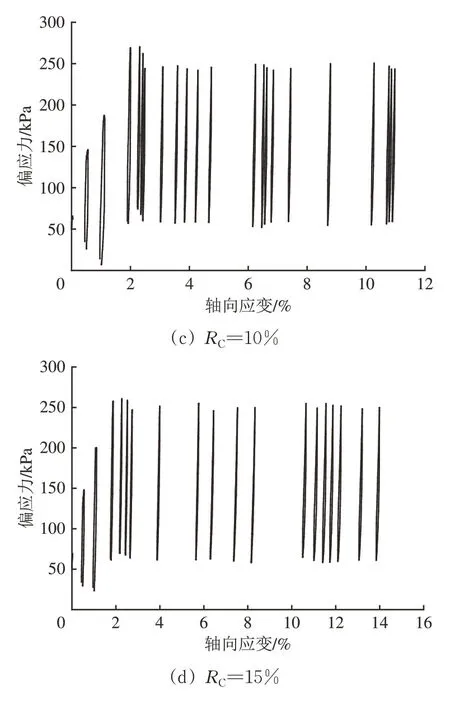
图5 不同RC试样应力-应变曲线

由图5可知：循环约40次后，试样的偏应力才达到目标值；在加载初期，试样的轴向应变增长较快；TDA掺量越大，初期轴向应变增长速度越大。试样采用统一击实功方法制备，TDA 含量高的道砟混合集料不容易压实，初始压实度偏低造成初始应变较大。

图6 为不同RC试样轴向应变与循环次数的关系曲线。由图6 可知：约1 000 次循环后，RC为5%，10%及15%试样的轴向应变增长速度逐渐降低，并趋于稳定，试样基本处于塑性安定状态［17］；TDA 掺量越大，试样最终轴向应变越大。qmax=300 kPa时的试验结果与其相似，不再列出。

图6 不同RC试样轴向应变-循环次数关系曲线

2.2 动弹性模量

动弹性模量是表征材料动弹性变形阶段应力-应变关系的一个重要力学指标。动弹性模量Ed计算公式为

式中：εmax和εmin为最大偏应力qmax和最小偏应力qmin对应的应变值。

不同RC试样动弹性模量与循环次数的关系曲线如图7 所示。由图7 可知：随着循环次数不断增加，集料的动弹性模量出现不同程度的波动，这符合粗颗粒集料特征；qmax=250 kPa时，随循环次数增加，5%试样的动弹性模量呈增加趋势，10%试样动弹性模量略有降低，15%试样的动弹性模量先降低然后基本保持在130 MPa；qmax=300 kPa时，5%及10%试样动弹性模量随循环次数增加主要发生上下波动，15%试样的动弹性模量随循环次数增加先缓慢降低，然后基本保持稳定。

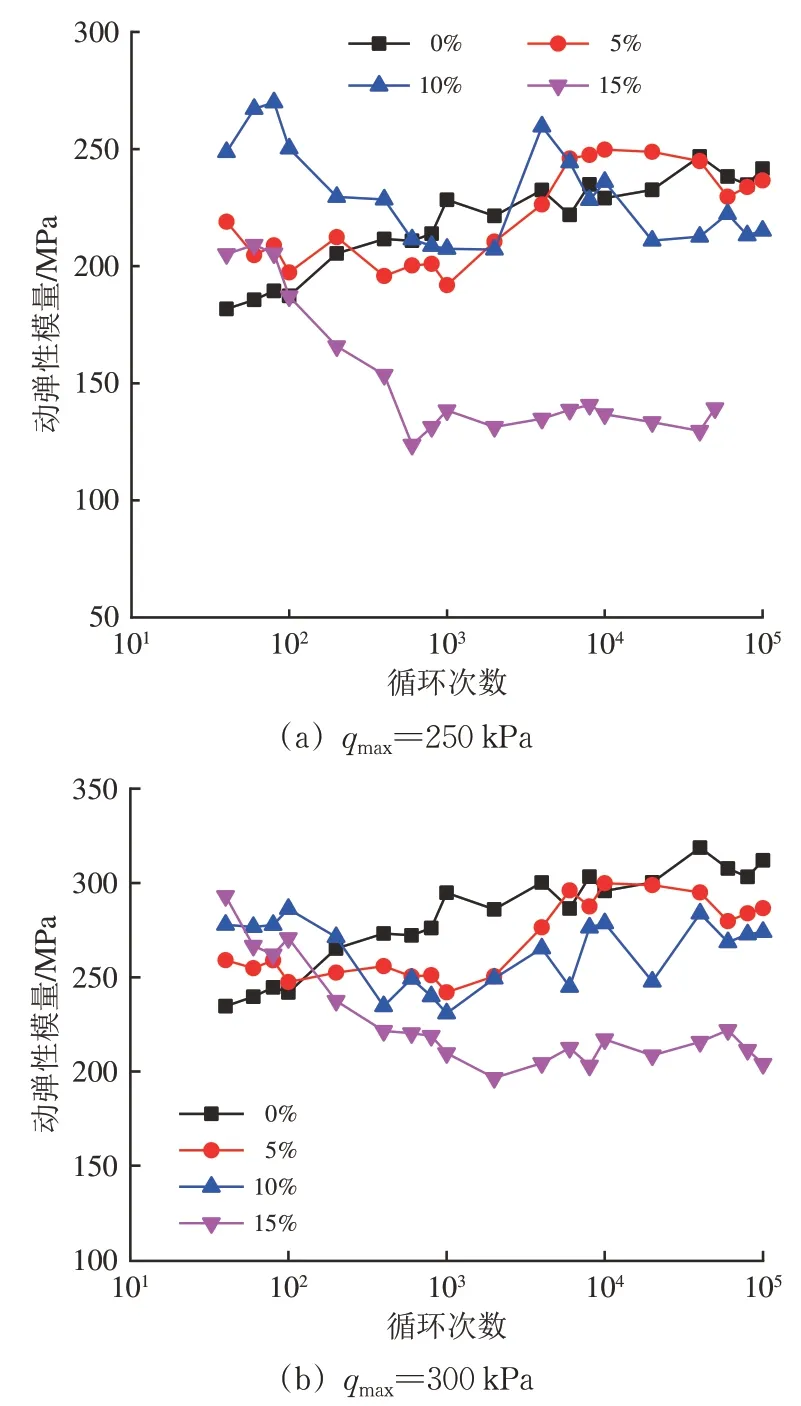
图7 动弹性模量与循环次数关系曲线

图8 为试样动弹性模量与RC的关系曲线。由图8 可知：试样的动弹性模量随RC的增加而降低，且当RC超过10%时动弹性模量下降幅度增大。TDA 刚度显著低于道砟，两者泊松比等其他力学参数相差也较大。混合集料中道砟颗粒相互接触形成主要的承载骨架，TDA 分布在承载骨架的空隙中起到缓冲传递作用。当TDA 掺量较小时，对集料的承载能力影响不大。但当TDA 掺量较大时，将影响承载骨架的形成，对结构刚度的影响较大。

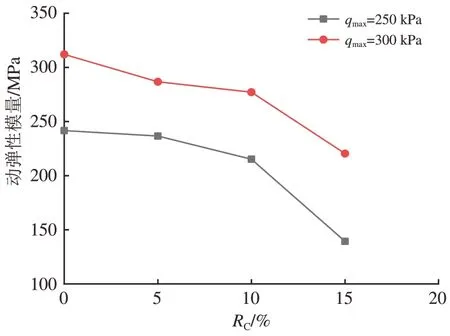
图8 动弹性模量与RC关系曲线

2.3 阻尼比及破碎指数

阻尼比是材料动力性能的重要指标之一。由于试样滞回曲线上下左右均不对称，因此参考肖建清等［18］方法计算阻尼比。在加载初期，试样处于逐渐密实阶段，道砟与TDA 相对位移较大，因此阻尼比出现剧烈降低现象。约100 次循环之后，阻尼比基本保持稳定。

图9 为试样阻尼比与RC的关系曲线。由图9可知：试样阻尼比随RC增加而增大，表明集料耗能能力不断提高；qmax越大，阻尼比随RC增加而增大的速度越大。

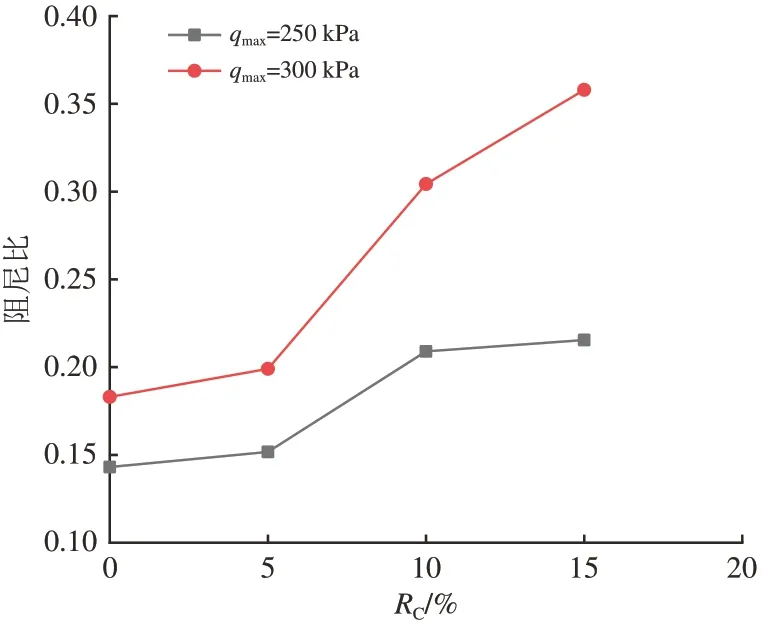
图9 阻尼比与RC关系曲线

道砟颗粒破碎是荷载作用下损耗能量的形式之一。本文采用Indraratna 等［19］提出的破碎指标衡量道砟破碎程度，各试样破碎指数与RC的关系曲线如图10所示。由图10可知：随着RC的增加，破碎指数持续降低，表明TDA 可以有效降低道砟的整体破碎程度。

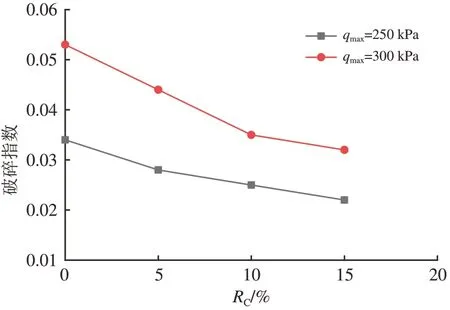
图10 破碎指数与RC关系曲线

2.4 TDA合理掺量

TDA 的添加对道砟集料力学性能产生复杂影响。试验结果表明，随TDA 掺量的增加，混合集料变形增加、动弹性模量降低、阻尼比增加、道砟破碎率降低。因此，需综合考虑以上影响来确定合理的TDA掺量。

首先，TDA 掺量不宜过大，当RC为20%时，试样发生塑性破坏。其次，对于道床弹性模量，一般国家的行业规范中有明确规定，例如日本和法国要求新建道床弹性模量不小于100 MPa，德国要求达到120 MPa 以上，美国则要求位于207～276 MPa 之间。此外，阻尼比反映材料的耗能能力，适当的阻尼比能够减小荷载的冲击、共振等作用，但阻尼比过大却有可能在卸载时引发不稳定变形，造成危险。因此，综合考虑弹性模量和阻尼比的影响作用是确定TDA合理掺量的基本要求。

参照Esmaeili 等［20］的方法，分别对动弹性模量和阻尼比进行最大最小归一化处理。试样动弹性模量和阻尼比归一化值与RC的关系曲线如图11 所示。由图11可知：2个应力水平下动弹性模量和阻尼比归一化值的曲线相交点对应RC均位于10%～15%之间。考虑体积比为15%时试样的塑性变形较大，在充分发挥TDA 降低道砟破碎作用的同时，RC可选取在10%以内，并且此时集料弹性模量也满足主要发达国家行业规范要求。

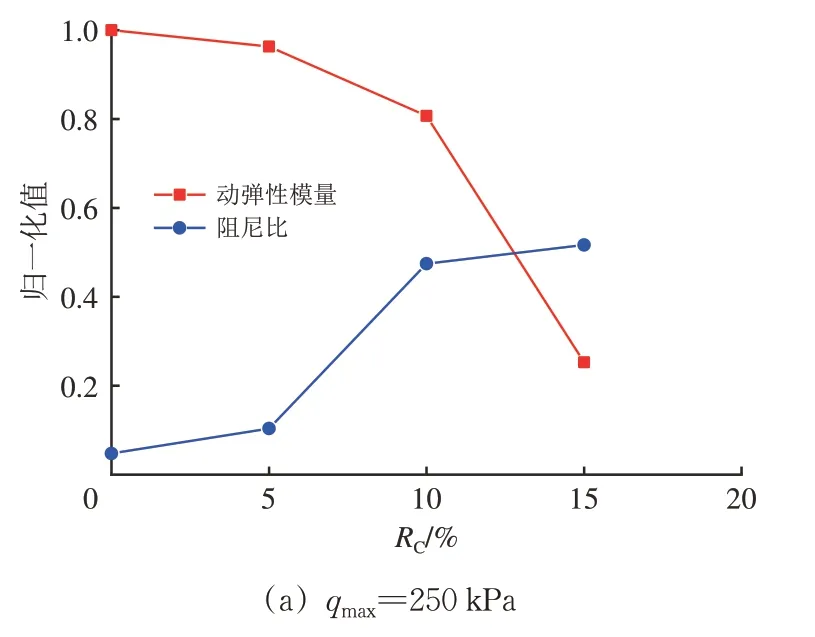
图11 动弹性模量和阻尼比归一化值与RC关系曲线

3 道砟颗粒几何形态

道砟颗粒的不规则几何形状对道床物理力学性能有重要影响。研究表明，三维数字图形可高精度客观反映颗粒表面的空间信息［21］。因此利用试验前后道砟颗粒的三维图形，对qmax=250 kPa 时RC为0%及10%的试样开展颗粒几何形态对比分析。

3.1 基本破损状态

图12 为随机选中的不同粒径范围内典型形状道砟，包括块状、针片状。不同形状道砟颗粒数量见表3。

图12 典型形状道砟

表3 不同形状道砟颗粒数量

试验后的统计结果表明，0%试样中道砟破损共9 块，10%试样中道砟破损共7 块，分别占总颗粒数的14%和11%。与洛杉矶试验［21］相比，道砟颗粒破坏比例较低。0%及10%试样中的道砟破损形式基本相同，主要是在尖角、棱边、表面处发生局部破坏和磨损等，未发现整体劈裂。

图13 为某一破损道砟试验前后扫描所得的三维图形及磨耗深度云图，可确定道砟发生破损的位置及磨耗深度。由图13 可知：该道砟在上端尖角及右侧棱边处发生了破损；根据磨耗深度云图，最大磨耗深度约为2.9 mm。统计所有破损道砟颗粒，发现0%和10%试样中道砟颗粒的最大磨耗深度分别为2.5～8.4 和2.9～4.1 mm，可见RC为10%试样中TDA有效降低了道砟最大磨耗深度。

图13 试验前后三维图形及磨耗深度云图

采用Geomagic Studio 软件可获得道砟颗粒的体积及表面积。统计发现，试验前后单个道砟颗粒的体积及表面积均发生减少。0%试样中道砟颗粒的单个体积和表面积损失率分别位于1.24%～4.92%及1.67%～6.95%，10%试样单个道砟颗粒的体积和表面积损失率位于1.17%～2.99%及1.61%～4.31%。可见，添加TDA 同时降低了单个道砟的最大体积损失和面积损失。统计劣化道砟颗粒的平均体积损失率及面积损失率，发现0%试样中劣化道砟的平均体积损失率为2.72%、平均面积损失率为3.71%；10%试样的中劣化道砟为1.69%及2.38%，可见10%试样颗粒的平均体积和面积损失率均有所降低。

3.2 整体几何特征

Pen 等［22］指出可以从整体、局部（棱角和纹理）2 个层次对颗粒几何形状特征进行量化评价，评价指标相互独立。

采用形状系数φ［23］评价道砟颗粒整体形状特征，其计算公式如下

式中：S0为颗粒表面积；S为对应等体积球体的表面积。

形状系数φ越大，代表颗粒的形状越趋近球体。试验前后0%试样道砟颗粒的平均形状系数分别为0.68 和0.69，10%试样中道砟颗粒的平均形状系数分别为0.70 和0.71。可见，0%及10%试样中道砟颗粒主要发生尖角、棱边的破损，颗粒的形状系数略有上升，但整体形状特征变化较小。

3.3 局部几何特征

基于二维图形的颗粒局部几何特征分析思路是分类评价，其评价指标比较全面，例如表征棱角突出程度的指标有棱角指数、凸度和尖角度等，评价表面粗糙程度的指标有表面分形维数、表面质地系数和等效椭圆周长比等。

然而在三维条件下，各种空间几何元素的关联性变得更强，直接扩展二维图形的分类评价思路，得出的评价结果经常会出现适用性不强、表达边界不清晰等问题。例如，将凸度指标扩展至三维图形下表达时，将不可避免地包含了颗粒表面粗糙的特征；将表面质地系数扩展至三维情况时，不可避免地涵盖了颗粒棱角凸出的特征。

本文采取不分类的综合评价思路，依据棱角、棱边和粗糙表面等局部特征区域都具有曲率较大的特征，提出基于三维图形的局部特征综合系数AS，实现对道砟局部特征的量化评价。计算公式如下

式中：SL为敏感区域面积，指曲率大于设定值的颗粒表面部分面积。

局部特征综合系数AS数值越大，代表局部特征越显著。利用三维图形处理软件Geomagic Stu⁃dio，设定曲率敏感度，可获取颗粒总表面积和敏感区域面积，然后计算AS。图14 为选定曲率敏感度为0.5 时，某一道砟颗粒的敏感区域（红色区域），可见棱角、棱边及主要粗糙表面均被有效识别。

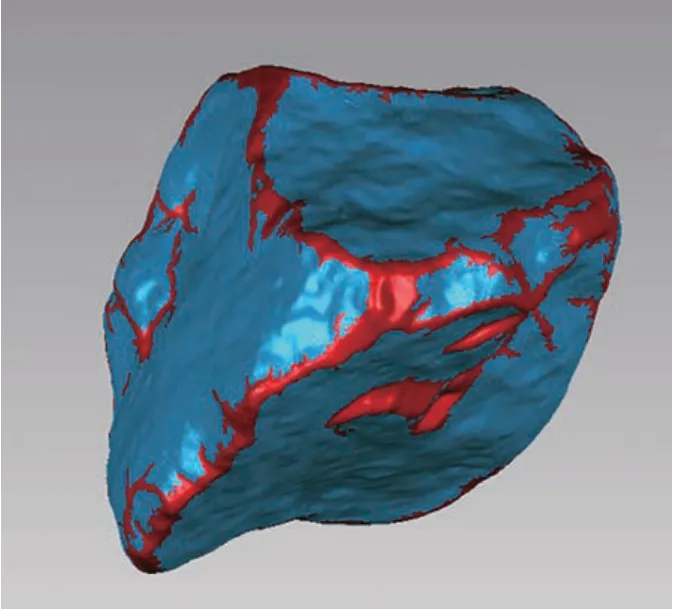
图14 道砟曲率敏感区域

统计结果表明：试验前后0%试样道砟颗粒的AS平均值分别为0.74 和0.62，而10%试样分别为0.62 和0.62。可以看出，0%试样的道砟AS在试样过程中发生明显降低，而10%试样中道砟AS试验前后基本没有变化，即10%TDA 的添加有效降低了道砟颗粒局部破坏程度，与0%试样相比降低程度为16%。

对比试验前后单个道砟颗粒的AS值可知：0%试样中的道砟AS值在试验后均有所减小；而10%试样中大多数道砟AS值在试验后发生减少，但也有部分颗粒的AS值不变或略有升高。分析原因，在循环加载初期，道砟颗粒主要发生尖角折断或棱边破损，折断或破损处会产生更多的局部敏感区域，此时道砟AS值表现为升高。随着循环次数的增加，道砟颗粒间变得更加紧密，道砟颗粒相对发生摩擦、滑移，道砟颗粒的尖角和棱边被不断磨耗，局部特征敏感区域不断减小，道砟颗粒的AS值不断减小。0%试样在后一阶段中发生磨耗的程度较大，因此道砟AS值最终均表现出减小。10%试样中由于TDA 的影响，道砟颗粒在这一阶段发生的磨耗较小，因此道砟颗粒的AS值表现出减小、不变及升高等不同现象。可见TDA 在减缓磨耗、保持颗粒局部特征方面可发挥作用。