基于三维Copula函数的滦河流域干支流丰枯遭遇研究
2023-02-14魏琳杨学军王旭东
魏琳,杨学军,王旭东
(海河水利委员会水文局,天津 300170)
滦河是海河流域的重要河流之一,研究滦河水系的丰枯规律,分析滦河流域主要产流区干支流丰枯遭遇问题,对该地区防洪抗旱、雨洪资源利用、水资源的合理开发提供科学的技术支撑。因此,本文对滦河干流、潵河支流、青龙河支流3条主要干支流的丰枯遭遇问题开展分析研究,基于1956—2016年近61 a径流量长系列水文资料,选取干流重要控制断面潘家口、潵河支流潘大区间、青龙河支流桃林口为主要控制站(区间),采用Copula函数构建具有相依关系的三维联合分布模型,研究不同干支流、不同量级来水量的遭遇概率及条件概率分布,实现准确定量丰枯遭遇的分析,为滦河流域洪水资源利用及调度决策提供技术参考。
目前,传统丰枯遭遇研究方法主要是通过实测资料建立变量之间的相关关系,或者通过典型年法分析各流域来水量之间的遭遇关系[1],难以量化不同条件下的丰枯遭遇;现有的水文多变量概率分析方法主要有多元正态分布法、特定边缘分布构成的联合概率分布法、非参数法、将多维分布转换成一维方法、经验频率法等,但这些方法不能准确描述变量内部的相依关系。多维Copula函数的构建既能反映单个随机变量分布特征,又能呈现变量之间的相依性,是一种可连接多个变量边缘分布的联合分布函数,可反映水文事件随机性、相依性的特点,是解决多变量联合分布问题的值得尝试的工具。因此,采用Copula函数对滦河流域干支流丰枯遭遇问题进行分析,为滦河流域滦县以上水资源合理利用提供指导。
1 基于Copula方法的丰枯遭遇风险分析
1.1 Copula函数及方法
Copula理论是在1959年由Sklar提出的,可以将任意一个m维联合累积分布函数分解为m个边缘分布和一个Copula函数。变量的分布特性采用边缘分布函数,变量之间的相关性采用Copula函数进行衔接[2],即在变量的边缘分布函数已知的前提下存在一个Copula连接函数,形成多元联合分布。
Copula为[0,1]之间的联合概率分布函数。假设F为一个m维分布函数,其边缘分布为F1,F2…Fm,那么存在一个m维Copula函数C,使得对任意X∈Rm有:

若F1,F2…Fm是连续的,则该函数C是惟一的,否则C由RanF1×RanF2×…×RanFm惟一确定;相反,若C是一个m维Copula,F1,F2…Fm为一元分布函数,则由式(1)定义的函数F是一个m元分布函数,其边缘分布为F1,F2…Fm。
1.2 常用的Copula函数
Copula函数总体上可以划分为3类,即椭圆型、二次型、Archimedean型。目前,水文上常用的Archimedean Copula函数族应用最为广泛,三维非对称型Copula函数[3]主要有以下3种。
(1)Gumbel Copula函数,表达式为:

(2)Clayton Copula函数,表达式为:

(3)Frank Copula函数,表达式为:
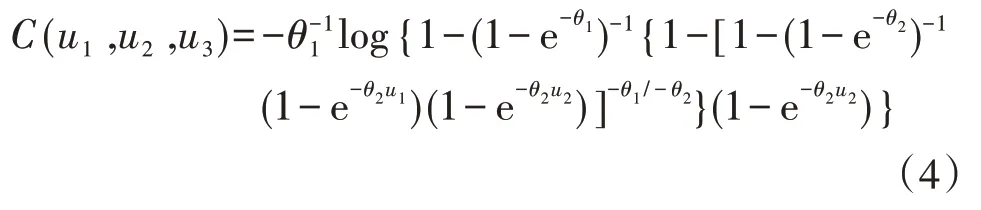
式中:C(u1,u2,u3)为三维的Copula函数;u1,u2,u3分别为边缘分布函数,u1=F1(x1),u2=F2(x2),u3=F3(x3);θ1,θ2分别为Copula函数的参数。
1.3 重现期及遭遇分析
能够对径流量丰枯遭遇的概率及条件概率的准确分析是该方法的明显优势。假定X1,X2和X3分别为具有相依关系的变量序列,事件(x1,x2,x3)的联合概率分布F可表示为[4]:

相应的联合重现期可表示为:

式中:F(x1,x2,x3)为联合概率分布函数,x1,x2,x3分别代表X1,X2,X3的取值;P为不超过概率;T(x1,x2,x3)为联合重现期。
当水文事件相互独立时,联合概率分布函数可表示为:
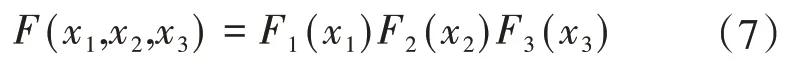
相应的重现期可表示为:

式中:F1(x1),F2(x2),F3(x3)分别为X1、X2和X3的边缘分布函数;T为变量相互独立时的重现期;T(x1),T(x2),T(x3)分别为X1,X2和X3的重现期;其余变量含义同上。
1.4 参数估计和拟合优度检验
Copula函数的参数估计主要有两种类型的方法,一种是非参数法,另一种是参数法。其中,非参数法要求有明确的Kendall的τ与Copula参数θ的表达式,一般二维Copula函数参数估计用得较多,对资料长度也有一定要求;参数法相对比较灵活,本文三维Copula函数的参数确定采用参数法中IFM(Inference of Functions for Margins)方法,该方法主要包括两方面内容:①采用极大似然法估计边际分布中的参数;②采用极大似然法估计Copula函数中的两个参数。
最优函数的选取采用拟合优度检验,先假定不同的Copula函数,采用不同检验方法进行择优。目前,检验方法有多种,包括Kolmogorov-Smirnov检验(K-S检验)、偏差、均方根误差、AIC准则等,本文采用常用的均方根误差进行拟合优度检验。
2 研究区概况
滦河发源于河北省丰宁县巴彦图古尔山麓,始称闪电河,流经内蒙古自治区正兰旗至大河口纳吐力根河后称大滦河,至河北省隆化县郭家屯附近与小滦河汇合后称滦河,郭家屯以下至潘家口河道蜿蜒曲折,穿行于燕山山脉,过桑园峡口进入迁安盆地,至滦县城关流出燕山山脉,于乐亭县兜网铺入渤海。滦河干流与伊逊河汇合处以上为滦河上游,多为坝上草原,地势平缓,支流少;滦河三道河子以下至干流滦县以上为滦河中游,地处燕山腹地,地形起伏较大,山岭重叠,沟谷纵横,区间有6条较大支流汇入,均属山溪性河流,河道比降大,水流速度快。在干流和支流青龙河建有潘家口、大黑汀和桃林口3座大型水库。燕山迎风坡是暴雨多发地带,也是滦河洪水的主要发生区和径流产流区。因此,选取滦河中游潵河、青龙河及滦河干流为研究对象,开展干支流丰枯遭遇分析。
3 滦河干支流丰枯遭遇分析
3.1 选取干支流特性分析
滦河干流选取潘家口水库站来水、潵河选用潘大区间来水、青龙河选取桃林口水库站来水作为代表系列,包括1956—2016年共61 a数据,假定常用水文变量频率分布为P-Ⅲ型分布,采用现状参数估计较为准确的线性矩法进行初步估计并进行适线,各河流特征值及不同概率下的来水量详见表1。

表1 滦河干支流代表站特征值及特征来水量(不超过概率)
由表1可以看出,滦河干流多年平均径流量为15.58亿m3,青龙河为6.86亿m3,潵河为2.78亿m3,其中支流青龙河多年平均径流量大于潵河。丰水年滦河干流径流量为19.72亿m3,青龙河为9.07亿m3,潵河为3.72亿m3;枯水年滦河干流径流量为8.3亿m3,青龙河为2.92亿m3,潵河为1.24亿m3。
3.2 Copula函数的最优选取
3.2.1 边缘分布函数选取
日常工作中,常采用P-Ⅲ型分布作为水文变量的分布线型。由于不同的水文气象特征,各地区来水量系列也可能服从其他分布,因此我们假定P-Ⅲ型分布、对数正态分布、Gumbel分布、极值分布4种常用的分布线型,采用均方根误差、绝对值误差、AIC信息准则、PPCC检验法4种拟合准则进行线型拟合,选出拟合效果最好的分布线型,其中均方根误差(RMSE)、绝对值误差(ABS)及AIC信息准则越小越好,PPCC越接近于1越优,结果详见表2。

表2 边际分布的拟合优度检验
由表2来看,对潵河潘大区间而言,P-Ⅲ分布具有最小的ABS和RMSE值,表明P-Ⅲ分布为该站最优线型;对滦河干流潘家口水库站而言,P-Ⅲ分布具有最小的ABS和RMSE值,表明P-Ⅲ分布为该站最优线型;对青龙河桃林口水库站而言,P-Ⅲ分布具有最小的ABS、RMSE和AIC值,表明P-Ⅲ分布为该站最优线型。经综合考虑,选定P-Ⅲ分布作为研究潘家口、桃林口、潘大区间来水量数据的分布线型。
3.2.2 相关性分析
不同的Copula函数有各自的特性,其中Gumbel Copula函数和Clayton Copula函数适用于具有正相关关系的变量;Frank Copula函数对相关关系为正、负的变量均可;Ali-Mikhail-Haq Copula函数适用于具有弱相关关系的变量。因此,根据变量之间的相关关系,初选适宜的Copula函数。本文采用线性相关系数及秩相关系数,对变量之间的相关性进行分析计算,结果详见表3。

表3 相关性计算结果
由表3可以看出,三站径流量数据之间都属于正相关关系,从Copula函数对变量相关关系的要求来看,Gumbel Copula、Clayton Copula及Frank Copula函数适用于该研究,因此对这3种Copula函数开展拟合优度检验。
3.2.3 Copula函数参数确定及拟合优度检验
为检验Copula函数的拟合精度,需分析比较各个数据点对(xi,yi,zi)的经验累积概率和理论累积概率的一致性[3]。设N为水文系列观测样本对数,按照x升序排列所得数据系列为(x1,y1,z1),(x2,y2,z2)…(xi,yi,zi)…(xN,yN,zN),三维经验联合概率分布采用下式计算:
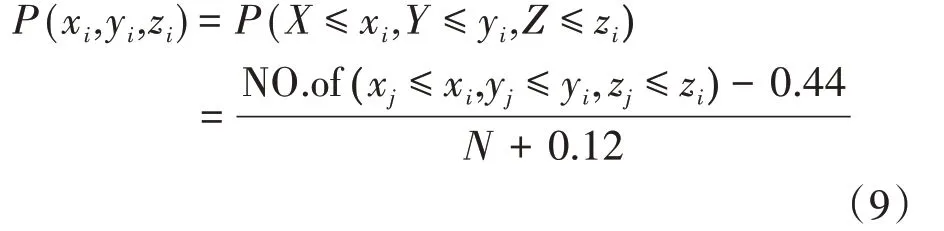
根据极大似然法计算各Copula函数的参数[5],结果详见表4。根据式(9)计算滦河干流、潵河、青龙河的经验联合频率值,通过Copula函数计算三变量的理论联合频率,将所得的经验联合频率与理论联合频率点绘在图1中。由图1可以看出,经验频率点和理论频率点均匀分布在45°线附近,表明三变量的经验频率点和理论频率点拟合较好,说明选择的联合分布函数均是合理的。由于Gumbel、Frank、Clayton Copula函数中采用Frank Copula函数拟合最好,选取Frank Copula为最优函数。
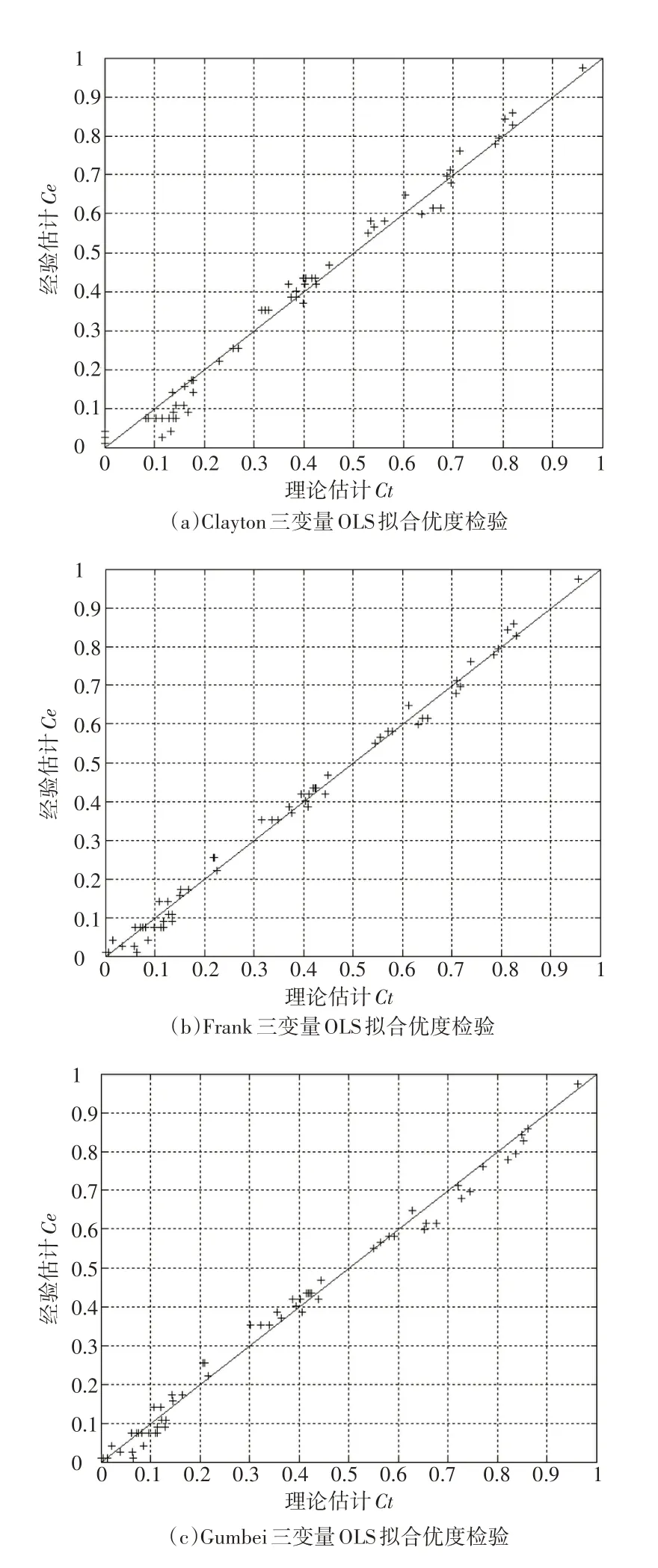
图1 滦河干流、潵河、青龙河年来水量经验频率与不同理论频率的拟合
为确定滦河干流、潵河、青龙河来水量拟合最好的Copula函数,需要进行拟合优度检验,本文采用均方根误差(RMSE)检验方法,结果详见表4。根据结果可以看出,初选的3种Copula函数中,Frank Copula具有最小的RMSE值,表明Frank Copula具有最好的拟合优度,对本文选用的滦河干流、潵河、青龙河年来水量数据而言,Frank Copula即为选定的最优Copula函数。

表4 三维Copula函数拟合优度检验结果
3.3 干支流丰枯遭遇分析
从分析得到的滦河干支流径流量的边缘分布和最优Copula函数,可得到各种联合分布和条件概率分布,从而分析不同情况下干支流丰枯遭遇情况,如滦河干流、潵河支流、青龙河支流的年来水量保证率都能达到75%的概率;或者当滦河干流潘家口来水量不足时,遭遇支流潵河及青龙河桃林口水库丰水的概率;或者当干流潘家口为丰水年,遭遇潵河及青龙河枯水年份的概率。通过三维Copula函数的构建,这种问题将迎刃而解[2]。
(1)当滦河干流、潵河支流、青龙河支流的来水量达到某一概率水平的联合概率分布表示如下:

式中:θ1=8.392 3,θ2=8.398 6,为Frank Copula函数的参数;X,Y,Z依次为桃林口水库站,潘大区间,潘家口水库站来水量数据系列;U1=Fx(x),U2=FY(y),U3=Fz(z)分别为各站的边际分布函数,u1、u2、u3为其取值。
由式(10)可得滦河干流、潵河、青龙河同时出现枯水年的概率为F(x,y,z)=C(25%,25%,25%)=P(X≤2.92,Y≤1.24,Z≤8.3)=0.134 2。
滦河干流丰水年遭遇支流潵河、青龙河同时出现枯水年的概率为F(x,y,z)=C(25%,25%,75%)=P(X≤2.92,Y≤1.24,Z≤19.72)=0.174 4。
因此,滦河干流、潵河、青龙河同时出现枯水年的概率为0.13,滦河干流丰水年遭遇支流潵河、青龙河同时出现枯水年的概率为0.17。也就是说,3条河同时出现枯水的概率不大,滦河干流丰水年两条支流枯水年出现的概率也不大。
(2)假定某一干支流的来水量水平已知,需要据此预测其他干支流的来水量时条件概率出现的情况,本文亦可以准确计算得出。各种水平年遭遇组合的条件概率如下。
已知滦河干流为枯水年时预测支流潵河及青龙河同时发生枯水年的概率为F(y,x|z)=P(Y≤1.24,
已知滦河干流为特丰水年时预测支流潵河及青龙河同时发生枯水年的概率为F(y,x|z)=P(Y≤1.24,=0.184 2,即滦河干流出现枯水年份两条支流同时发生枯水年的概率为50%,滦河干流为特丰水年支流发生枯水年的概率为0.18。
图2和图3为滦河干流潘家口水库分别为枯水年(P=25%)和特丰水年(P=95%)时遭遇潵河、青龙河不同量级水量的概率分布,由此可以简单直观得到相应的条件概率,为滦河流域水资源的决策分析提供技术支撑。
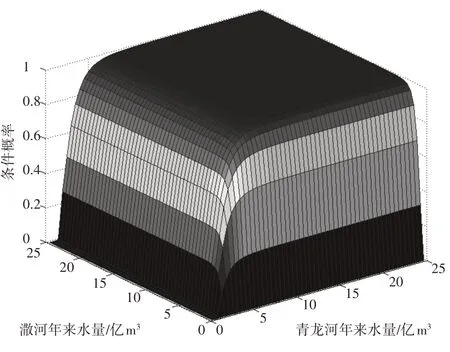
图2 滦河干流枯水年(P=25%)条件下潵河及青龙河条件概率曲线

图3 滦河干流特丰年(P=95%)条件下潵河及青龙河条件概率曲线
4 结论及展望
(1)三维Copula函数通过任意的边缘分布和相关性结构来构造多维联合概率分布,在水文丰枯遭遇的应用上改变了传统方式对该问题难以准确量化的缺陷,该函数方法形式灵活多样,考虑了变量间的相关关系,为研究多维联合概率分布及丰枯遭遇提供了新的有效手段,可在生产实践中应用。
(2)针对滦河干支流丰枯遭遇的分析,采用三维Frank Copula函数拟合最好,从而可以得到不同量级下的干支流丰枯条件下的概率和重现期,为滦河流域洪水资源利用及科学管理提供必要的理论依据参考。
(3)基于Copula函数的三变量联合分布的来水频率分析方法能更好地描述来水特征量之间的关系,且对边缘分布类型没有限制,在现有实际来水频率分析计算中有较大的优越性,但未来仍需对参数估计、函数选择进一步开展研究,使得模型更加完善。
