基于全局特征点匹配的全局定位方法

彭泽鑫，曾 碧，刘建圻

广东工业大学 计算机学院，广州 510006

移动机器人的定位问题是同步定位与建图（simultaneous localization and mapping，SLAM）[1-2]的一个基本问题，指的是移动机器人根据传感器信息去推断当前的位姿。定位问题大致可以分为局部定位与全局定位[3]。局部定位指的是在已知机器人的初始位姿的情况下，通过适应机器人运动噪声和传感器数据来推测机器人下一帧的位姿。全局定位指的是在未知机器人的初始位姿，通过传感器数据和地图数据等进行匹配推测出机器人当前的位姿。全局定位是在缺少初始位姿的情况下推测出当前的位姿，所以它比局部定位更加困难。

全局定位问题根据使用的传感器大致可以分为基于视觉的定位方法和基于雷达数据的定位方法。基于视觉的全局定位方法通过把当前帧所对应的图片与图片数据库中的信息进行匹配，以估计机器人当前的位姿，大致可以分为图片到图片、图片到地图的匹配方法[4]。在经典的视觉方案中，大部分都是通过将当前的图片帧进行某种方式的编码，然后再与数据库的关键帧进行对比，从而实现场景的匹配，例如，Singh等人则采用了Gist描述子的方式对地图进行编码，并用之来实现场景的识别[5]。FAB-MAP[6]、RTAB-MAP[7]和ORB-SLAM3[8]所采用的则是基于词袋模型（bag-of-words，BoW）的来实现场景的匹配。基于图像的全局定位方法只能够在机器人曾经采集过关键帧的位置附近定位成功，而且随着数据量的增大，图像与数据库的匹配将越来越困难，误匹配的概率也将随之提高。Kendall等人首次将卷积神经网络（convolutional neural network，CNN）应用到了视觉定位中，他们通过训练PoseNet的方式实现了通过单张RGB图实现了相机在一个6-DOF的空间的定位[9]。Li等人则通过RGB-D相机，采集了点线特征点，并且将这些点线特征通过深度神经网络的形式完成场景的识别[10]。尽管基于神经网络的方法弥补了传统方法的许多缺点，但在局部特征表现良好的典型情况下，其定位性能仍然不如传统方法。

在基于雷达数据的全局定位方法中，比较有代表性的方法之一是蒙特卡洛自适应算法AMCL[11]，它是一个十分经典的多峰概率估计的实现方式，在粒子足够多的情况下，一般能够收敛到较优的位置，然而，AMCL有明显的缺点，例如粒子收敛速度缓慢，计算量较大。Hess等人提出了Cartographer[12]，使用了基于搜索窗口的方法将当前的雷达帧与地图相匹配来实现全局定位，然而，Cartographer基于搜索窗的方法只有当机器人在当前帧的搜索窗口范围内时才可全局定位成功，虽然Cartographer使用了深度优先算法和分支限界法来加速搜索的过程，但是计算量还是十分大。Wang等人提出了一种利用几何结构信息将点云注册到全局点云的方法实现了全局定位，通过在当前点云帧构建全等三角形，并将之在全局点云中寻找与之全等的三角形完成点云注册[13]，然而该方法仅仅考虑了当前帧的点云局部信息，并且匹配速度较低。Liu等人提出了LPD-Net，通过使用网络来对点云提取出一个全局描述子通过该描述子完成点云注册的任务[14]。Kong等人提出了基于语义构建图网络，再通过图网络匹配的方式完成了点云注册[15]。Xiang等人通过对点云数据使用结合编码和机器学习的方法，提出了FastLCD[16]，实现了闭环检测，得到了相对可靠和精确的结果。采用这些方法虽然在算力足够以及特征足够的情况下能够取得较好的效果，但是依赖于GPU，计算量较大，在计算力较低的平台很难有效的运用。

针对以上几类方法存在的缺点，本文提出了一种基于全局特征点匹配的全局定位方法，其计算量小，效率高。本文的主要创新点如下：（1）提出了实时稳定的轻量级特征点提取算法，有效减少了无用特征点的数量。（2）建立了点与点之间的约束，构建了全局描述子，针对该描述子，提出了朴素匹配算法和随机匹配算法，实现了全局特征点的同步匹配，具有较高的匹配精度和匹配速度。

1 系统框架

本文所提出的基于全局定位方法主要由三部分组成：特征点提取、特征点匹配以及全局定位结果的求解。如图1所示，算法事先获取了全局地图特征点，通过实时获取局部地图特征点，将局部地图特征点与全局地图特征点通过随机匹配算法实时匹配，再使用随机抽样一致算法（random sample consensus，RANSAC）根据特征点的匹配结果求解出全局位姿，完成全局定位。全局地图特征点获取阶段发生在全局地图的构建过程中，即让机器人在运行SLAM算法构建全局地图的过程中，实时运行该算法，当全局地图构建完毕后，再进入运行全局定位算法的阶段，通过运行与构建全局地图时一致的算法，实时获得局部地图以及局部地图特征点。

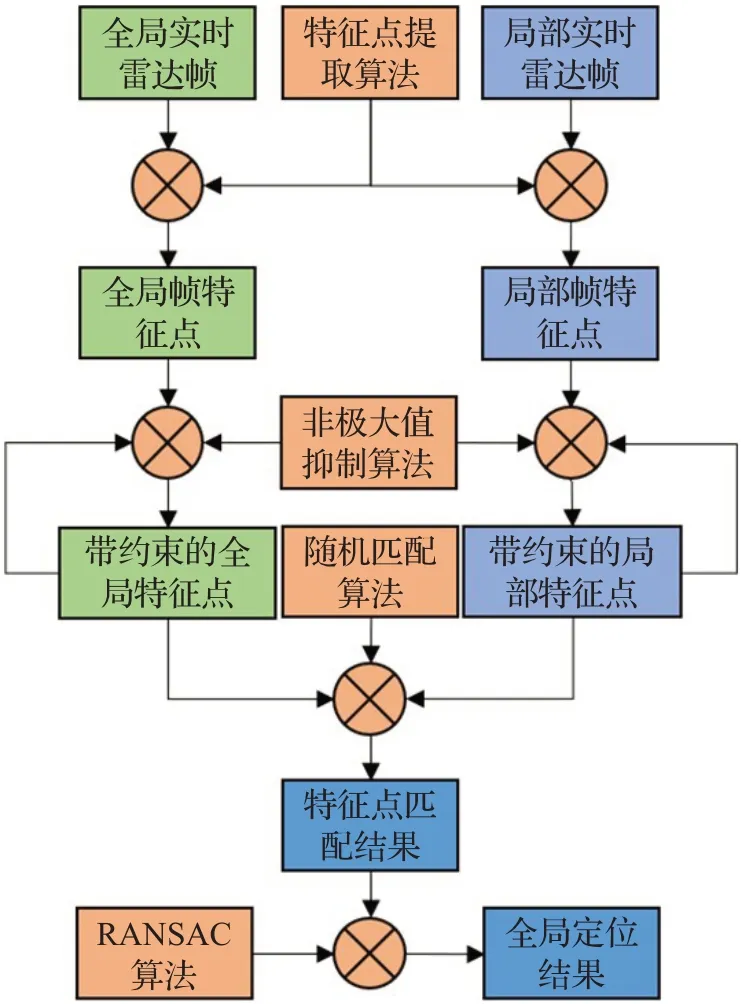
图1 全局定位方法框架Fig.1 System framework of global localization mehod

2 特征点提取

为了后续特征点匹配算法的效率、准确率以及对实时性的要求，本文提出了一种轻量级稳定的特征点实时提取算法。该特征点提取算法具备以下特点：（1）在不同方位扫描的时候都可以提取出该特征点。（2）具有一定的鲁棒性，能够有效地消除噪声影响。（3）所需算力极低。

2.1 特征点的粗提取

如图2（a）所示，算法首先提取当前雷达帧数据H，通过当前机器人的位姿ξ映射到地图坐标系，根据相邻两点间的距离对雷达帧进行切片，同时，为了保证数据的可靠性，舍弃了包含与雷达射线夹角较小的边缘的雷达片段，因为当激光以较小的夹角打到物体平面时，数据不够稳定。再对片段中的每个点进行打分，根据得分阈值得到待筛选的特征点，如图2（b）所示。

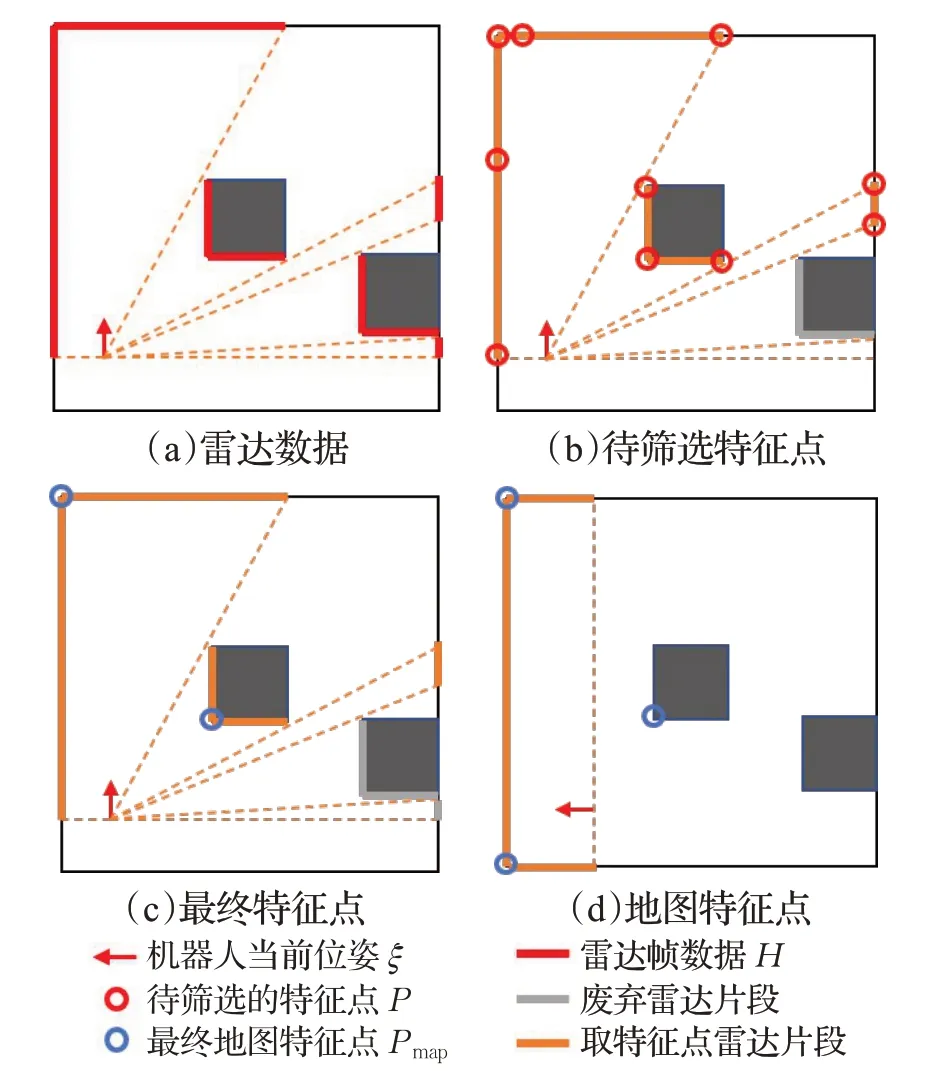
图2 特征点提取算法示意图Fig.2 Schematic diagram of the feature point extraction

这里所采用的得分评估函数是Zhang等人在LOAM[17]中提取特征点时所采用的评估函数。该函数根据当前点的平滑程度进行打分，得分越高的点表示越不光滑。使用该函数可以粗略地提取出角点，后续算法将基于这些提取出来的粗特征点进行筛选，而不是基于原始的雷达数据，大大减小了后续的计算量。将当前雷达帧的点记作H={hk}k=1,2,…,K,hkϵR2，当前雷达帧所切割出来的片段记作Hi,i=1,2,…,N，Hi⊆H，Hi∩Hj=∅,i≠j，N为根据距离间隔切割出来的片段的数量，使用评估函数对每个点hk∈Hi进行打分得到c。

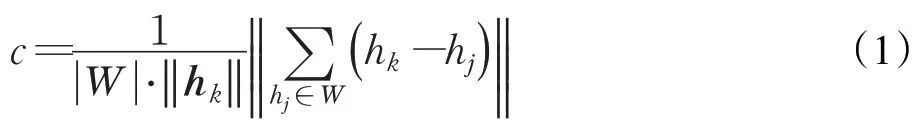
式中，W指hk当前所在的滑动窗口。将得分c大于阈值的点保存下来，记录为待筛选的特征点。

2.2 特征点的筛选

在特征点的粗提取中得到的特征点包括直线的端点，噪音所引起的局部噪点，两段线段相交形成的角点。在三类特征点中，两段线段相交形成的角点仅与实际环境有关，这正是所寻求的稳定特征点，其余两类都属于不稳定的特征点。

通过实验可知，由于雷达在机器人的运动过程中，对直线往往只能观测到其一部分，这时候直线的端点会被算法识别为特征点，其产生的端点在地图上的位置与当前雷达所处的位置有直接的关系。另一方面，由于雷达本身的数据是自带噪声的，当特征点提取的窗口范围内的噪声比较大时，算法容易将一段实际是光滑的平面识别为特征点，其产生的特征点与雷达观测到这段平面的相对位姿和雷达自身的工作情况有关。这两类特征点在建图过程中都会呈现出一种极度的不稳定性，因此需要过滤掉。

为了筛选出稳定的特征点，提出了向量特征点（vector feature points，VFP）。VFP主要通过当前特征点与其附近的点共同形成一个角，通过判断角的两边是否符合条件以及角度是否满足条件，从而达到筛选的目的。筛选的效果如图3所示。

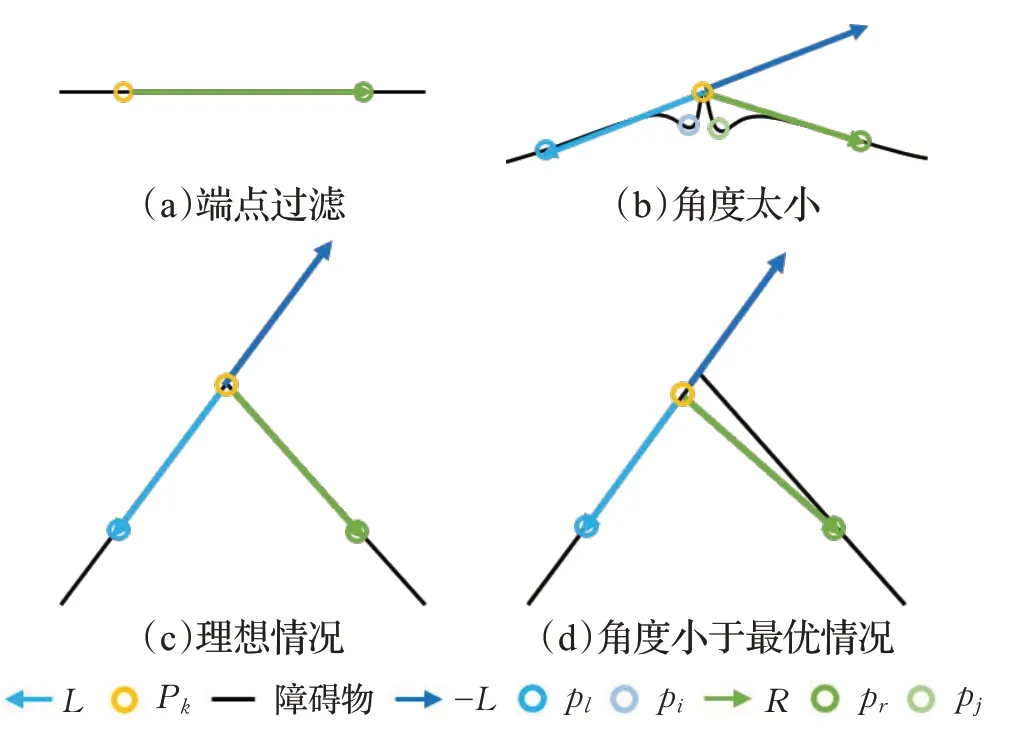
图3 特征点筛选示意图Fig.3 Schematic diagram of feature point filtering

将待筛选的特征点记作pk∈P，寻找距离pk最近的特征点pl，pl∈P，l＜k，||pk-pl||＞tneigh，以及点pr,pr∈P,r＞k,||pk-pr||＞tneigh，这里tneigh为距离参数，主要是为了算法的稳定性，保证不要采集到太近的点。如果在符合要求的范围内找不到pl或者pr时，便舍弃这个点，如图3（a）所示。再对所有点pi,l＜i＜k,pi∈P，以及点pj,k＜j＜r,pj∈P分别计算到向量：

和向量：

的距离：

如果所有的di、dj都小于一定的值，则计算向量-L和R之间的夹角a：

当夹角a大于一定的值时，将pk保存为当前帧的特征点。当角度过小时则舍弃，如图3（b）所示。最终当前帧所剩下的特征点如图2（c）所示。

由于雷达扫描到的数据是离散的，不能够保证每次扫描同一个障碍物时，所提取出来的特征点都是同一个，所以需要根据角度a保存下邻域内最大的特征点。当雷达的扫描情况不够理想时，所计算出来的角度a会比理想情况下的小，如图3（c）、（d）所示。

当所有的数据处理完成之后，将当前帧的特征点加入到地图的特征点数据库Pmap中，再对数据库中的点，根据特征点的夹角a进行非极大值抑制（non maximum suppression，NMS），可以保证当计算出与数据库中已有的点近似的特征点时，只保留下一个效果最好的，如图2（d）所示。

本文所提出的特征点提取算法运行效率非常高，时间复杂度为O(n+m2)，这里的n为一帧雷达的点数量，m为数据库中已经有的特征点数量，同时提取的特征点非常稳定，为后续的匹配算法提供了较好的基础。具体的特征点提取算法可以表述如下：

考虑到SLAM算法在构建较大的全局地图时会对地图整体做优化，导致地图与特征点生成的时候不一致。针对这种情况，可以通过保存关键帧信息与轨迹的方式，根据优化后的轨迹，重新通过本算法离线生成特征点，此时，新生成的特征点将与地图一致。

3 特征点匹配

3.1 全局特征描述子

本文通过将局部地图中的特征点与全局地图中的特征点进行匹配，根据两者间的匹配关系，通过使用RANSAC算法求解出全局地图到局部地图的转换关系Tξ，从而求解全局定位问题。本文提出的匹配算法基于这一事实：当机器人运行着同一个算法在不同的时刻经过同一个环境两次时，两次所构建的地图应该十分相似，记局部地图特征点为集合Plocal={plocal,i}i=1,2,…,M，全局地图特征点为集合Pglobal={pglobal,j}j=1,2,…,N，待求解的全局位姿ξ所对应的转换关系为Tξ。此时有关系：

基于这一关系，当Plocal、Pglobal存在：

时，记vlocal,12=plocal,i2-plocal,i1，vglobal,12=pglobal,j2-pglobal,j1则有：

基于式（8）～（10），构建了如下的描述子。首先获取地图特征点，如图4（a）所示。然后对地图特征点取pi∈P，然后计算所有dim=||pm-pi||，i≠m，以及使用式（10）计算向量pm-pi与所形成的夹角aim，角度范围取[0,2π)，如图4（b）所示。记地图特征点数量为M，则每个点pi的描述子可表述为一个长度为M-1的向量desi={(dim,aim,m)}。为了加速后面对描述子的匹配，本算法对描述子desi里的元素按照dim升序进行排列，如图4（c）所示。

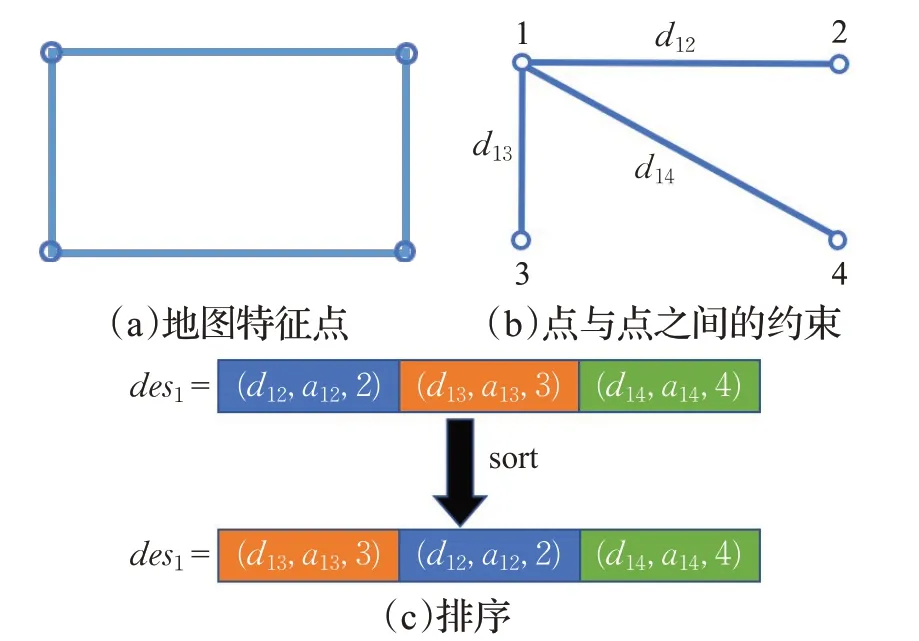
图4 描述子示意图Fig.4 Schematic diagram of descriptor

理论上来说，每一个描述子都包含了地图特征点的所有有用信息，但是为了算法的鲁棒性，当式（7）退化成：

时，算法仍然能够正常工作，对所有的特征点pi都采用了一样的算法得到描述子desi。最终地图的描述子可表示为des=[desk]k=1,2,…,M。除此之外，由于噪声的存在，在不同时间地点采集到的特征点不可能严格意义上的一致，为了解决这个问题，同时提高后续匹配算法的速度，对描述子里面的夹角aim和距离dim进行了离散化处理。

式中，ares和dres分别为所允许的最大角度误差和距离误差，round为四舍五入函数。描述子的生成算法时间复杂度为O(n2+n2lgn)，这里n为地图特征点的数量。具体的算法流程可以表述如下：

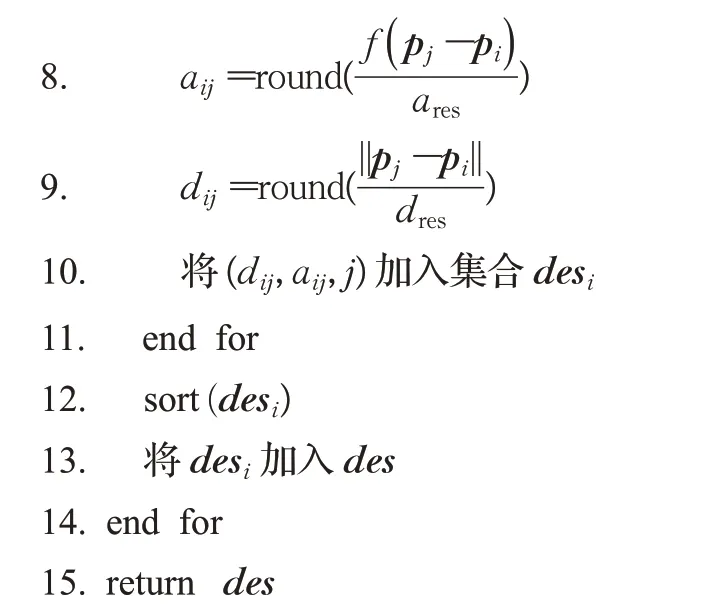
3.2 描述子匹配算法

每一个特征点描述子都包含了与地图其他所有特征点的距离以及两者形成的向量与x的夹角。因此全局特征点之间的约束和关联体现在相应特征点的距离和角度两个方面：一方面，由于距离并不会随着旋转而发生改变，因此当两个特征点相匹配时，必须与足够多的特征点保持着距离一致关系，同时，另一方面，理论上所有距离一致的点之间的角度差值将是相等的，这是由于该角度仅与局部地图和全局地图之间的相对旋转相关，且所有差值都与所旋转的角度相等。因此，可以通过统计所有距离一致的匹配点之间角度的差值，选取数量最多的差值所对应的匹配关系，此时即可完成两个描述子的匹配。

特征点的数量越多，相互之间的约束会变多，从而鲁棒性增强。当环境发生变化，或者噪音影响时，会出现一些原本不存在的特征点或者漏掉一些原本存在的特征点，这些将有可能导致错误的匹配关系。但是当因噪声而产生的新特征点数量少于局部地图与全局地图特征点交集的数量时，算法依旧能够有效消除噪音所带来的影响，因为算法本质上是让能够完成距离一致约束的特征点对自动投票出一个最优结果，当最优结果所得的票数大于一定阈值时，便认为这个结果是有效的。

描述子的匹配过程如图5所示，首先取局部地图的任意一个描述子deslocal,i={(dlocal,im,aim,m)}，与全局地图的任意一个描述子desglobal,j={(dglobal,jn,ain,n)}，根据式（9），首先按照距离一致的关系，给deslocal,i里的每个元素(dlocal,im,aim,m)找到desglobal,j里面匹配的元素(dglobal,jn,ajn,n)，然后通过角度差值相等关系进行角度匹配。如果相匹配元素里面角度差值为amax的元素对最多，则有：

图5 两个描述子匹配过程示意图Fig.5 Matching process of two descriptors

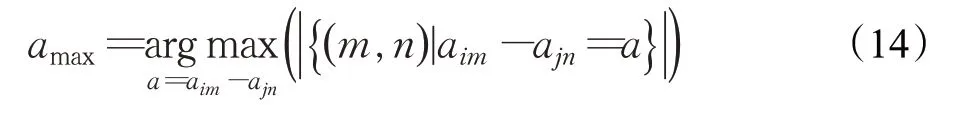
如果角度差值为amax的元素数量超过一定的阈值，那么认为满足这个约束的点对为匹配的点对(m,n)。

任意两个描述子的匹配时间最优情况下复杂度为O(m+n)，最差情况下复杂度为O((m+n)n)，m、n分别为两个描述子的元素数量，算法可以表示如下：

3.3 朴素匹配算法

由于每个地图里面的特征点同时都与其他的特征点产生了联系，建立了点与点之间的约束，所以当将局部地图中的一个描述子与全局地图中对应的描述子成功匹配后，即可得到所有特征点对之间的匹配关系。提出了一种朴素匹配算法（Naive match algorithm，NMA），实现了多个特征点与多个特征点的同步匹配，极大地提高了匹配精度和匹配速度。NMA算法的思路如图6。

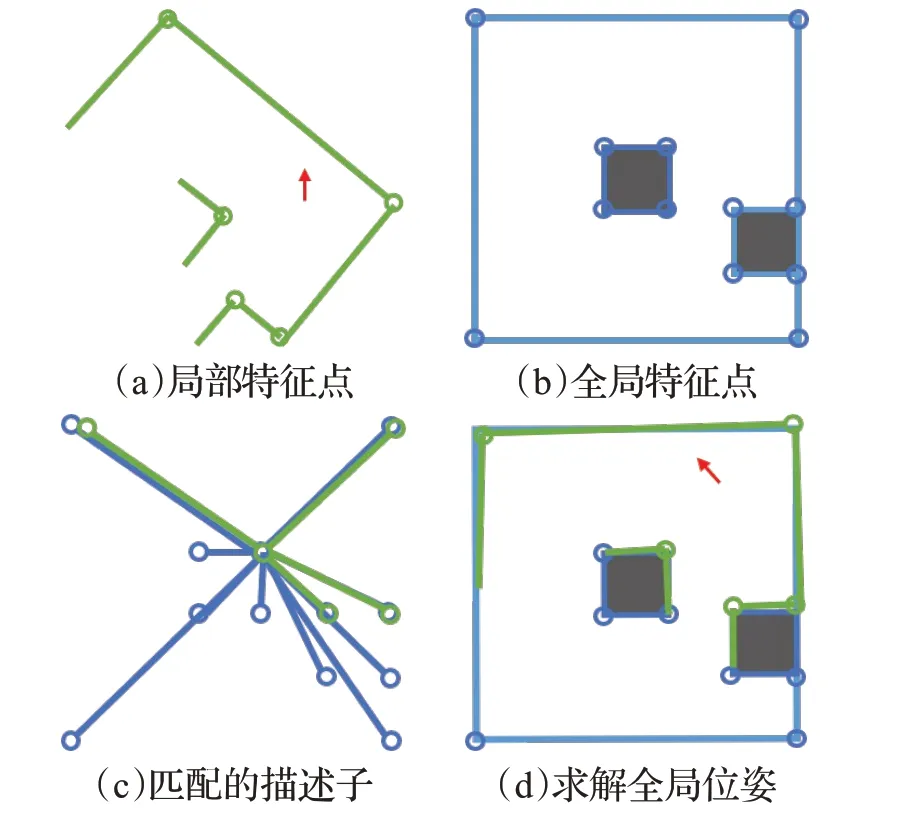
图6 求解全局位姿示意图Fig.6 Schematic diagram of global localization

记Plocal为局部地图特征点集合，如图6（a）所示；Pglobal为全局地图特征点集合，如图6（b）所示，记deslocal,i与desglobal,j完成匹配后所产生的匹配点对集合为matchij={(m,n)},pm∈Plocal,pn∈Pglobal，为了保证匹配算法的鲁棒性，对所有的deslocal,i与desglobal,j都进行匹配，记所有的匹配结果为match={matchij}，最终选取一个匹配对数最多的结果，如图6（c）所示。

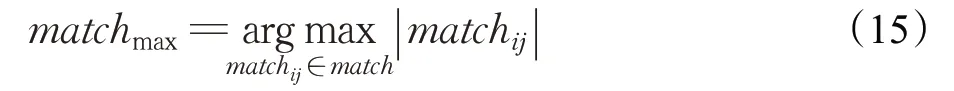
在获得了匹配的特征点matchmax={(m,n)},pm∈Plocal,pn∈Pglobal后，将点对代入模型：

然后通过RASAC算法求解两个点集之间的转换关系Tξ，将局部地图在全局地图里的位姿乘上机器人当前在局部地图里面的位姿Tlocal，即可得到机器人全局定位的结果，如图6（d）所示。

通过完成匹配后，可以得到一个比较理想的全局定位结果。当需要更高精度的定位结果时，可以将当前的定位结果当作初值，然后通过迭代最近点（iterative closest point，ICP）算法，将当前雷达帧的数据和全局地图进行匹配，即可收敛到局部最优值。当初值比较理想的时候，此时的局部最优值便是全局最优值。

3.4 随机匹配算法

由于每一个匹配成功的描述子理论上都包含了所有的可匹配的点对，为了降低计算耗时同时取得一个与NMA在多数情况下一致的表现，本文在NMA的基础上又提出了随机匹配算法（random match algorithm，RMA），用随机的方式完成描述子之间的匹配。

NMA将所有的局部地图特征点集合Plocal和全局地图特征点集合Pglobal进行匹配，并在所有匹配成功的结果中选取了一个最好的结果。由于每个特征点所对应的描述子是由地图上所有的特征点共同形成的约束所组成，每个完成匹配的描述子都会同步地完成局部地图与全局地图的交集中的所有特征点的匹配。当Plocal是Pglobal子集，即符合式（7）时，每个描述子所匹配的结果都将一致。实际上NMA需要穷举所有匹配结果，正是因为局部地图的特征点仅仅与全局地图存在交集，而不是其子集，即当式（7）退化成式（11）时，这导致了每个描述子匹配的结果不一定一致。处于交集中的任意特征点所对应的描述子完成匹配时，其结果将是一致的，同时是最好的。因此，如果能够选中局部地图中处于交集中的特征点，并且将之与全局地图的所有描述子进行匹配，那么其匹配结果将与NMA一致。RMA正是基于这一思想，采用了随机抽取局部地图的特征点所对应的描述子与全局地图的所有描述子进行匹配的方法。只要抽取的次数足够多时，便能够保证抽取到交集中的特征点所对应的描述子。

记局部地图特征点的数量为Nlocal=|Plocal|，全局地图特征点数量为Nglobal=|Pglobal|，两个点集的交集数量为N=|Plocal∩Pglobal|，让匹配的成功率不低于p，所需要采样的次数记为k，可得：

4 实验结果

4.1 实验环境

本文的所有实验都在处理器型号为i5-6300HQ 2.30 GHz，操作系统为Ubuntu 18.04的电脑上运行，算法通过C++程序语言实现，实验基于机器人操作系统（robot operating system，ROS）进行。

4.2 特征点提取算法测试

在本节测试中，主要对特征点提取算法进行测试。测试的方式为构建一个仿真的地图，然后生成雷达数据，同时使雷达数据带上不同程度的噪音，用本文提出的特征点提取算法VFP，与HARRIS特征点、ORB特征点和LOAM里面所提出的特征点提取算法进行对比。主要对比这些算法在不同程度噪音下的精确率（precision）、召回率（recall）和运行耗时（ms）。本次所使用的地图如图7（a）所示，地图的分辨率为0.02 m，长度为10 m，宽度为10 m。雷达的角分辨率为0.25°，扫描范围为360°，放置在地图x=7.5 m，y=5 m的位置。三次测试数据使用的噪音标准差分别为0、0.03和0.07。为了保证算法结果易于观察，同时量化指标，对多种算法的识别结果均采用了NMS算法，保证每个半径为1 m的范围内，只保留下响应值最大的特征点。通过将识别出来的特征点距离参考特征点小于0.1 m的特征点记录为正确识别。识别效果分别如图7（b）、（c）、（d）和表1、表2、表3所示。可以发现，HARRIS算法的耗时远超其他算法的耗时，而ORB算法并不适合于这种纹理较为简单的雷达图，导致了其在所有测试中都表现较差。随着噪声程度的加剧，HARRIS、LOAM算法的精确率有了较大程度的下降，同时NMS的耗时大幅度提高，而召回率却只出现较小幅度的下降，这表明这两个算法的抗噪能力比较弱，提取出了较多的特征点，导致NMS的耗时大幅提高，以及精确率下降。

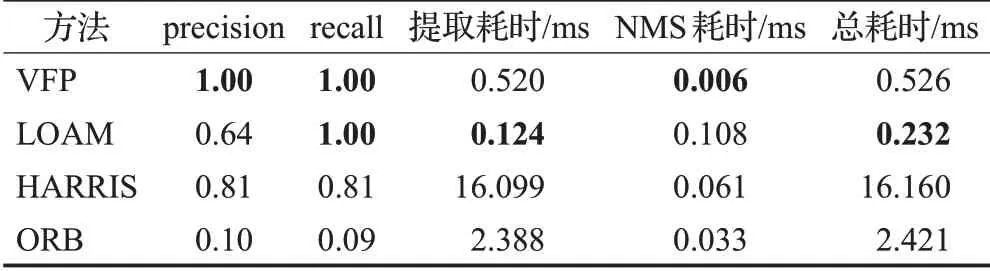
表1 噪声标准差为0时不同算法对比Table 1 Comparison of different algorithms when noise standard deviation is 0

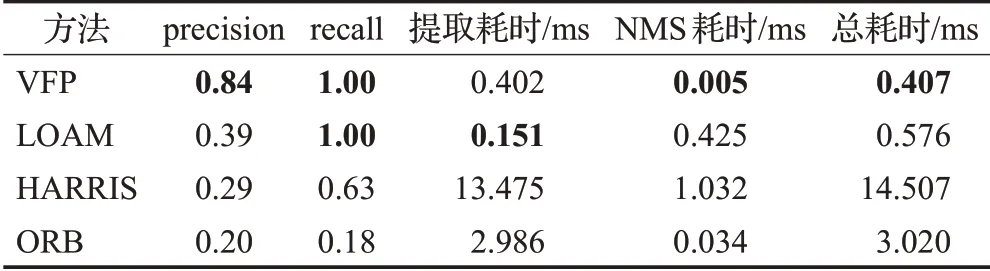
表2 噪声标准差为0.03时不同算法对比Table 2 Comparison of different algorithms when noise standard deviation is 0.03

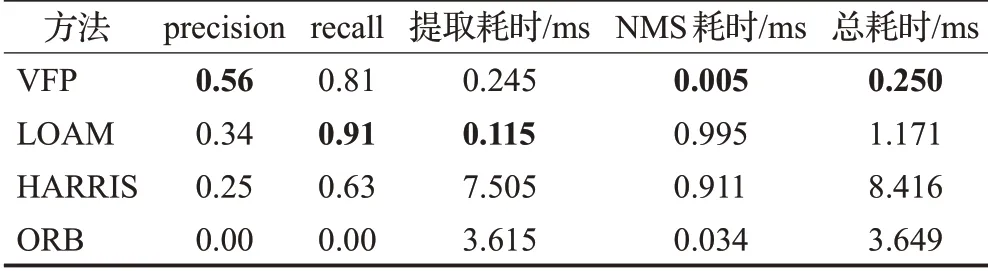
表3 噪声标准差为0.07时不同算法对比Table 3 Comparison of different algorithms when noise standard deviation is 0.07

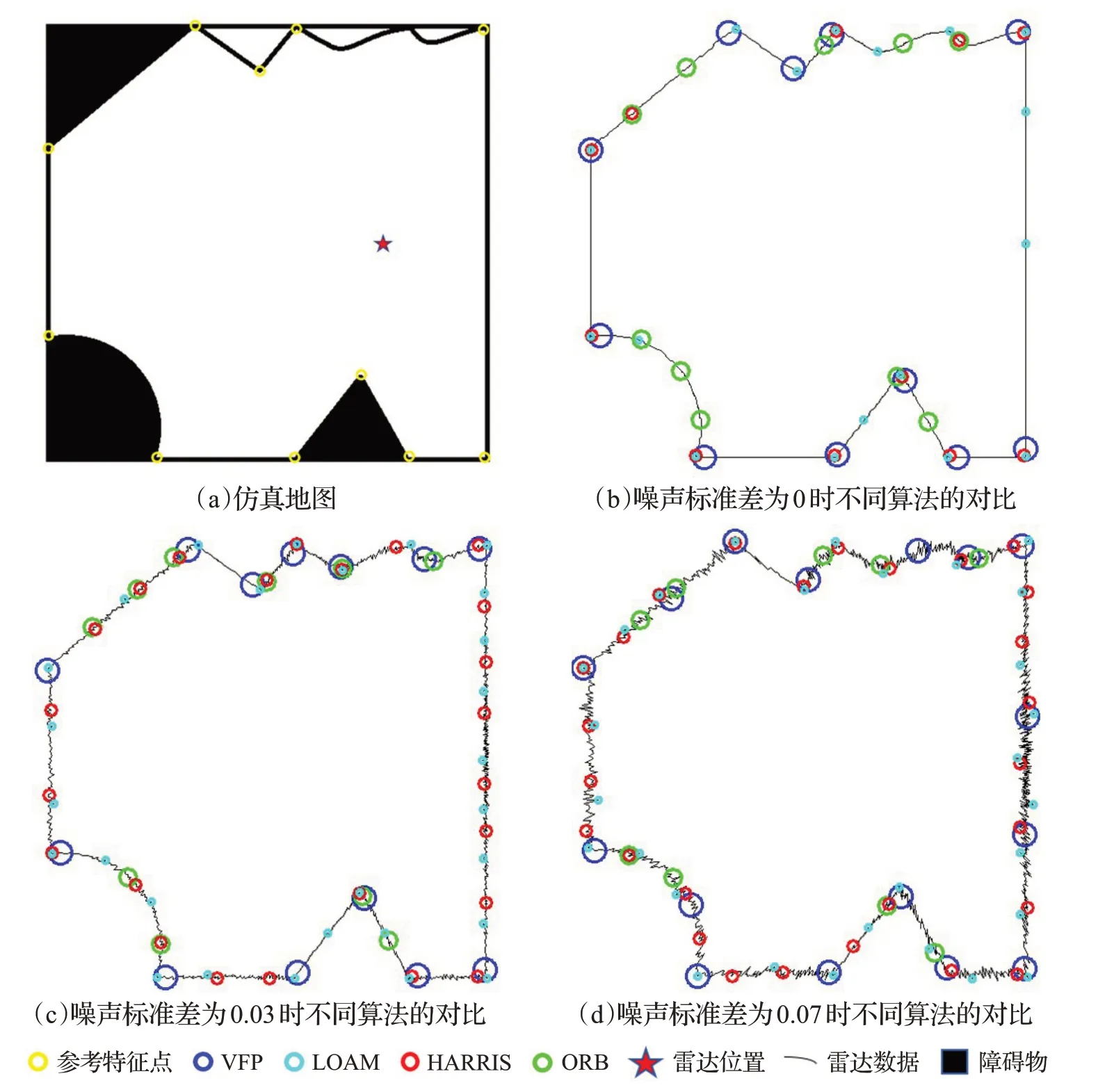
图7 在带噪声情况下不同算法的对比Fig.7 Comparison of different algorithms in the case of noise

在不同程度的测试中，VFP算法的表现最好，在没有在噪音程度较小的情况下，VFP算法的精确率和召回率都能保持在较高的水平，同时总耗时极低。例如，在噪音标准差为0的时候，算法甚至达到了100%的精确率和100%的召回率，在噪音标准差为0.03时，算法准确率稍有下降，而召回率却依然能够保持在100%。这表明VFP算法比较稳定，抗噪能力较强，能够为后续的匹配算法提供一个较理想的描述子；计算资源消耗较低，不会给系统本身造成较大的负担，实时性能够得到保障。

4.3 匹配算法的计算性能测试

在本节测试中，主要是对匹配算法的计算性能进行测试。测试的方式为用程序随机生成足够多的地图特征点，模拟全局定位的真实情况，统计算法的实时计算耗时。对全局地图特征点数量50、100、200和300个点分别进行了局部地图特征点数量从0到49、99、199和299个的朴素匹配算法和随机匹配算法的耗时统计，随机匹配算法参数为，结果如图8所示。可以看出，在当前参数下，在任何规模的数据量下随机匹配算法的时间消耗都少于朴素匹配算法。并且，随着数据规模的增大，随机匹配算法的运行速度优势越来越明显，同时两者在大于95%的情况下，两者取得的结果是一致的。虽然朴素匹配算法能够严格意义上的找到全局最优匹配，但是与随机匹配的算法的性能差距较大，并且在实际运行过程中，算法以非常高频的运行，使用随机匹配算法在绝大多数的情况下能够实时取得一个理想的结果。

图8 匹配算法消耗的时间Fig.8 Time cost of matching algorithm

可以观察到，不管是朴素匹配算法还是随机匹配算法随着局部特征点数量的增加计算的耗时都呈现出增加的趋势。对朴素匹配算法而言，这主要是由于匹配次数和单次匹配所需的时间的增加；对随机匹配算法而言，匹配的次数会保持稳定，然而单次匹配所需要的时间会大体上呈现出线性增长。

4.4 在不同场景下的定位效果

在本节测试中，主要对算法在不同场景下的定位效果进行测评。测试的方式为通过在仿真软件GAZEBO中搭建一个虚拟的世界，并且运行本算法。本次测试的所使用的场景为长25 m、宽25 m，所使用的雷达角分辨率为0.25°，扫描范围为180°。测试场景主要有静态环境、发生了一定变化的动态环境以及具有相似子结构的场景。

静态场景下的测试结果如图9所示，在机器人自转一周之后，采集到了足够多的特征点时，算法完成了匹配。这是由于在这个场景中，机器人刚好处于一个比较理想的位置，且实时运行的时候场景与建图时完全一致，当采集到的特征点数量满足所设置的阈值时，算法便能完成全局定位任务。

图9 静态环境下的全局定位效果Fig.9 Global localization in static environment

动态场景下的测试结果如图10所示。通过在运行全局定位算法之前，把多个原本不存在的物体摆放在机器人的启动位置附近，以及把机器人摆放在一个比较差的初始位置，此时便不能够像静态场景中一样理想，快速完成全局定位任务。由于机器人启动位置附近，干扰物较多，同时特征点数量较少，机器人必须移动，直到采集到足够多的特征点。当机器人采集到足够多的特征点时，算法同样能够完成全局定位任务，如图10（b）所示。

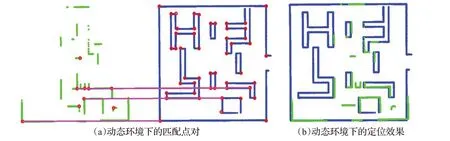
图10 动态环境下的全局定位效果Fig.10 Global localization in dynamic environment

相似环境下的测试结果如图11所示。由于场景本身有比较多近似的局部区域，如果设定的匹配点阈值较低时，算法容易产出误匹配，如图11（a）、（b）所示。但是随着机器人的运行，采集到的特征点越来越多，它们之间所形成的约束更加复杂时，算法便能够有效过滤掉局部相似的所带来的影响，成功实现全局定位，如图11（c）、（d）所示。

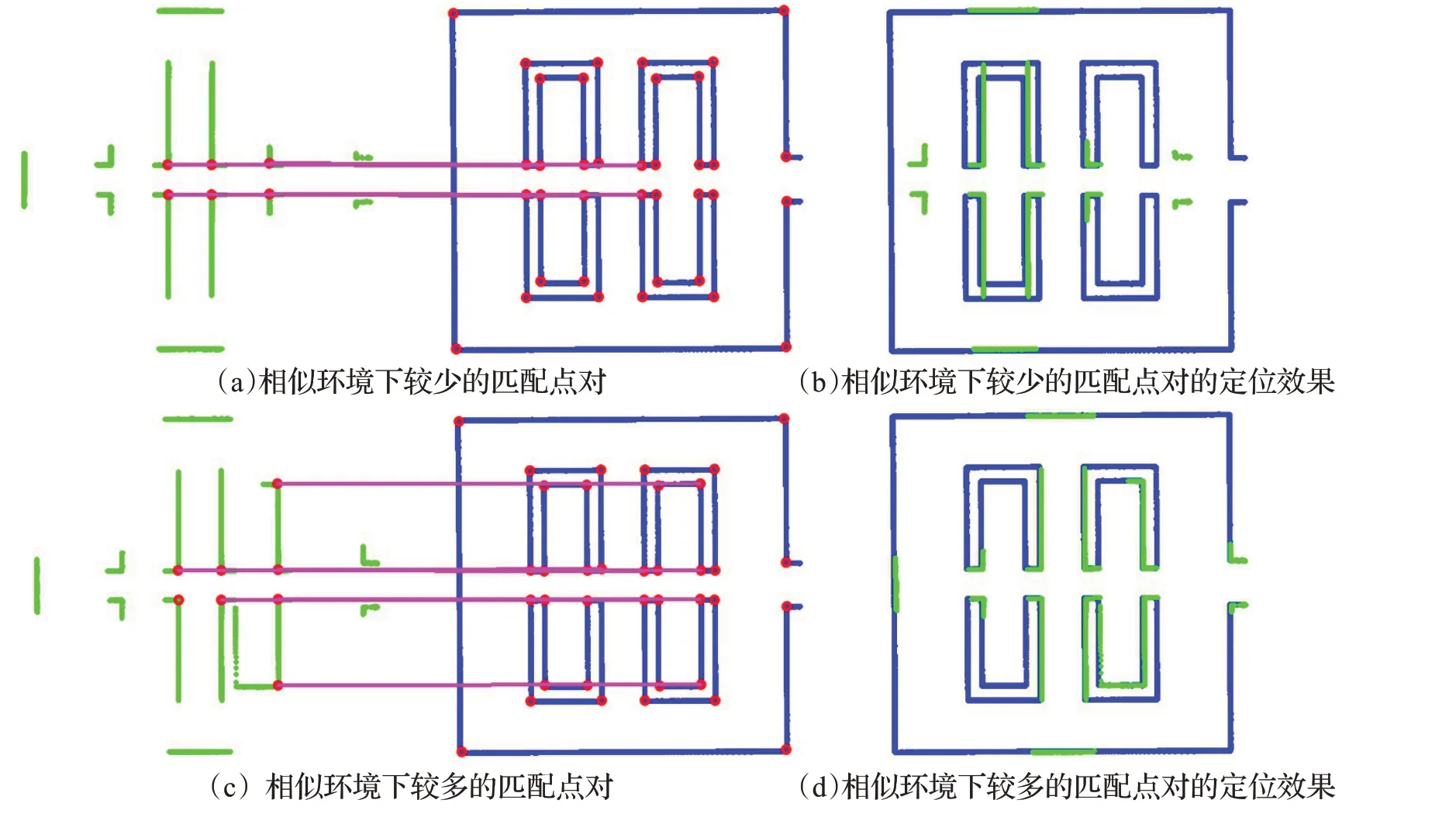
图11 相似环境下的全局定位效果Fig.11 Global localization in similar environment

4.5 定位效果对比实验

本节主要是为对算法在实际场景下的全局定位效果的测试。测试的方式为，在Deutsches Museum Dataset[12]和Mit Stata Center Dataset[18]上分别运行了RMA、AMCL和Cartographer三个算法。测试的具体方法为，首先针对数据集，通过Cartographer构建全局地图，然后将这个全局地图用于全局定位。实验分别在同个场景、不同时间所采集的数据集上选取了4个不同的时间、地点作为全局定位算法的启动位置，然后通过统计成功实现全局定位时机器人从上电到当前的时间，以及每一帧的平均耗时和定位成功时的精度。由于这两个数据集的场景都比较大，为了尽可能地定位成功，将AMCL的粒子数量设置为20 000；将Cartographer的搜索层数设定为7层，搜索窗边长为7 m，搜索角度设置为30°。

全局定位所需要的运行时间如图12所示，可以看出，在Deutsches Museum Dataset上，本文提出的算法所需要机器人运行时间明显更少，而AMCL在地点3甚至无法在规定的时间（180 s）内完成全局定位。在Mit Stata Center Dataset数据集上，可以看出本文的算法都能够在规定的时间内完成全局定位算法，与AMCL算法对比，机器人运行时间相近，而Cartographer则无法在规定的时间内在地点2、3和4完成全局定位。

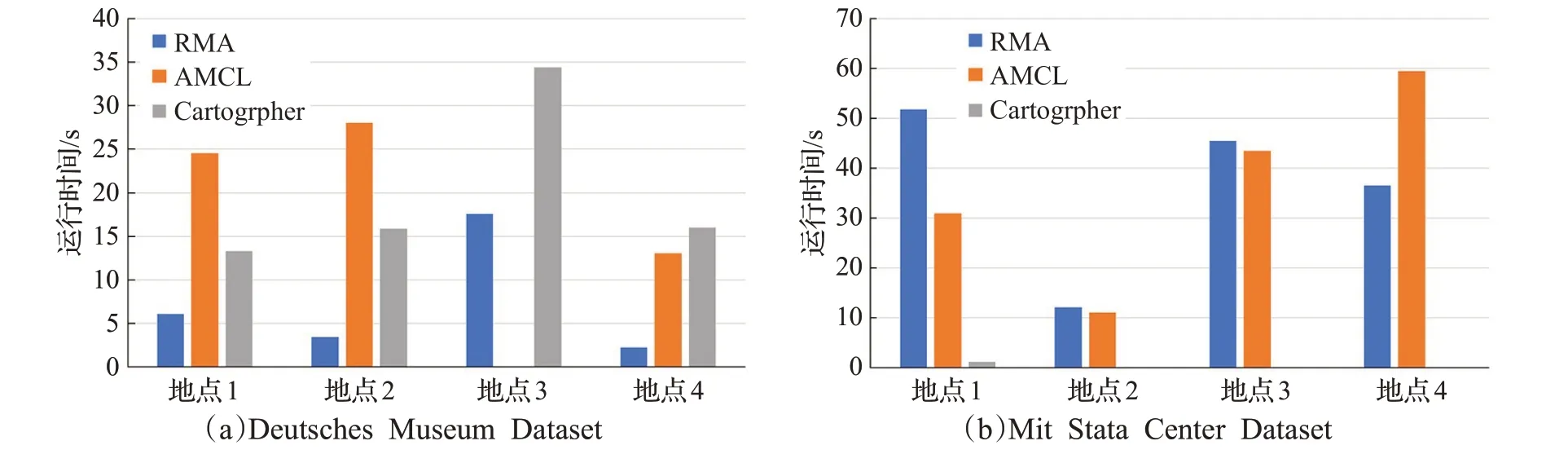
图12 全局定位所需的运行时间Fig.12 Runtime required for global localization

平均每帧耗时和定位精度如表4、表5所示，可以看出RMA算法平均每帧运行所需要的时间远低于AMCL和Cartographer算法。在定位精度上，三者的精度较为接近，此时的主要误差来源于雷达本身数据的噪音和栅格地图分辨率的限制。算法的全局定位效果如图13所示，可以看出，本文所提出的算法可以很好地完成全局定位。

表4 在Deutsches Museum Dataset上不同算法对比Table 4 Comparison of different algorithms on Deutsches Museum Dataset

表5 在Mit Stata Center Dataset上不同算法对比Table 5 Comparison of different algorithms on Mit Stata Center Dataset

图13 全局定位的实际运算效果Fig.13 Global localization in real world

5 结论

本文提出了一种基于全局特征点匹配的移动机器人全局定位算法。一方面设计了一种高效稳定的特征点提取算法，另一方面建立了全局所有特征点之间的相互关联和约束，并且基于这些关联和约束，采用高效的随机匹配算法，同步完成了多个特征点对的匹配，大大提高了算法的稳定性。在运算性能方面，算法总体维持在了一个较低的复杂度和运算时间，在效果上，与AMCL和Cartographer算法对比，全局定位的效果在多数情况下更优。