数据归一化方法综述

杨寒雨，赵晓永，2，王 磊

1.北京信息科技大学 信息管理学院，北京 100129

2.北京信息科技大学 北京材料基因工程高精尖创新中心，北京 100129

如今的大数据场景信息非常丰富，从物联网到智能城市，再到医疗保健、社交媒体和金融应用。大数据呈现容量大、种类多等特点，大规模且杂乱无章的数据会对研究结果产生巨大的影响[1]。大数据因其高价值的特征，可以作为机器学习的输入以预测未来趋势[2]。在机器学习任务中，对大数据应该进行规范化的预处理，从而提高模型的预测精度[3-4]，获得机器学习的高性能[5]。数据归一化是数据预处理的一个重要步骤。

归一化（normalization）是一种简化计算的方式。即将所有属性以相同的测量单位表示，并使用通用的刻度或范围。归一化试图赋予所有数据属性同等的权重，使属性之间的比较与聚合更容易，数据的收敛条件更好[6]。不会出现属性值凌驾于其他属性值之上的情况。另一方面，归一化有助于防止使用属性之间距离度量的机器学习算法产生扭曲的结果，并提高了数据分析的效率。常用的归一化方法有Min-Max、Z-Score和Sigmoid等。

归一化在当今数据应用的不同方面都有深刻影响[7]。在深度学习方面，由于深度学习是包含很多隐藏层的神经网络结构，在训练过程中，各层参数在不停变化，所以会存在内部变量偏移（internal covariate shift）[8]。在基于机器学习的分类任务中，应用了Min-Max数据归一化技术的随机数森林和决策树模型的平均准确率最高可达到99%[9]。在股指价格变动预测任务中，选取合适归一化方法的支持向量机（support vector machine，SVM）可以提高预测准确率2.4%[10]。同时，归一化在数据流挖掘方面同样重要。不同评价指标往往具有不同量纲，数值间差别较大，不进行处理可能会影响到数据分析的结果[6，11]。为消除指标之间的量纲和取值范围差异的影响，需要对输入数据进行归一化处理。将其按照比例进行缩放，落入一个特定的区域，以便进行综合分析[12]。例如将人的身高属性值映射到[-1，1]或[0，1]内。而在流式数据场景下，处理的是非连续的数据，数据以流的形式先后到达训练点，一次一个样本，所以流处理方法必须在时间和资源的严格限制下处理数据[13]。这就为流场景下数据的归一化带来了极大的挑战性。

目前，国外对归一化问题的研究很多。比较著名的有Google（谷歌）、Texas Tech University（得克萨斯理工大学）等。但当前研究仅仅侧重于神经网络隐藏层之间的归一化算法，包括文献[8，14-15]等，缺乏流场景下综述类文献。目前国内较为详尽的归一化综述为文献[16]，此文献着重于深度神经网络下隐藏层之间的批数据归一化算法。本文则系统地整理并分析了相关文献，提出基于批数据的归一化分类方法以及基于流数据的归一化分类方法，通过上述方法对近年来的研究进行了综述，并讨论了未来研究方向。

1 数据归一化的基本方法

1.1 输入层的数据归一化方法

数据集的数据对学习建模不是完全有效。有时直接选定的属性是原始属性，仅在获取它们的原始域中具有意义，不足以获得准确的预测模型[6]。机器学习应注意输入数据属性的统计分布，且检查属性统计的变化[17]。

因此，需要对数据执行一系列预处理步骤以实现将原始属性转换成能利用的属性，这将有助于模型的建立。线性无量纲方法可用于批数据在不同学习模式中在输入层的归一化操作。詹敏等[18]根据线性无量纲化方法函数构成所使用的中心点值和值域指标，对线性无量纲化方法进行分析总结；郭亚军等[19]在多种线性无量纲化方法的基础上，就指标无量纲化过程的稳定性问题提出了改进型方法理论；郑宏宇等[20]讨论了综合评价中线性无量纲方法的选择问题。

表1列出了批数据与流数据分别在学习模式和处理阶段两方面的归一化方法的对比。对于流数据在离线学习下的归一化操作，可通过将流数据转为批数据从而选取与批数据在离线学习下相同的归一化方法。而对于批数据在在线学习下的归一化方法，可通过海量批数据的方式以采用与流数据在在线模式下相同的归一化方法。

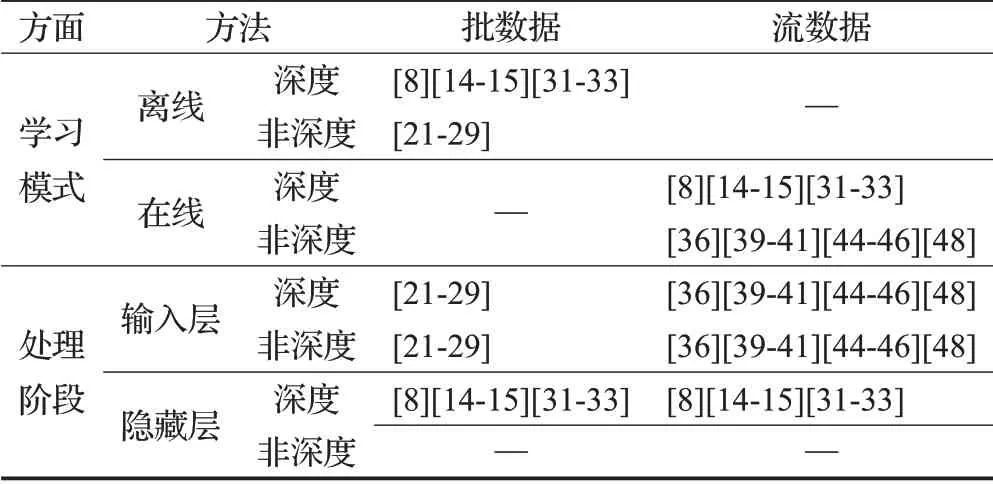
表1 数据归一化方法对比Table 1 Comparison of data normalization methods

在本节中，重点介绍将数据的原始分布转换为目标数据分布的一系列线性无量纲方法。

1.1.1 Min-Max

Min-Max归一化[21-24]也称为线性函数归一化，对原始数据做一次线性变换，通过以下函数（1），将原数据映射到[0，1]之间，不改变原始数据分布。函数（1）中，拟归一化数据用x表示，xnew则为x归一化后的数据，Max、Min分别表示为当前数据中最大值和最小值。

优点：对原数据做处理之后并不改变数据分布。

缺点：过度依赖最大最小值，当有异常数据点出现时会对结果产生较大影响。

1.1.2 Z-Score

Z-Score[21-24]的原理是将原数据处理成符合正态分布的数据，具体是取得数据的均值和标准差，通过以下函数（2）实现归一化操作。此方法对数据的映射没有一个固定的范围，由数据本身均值和标准差决定。函数（2）中Mean表示数据的均值，StandardDeviation表示数据的标准差。

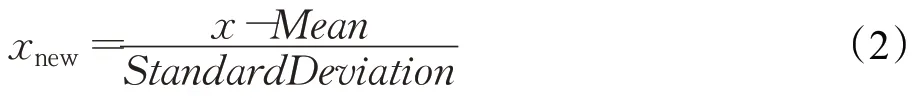
优点：受离群值影响较小，适合最大值、最小值未知的情况。

缺点：改变数据的分布。

1.1.3 Sigmoid

Sigmoid函数也称为Logistic函数[25-26]，值域为[0，1]，经过函数（3），输入的数据被映射在[0，1]之间。Sigmoid函数具体函数图像如图1所示。

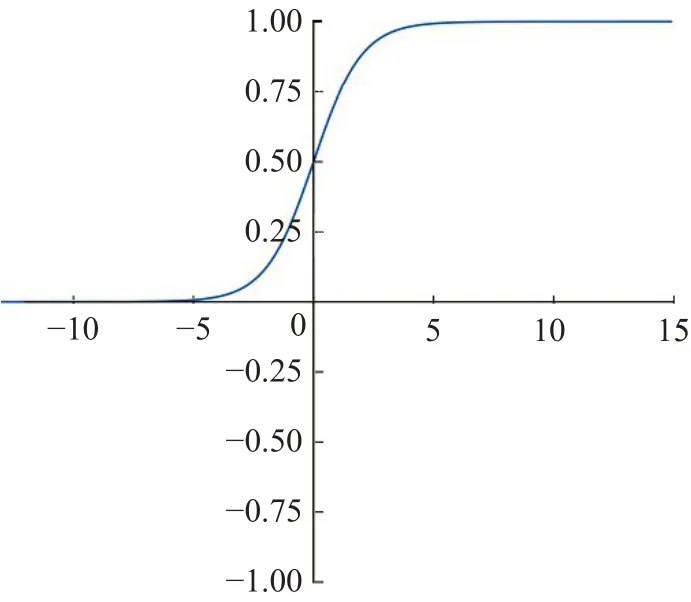
图1 Sigmoid函数图Fig.1 Sigmoid function diagram

优点：适合用于反映二分类结果的概率，对于计算反向传播较为简单。

缺点：可能存在梯度消失问题。

1.1.4 小数定标

小数定标[21-24]通过移动小数点直观地对数据进行处理，将原始数据的绝对值映射到始终小于1的范围内。函数如公式（4）所示，其中j是整个输入数据的绝对值最大的数据的位数。

优点：适用范围广，受到数据分布影响小，更加实用。

缺点：过度依赖最大最小值，容易受异常点影响。

1.1.5 Rank Gauss

Rank Gauss[27]是一种对变量的处理方法，它分为四个步骤。第一步，先对要处理的数据进行排序；第二步，将目标数据转换尺度到[-1，1]；第三步，调整极端值；第四步，使用erfinv()函数，其中erfinv(1)等于正无穷，erfinv(-1)等于负无穷。erfinv()是erf()的反函数，erf()的值域为[-1，1]，表达式如公式（5）所示。第四步使得归一化后的数据满足高斯分布。

优点：数据变为高斯分布，更为直观。

缺点：只保留了数据的排序信息。

1.1.6 反余切函数

反余切函数的值域为[0，π]，函数表达式如公式（6）所示，值域范围为[0，1]，归一化后的数据映射到[0，1]之间。同时也有研究人员提出基于反三角函数的非线性预处理方法[28]。

优点：函数图像平稳，对于计算反向传播较为简单。

缺点：仅当数据都大于等于0时，映射的区间为[0，1]。并非所有数据标准化的结果都映射到[0，1]区间上。

1.1.7 tanh

tanh函数[29]值域为（-1，1），经过此函数数据被映射在（-1，1）之间，其中tanh函数的表达式如公式（7）所示。图2为tanh函数具体函数图像。

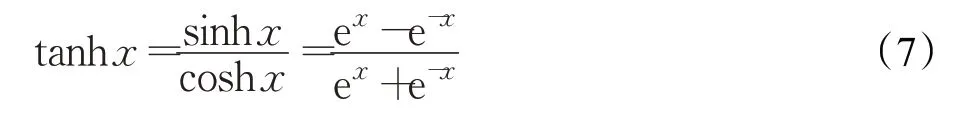
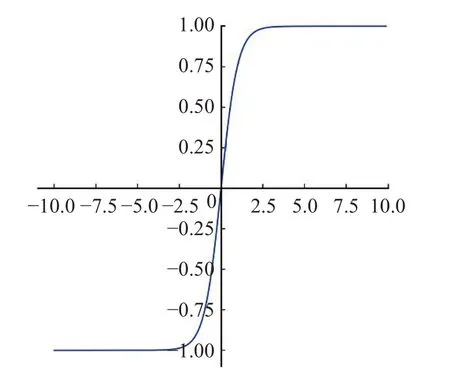
图2 tanh函数图Fig.2 tanh function diagram

优点：训练容易。

缺点：全部激活，使得神经网络较重（heavy）。

1.2 隐藏层的数据归一化方法

当批数据进入深度神经网络后，容易出现“Internal Covariate Shift”的问题。由于深度学习是由多层神经元组成，某一层更新参数，在深度的迭代下，即使参数的变化较小，在多层次的影响下也会对结果产生较大影响[8]。

流数据按顺序先后到达，难以存储在内存中。当前深度学习下绝大多数的隐藏层归一化方法需要在学习任务之前提供整个训练数据集，所以在隐藏层下对流数据进行归一化任务极为困难。而对于流数据下的深度学习应用，Zhang等[30]提出了在线深度学习模型，此模型能够从数据流中连续训练深度学习模型，并且它能够随着时间的推移使模型能力从简单到复杂，很好地结合了在线学习和深度学习的优点。在线深度学习模型中的隐藏层归一化方法可使用深度学习隐藏层中的归一化方法。深度学习隐藏层下有如下六种归一化方法被先后提出。

1.2.1 Batch Normalization

由于低层网络更新了参数，经多层迭代使后面层输入数据发生变化。Ioffe等[8]提出Batch Normalization，中心思想是在隐藏层的每一层输入前加一个归一化层，在数据进入隐藏层前，先进行归一化处理，处理之后再进入神经元进行运算[4]。例如网络第四层输入数据为X4（X4表示网络第四层的输入数据），把输入数据归一化为均值为0、方差为1的数据集，然后再输入至第四层进行计算。

优点：提升训练速度，尤其在计算机视觉任务上表现较好。

缺点：过度依赖批量大小（batchsize）。

1.2.2 Layer Normalization

由于BN（batch normalization）过度依赖批量的大小，当批量较小时，可能由于批量大小太小，均值和方差不具有全局代表性，导致模型效果恶化。Ba等[14]提出Layer Normalization，中心思想是对当前隐藏层整层做归一化操作。与Batch Normalization的不同之处在于，BN是针对同一个样本中的所有数据，而LN（layer normalization）是针对于单个样本来操作。在LN中，一个批里就有与批量大小同数量的均值和方差。均值计算方法如表达式（8）所示，方差计算方法如表达式（9）所示。Batch Normalization与Layer Normalization中均值与方差的不同计算方式如图3所示。

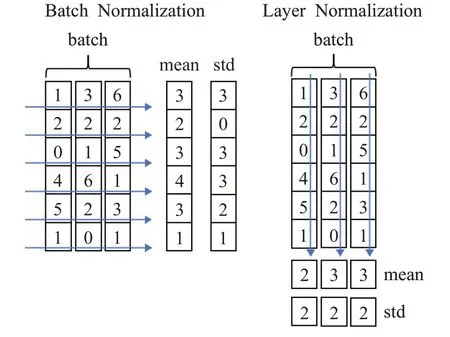
图3 BN与LN对比Fig.3 Comparison of BN and LN

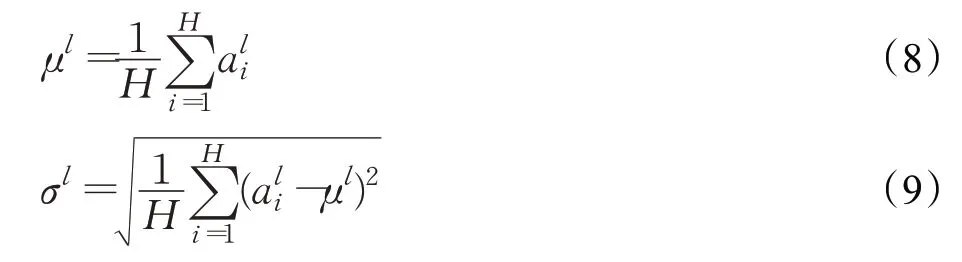
其中H是一层神经元的个数，一层网络共享一个均值和方差，ai表示当前层中第i个神经元。

优点：批量大小较小时，效果好；适用于自然语言处理任务。

缺点：批量大小较大时，效果不如BN。

1.2.3 Instance Normalization

BN针对于对数据的归一化，但对于图像风格化任务来说，应注重于图像实例的处理，Ulyanov等[15]提出Instance Normalization。与BN的不同之处在于，IN（instance normalization）作用于单张图片的单个通道，对此单独进行归一化操作，而BN是对同一个批中的所有图片的同一通道进行归一化。图4具体展示了BN、LN与IN的不同之处，BN是针对所有图片同一通道，LN针对一张图片的所有通道，而IN针对一张图片的一个通道。IN归一化表达式如式（10）所示，其中均值计算方法如表达式（11）所示，方差计算方法如表达式（12）所示。xtijk表示它的第tijk个元素，k和j代表空间维度，i是特征通道（如果输入是RGB图像，则是颜色通道），t是该图像在当前批量中的索引。公式中ε是一个很小的正常量，以防止除0，H、W表示特征图的高和宽。

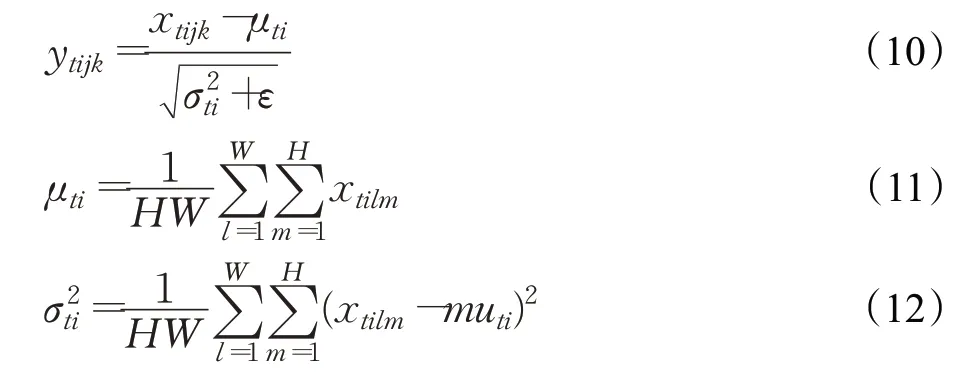
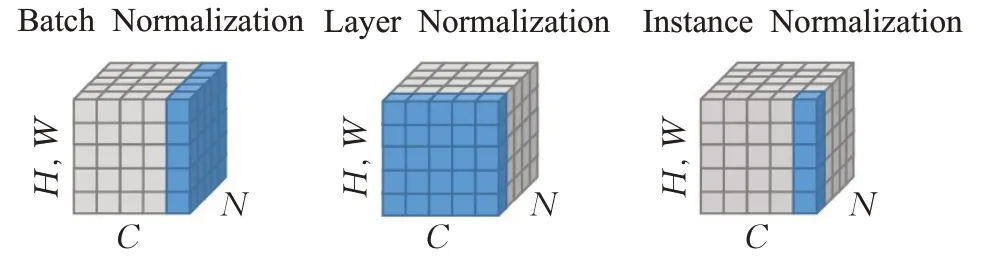
图4 BN、LN与IN的对比Fig.4 Comparison of BN，LN and IN

优点：不受批量大小和图片通道的影响。

缺点：丢失通道之间的相关性。

1.2.4 Group Normalization

在视觉识别任务上，Wu等[31]提出Group Normalization，在GN（group normalization）中，将图片的通道分为不同的组，针对于不同的组来做归一化操作。具体表现为将特征的维度由[N,C,H,W]重新修改为[N,G,C∥G,H,W]，归一化的维度为[C∥G,H,W]，其中G是分的组的数量。

优点：不依赖批量大小。

缺点：当批量大小较大时，性能不如BN。

1.2.5 Switchable Normalization

不同的神经层可能需要不同的归一化操作，而每一层归一化都是由人工设计并操作，这将消耗大量人力。Luo等[32]设计了一个自适应归一化层，通过建立一个通用的归一化层来解决所有问题。主要操作是将BN、LN、IN分别赋予不同的权重并结合，由网络自行学习调整。图5展示SN（switchable normalization）的详细计算方法。

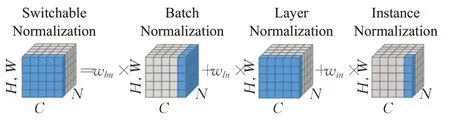
图5 SN计算方法Fig.5 SN calculation method

优点：集BN、LN、GN优点于一身。

缺点：训练复杂。

1.2.6 Filter Response Normalization

谷歌研究所的Singh等[33]提出FRN（filter response normalization）方法，旨在消除批量大小影响的同时也能获得大批量下BN的性能。主要方法是设计一个归一化层，里面包含一个归一层和一个激活层。FRN方法具体框架如图6所示，其中的归一层类似于IN，是对单个图片的单一通道操作的。FRN中v2是x的二次范数的平均值，归一化层需要进行缩放和平移变换，γ和β是可学习的参数。

优点：不受批量大小的影响。

缺点：暂无。

综上，本研究将隐藏层归一化算法的方法与优缺点进行了对比。表2列出了隐藏层归一化方法，从提出原因、方法、优点与缺点四个维度进行具体分析。通过表2可以看出BN主要用于解决内部斜变量迁移的问题。然而BN过度依赖批量大小，为解决此问题，继而研究LN、GN、FRN等归一化方法。当批量大小较大时，BN的效果仍为最优。不同的应用任务应选择不同的归一化方法，BN适用于计算机视觉任务；LN更适用于自然语言处理；对于图像实例应用来说，IN为最佳选择。

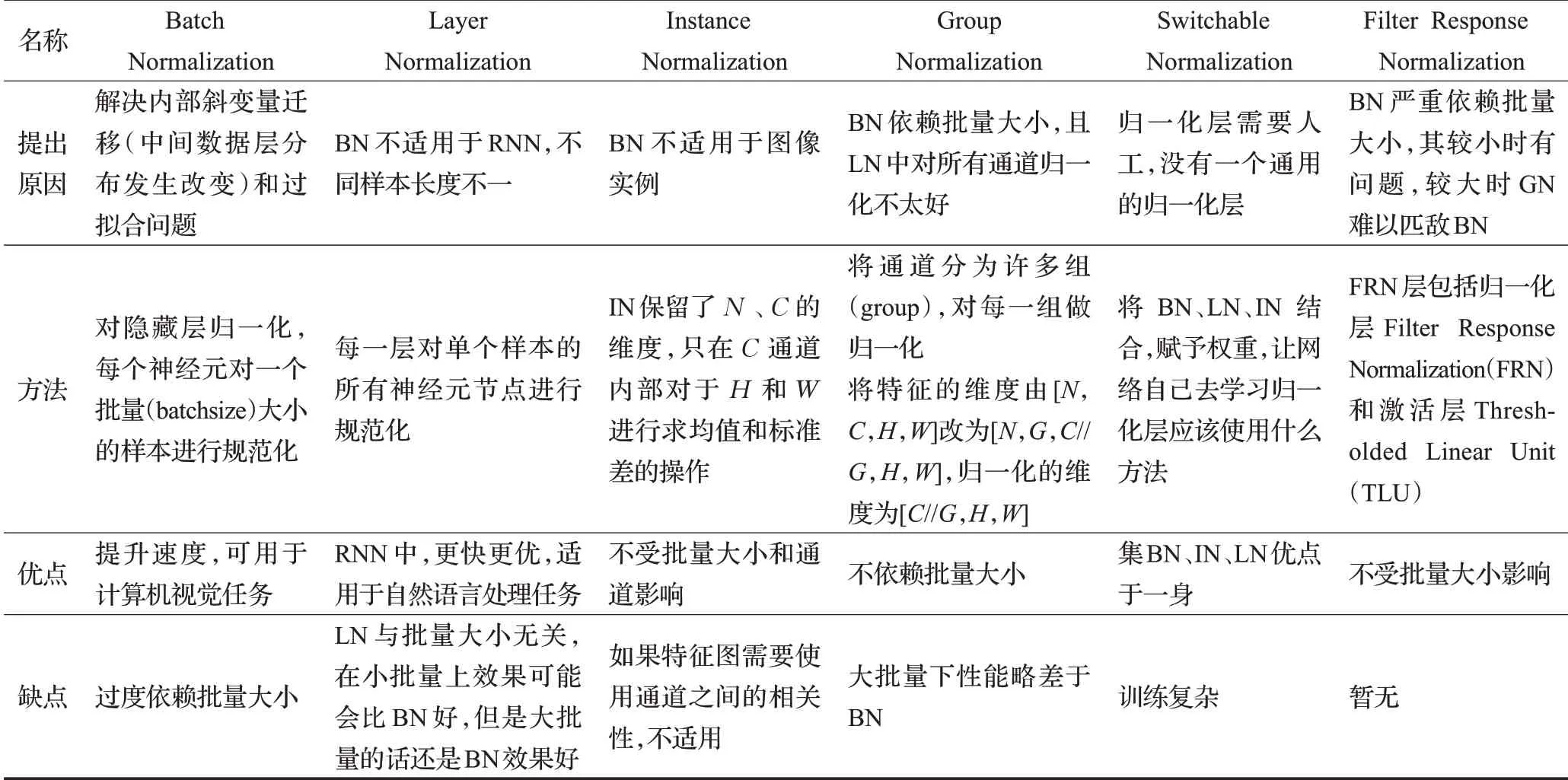
表2 隐藏层归一化算法对比Table 2 Comparison of hidden layer normalization algorithms

2 流数据的归一化法

大数据流具有不断变化的性质，有严格的内存和时间限制以及学习训练前无法获得全部数据的特点，所以大数据流的预处理比批数据更具挑战性[34]。但就目前为止，对于数据流的归一化算法研究较少。预处理数据参数保持固定或手动调整可能导致预测结果不佳[35]。通常采用滑动窗口技术对流数据进行预处理参数调整。窗口的选择对结果至关重要。本章重点从窗口选择及流式数据下的归一化法两方面进行归纳分析。

2.1 窗口

由于流数据以流的形式输入，需要使用滑动窗口或者翻转窗口来暂时存放数据。流场景下，对于窗口的选择也至关重要。

2.1.1 滑动窗口

在流处理应用中，对于数据的传输，通常使用滑动窗口技术。滑动窗口有一个固定的长度或时间长度，不停捕捉随着数据流到来的数据，待窗口内数据被填满（比如收集了5个数据）或满足规定的时间长度（比如到达10 s）后，窗口根据规定的滑动长度向前移动并对窗口内数据进行处理。一般来说滑动长度小于或等于窗口长度，因此窗口是重叠的，相邻的窗口每次都包含一些共同的元素。滑动窗口模型的优点是保持存储空间，从最近的数据点保持新的知识和有效的处理。

图7为滑动窗口模型的示意图。如图所示，定义了一个持续时间为10 s，滑动间隔为5 s的滑动窗口。第一个窗口（W1）包含从0～10 s到达的元素，第二个窗口（W2）包含从5～15 s的元素，每隔5 s，一些元素被添加，一些元素过期。例如在t=15时，e7、e8、e9、e10被添加到窗口，而e1、e2从窗口过期。通过这种方式，所有的元素都被处理，直至流的结束。

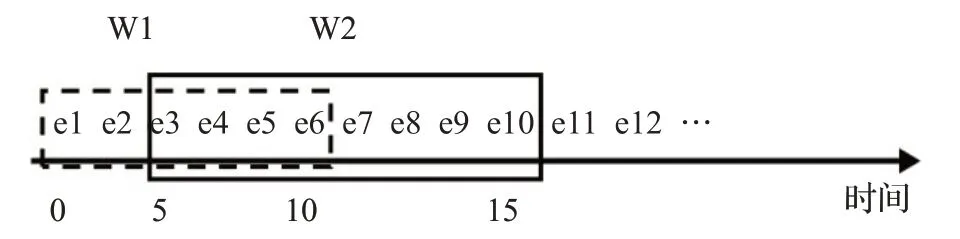
图7 滑动窗口示意图Fig.7 Sliding window diagram

2.1.2 翻转窗口

翻转窗口是滑动窗口的一个特殊形式。与滑动窗口不同的是，翻转窗口没有重叠的窗口，相邻窗口没有共同的元素。窗口的滑动长度或者时间间隔等于窗口长度。在翻滚窗口中，数据的处理都是在一个窗口内进行然后到下一个窗口，中间没有任何重合部分。翻滚窗口收集随着流到达的数据，当窗口长度或时间间隔达到规定长度时，滑动相应的长度到下一个窗口。翻转窗口的示意图如图8所示。

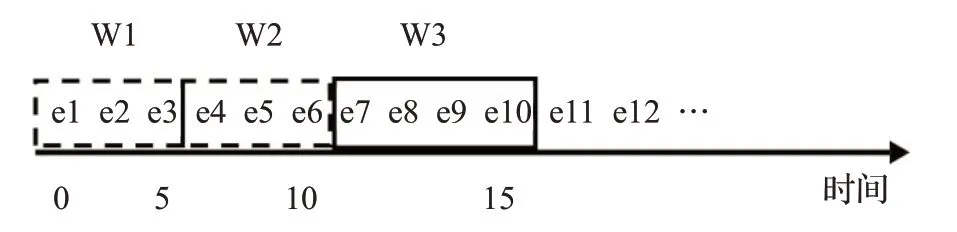
图8 翻转窗口示意图Fig.8 Tumbling window diagram

图8中定义了一个长度为5 s的翻滚窗口。第一个窗口（W1）包含0～5 s的元素，W2包含5～10 s的元素，然后W3包含10～15 s的元素，每隔5 s滑动此窗口，只有新的元素被添加到窗口中，没有一个窗口重叠。例如在t=10时，e4、e5、e6被添加到窗口中，而e1、e2、e3则从窗口中过期。通过这样的方式，整个数据流将被处理。

2.2 流数据输入层归一化方法

2.2.1 Smart Preprocessing for Streaming Data（SPSD）

大多数关于数据流挖掘的研究都将模型再训练和预处理放在一起。但在真实流挖掘情况下，很多时候不需要对模型重新训练，只需要对输入的流数据进行重新归一化的操作。Hu等[36]提出了一种SPSD的方法，该方法有两个重点。

重点一：计算两个指标。

指标一：新的流数据块中至少有一个数据的值在参考的最小-最大值范围样本之外的百分比。目的是将噪音和异常值从数据流的实际变化中分离出来。

指标二：新的样本数据在每个维度的值与该维度的参考最小-最大值之间的最大差异百分比。目的是减少重新规范化的次数，以加快方法的速度。

如图9所示，当前的滑动窗口共有100个数据，其中有95个正常数据，5个异常数据。参考的最大最小值分别为2和-1，指标一的计算方法则为（5/100），假定存在一个值为3的数据x，对于数据x，指标二的计算方法则为[（3-2）/2=1/2]。

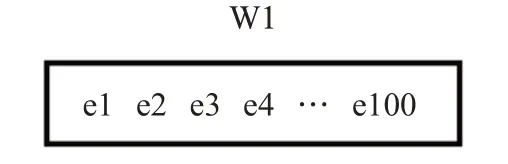
图9 滑动窗口指标计算例子Fig.9 Example of sliding window indicator calculation

重点二：获得指标返回值

算法中自定义两个阈值，若两个指标都超过阈值则返回真（True），反之则为假（False）（True表示重新进行归一化操作，即用更新后的最大值和最小值来对数据块做Min-Max归一化操作；False表示暂时不更新最大最小值，用当前的最大最小值对窗口内的数据进行Min-Max归一化操作）。

SPSD算法分为如下流程：

首先将第一个数据块作为初始的参考数据块，第一个数据块的最大、最小值作为初始的参考最大、最小的范围。

然后进行两个指标计算，获得指标返回值，进行Min-Max归一化，将归一化后的数据发送到基础学习模型中进行分类。当前的这个数据块则会取代原参考数据块成为一个新的参考点，更新后的最大、最小值也将成为参考的最大最小范围。

优点：减少模型再训练的次数，降低新模型生成的成本。

缺点：某些时候效率与重新的模型再训练相比会较低。

2.2.2 特征直方图

在网络安全方面，对于入侵检测等应用，必须注意实时性，及时做好防护[37]。数据处理的操作大部分选择在网络边缘的边缘端进行，处理之后形成适用于数据分析的样式[38]。

Lopez等[39]提出一种基于特征相关和特征归一化的网络流量分类的快速预处理方法。此方法基于特征直方图的归一化，特征直方图即为用直方图的形式来表示特征的划分。具体实现方式如下。

滑动窗口的每个特征fi被划分为b1,b2,…,bm，m=n1/2+1，n为特征的数量，b1=[min,k1)，b2=[k1,k2)，bm=[km-1,max]（其中k表示阈值，k=(maxi-mini)/m)。每一个区间称为bin，bk表示落在第k个bin中样本的数量，每个bin的高度为样本落在此区间的相对频率fri，其中fri=fqj/N（其中N为样本总数，fqj表示为样本落在binj的数量）。样本直方图如图10所示。

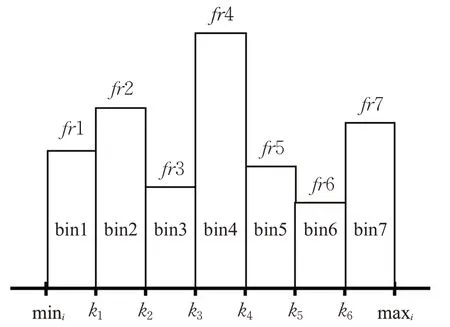
图10 特征直方图划分Fig.10 Feature histogram division

对于每一个滑动窗口，首先获取到每个特征的最小值和最大值，在生成单个滑动窗口的样本直方图之后再通过滑动窗口获取新的最大、最小值。如果新的滑动窗口的最小值小于前一个滑动窗口的最小值或者新的滑动窗口的最大值大于前一个滑动窗口的最大值，即mini-1＜mini或maxi-1＞maxi，则创建新的仓，直至区间包含新的最小值或最大值再停止建仓。划分好所有的仓之后，即特征直方图建立完毕，再将所有的仓近似为正态分布则完成归一化操作。与此同时，在建立新的仓的过程中，由于是动态建立，可以实时观察到异常点的出现。

优点：可以实现流数据归一化并检测异常点。

缺点：计算效率不高，在无限数据的情况下，不适合在内存中存放。

2.2.3 窗口平均值变化百分比

为解决不断变化的大数据流规范化问题，Gupta等[40]提出了一种分布式的大数据流自适应规范化的方法。此方法提供了一个简单的机制，以适应每个窗口中不断变化的数据的规范化统计。

主要方法如下：

第一步：获取第一个窗口的统计数据（比如最大值、最小值、平均值等），将这些数据设置为初始的参考数据。第一个窗口使用这些参考数据进行Min-Max归一化。

第二步：滑动到下一个窗口后，计算当前窗口和上一个窗口之间平均值的百分比变化，用于检测是否有重大变化。自行定义一个阈值，如果百分比的变化超过阈值，当前窗口的最大最小值将取代原始的最大最小值作为新的参考值；反之，当百分比变化不超过阈值时，数据流变化被看成是不重要的，为保持最大最小的实际范围并消除对一个窗口的依赖，参考的最大最小值将被逐步更新，选取两个窗口更小或者更大的那个值作为新的参考值。

优点：可以应用于全领域的数据流。

缺点：阈值无法动态调整。

2.2.4 动态调节窗口大小

Gupta等[41]提出了一种基于自适应窗口大小的规范化方法，主要方法是根据数据速率来调整窗口大小。如果数据速率增加，则窗口大小减少；反之，如果数据速率减少，则窗口大小增加，以保证在一个理想的速率中处理数据，方法流程如下。

第一步：首先将第一个窗口作为当前窗口，使用当前窗口的最大最小值，对其进行Min-Max归一化。

第二步：当下一个窗口到来时，将这个窗口代替前一个窗口作为当前窗口，比较当前窗口和前一个窗口的数据率，预测下一个窗口的大小或时间间隔。数据率百分比计算如下：rw=rc/rp（其中rc表示当前窗口的数据速率，rp表示前一个窗口的数据速率）。自行定义一个理想数据率r来作为阈值。比较rw和r的大小，如果rw小于r，则将窗口长度增加一个固定的常数c，反之，如果rw大于r，则将窗口长度减少一个固定的常数c，其中c自行定义。

第三步：改成理想速率的窗口大小后，用修改后的窗口里的最大值和最小值来对窗口中的数据进行Min-Max归一化。

优点：能保持一个稳定的数据处理速度。

缺点：暂时没有实验来证明。

2.2.5 时间序列归一化

对于时间序列数据来说，时序性是其重要特征[42]。由于时序数据具有高维度、动态性等特点，直接对时序数据进行分析会无法提取有用信息，甚至得出错误结果。对时序数据进行预处理也是时序数据分析的重要步骤[43]。在非稳定的时间序列流的归一化方面，Passalis等[44]提出一种进入深度神经网络前的深度自适应归一化层，Ogasawara等[45]提出了一种对非平稳异方差（具有非均匀波动性）时间序列进行归一化的新方法。该方法被命名为自适应归一化（AN）。其完整的数据归一化过程可分为三个阶段：（1）将非稳态时间序列转化为稳态序列，从而创建一个不相交的滑动窗口序列（不重叠）；（2）去除离群点；（3）数据标准化。

具体步骤如下：

第一步：基于移动平均数，将非平稳的时间序列转换成一个平稳的时间序列。先计算原始时间序列的移动平均数，使用其值来创建一个新的静止序列，并将这个序列划分成不相干的滑动窗口。

第二步：利用箱型图来检测数据的异常值，检测出来的异常值根据情况进行调整。

第三步：对做过处理后的数据使用这个序列的全局统计信息（最大值、最小值等）进行Min-Max归一化。

优点：每个相对的滑动窗口内保留原有的时间序列属性。

缺点：暂无。

2.2.6 SUCR-DTW

在动态时间扭曲下时间序列的相似性搜索上，归一化操作极有必要，Giao等[46]提出SUCR-DTW方法，包含增量化的归一化法。主要方法如下：首先，用Quic-ksort算法从数据点创建一个升序数字数组，先对时间序列的子序列排序，然后插入新数据移除老数据，最后Min-Max归一化。由于是时间序列归一化的同时进行相似性搜索，相似性搜索过程中需要更新首尾的最大最小值，使用Quicksort对其进行排序，xmin是排序数组的第一个元素，xmax是最后一个。在删除和插入的过程中必须保持数组的升序，所以还需要使用二进制搜索的算法来寻找需要删除的元素和插入新数据点的合适位置。

2.2.7 NSPRING

在时间序列匹配上，Sakurai等[47]提出动态时间扭曲（dynamic time warping，DTW）距离下的子序列匹配方法SPRING，SPRING不支持归一化，而归一化在匹配中极为重要。Gong等[48]提出基于SPRING的归一化方法NSPRING。该方法选取一个暂时性的子序列S′用于存储原序列S，但S′的长度等于查询序列Q，当一个新的时间节点进入，最开始进入的时间节点就会被删除，维持S′的长度等于查询序列Q的长度。随着S′不断更新，当S′的长度等于查询序列Q时，NSPRING算法开始，存储序列S′可以被用于计算整个时间序列的均值和方差，继而对整个时间序列S进行Z-Score标准化运算，从而实现时间序列的归一化。

表3列出多类流数据归一化算法，从窗口及评判标准两个维度进行对比。窗口细化分为固定窗口和滑动窗口，评判标准细化为4个评判标准，用于评判是否进行归一化操作或者是否更新归一化参数。

表3 流数据归一化算法对比Table 3 Comparison of stream data normalization algorithms

3 总结与展望

数据归一化是数据预处理的重要一步。无论是在深度学习还是时间相似性搜索等方面都起了极大的作用。本文收集并整理了归一化方法相关文献，从数据类型角度对这些归一化方法进行划分，凝炼提出了基于流数据的归一化分类方法。将数据归一化方法划分为基于批数据的归一化法和基于流式数据的归一化法。本文首先对归一化的研究现状以及发展趋势进行了详细分析，通过收集相关文献，以数据类型作为切入点，提出了基于流式数据的归一化分类方法。然后，将批数据及流数据归一化方法从学习模式与处理阶段两个维度进行梳理。在大数据流的场景下，对于窗口和输入数据归一化方法的选择也至关重要。在不同的场景下，使用特定的方法可以更有效地防止神经网络因数据量纲的复杂性而错误建模并提高预测正确率等。由于流式数据的应用需求日趋急迫，对流式数据的研究也逐渐成为各领域的重点。基于流数据的归一化面临着一些亟待解决的问题。

（1）海量样本下归一化算法的鲁棒性。随着大数据技术的发展，呈现出海量、复杂的数据特点。在海量数据的应用中，常常会出现异常值，而归一化可能会受到异常值的影响。因此，如何在流式场景下，面对海量样本的情况下，保证数据的鲁棒性是当前需要解决的问题。

（2）自适应性。不同的流式数据应用需要与此最适合的归一化方法，手动选择并调整归一化方法会消耗大量人力物力资源。到目前为止，并没有一个通用的自适应方法以供选择。

总体来说，由于流式数据应用必须在时间和资源的严格限制下处理数据，这为流数据应用带来了极大的挑战。流式数据场景下的归一化研究相对缺乏，在流场景下的归一化方法还有许多需要研究的方向。

（1）面向深度网络的动态自适应归一化法。当前深度神经网络的应用作用于各行各业，并取得了显著的效果。但对于深度学习的归一化研究大多停留在隐藏层的归一化方法，对于流式数据在输入层的归一化方法则相对缺乏。当前仅有的基于流式数据的归一化方法需要手动调整，缺乏一个通用的归一化方案。将来关于归一化的研究应该致力于如何避免消耗大量人力资源下对流数据进行自适应的动态归一化操作。在深度神经网络中使用这样的方法是当前的一个重要研究方向。

（2）大数据流下归一化法。数据的大规模增长是当前大数据分析的一个主要问题。由于大数据呈现出海量、复杂的数据特点，在数据挖掘等应用下，对大数据应该进行归一化的预处理，以实现应用更好的性能与精度。而大数据流处理方法对时间和资源有着严格的限制，这对流式场景下的归一化研究具有重大挑战。因此，如何在大数据流场景下，设计一种更具适应性归一化方法具有重要的理论意义与实用价值。