基于EMD-LSTM预测模型与夏普比率风险回溯的交易策略研究

佟 磊，张 媛，吉宇豪，吴思青

(1.东北大学 工商管理学院，辽宁 沈阳 110819；2.首都经济贸易大学 财政税务学院，北京 100070)

1 引言

在现有针对时间序列的预测模型的研究中，牛红丽等[1]提出用GRU模型预测股票价格指数；朱俊蓉等[2]根据ARIMAX模型，基于人民币汇率的时间序列进行预测；黄玉成等采用LSTM模型，基于以往股票价格这一时间序列进行预测。基于以上研究内容，结合学者的研究和现实情况，将预测模型相互比较，提出一种基于EMD-LSTM预测模型与夏普比率风险回溯的交易策略。

2 数据说明

文章主要考虑交易者同时持仓黄金和比特币两种交易物时的情况，数据分别取自2016年9月11日至2021年9月10日黄金与比特币市场五年交易期内各交易日的交易物收盘价，即一盎司黄金的美元收盘价与指定日期单个比特币的美元价格。

3 基本假设

(1)只进行做多操作，不考虑做空的情况；

(2)在每日临近收盘时执行交易；

(3)认为数据中的每日价格均为收盘价格。

4 预测模型

4.1 数据滚动窗口的建立

为了能滚动地训练、测试、预测基于价格的时间序列，设置一个数据滚动窗口，将时间序列预测问题转化为经典的监督学习问题。令滞后特征为7(lag_days = 7)，即在训练集中，每日使用前7日的数据进行训练得到训练集的标签，在测试集中，每日使用前7日的数据进行训练得到最新的预测数据，往复进行，动态地不断生成固定数量的训练集和测试集。

4.2 EMD

经验模态分解(EMD)是由Huang等[3]提出的自适应信号时频处理方法。EMD从非线性、非平稳的对数收益率时间序列中根据数据本身基于时间尺度的信号进行分解，分解出有限个组内禀模态函数(IMF)，分解步骤如下：

(1) 找出时间序列中所有的极大值和极小值；

(2) 用三次样条插值函数将所有极值点拟合到上包络U(t)和下包络L(t)上；

(3) 计算上下包络线的局部平均值m(t):

(4) 从S(t)中减去m(t)，得到新的时间序列h(t)。

h(t)=x(t)-m(t)

(5) 用h(t)作为新的输入序列重复步骤 (1)～(4) ,直到h(t)的平均值接近零，此时得到第一个模态函数IMF，记为Ci(t) (i=1,2,3，…，N)。

(6) 将Ci(t)从原始序列S(t)中分离出来，得到一个没有高频分量的差分序列:

(7) 以ri(t)作为新的输入序列重复步骤(1)～(6),直到满足终止条件(通常使得最后的余数满足单调性)。

通过上文中得到的记录为Ci(t)的诸多IMF，可将S(t)分解结果表示为：

4.3 EMD的应用

在本模型中，黄金和比特币的交易市场与金融市场类似，其价格变动是一个非线性、非平稳的复杂动态系统。在将金融时间序列输入深度学习框架之前，笔者需要对数据进行预处理。首先处理原始对数收益率的时间序列S(t)。

计算某一日的对数收益率r，将对数收益率作为自变量输入到EMD中：

ri=ln(pi)-ln(pi-1)

使用Python编写EMD程序，可得到比特币和黄金的数个模态函数IMF。见图1。

图1 EMD处理黄金数据结果

4.4 LSTM

LSTM是深度递归神经网络的代表，尤其擅长处理序列数据。其引入了门控制单元系统，使用不同的“门”来让网络学习。

LSTM的门结构：

其中，激活函数σ是在0和1之间具有值的Sigmoid函数，bf、Uf、Wf分别是偏差、输入权重和遗忘门的递归权重。

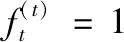
其中，b、U、W表示偏差、输入权重和LSTM单元中递归权重。

其中，激活函数σ是sigmoid函数，x(t)是当前的输入向量，h(t)是当前的隐含层向量，bg、Ug、Wg分别表示输入门偏差、输入权重和递归权重。

其中，b0、U0、W0分别表示偏置、输入权重和输出门递归权重。

得益于三个控制门和存储单元，LSTM能容易地保持、读取、复位和更新长时间信息。另外，由于LSTM内部参数的共享机制，可以通过设置权重矩阵的维度来控制输出的维度。LSTM 在输入和反馈之间建立了一个长时间的延迟。梯度既不会爆炸也不会消失，因为存储单元的内部状态保持着连续的误差流[4]。

4.5 Emd-LSTM

EMD处理时间序列后，用Python编写LSTM程序以滞后特征=7的数据滚动窗口动态往复地训练和预测，得到以下预测结果。详见图2、图3和表1。

图2 EMD-LSTM对比特币价值拟合效果

图3 EMD-LSTM对黄金价值拟合效果

表1 拟合曲线方差

可以看到，预测价格曲线与实际价格曲线高度拟合，EMD-LSTM模型预测效果极佳。

5 基于夏普比率风险回溯的交易策略

5.1 策略开发

首要计算预期收益率。

由以上的预测模型，在每日临近收盘时给出明日的预测值，并决定交易。此后，设定一个交易阈值τ，经过交叉验证调试，发现阈值设置为比特币τB=8%、黄金τB=0.7%时表现较为优异，收益较高。设黄金的交易费用率αG=2%，比特币的交易费用率αB=1%。

操作策略为：

式中，“h”表示不操作，“1”表示此种交易物满仓，“0”表示此种交易物空仓。

第一年时，因为缺乏往年数据，保险起见将比特币和黄金平均分仓为500元/仓分别进行决策，即比特币和黄金的仓位均为500元。从第二年起(即从2016年10月25日/2016年10月26日+360日后的第一天)，根据前一年的实际数据计算出交易物的夏普比率Sp：

式中，E(RP)表示交易物的平均收益率，Rf表示无风险收益率，取2%，σp表示收益率的标准差，即每一个风险能带来多少收益。

下一年的分配为：

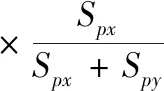
5.2 策略模拟

假设初始资金为1000美元。

在由EMD-LSTM得到t+1日的价格预测值后，计算预期收益率后在第t日临近收盘时决定交易策略。在第一年内，比特币和黄金的资金分配均为500元。且在前几个交易日内，因训练数据较少，模型预测效果偏差较大，保守起见均保持观望，即持有现金(比特币为前80个交易日，黄金为前50个交易日)。

从第二年起，根据以往年份交易物的实际价格计算出夏普比率Sp(见表2)。

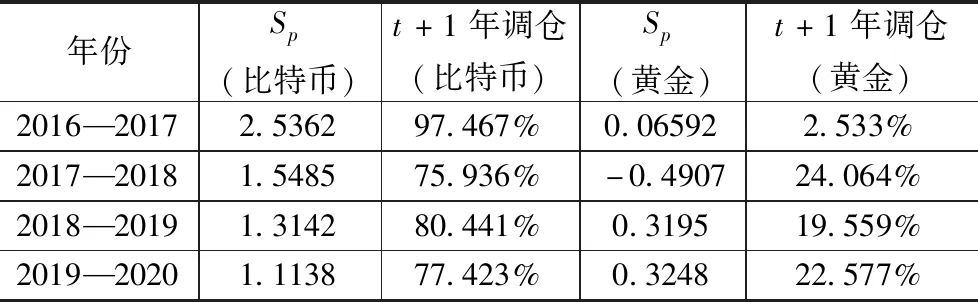
表2 各年夏普比率

最终，2016年9月11日价值1000美元的投资款在2021年9月10日得到黄金和比特币的资产分别为116104.26美元和5970.25美元，总资产为122074.52美元。

5.3 交易策略对比

图4表示选取比特币在初始投资一单位资金的情况下，使用策略进行操作与持仓不进行操作的单位净值变动情况。

图4 EMD-LSTM比特币策略对比

可以看到，操作比特币使用策略的收益远高于不进行操作，使用操作策略是较优且必要的。

5.4 预测模型对比

相比于EMD-GUR、RNN、ARIMAX、LSTM预测模型的策略，基于EMD-SLTM预测模型的策略在对预测价格的拟合准确度上有显著优势。LSTM黄金价格拟合曲线见图5。

图5 LSTM黄金价格拟合曲线

分别计算黄金和比特币的以下拟合指标：MAE(平均绝对误差)、MAPE(平均绝对百分比误差)、MSE(均方误差)、RMSE(均方根误差)、NMSE(归一化后均方误差)。黄金五模型方差比较见表3。

表3 黄金五模型方差比较

经过拟合五方差指标分析，在所比较的EMD-LSTM、EMD-GRU、ARIMAX、LSTM、RNN五个模型之间，EMD-LSTM在预测价格上有着最优异的拟合精度，各模型拟合关系不等式为EMD-LSTM >EMD-GRU >ARIMAX >LSTM >RNN。

此外，分别使用五个模型以相同的交易策略运行，由表4可以明显看出，使用EMD-LSTM模型进行交易能获得最高的收益(122074.52美元的净资产)，且区间绝对收益、年化收益也均高于其他四类模型，收益关系不等式为：EMD-LSTM >ARIMAX >EMD-GRU >RNN >LSTM。各模型总资产比较见图6。

表4 五个模型以相同的交易策略进行的收益

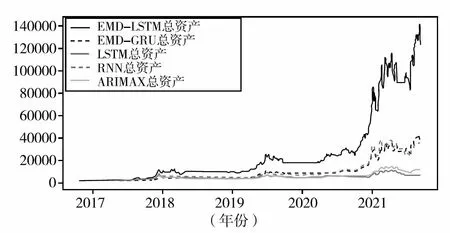
图6 各模型总资产比较