基于三维重构的钢桥表面锈蚀提取方法研究

倪有豪，王 浩，茅建校，贡照华，惠 卓

(1.东南大学 混凝土及预应力混凝土结构教育部重点实验室，江苏 南京 211189；2.中国铁路上海局集团有限公司 南京桥工段，江苏 南京 210011)

随着现役钢结构桥梁运营年限不断增长，日益累积的病害对其日常养护管理工作带来新的挑战，同时对养护技术、质量、效率提出新的要求[1-2]。表面锈蚀作为钢结构桥梁最常见的病害之一，其检测方法的可靠性与及时性能有效降低工程事故的发生概率，延长桥梁结构的服役寿命[3]。目前，应用图像处理技术已实现基于二维图片的钢桥表面锈蚀提取。如，Son等[4]提出基于颜色空间、支持向量机、决策树、K近邻等分类处理手段的钢桥表面锈蚀提取方法；Yi等[5]采用卷积神经网络模型识别钢材表面锈蚀区域；王达磊等[6]通过对锈蚀图像进行语义分割，实现钢桥表面锈蚀区域的检测与定量分析。然而，基于图像处理的锈蚀提取方法难以实现钢桥表面锈蚀的三维提取和可视化。

近年来，三维点云技术的飞速发展为实现病害三维的提取及可视化提供了可能，且在旧桥病害重构、变形监测等方面取得卓有成效的研究成果。文献[7-8]基于无人机倾斜摄影分别对砌体拱桥和混凝土桥进行三维重构，为旧桥病害分布及严重程度分级提供依据。Ye等[9]以点云格式记录桥梁几何形状，通过分割成不同结构单元与拟合原始形状比对，实现旧桥变形和位移长期监测。Armesto等[10]提出一种依据沿拱顶截面对称性准则确定拱顶变形的方法，实现无任何经验参数情况下拱桥历史变形的准确获取。熊文等[11]通过对构件点云模型的时空变化趋势进行跟踪，进行桥梁结构力学现状的判断及发展趋势的预测。然而，基于三维点云在钢结构桥梁锈蚀方面的提取方法研究却鲜有公开文献报道。

为实现钢桥表面锈蚀的准确提取及可视化，本文将点云在桥梁病害方面的研究拓展至锈蚀提取方面。在掌握钢结构锈蚀颜色分布特征规律的先验知识基础上，结合K-means聚类算法和最大类间方差法获取钢桥锈蚀最佳分割阈值，并运用三维点云模型实现桥梁表面锈蚀的可视化，形成一套钢结构桥梁表面锈蚀准确提取方法，用该方法识别某钢桁拱桥表面的锈蚀区域，运用视觉分析和定量分析对提取的锈蚀区域进行精确评价，并验证方法的有效性。

1 基于三维点云和聚类算法的钢桥表面锈蚀提取方法

1.1 基于倾斜摄影的钢桥点云模型

点云模型是基于倾斜摄影原理从多角度获取影像数据匹配生成的三维模型，更加客观地反映物体的三维信息[12-13]。对生成的钢桥点云模型进行滤波，剔除无效数据，如错误数据、噪声、孤立点等。对点云模型中存在的大尺度噪声，一般表现为孤立点，即与主体模型偏离较远，可采用基于空间分布的去噪(Statistical Outlier Removal，SOR[14])算法进行粗差剔除。进行粗差剔除后的点云模型，根据需要选择滤波器对噪声进行滤除。均值滤波、中值滤波、高斯滤波都是典型的滤波方法[15]。其中均值滤波采用邻域模板像素的均值代替目标像素的方法实现滤波；中值滤波可消除椒盐噪声；高斯滤波采用卷积形式实现滤波，适用于符合正态分布规律的噪声。

1.2 锈蚀提取相关方法 1.2.1 K-means聚类算法

传统K-means聚类算法是从原始数据集中随机选取K个数据点进行聚合，作为初始聚类中心[16]。在给定D维欧几里得空间的原始数据集(x1,…,xN)，将该组数据聚成K个簇。

引入二值变量rnk∈{0,1}(n=1,…,N;k=1,…,K)来表示数据xn对聚类K的归属，定义损失函数J为

(1)

式中：uk为聚类中心。目标是寻找使损失函数J最小的所有数据点的归属集{rnk}和聚类集{uk}。

1.2.2 最大类间方差法

最大类间方差法是日本学者大津提出用于图像自适应的一种阈值分割算法[17]，该算法通过图像的灰度特征确定分割阈值，使目标和背景的类间方差取最大值。

假设点云模型中背景部分与锈蚀部分的分割阈值为k0，则类间方差σ2表达式为

σ2=ρ1(μ1-μ)2+ρ2(μ2-μ)2=

ρ1ρ2(μ1-μ2)2

(2)

s.t.ρ1+ρ2=1

(3)

ρ1μ1+ρ2μ2=μ

(4)

式中：μ1为背景部分点平均灰度值；ρ1为占整个点云模型的比例；μ2为锈蚀部分点平均灰度值；ρ2为占整个点云模型的比例；μ为整个点云模型点的平均灰度值。

当类间方差取值越大，说明锈蚀部分与背景部分的差别越大，因此当σ2取极大值时所对应的阈值k0为最大类间方差法确定的分割阈值。

1.3 技术路线

基于三维点云和聚类算法的表面锈蚀提取技术流程见图1。该方法主要步骤如下：

Step1采用无人机搭载高清相机的方式对钢结构桥梁进行拍摄，利用倾斜摄影原理形成钢结构桥梁的三维点云模型。

Step2对点云模型进行预处理，即运用SOR滤波进行粗差剔除以及选取合适的滤波器进行滤波去噪等。

Step3统计点云模型中的RGB颜色三通道灰度分布直方图，利用样本K-S检验其三通道灰度分布特征，得到双峰均值作为K-means聚类算法的初始聚类中心。

Step4对K-means聚类算法不断迭代得到中间分割阈值，结合最大类间方差法得到阈值，获取最佳分割阈值。

Step5将锈蚀从点云模型中分割出来，通过CloudCompare软件进行锈蚀分布可视化。

2 工程应用

2.1 工程背景

某大桥是京沪高速铁路一个重要的组成部分，自投入运营以来，已走过近十年风雨。钢桁桥主体结构整体涂装为蓝色[18]。根据锈蚀形状特点，已出现点状、斑状、整体均匀锈蚀。依据高铁桥梁10 a一次大检查的标准，目前需对大桥进行健康检查，包括涂装层表观锈蚀检查。本研究采用大疆M300RTK无人机，搭载WP-E2单云台相机，拍摄分辨率达到6 K。

2.2 点云模型预处理

基于无人机获取的钢桥倾斜照片，形成全桥三维点模型，见图2。图2中展示背景均选为灰色。由于全桥点云模型所含点云数量巨大，对计算机处理性能有极高要求，因此从中选取4个构件点云模型，即2个钢桁架节点、1个弦杆、1个桁架小车，进一步进行预处理及锈蚀提取。实验环境为Matlab 2019a、Agisoft PhotoScan、CloudCompare。

图2 钢桥三维点模型

2.3 基于RGB颜色空间的锈蚀分布特征

朱言江等[19]提出一种基于双峰法的遥感图像分割中阈值确定方法，图像的前景与背景在灰度直方图上形成双峰，最低谷处为分割阈值，在前景和背景对比较强时分割效果较好。涂装颜色非红色的钢结构桥梁可将锈蚀部分作为前景，而非锈蚀涂装部分作为背景进行阈值分割，满足双峰统计特性。

钢桥点云模型锈蚀部分颜色空间分布见图3。将锈蚀部分进行RGB三通道灰度值皮尔逊相关性分析可得：R、G色灰度值皮尔逊相关性系数为0.713，G、B色灰度值皮尔逊相关性系数为0.785，R、B色灰度值皮尔逊相关性系数为0.227。由此可知，G色灰度值与R、B色相关性大，而R、B色相关性小。故本文分割阈值计算方面，忽略G色分量，仅考虑R、B色分量。

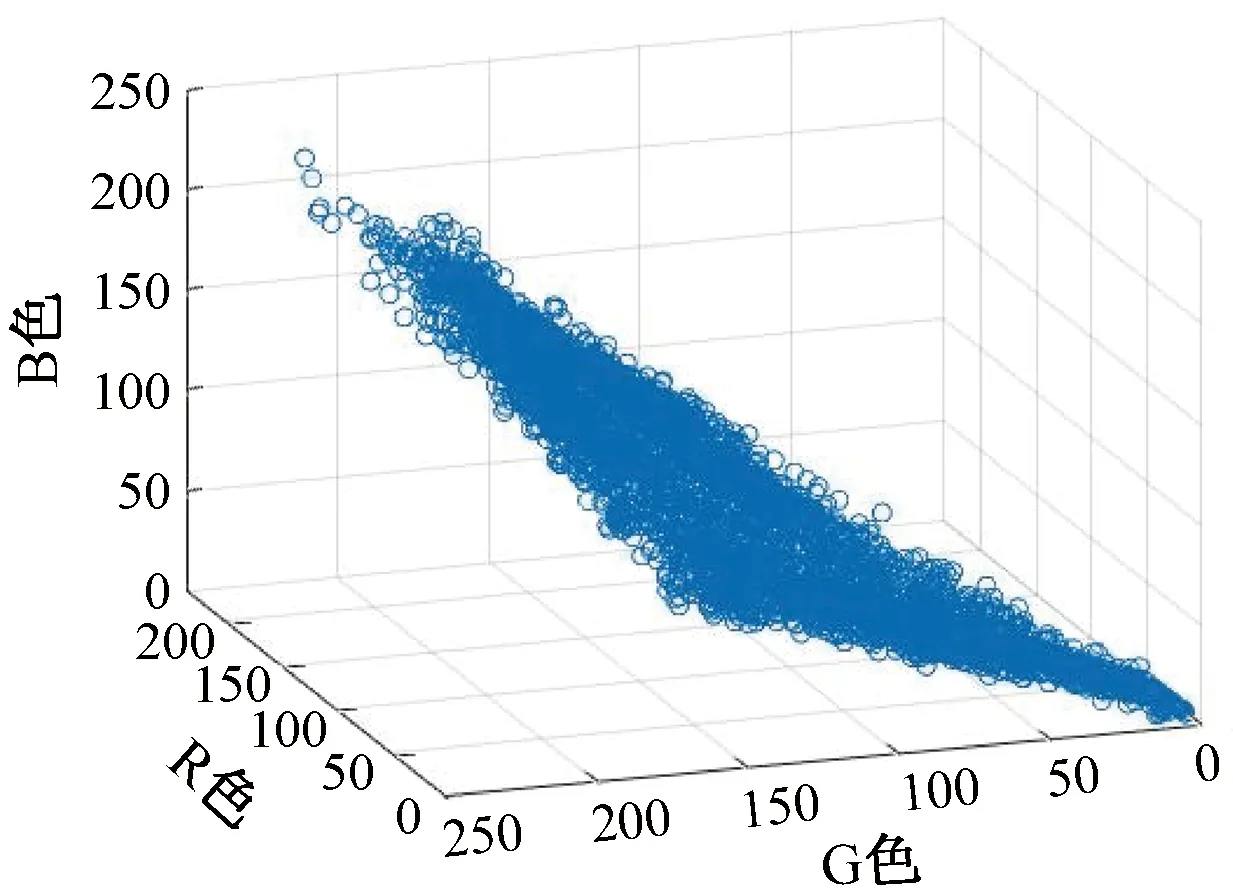
图3 钢桥点云模型锈蚀部分颜色空间分布

钢桥点云模型颜色空间灰度分布直方图见图4。由图3、图4可知，R色的灰度值明显偏向靠近255级一侧分布，B色的灰度值明显偏向靠近0级一侧分布，呈现双峰现象。

由图4(a)、图4(c)可知，靠近灰度值为0级的左峰，正态分布检验不明显，但为研究方便近似认为其服从正态分布。这个假设不影响K-means最终聚类中心的数值，原因为：①在R色灰度分布直方图中，对右侧正态分布直方图进行概率密度函数曲线拟合，取95%置信区间下限作为R色分割阈值；②在B色灰度分布直方图中，对右侧正态分布直方图进行概率密度函数曲线拟合，取95%置信区间下限作为B色分割阈值；③求得双峰的两类均值作为K-means聚类算法的两个初始聚类中心。

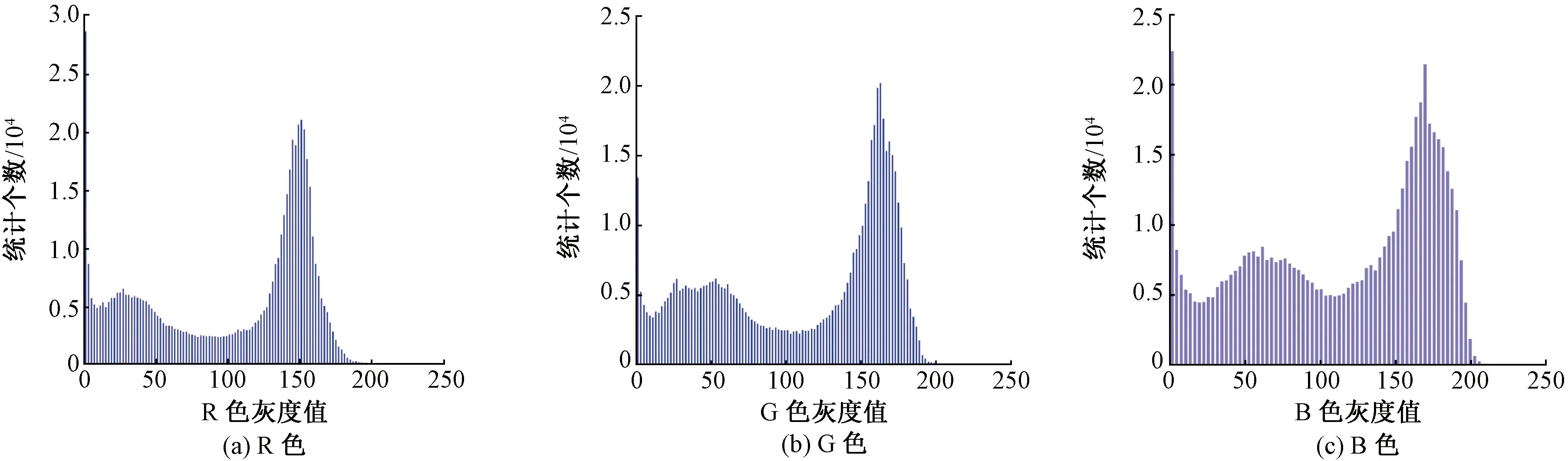
图4 钢桥点云模型颜色空间灰度分布直方图

对灰度值靠近255级的右峰进行样本数据正态分布P-P图检验，见图5。由图5可知，累积概率散点在直线附近轻微波动，认为样本数据基本服从正态分布。对右峰进行正态分布K-S检验，精确显著性水平为0.048，略小于0.050，认为基本服从正态分布。

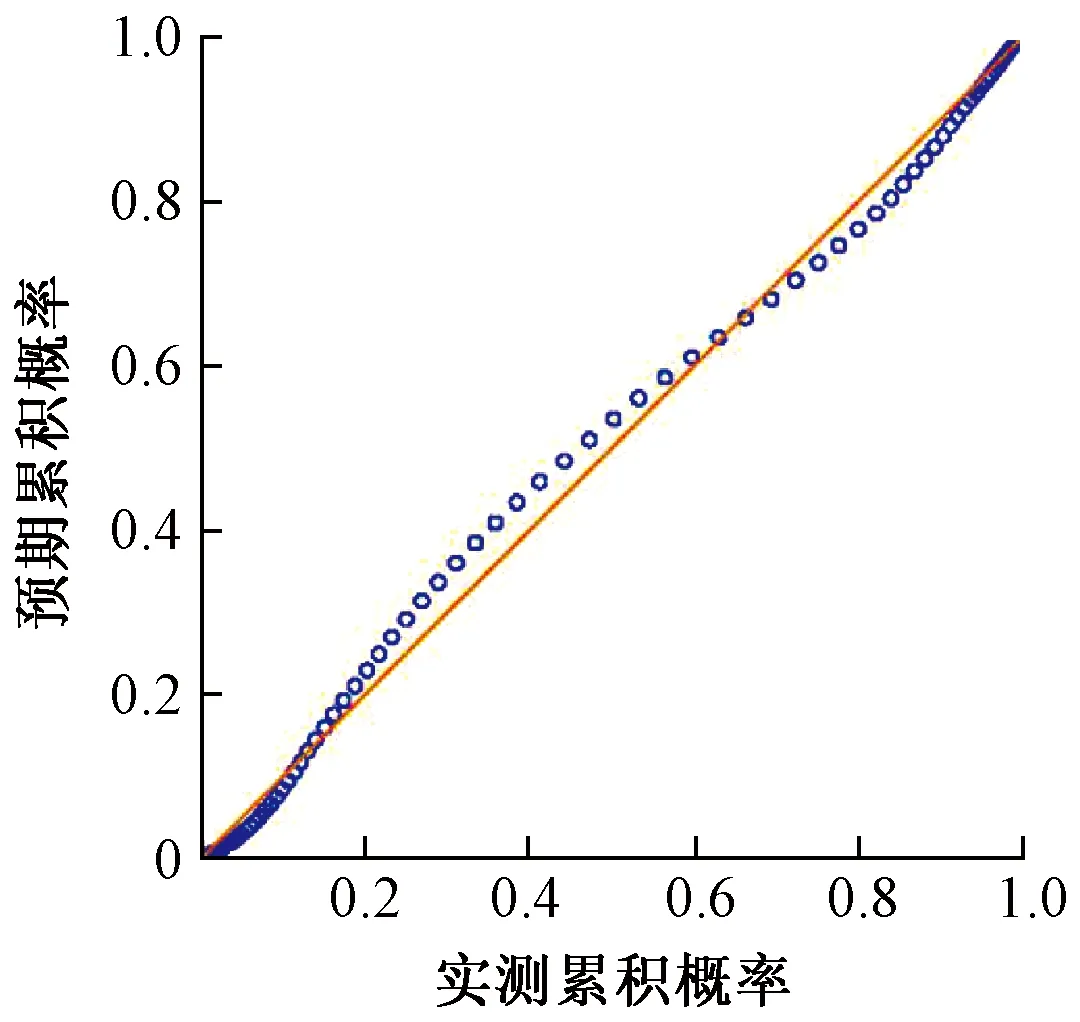
图5 正态分布P-P图

2.4 最佳分割阈值确定

点云模型锈蚀的最佳分割阈值确定方法，具体步骤如下：

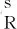
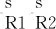
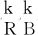
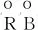
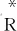
(5)

根据式(5)，将点云模型中的锈蚀部分从背景部分分割出来，并结合点云处理软件CloudCompare，将锈蚀部分在钢桥中可视化展示。

3 锈蚀识别结果分析

采用两种评价方法对钢桥表面锈蚀提取进行精准度评估：①视觉分析；②定量分析。

3.1 视觉分析和定量分析

将提取出来的锈蚀点云模型与原点云模型进行三维配准，通过目视对比方式分析锈蚀提取的精度。点云模型锈蚀提取结果见表1。为提高视觉效果，将锈蚀点云模型用彩色云图进行表示，蓝色为锈蚀程度较轻，绿色为锈蚀程度中等，红色为锈蚀程度较重。由表1可知，提取的锈蚀点云与滤波后点云模型的锈蚀区域吻合度高。

表1 点云模型锈蚀提取结果

钢结构锈蚀是面状目标，点云模型是物体表面点的信息集成。将提取锈蚀的点数量与点云模型的点数量作为定量评价参数，正确提取率R、漏提取率M、误提取率W表达式分别为

R=n1/n×100%

(6)

M=n2/n×100%

(7)

W=n3/n×100%

(8)

式中：n为目标构件的锈蚀总点数量；n1为目标构件中被识别出来的正确锈蚀点云数量；n2为目标锈蚀区域中未被识别出来的正确锈蚀点云数量；n3为目标构件中被误识别为锈蚀的点云数量。

通过CloudCompare软件对提取出的锈蚀点云模型点数量进行统计，统计结果见表2。由表2可知，平均正确提取率达到90.1%，漏提取率、误提取率分别为9.9%、8.2%。造成钢桁架节点、弦杆、腹杆的锈蚀区域正确提取率差异较大的原因是光照的明暗度对颜色灰度值的影响。

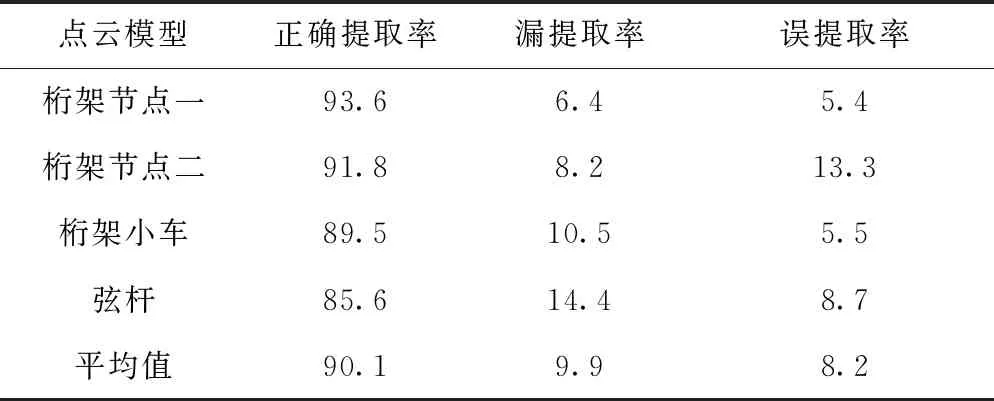
表2 锈蚀提取精准度 %

3.2 锈蚀提取结果

4个点云模型的总数量为24～194万个，大跨桥梁整桥点云模型的总数量达到千亿级别。将提取锈蚀点数与构件点云的点数之比作为构件的计算锈蚀率，对构件锈蚀状态进行评估。

钢桥构件的锈蚀提取结果见表3。由表3可知，桁架节点二的锈蚀率最低为1.3%，而弦杆的锈蚀率最高为9.4%。依据CECS343—2013《钢结构防腐蚀涂装技术规程》[20]对重新涂装前的钢结构表面锈蚀程度的规定，本文构件的锈蚀等级为3～4级，需对构件重新喷漆涂刷的面积达到18%～40%。

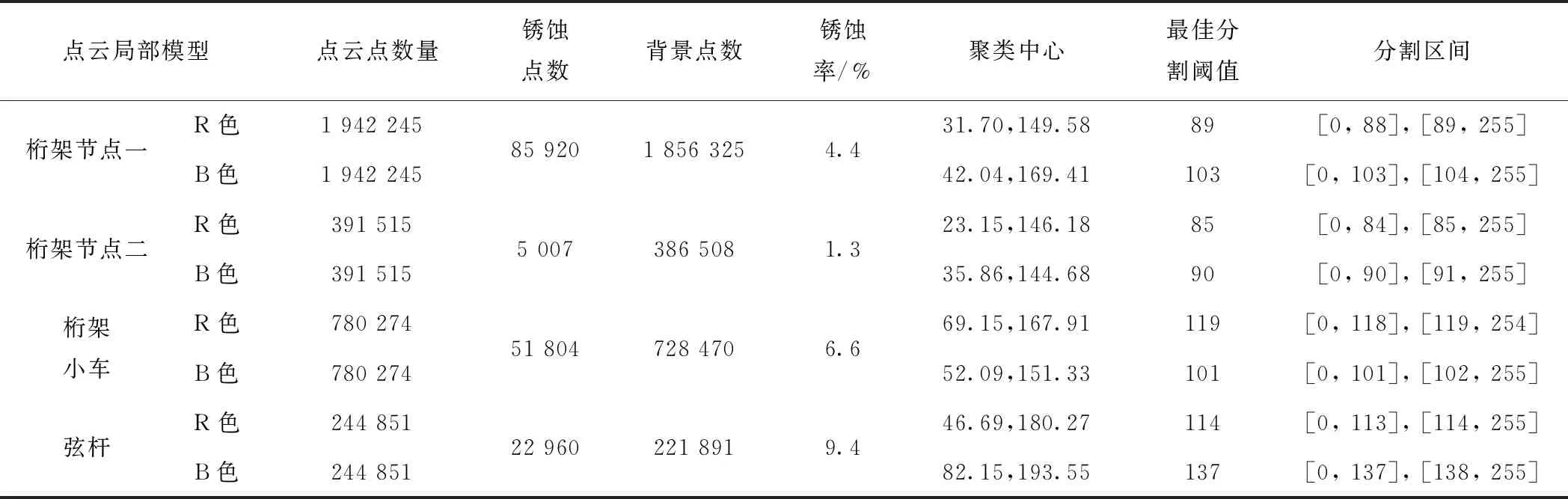
表3 钢桥构件的锈蚀提取结果

3.3 与图像处理方法比较

采用K-means聚类算法、最大类间方差法分别对钢桥的4个节点图像进行锈蚀识别，并对识别结果进行比较，结果见表4。

由表4可知，最大类间方差法难以准确提取钢桥节点图片中的锈蚀区域。运用K-means聚类算法对图像进行聚类分析，其锈蚀提取效果受K值影响较大，当K较小或K较大时，图像聚类的效果较差，均难以提取锈蚀区域。如对弦杆节点进行锈蚀提取时，由于弦杆节点图像包括背景色、浅蓝涂装色、深蓝涂装色、锈蚀色4类颜色，当K=4时，能较好地识别出节点的锈蚀区域。

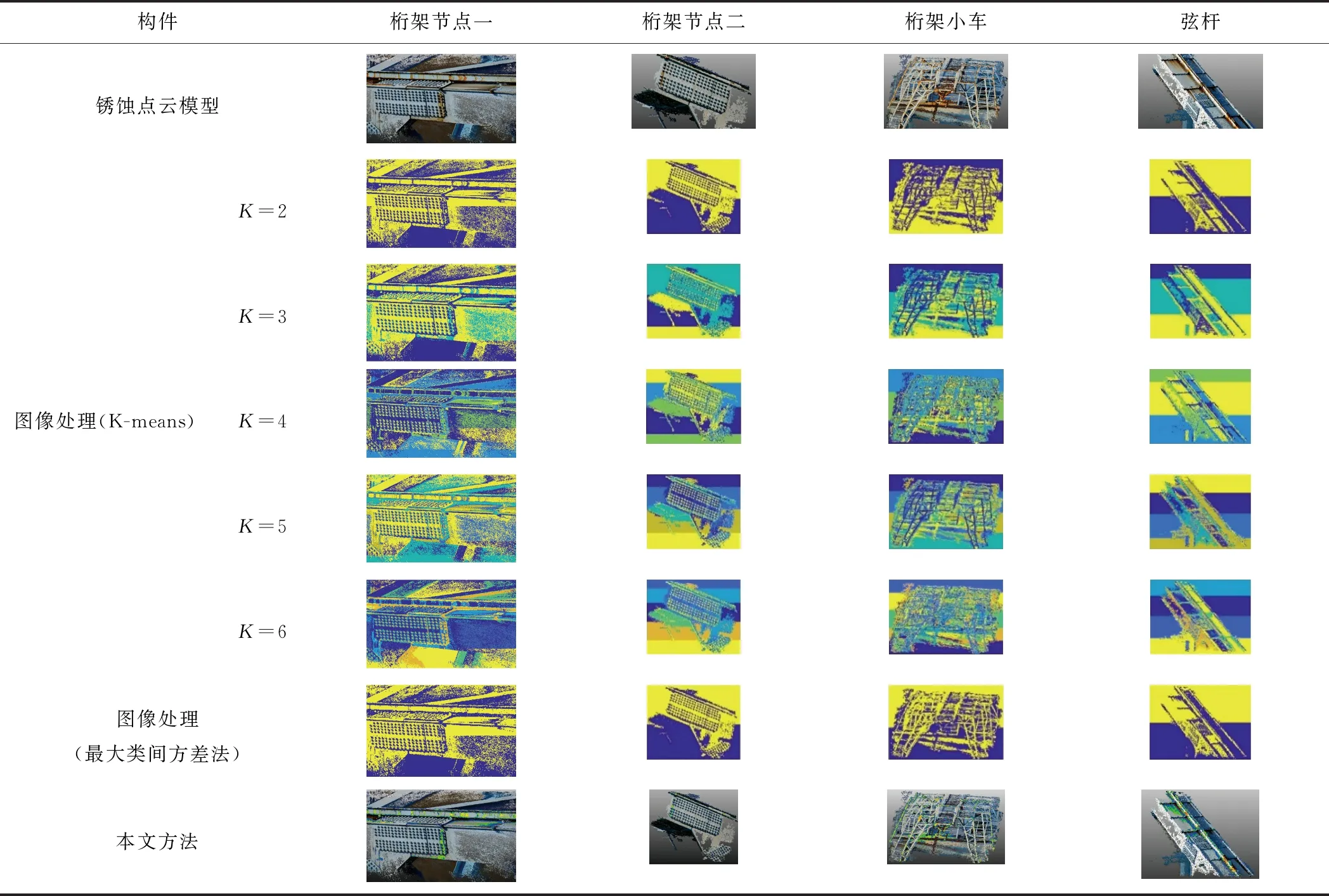
表4 本文方法与图像处理方法的比较

与基于K-means聚类算法的图像锈蚀提取方法相比，本文提出的方法能更精确地提取出钢桥节点的锈蚀区域，锈蚀的平均正确提取率可达90.1%。其原因为本文方法基于三维重构模型，可在空间上将环境背景与桥梁分离，同时考虑RGB颜色空间的统计规律。而图像聚类方法将R、G、B三通道颜色转化为单值灰度图像进行单通道聚类，忽略了RGB颜色空间的灰度统计规律。

4 结论

本文提出一种钢结构桥梁表面锈蚀准确的提取方法，并结合点云模型实现锈蚀分布的可视化，基于某钢桁拱桥的锈蚀区域的识别与精确评价，验证了该方法的有效性。研究结论如下：

(1)结合数理统计方法、K-means聚类算法、最大类间方差法，有效地确定锈蚀点云模型中RGB颜色通道的最佳分割阈值，实现钢结构桥梁表面锈蚀的准确提取。

(2)基于倾斜摄影原理形成的三维点云模型中，桥体与环境背景分割开，克服二维图像处理方法中难以剔除环境背景的缺点。

(3)基于点云模型给出构件计算锈蚀率方法，对构件锈蚀程度进行评估，并实现锈蚀分布的可视化，为钢结构桥梁运维管养提供参考价值。