基于系统韧性理论的城市轨道交通信号系统设计

高 翔 张凌翔

(1.上海电气泰雷兹交通自动化系统有限公司，201206，上海;2.上海申通地铁集团有限公司，201103，上海∥第一作者，高级工程师)

受到元器件、材料、工艺及成本的限制，单体设备的可靠性存在上限。在系统层面上，对于超过单体设备可靠性上限要求的，可以通过冗余技术来满足可靠性指标要求。铁路行业有一系列的可靠性标准，通过量化指标对系统性能进行评估，指导系统架构及软硬件设计。MTBF(平均故障间隔时间)是最常使用的可靠性指标之一。按照EN 50126标准[1]， MTBF被定义成系统保持工作状态的平均持续时间，其本质上是指MTBSF(运营服务的平均无故障间隔时间)。通过冗余设计，可保障单点故障不影响系统服务(即实现故障容错)，系统保持持续服务以满足MTBSF。

对安全的传统定义是“免于不可接受的风险”。安全完整性SIL(Safety Integrity Level)是与可靠性相关的一个概念，定义为“安全相关系统在所申明的运行环境中和所申明的时间段内的条件下完成所要求安全功能的能力”[1]。安全完整性和可靠性是对城市轨道交通(以下简称“城轨”)信号系统的两大性能要求。基于安全完整性和可靠性的系统设计对单点设备故障进行容忍。这类故障需要在设计之初明确定义，故障场景是限定的，容错能力有限。在城轨逐步由全自动运行向自主运行发展过程中，信号系统已不能满足更高的可靠性要求。

系统韧性理论是将韧性概念引入复杂系统的研究成果[2-3]。系统韧性理论立足于运营的角度来对系统容错能力进行观察，与基于设备RAM(可靠性、可用性、可维护性)指标提升来间接提升容错能力不同，系统韧性理论要求系统从容错本身来寻求改善措施，要求系统对故障、扰动、风险进行实时监督，基于监督结果动态采取相匹配的容错响应。本文对系统韧性理论在城轨信号系统设计中的应用进行研究，并以城轨智能调度系统为案例来说明这一方法的有效性。

1 系统韧性理论

韧性(Resilience，中文研究者也采用“弹性”)一词来源与拉丁语动词resilire(弹回)，指物体在被挤压发生变形后，恢复到其正常尺寸和形状的能力。其内涵就是在受到扰动后恢复正常的能力[4]。研究者将这一力学概念首先引入生态系统，后来又广泛应用于社会领域、经济领域和安全工程领域[5]。一个源自国防领域的韧性定义是：一个实体(资产、组织、社区或地区)的能力，能预测、抵制、吸收、应对、适应和从自然或人为干扰活动中恢复。这就要求具有韧性的系统应该具备3种能力：击退、抵抗、吸收破坏的能力(自然或人为破坏)，从破坏中恢复的能力(灾难或灾难事件)，适应新的或变化的条件(人为威胁或自然灾难)的能力[3]。本文认为，还应具备的第4个能力是预测能力，即对发生的破坏、扰动进行监督识别，并预测其影响的能力。

在安全苛求领域，文献[5]提出了韧性工程的概念，通过系统韧性来实现系统的安全，并将韧性定义为：系统所具备的在发生变化和扰动前/时/后调整其功能的自有能力，由此系统能够在预期的条件和非预期的条件下都能保持运行[5]。既有的安全观是想办法减少系统发生故障的概率，而韧性工程的安全观则将安全工作的目标调整为想办法增加系统正常工作的概率，这样即能保障安全，又能提升系统的效能，实现对系统安全与效能的兼顾。

系统容错的概念是指在出现故障时系统能够继续实现其既定功能的能力[6]。容错、安全完整性和韧性的概念比较如表1所示。

由表1可见，韧性概念涵盖的范围最大，其次是容错，最小的是安全完整性。可以通过韧性或容错设计来满足完全完整性要求。韧性实现的目标是“恢复并适应新的或变化的条件”，既有恢复到既有功能的能力，也有适应外部条件变化而产生新的功能的能力。而容错则是实现既定功能的能力，安全完整性则仅要求完成安全功能。对于运行条件而言，韧性也更加宽泛，包含了预期与非预期的条件；安全完整性则是在所申明的运行环境和所申明的时间段内，能保证系统会做出安全的响应，而在非所申明的运行环境(非预期的条件)中并不能保证。

表1 容错、完全完整性和韧性概念比较

另外，安全完整性没有对系统持续工作能力的直接要求，系统的可持续工作能力间接地由“所申明的运行环境和所申明的时间段”这一与可靠性性能直接相关的要求所决定。

为指导设计，系统韧性应通过量化的手段进行评估[7]，对系统韧性进行度量。系统韧性的量化评估示意图如图1所示。

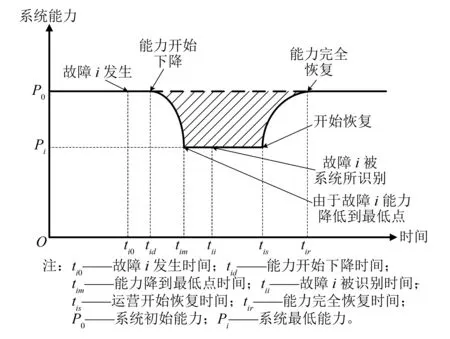
图1 系统韧性的量化评估示意图Fig.1 Diagram of quantitatively estimated system resilience

1) 保护时间Tip：是系统容忍故障i而不导致能力降低的持续时间。Tip=tid-ti0。

2) 退化时间Tid：是在受到故障i的影响后系统在能力最低状态持续的时间。Tid=tim-ti0。一般情况下，假设Tid为0。

3) 识别时间Tii：是系统识别出故障i的时间。Tii=tii-ti0。这一时间不一定会大于Tid。系统可以在能力降到最低前就识别出故障。

4) 恢复时间Tir：是系统从故障i发生到恢复正常运行所需的时间。Tir=tir-tis。一般情况下，假设Tir为0。

5) 能力退化量Pid：Pid=P0-Pi。

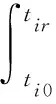
Pil越小，系统韧性越好。需要注意的是，这里的Pil仅考虑了单次故障，如果要综合衡量一段工作周期内多次故障的综合损失，则需要将每个故障导致的Pil进行求和，即∑Pil。Pil还可以用于评估不同故障导致的能力损失，从而对故障进行分级。可靠性标准强调的是延长MTBF并缩短MTTR(平均修复时间)。在修复期间(tir-ti0)，系统是处于下线状态，即Pi为0，如果套用Pil的计算方法，应该尽可能地缩短MTTR的时间。此外，可靠性标准考虑的故障偏向于硬故障，即故障后能力立即降低到0(Tid=0)。

2 基于系统韧性理论的城市轨道交通信号系统设计模型

既有的城轨信号系统是容错的“故障-安全”系统。当发生影响安全的故障时，这样的系统可以采取“故障-持续运行”“故障-降级”和“故障-停机”3种不同的响应形式。

1) “故障-持续运行” 响应形式：当出现故障时，系统继续工作，提供能力不损失。

2) “故障-降级”响应形式：当出现故障时，系统继续工作，提供能力有一定损失，但能够保持安全状态。

3) “故障-停机”响应形式：当出现故障时，系统停止工作，提供能力全部损失，转换到一个确定状态以维持安全。

从“故障-安全”角度考虑，一个韧性的信号系统应避免“故障-停机”的响应形式。如果没有人工的介入，“故障-停机”会导致Pil→∞。如果按照RAM设计思路，信号系统设计应设法降低单体设备的MTTR，并延长MTBSF、控制∑Pil。MTBSF和MTTR受到基础技术条件和现场工作条件限制，提升有限。然而，按照系统韧性理论，信号系统可通过增强系统韧性的技术手段来控制Pil，这样的技术手段组合构成了新的韧性系统设计模型(见图2)，其中包括：①识别故障扰动——对导致能力损失的故障或扰动进行识别；②影响预测——对故障和扰动进行分类，并依据历史数据和状态信息综合预测其影响，例如预测故障的处理时间；③故障抵制——在系统中留有能力补偿的空间或容错机制，一旦发生故障或扰动，系统利用补偿空间或容错机制对故障进行抵制：④恢复控制——通过自恢复或远程恢复技术，恢复系统能力；⑤能力损失评估——对发生的能力损失进行在线评估，并对恢复措施进行评价。

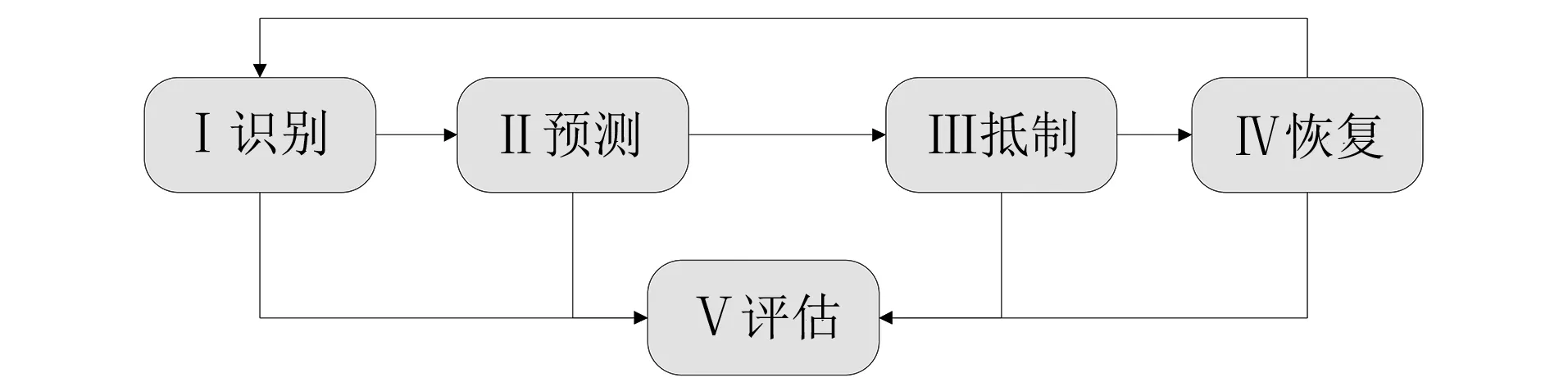
图2 韧性系统设计模型Fig.2 Resilience system design model

在韧性系统设计模型中，能力损失的在线评估是与传统的系统设计模型差异最大的部分。在传统的可靠性设计模型中，由操作人员完成能力损失评估，因此需要大量的人工介入以保持运营；能力损失评估之后，再对故障进行调查分析，并针对性提出改进措施，以提升系统MTBSF。本文以城轨智能调度系统为案例来验证韧性系统设计模型的有效性。

3 基于系统韧性理论的智能调度系统设计案例

当前FAO(全自动运行)实现了从列车唤醒、运行到休眠的全过程自动化，但并未实现全过程无人化，工作人员还需要对故障或应急事件进行介入处理。为满足未来城轨发展需求，信号系统要从更高层面上来满足安全要求。为此，系统设计考虑的边界更大，要能够更多地站在“满足运营需求”的高度来考虑故障问题，实现最低限度的人工介入，达到“运营无人化”的最终目标。

3.1 系统能力指标

首先定义关键运营服务质量(即系统能力)指标：车站到发间隔失衡率βs和发车间隔损失率σs。在运营恢复期间，从故障发生后第一个扣车的车站至终点(或小交路折返)车站的各个车站(受影响车站集合S)，列车到站时间间隔a的最大值与最小值之差与二者之和的比值即为βs(s∈S)。βs越大，则对应车站的到发间隔越不平衡。其计算公式为：

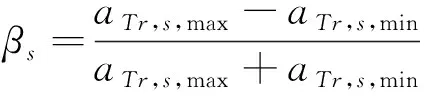
(1)

式中：

Tr——运营恢复时间段。

Tr从故障发生的时刻td开始计算，直到由该故障所引发的车站扣车、跳停、赶点不再发生时刻tr为止，即所有列车都恢复正常运营为止。

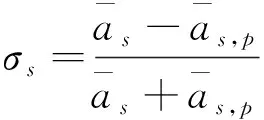
(2)

由此可得服务质量损失值Pl：

[Wβ×(1-βs)+Wσ×(1-σs)]}Tr/To

Wβ+Wσ=1

(3)

式中：

Ws——车站权重，客流较密集的车站、换乘站和终点站的权重较大；

Wβ和Wσ——分别为车站βs权重和σs权重值。

To——全天运营时长。

计算时，为避免Pl对Tr过于敏感，对Tr相对于To进行了归一化处理。

列车运行中，如发生影响运营的故障，例如在区间运行中发生车门关好并锁闭状态信号丢失的故障，既有信号系统基于 “运行”安全，会立即控制列车区间停车，即采用“故障-停机”响应形式来满足安全完整性要求，然后由人工处理故障并保证运营安全。故障导致的晚点影响则会在线路上快速传递，尤其是在高峰运营期间，传递速度更快，影响更为显著。为恢复运营，调度人员需要人工调整线路上的多列列车的运行。

以上海轨道交通某条线路的一个具体故障为例，90号班次列车在区间发生车门故障时正值晚高峰(18:20)，为平衡故障车前后列车的运行间隔，调度员对故障列车所在区间的前后9个车站进行连续扣车。故障列车以20 Km/h速度进站，在站台进行清客后列车切除ATP(列车自动保护)回库。该故障造成故障列车后的第一列列车晚点510 s。调度员逐步取消扣车，并让故障列车后的第一列列车连续跳停，并将另一列列车的小交路改为大交路，同时取消了2列列车的运行班次。1 h后，运营基本恢复。

列车发生故障后，通过人工调整手段，可使服务质量逐步从扰动中得到恢复，根据式(3)计算，这次故障导致的服务质量损失值Pl为3.2%。如果把调度人员作为系统的一部分，则包含调度人员的大系统的韧性也可以通过能力损失进行量化评估。而智能调度系统则能替代或部分替代调度人员的工作，对于类似上述案例中的运营扰动，会自动识别、预测、获取恢复控制策略。本文将智能调度系统作为信号系统的一部分，构建新的韧性信号系统。

3.2 智能调度系统功能模块

按照韧性系统设计模型，智能调度系统应包含以下功能模块：

1) 故障识别模块：主要根据采集到的实时多源信息对出现的故障进行识别。多源信息来自信号系统及与信号系统有接口的外部系统(例如车辆系统)。故障识别任务包含获取故障类型、故障发生的地点和时间等信息，明确故障源。

2) 初始策略生成模块：当故障处理时间不能预测时，通过初始策略对列车运营进行调整以避免运营危害并减小影响。初始策略的判断依据是故障识别结果、线路站型和当前运营间隔等条件，并通过扣车[8]、速度等级调整等组合措施调整故障列车前后列车的运行。

3) 故障恢复预测模块：对故障列车完成现地处理(如故障隔离)后，有条件地预测故障恢复时间。预测的依据包括故障源、故障列车低速进站距离、故障列车清客时间和故障列车回车辆基地/存车线路径等。如果是与列车运行相关的故障，预测结果则是故障列车退出运营的路径及退出的运行速度曲线；如果是地面的固定设备故障，则直接进行恢复策略生成。

4) 恢复策略生成模块：依据预测结果，对扣车、跳停、备车替开、速度等级调整和变更交路这五种措施不同组合下[9]的Pl进行最优化计算，然后确定Pl最小的恢复策略。

5) 服务质量评估模块：对恢复策略实施的效果按照服务质量进行评估，并积累数据形成经验库；当数据量达到一定要求后，通过经验库挖掘算法对恢复策略算法进行参数(例如Pl计算公式中权相关参数的重值)优化，以提升策略生成效率。

3.3 仿真验证

在实验室环境下，采用测试平台(见图3)对智能调度系统进行设计验证。其中，ATS(列车自动监控)中加载了该线90号班次列车(见3.1节)故障当天的真实时刻表数据，并模拟当天的真实故障。采用人工调度和智能调度的列车运行图如图4所示。

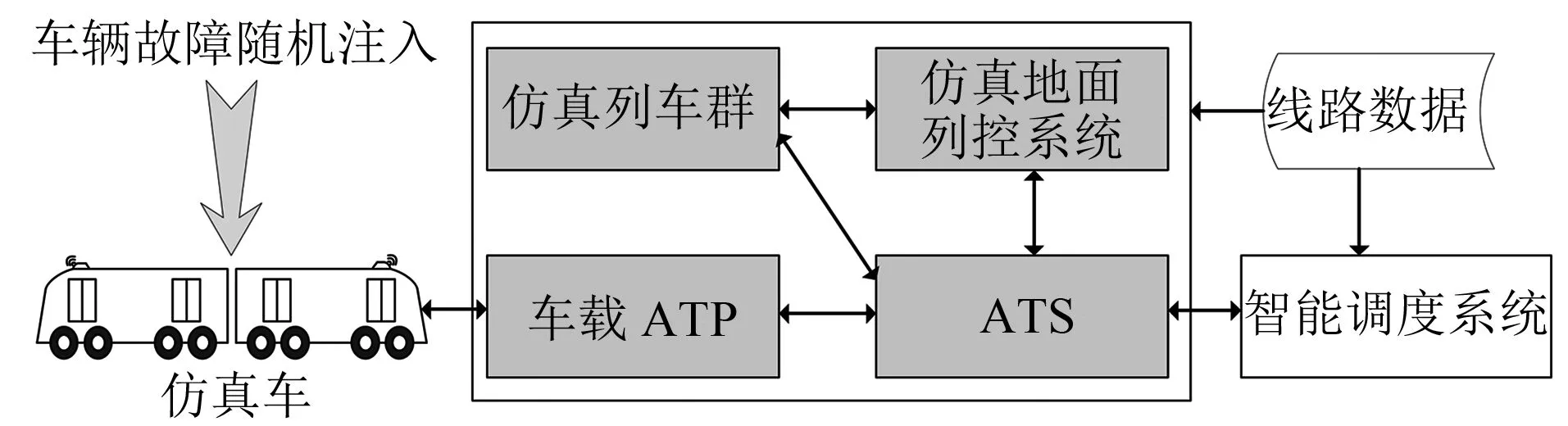
图3 智能调度系统测试平台示意图

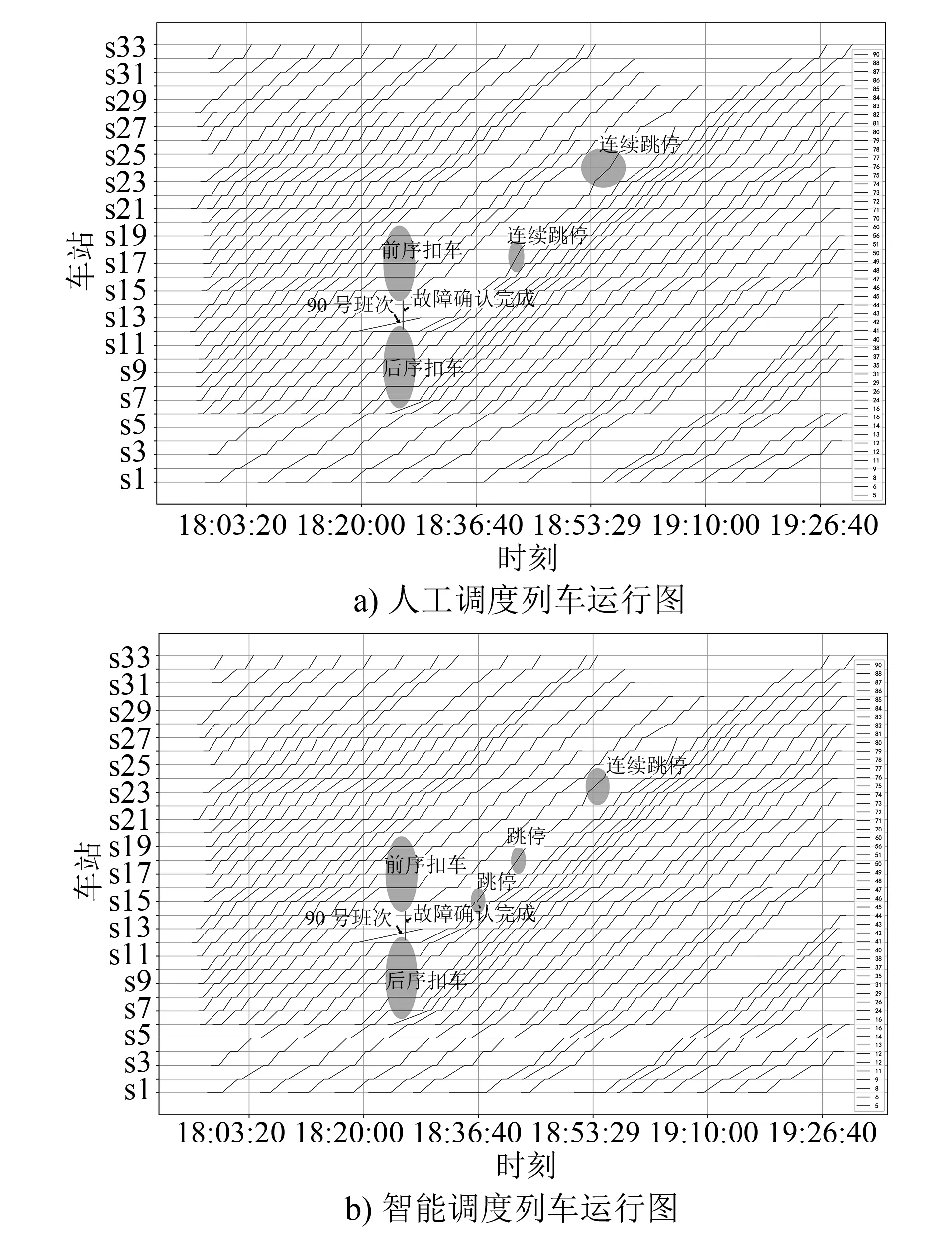
图4 人工调度与智能调度下的列车运行图截图

在所述故障情况中，s15为第一个发生扣车的车站，s28为小交路折返车站。该列车发生故障后的服务质量损失计算结果见表2。由表2可见：采用智能调度的βs，除车站s15、s26、s27和s28外，多数车站的都大大小于人工调度下的βs，也就是智能调整能得到很好的到发均衡性；由于案例中没有采用加车的策略，因此智能调度下的σs与人工调度下的σs差异不大。按运营时间17 h计算，Wβ和Wσ采用等值，通过智能调度下的智能调整，根据式(3)计算，故障导致的服务质量损失值Pl减小到2.5%(主要贡献来自于故障列车退出运营)。由此可见，与人工调度相比，智能调度系统具备更高的韧性，大大减轻了人工的工作强度。

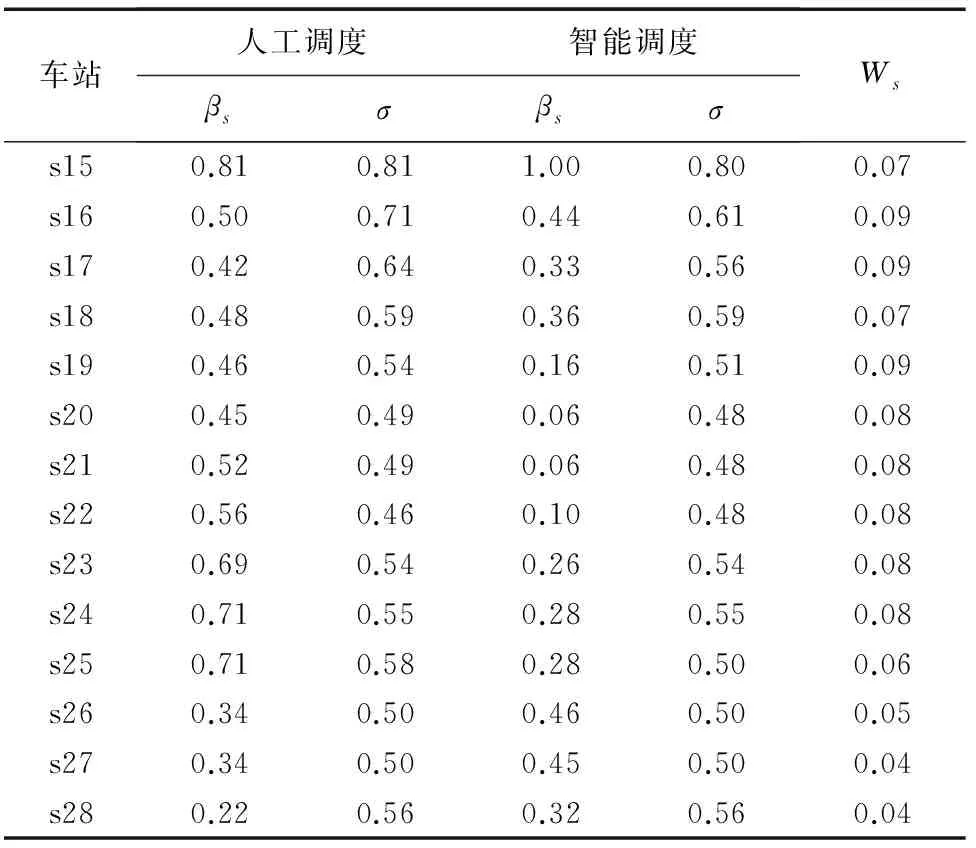
表2 列车发生故障后的服务质量损失计算结果

4 结语

城轨信号系统的自动化等级越来越高，系统管控能力及范围越来越大，人参与的操作越来越少，系统处理非预期事件或故障的能力需要支撑这样的变化，以确保故障下安全持续运行。本文基于韧性系统设计模型进行系统设计，从扰动的识别、预测，以及通过最小化损失值为目标进行优化计算获得恢复控制策略等几个方面进行系统构建，开发出智能调度系统。仿真计算验证了该方法的有效性。

本文只是应用韧性理论指导系统开发的初步探索，为开发更强壮的韧性系统，还需进行更多的研究工作。例如：对多源信息进行时间校准及对信息可信度进行交叉检查；发展人机友好系统，使系统操作更便利及易学易用，并能有效防止人为错误；核心设备的健康状态自诊断及故障自修复，等等。