基于自适应粒子群算法的轨下基础病害识别*

伍伟嘉 杨 俭 袁天辰 邵志慧

(上海工程技术大学城市轨道交通学院，201620，上海∥第一作者，助理工程师)

轨下基础结构作为轨道系统重要的承载结构，其作用是将高速列车运行所产生的冲击载荷传递给路基并实现减振效果。随着我国铁路列车运行速度的增加和承载能力的增大，轨下基础必然会承受更大的冲击载荷，而轨下基础病害将会随着轨道系统运营时间的推移逐渐显现，进而威胁行车安全。因此，实现对轨下基础病害快速且高效的诊断和识别是保障列车安全运行的关键。

轨下基础病害识别的首要问题是如何获取轨下基础结构处于病害状态时的故障特征。近年来，小波分析因具有多尺度特性而被国内外学者广泛应用于机械结构和大型土木结构故障诊断领域，特别是故障特征提取方面。文献[1]利用小波变换和奇异值分解提取了水电机组振动的故障特征，并采用概率神经网络算法对所提取到的特征向量进行分类，具有较高的分类准确率。文献[2]基于集成经验模态分解和可调Q-因子小波变换实现了对滚动轴承早期故障的特征提取。由于小波变换没有对振动信号的高中频部分进行分解，导致提取到的特征可能无法完全反映轨下基础结构病害的故障特征信息。为了避免由于小波分解本身分析频段所带来的问题，文献[3]将小波包分解运用到了滚动轴承的故障诊断中，并成功判断出了滚动轴承的故障类型。

在提取故障特征信息后需要对故障模式进行识别，相较于神经网络算法，SVM(支持向量机)算法在处理高纬度、小样本和非线性数据方面有较大的优势，且其还具有很强的自学能力和泛化能力。但SVM算法中对于参数的选择极大地影响了故障识别分类的准确率，因此国内外学者采用智能算法优化SVM参数，如GA(遗传)算法、蚁群算法和网格搜索算法等。但上述这些优化算法存在一些不足之处：GA算法参数较多且寻优速度慢；蚁群算法计算量大且不适用于复杂问题；网格搜索算法运算时间会随着搜索步长的减小而陡增。粒子群算法不仅收敛速度较快，且在解决复杂的非线性问题上有较好的表现。针对轨下基础病害识别，本文利用小波包分解对轨下基础病害振动信号进行三层分解，并提取分解后的底层能量作为后续故障分类的输入，利用自适应粒子群算法联合SVM算法对病害进行识别，以较好地识别出不同的轨下基础病害。本文研究可为轨枕的故障诊断以及预测提供理论及参考依据。

1 车辆-轨道耦合动力学模型与病害模拟

1.1 车辆-轨道耦合动力学模型

采用如图1所示的车辆-轨道垂向耦合动力学模型，其中车辆系统是由车体质量mc、转向架质量mT、轮对质量mw组成的一个多刚体系统，并以速度v在轨道模型上运动，考虑车体和前后转向架的沉浮运动自由度(zc,zT1,zT2)与点头运动自由度(βc,βT1,βT2)，以及4个轮对的垂向运动自由度(zWo,o=1,2,3,4)，则车辆系统的运动方程为：

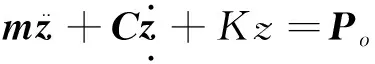
(1)

式中：

m、C、K——分别为车辆系统的质量、阻尼和刚度矩阵；

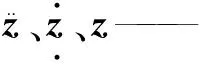
Po——系统力向量。

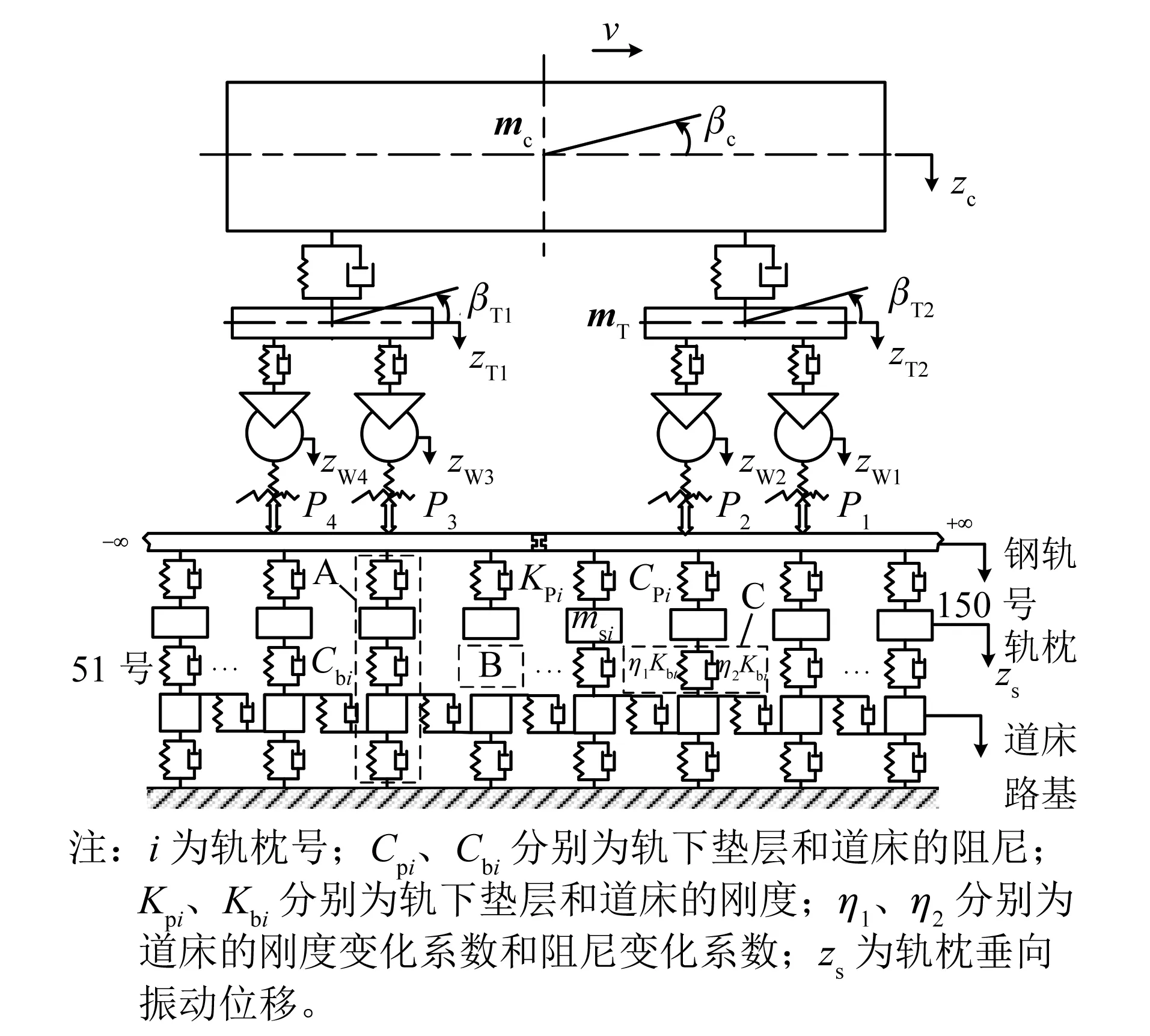
图1 车辆-轨道耦合动力学模型(含病害)Fig.1 Vehicle-track coupling dynamics model (including diseases)

轨道系统由钢轨、轨下基础(包括轨枕和道床)以及路基组成，其中钢轨可以视为连续弹性离散点支撑上的无限长Euler梁，轨下基础可模拟为双质量、三层弹簧-阻尼振动模型(见图1中的模型A)，并按轨枕间距沿纵向离散。本文不涉及钢轨、道床和路基的振动方程，具体可参考文献[4]。文献[5-6]的研究表明：通过改变模型中的Cbi和Kbi可以模拟轨下基础病害，例如：轨枕完全空吊工况(见图1中的模型B)即完全失去工作能力，可设Kbi=Cbi=0；对于道床板结或松散工况(见图1中的模型C)，则设Kbi,ne=η1Kbi，Cbi,ne=η2Cbi，对于不同程度的病害，η1、η2的取值范围为[0.1,10.0]。

1.2 轨下基础病害仿真

采用Matlab软件建立车轨耦合模型，时间步长设置为1×10-4s，取轨道长度L=120 m，轨枕间距Ls=0.6 m，选取位于轨道系统中心位置的51号—150号共100个轨枕截面单元，以100号轨枕为振动响应分析对象。不同工况下的轨下基础模拟参数如表1所示。根据表1的仿真工况，以列车行驶速度为200 km/h为例，轨枕在不同工况下的振动加速度时域谱和功率谱仿真结果如图2所示。

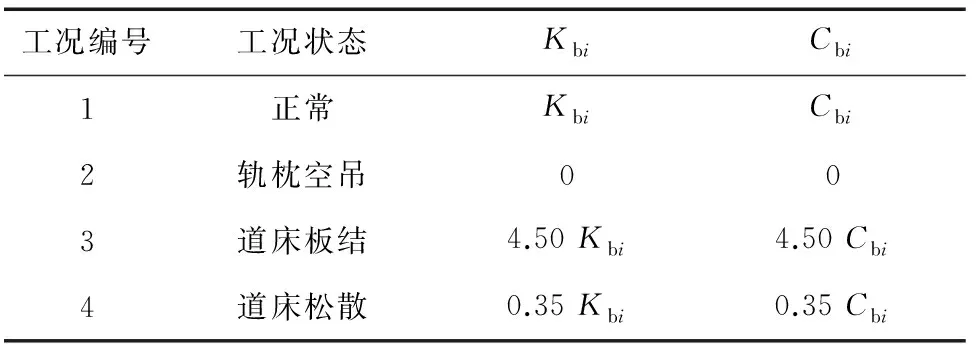
表1 不同工况下的轨下基础模拟参数

由图2 a)和图2 b)可知，轨枕空吊工况下的轨枕振动加速度的幅值比正常工况下要大很多，而从功率谱方面来看,其在100～102Hz频率范围内有明显的变化；从图2 c)—图2 f)中可以看出，道床板结和道床松散工况下的轨枕振动加速度较正常工况变化不是特别明显，而从功率谱方面来看，其在频率低频区变化不明显，在频率高频区变化稍有区别。故需要对轨枕振动加速度进行特征提取，且要求特征提取方法既可以反映轨枕振动加速度在时域上的变化，又可以体现轨枕振动加速度在频域高频和低频区域的特征。

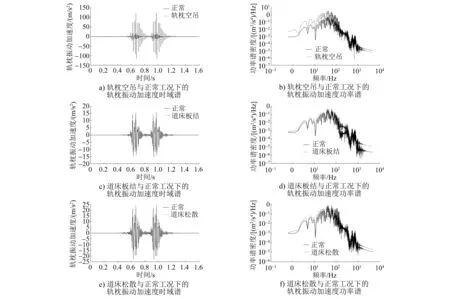
图2 列车速度为200 km/h时轨枕在不同工况下的振动加速度时域谱和功率谱仿真结果

2 基于SVM的病害特征识别

2.1 基于粒子群算法的SVM参数优化

SVM算法是一种用于解决凸二次优化问题的机器学习算法，其核心内容是找到一个分类超平面并将其作为决策曲面，进而最大化正反例之间的隔离边缘。相较于其他人工智能算法，SVM算法在解决高维度、小样本，以及非线性模式识别方面有很大的优势。PSO(粒子群优化)算法是一种根据鸟类捕食行为所提出的群体智能算法，与GA算法相比，PSO的SVM参数寻优方法不需要进行选择、交叉、变异等复杂操作，具有收敛速度快、寻优精度高等特点。因此本文利用PSO算法对SVM进行参数寻优。

PSO算法的基本原理为：在n维空间中随机地产生一些粒子，每个粒子代表了所求优化问题的一个潜在最优解，每个粒子的特征信息用位置x、速度v及适应度三项指标描述，其中适应度指标由目标函数确定，用于反映某个粒子与其他粒子之间的优劣程度；每个粒子按照特定的方程以不同的速度和位置进行移动，在移动过程中每个粒子都会计算该位置的适应度值，从而得到该粒子的局部最佳位置；通过粒子之间的交互协作和信息共享，可以获得整个粒子群体的最优适应度值和最佳位置，每个粒子在移动过程中也会根据个体和整个群体的最佳位置及适应度，动态地调整、更新位置和速度，通过逐步迭代最终实现最优解的寻找。

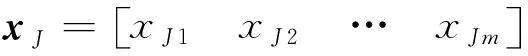
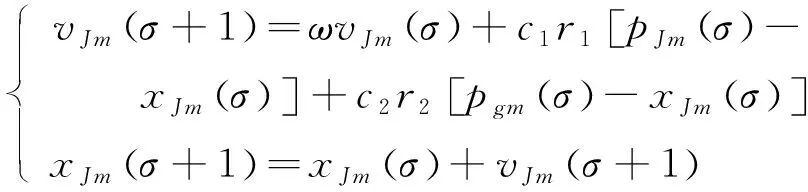
(2)

式中：

pgm——m维下的种群全局极值；

σ——种群进化代数；

ω——惯性因子，通常取为0.8；

c1、c2——加速因子，取值范围为[0,2]；

r1、r2——分别为两个相互独立的随机数，取值范围为[0,1]。

基于PSO算法对SVM进行参数寻优的算法流程如图3所示。

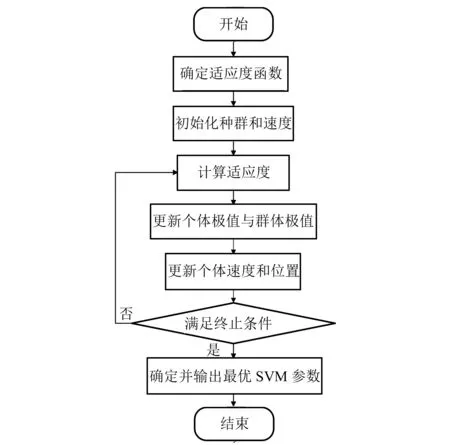
图3 基于PSO算法优化SVM参数的算法流程图

2.2 自适应粒子群算法参数优化

为了进一步加快PSO算法的收敛速度，采用一种自适应变化参数为c1、c2、ω的PSO算法，即APSO (自适应粒子群) 算法。APSO算法主要利用进化状态评估(ESE)将种群的进化细化为搜索、发现、收敛和跳出等4个阶段，结合自适应变化参数对PSO算法进行改进。

在PSO算法中，ω的取值会影响粒子的搜索能力，其值越大，局部搜索能力越弱；其值越小，全局搜索能力越弱。由此可知，在搜索阶段时需要ω的取值较大，而在发现阶段时需要ω的取值较小，故ω的取值需要随着进化状态的改变而改变，可以表示为：

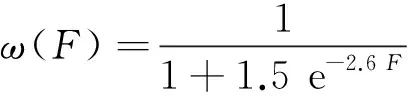
(3)

式中：

F——进化因子，∀F∈[0,1]。

c1、c2是调整粒子朝着局部和全局最佳位置运动的步长变量，因此其也需要随着进化状态的改变而改变。在搜索阶段时，需要搜索到尽可能多的个体最优值，即较好的局部搜索能力，此时需要增大c1并减小c2，以避免算法陷入局部最优；在发现阶段时，粒子利用周围的局部信息使种群向局部最优位置移动，此时需要小幅增大c1并小幅减小c2，以避免过早收敛；在收敛阶段时，种群已经抵达全局最优位置附近，此时需要同时增大c1和c2，以引导其他粒子向其聚集；在跳出阶段时，当前区域的局部最优粒子跳出并远离所在的聚类，快速向新的较优区域移动，同时该聚类中的其他粒子也会跟随该局部最优粒子快速移动，此时需要减小c1并增大c2。

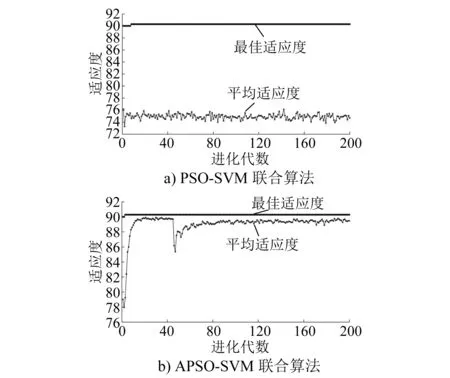
图4 适应度曲线Fig.4 Fitness curve

2.3 基于APSO-SVM算法的轨下基础病害识别

本文基于APSO-SVM联合算法对轨下基础病害进行识别。将由1.2节仿真获得的不同工况条件下的轨枕振动加速度数据分成训练集和测试集，其中：前90组数据作为训练集；后10组数据作为测试集。首先对二者进行三层小波包分解并计算最后一层的能量，然后将所得到的特征向量集合进行归一化处理，最后将不同工况的特征向量集合输入SVM算法。为了验证APSO-SVM联合算法的有效性，采用PSO算法优化SVM参数，将其作为对照组。利用APSO-SVM联合算法和PSO-SVM联合算法进行轨下基础病害识别，其适应度曲线和分类识别结果分别如图4和图5所示。同时，为了验证APSO-SVM联合算法的鲁棒性，在车速为100～140 km/h条件下，利用APSO-SVM算法获得的病害识别准确率结果如表2所示。

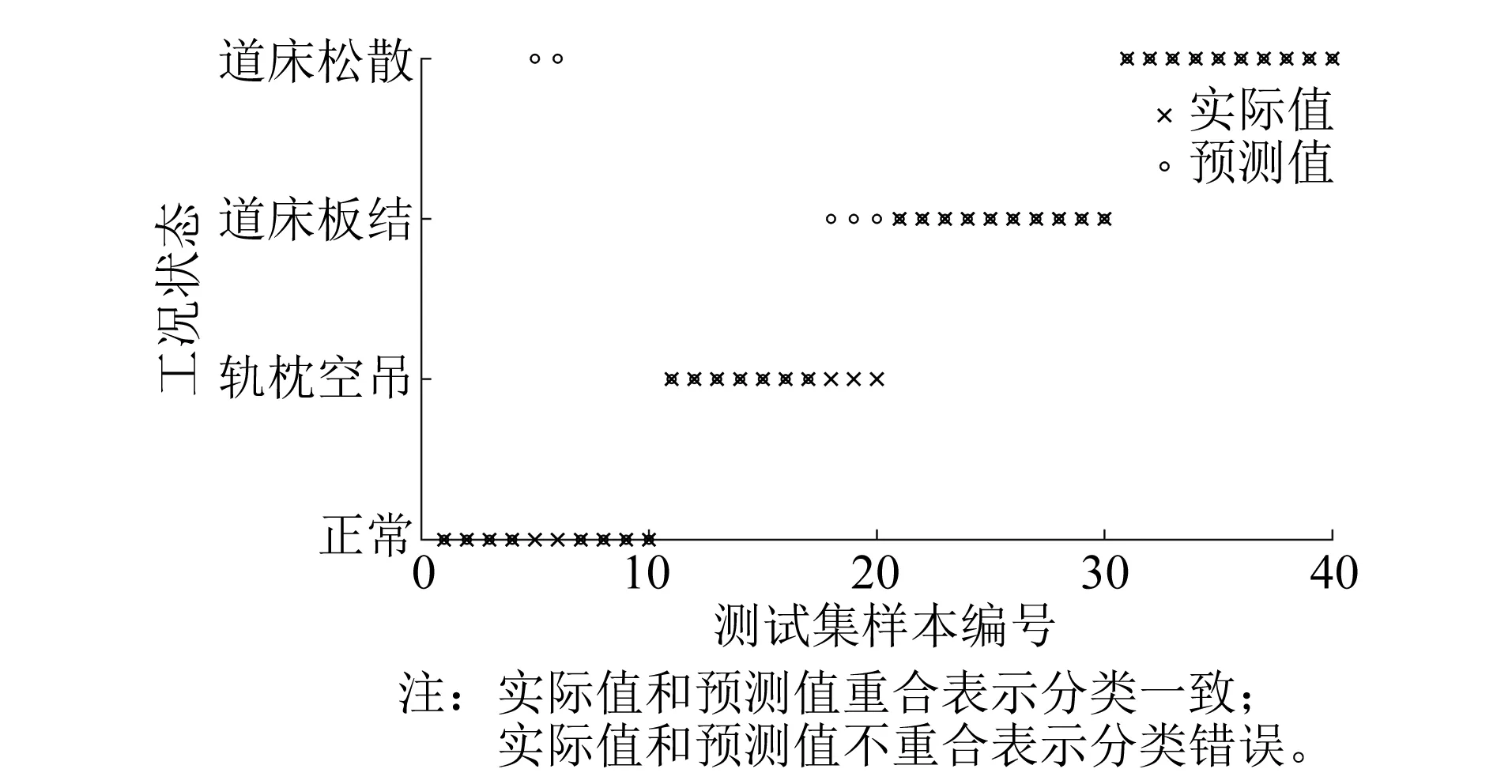
图5 APSO-SVM分类识别结果Fig.5 APSO-SVM classification and recognition results

表2 不同车速条件下的病害识别准确率结果

由图4可知，PSO-SVM联合算法的种群在第10～15代之间就收敛了，而利用APSO-SVM联合算法的种群在第5代左右就已经收敛，并且前者的运算时间为1 464.8 s，后者的运算时间为1 046.92 s，说明利用APSO-SVM联合算法减少了收敛时间。由图5可知，测试样本数量为40个，有35个测试样本的预测值与实际值重合，分类准确率为87.5%(35/40)，说明APSO-SVM联合算法可以较准确地对轨下基础病害进行识别。由表2可知，不同速度条件下，APSO-SVM算法的识别准确率均大于等于80.0%，具有一定的鲁棒性。

3 结语

本文基于时频域分析方法提取了轨下基础不同工况的振动加速度特征，采用SVM算法对轨下基础病害进行了分类，并利用APSO-SVM联合算法优化SVM参数。主要获得以下两个结论：

1) 基于车辆-轨道耦合动力学模型对轨下基础病害进行了仿真研究，并对比了不同病害条件与正常工况条件下，轨枕振动加速度的时域谱和功率谱变化情况。研究结果表明：在轨枕空吊工况下，轨枕振动加速度的时域幅值出现了较大的变化；在道床板结和道床松散工况条件下，其变化不明显；不同病害工况下，轨枕振动加速度在高频和低频区域的功率谱有着不同程度的变化。

2) 为了进一步提高PSO算法在优化SVM参数选优时的收敛速度，提出一种自适应粒子群算法。识别结果表明：在保证识别准确率的前提下，所提算法可以有效提高收敛速度；对不同车速条件下的轨下基础病害进行识别，识别准确率≥80.0%，说明所提算法具有较好的鲁棒性。