热层大气密度反演与建模研究进展

雷久侯，李若曦，任德馨，翁利斌，阮海炳

1 中国科学技术大学地球和空间科学学院 中国科学院近地空间环境重点实验室，合肥 230026

2 国防科技大学气象海洋学院，长沙 410015

3 南京信息工程大学遥感与测绘工程学院，南京 210044

0 引 言

热层大气受到太阳辐射、太阳风-磁层-电离层相互作用、太阳能量粒子注入以及低层大气波动等输入能量的综合作用，呈现复杂的时空变化特征（Hargreaves, 1992）.太阳辐射作为热层大气十分重要的能量输入，对热层有着显著的影响（Knipp et al., 2004）.日夜更替造成热层接收到的太阳辐射周日变化、太阳自转导致太阳辐射的27 天周期变化、地球公转引起的季节和年际变化，以及与太阳活动相关的11年周期变化等，这些因素都会显著影响热层大气物理化学性质（Jacchia, 1959a;Kasprzak and Newton, 1976; Paetzold and Zschörner,1961; Sharp et al., 1978）.如图1 所示，以北京地区所在经纬度大气温度和密度为例，低热层温度随高度增加而迅速增加，直至150～200 km 处温度逐渐趋于恒定，称为逃逸层温度.日侧逃逸层温度在太阳活动低年大约为750 K，在高年则可达1 400 K，温度差异接近100%.热层大气密度随高度增加呈指数衰减，而且受太阳活动的显著调制.在600 km 高度区域，热层大气密度在太阳活动高年时比低年时约有两个数量级的变化.耀斑、磁暴等太阳爆发事件可对热层大气造成短时间尺度剧烈的扰动（Bruinsma et al., 2006; Lei et al., 2011, 2012; Liu et al.,2010, 2011; Lühr et al., 2004; Sutton et al., 2005）.低层大气扰动也会通过波动等方式影响热层大气（Yiğit et al., 2016）.

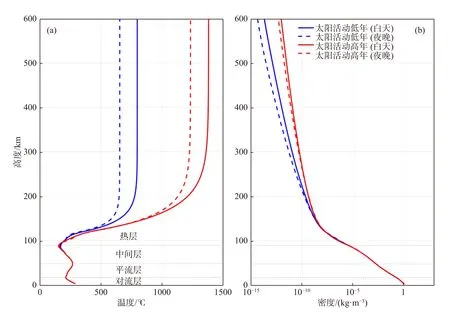
图1 利用MSISE00 热层大气经验模型获得的北京地区所在经纬度（116°E，40°N）大气分别在太阳活动高年与低年的温度（a）和密度（b）随高度分布情况Fig.1 Altitude profiles of atmospheric temperature (a) and density (b) during solar maximum and minimum, based on the MSISE00 model, over Beijing (116°E, 40°N)

研究热层有助于进一步厘清日地相互作用实质，另一方面，热层是人类空间活动的主要区域，在航天工程领域具有重要的应用价值.大部分航天器的轨道，包括神舟、天宫以及各类资源遥感卫星等在内，均位于这个区域.热层大气密度作为热层环境重要的物理参数，对卫星定轨、航天器控制、太空垃圾监测等工程具有十分重要的影响（李若曦，2022；任德馨，2021；翁利斌，2019）.虽然高层大气十分稀薄，但是对于高速运行的人造航天器来说，也会受到稀薄大气显著的拖曳作用.在轨航天器所受大气拖曳力与热层大气质量密度直接相关.随着高度增加，大气密度呈指数衰减，则大气拖曳力迅速降低.对于300 km 高度的航天器，大气拖曳力可以达到10-5m/s2，而在大约800 km 高度，大气拖曳力迅速衰减至约10-10m/s2（Montenbruck and Gill, 2000）.热层大气的拖曳作用可造成航天器机械能减少，轨道高度下降，在无额外动力提升轨道高度情况下使航天器最终陨落.此外，热层大气受空间天气事件影响变化剧烈，航天器轨道也会随之发生显著变化，从而影响航天器控制和预报，增加空间目标碰撞预警的不确定性（Li and Lei,2021a）.因此热层研究对于加深人类对日地空间系统的认识有着重要的科学意义，在航天工程领域也具有显著的应用价值.同时，热层作为电离层的背景大气，由于离子-中性相互作用等过程，热层大气的变化能够引起电离层发生相应的改变，因此，研究热层大气变化也是深入认识和理解电离层变化特性的基础.

获取有效观测数据是热层研究的基础.地表附近的大气参数可以通过温湿度计、气压计以及风速计等设备十分便捷地测量.中间层和低热层大气参数则可以通过卫星遥感、雷达、探空火箭以及气象气球等设备进行探测（张晓芳和严卫，2007）.然而，对于200 km 以上的大气，以上观测手段都难以有效测量.因此，对于热层大气的观测数据十分稀少.目前，热层大气密度探测的主要方式是基于航天器轨道或者星载加速度计数据进行密度反演.基于卫星轨道数据的热层大气研究开始于上世纪五六十年代（Priester et al., 1967; Prussing and Conway, 1993; Thomson, 1986; Vallado, 2001）.随着人造航天器的增多，北美防空联合司令部（NORAD）开始以两行数据（TLE）的形式发布空间目标的轨道跟踪数据.很多研究人员基于TLE 数据反演了长时期的热层大气密度，揭示了热层大气的气候学演化规律（Emmert, 2009; Marcos et al., 2005; Picone et al., 2005）.随着星载GPS 接收设备和加速度计的发展和应用，基于卫星精密定轨（POD）数据和加速度计数据，可以获取更高时空分辨率和精度的大气密度观测数据.近年来，CHAMP、GRACE、GOCE 以及Swarm 等卫星的高质量大气密度观测结果，已被广泛应用于热层大气研究中，用来揭示热层大气的精细变化特征，并优化大气模式（Bruinsma and Forbes, 2007, 2009, 2010; Li and Lei,2021a, 2021b; Lei et al., 2010; Liu and Lühr, 2005;Liu et al., 2007; Lühr et al., 2004; Ren and Lei, 2020,2022; Ruan et al., 2018; Weng et al., 2017, 2019）.

卫星只能对全球热层大气进行采样式观测，获取时空连续的全球热层大气数据一般依赖于理论或者经验模式计算.理论模式一般基于描述质量、动量以及能量的方程，通过数值计算的方法求解全球尺度的大气参数.理论模型可以模拟大气演化过程及其物理机制，以及获取较为精细的热层大气结构，但其输出的大气参数的绝对值一般与真实结果相差较大，因此理论模式一般用于热层大气机理性研究.经验模式则基于参数化的经验方程，采用观测数据驱动的方式进行参数拟合，虽然物理原理涉及较少，但是输出结果与真实较为接近.经验模式也存在较大误差，在地磁平静时期误差一般约为15%，在磁暴期间则更大（Marcos, 2006）.大气经验模式的误差对于卫星轨道预报、轨道维持、碎片预警以及陨落预报等航天工程具有重要影响（李若曦，2022；翁利斌，2019）.

本文将综述当前基于空间目标两行轨道数据、航天器精密轨道数据以及星载加速度计数据反演热层大气密度的方法，总结目前常用的大气经验模式算法和适用范围，并针对当前最新的模式优化方案进行重点阐述.需要指出的是，最近几年学界在热层大气密度反演与建模研究方面取得诸多进展，但这篇文章主要综合我们近期的三篇博士论文（李若曦，2022；任德馨，2021；翁利斌，2019）的进展和部分成果，因此本文内容难免存在疏漏之处.

1 热层大气密度反演方法

1.1 热层大气密度反演基本原理

航天器飞行高度一般高于200 km.200 km 以上热层区域大气十分稀薄，大气分子平均自由程超过100 m，远大于航天器尺度（刘林，1992）.因此，热层大气以自由分子流的形式与航天器相互作用，产生的拖曳力为：

其中A为 航天器迹向等效横截面积，Msat表示卫星质量，CD代表大气阻尼系数，vr表示航天器相对大气运动速度， ρ为航天器附近的热层大气质量密度.航天器半长轴在切向摄动力的作用下衰减.对于轨道高度较低的航天器，切向摄动力主要为大气拖曳阻力.根据轨道摄动理论，航天器半长轴a在大气拖曳阻力[式（1）]作用下的变化可以表示为（Vallado, 2001）：

其中e、f和n分别指代航天器轨道偏心率、真近点角和平均运动等轨道根数.根据式（1）或式（2），可反演热层大气密度.其基本原理为，通过星载加速度计直接测量或者通过航天器轨道衰减间接计算大气拖曳力，然后根据卫星形态、姿态以及面板材料等参数估计大气阻尼系数CD，最后计算大气密度.

1.2 计算有效横截面积和阻尼系数

根据式（1）反演热层大气密度，需要准确计算卫星有效横截面积A与 大气阻尼系数CD.大气分子与每一个卫星面板发生作用，产生拖曳效应.根据Sentman 模型（Sentman, 1961），可以首先计算航天器每一个面板所受大气拖曳力，再将所有面板所受总的拖曳力叠加.每块卫星面板大气阻尼系数与横截面积的乘积为：

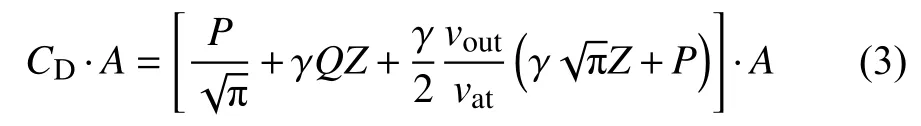
vout表示大气分子流与卫星面板碰撞后的速度，vat为大气相对卫星速度.

S表示vat与大气分子热力学最可几分布速度之比：

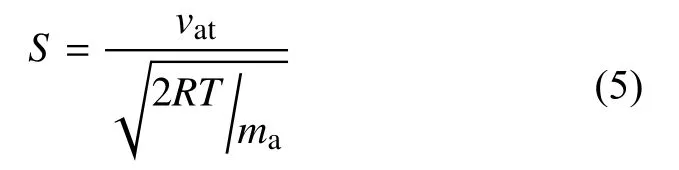
最后叠加航天器所有面板所得结果，得到航天器整体有效横截面积与大气阻尼系数之乘积.如图2 所示，以CHAMP 卫星为例，卫星由13 个面板组成，其有效横截面积与大气阻尼系数的乘积呈现与卫星环绕周期相关的周期性变化特征，最大值约为2.35，最小值约1.95.该周期性变化的主要原因与热层大气昼夜温度和密度差异有关（李若曦，2017）.

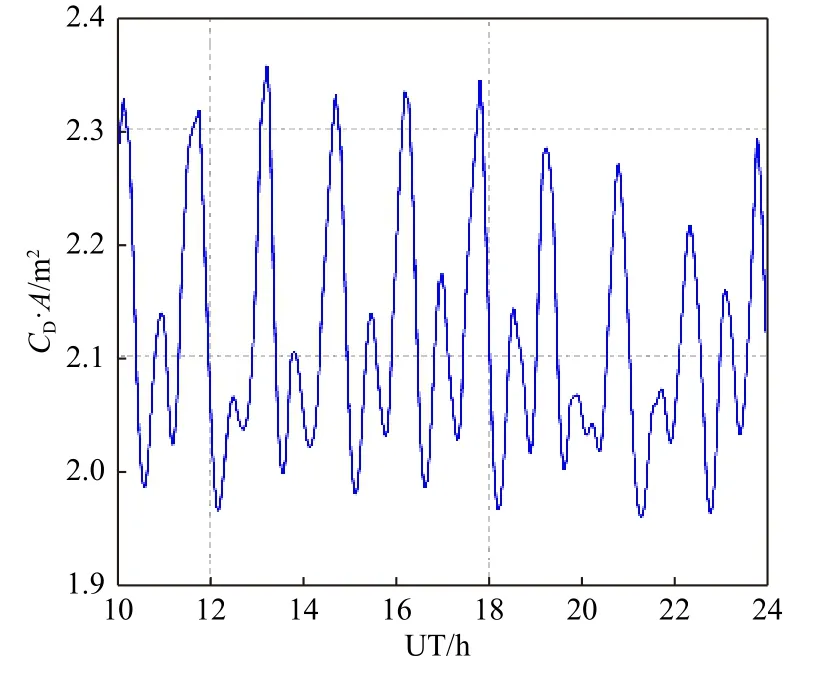
图2 2009年第32 天CHAMP 卫星大气阻尼系数与有效面积乘积的变化Fig.2 The products of CHAMP drag coefficients and crosssection areas during day 32, 2009

1.3 基于两行数据反演热层大气密度

TLE 是美国北美防空联合司令部发布的空间目标轨道跟踪测量数据.该数据库囊括了自1957年至今超过50 000 个空间目标的轨道跟踪数据.TLE 数据包含空间目标编号、轨道根数以及历元时间等信息.基于TLE 数据反演热层大气密度的理论最初由King-Hele（1987）给出，Picone 等（2005）进一步做了优化.根据式（2），理论上通过TLE 给出的历元之间半长轴差即可以反演密度.但是，TLE给出的是航天器瞬时半长轴（或密切半长轴），且地球非球形引力场以及潮汐摄动对航天器半长轴的影响远大于大气拖曳力.不同TLE 历元之间半长轴的变化，除了大气拖曳力的作用，还包括地球引力场导致的周期性变化.因此，Picone 等（2005）采用平均运动（mean motion）的变化反演大气密度.将式（2）中半长轴a用平均运动nM替换得到：

式中B=ACD/Msat，定义为逆弹道系数.F为风影响参数，可表示为航天器位置和速度的函数.相邻两个历元ti至tk之间的平均大气密度(ik)为：

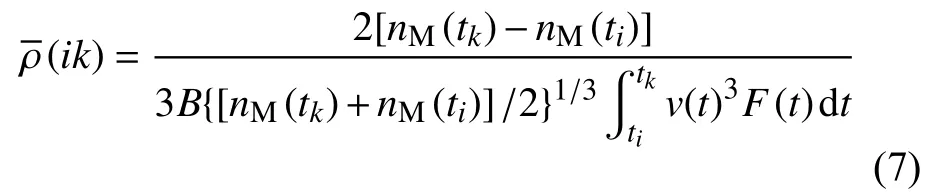
式中nM可以通过TLE 数据直接读取.计算需要计算积分步长上的v(t)和F(t).可以使用SGP4（Simplified General Perturbations 4）轨道积分器（Hoots and Roehrich, 1980）进行轨道外推，从初始历元开始计算每个积分步长上的航天器位置和速度，进而得到v(t)和F(t).基于TLE 数据进行大气密度反演时，一般将大气逆弹道系数近似地设置为常数.图3 展示了基于Starshine 卫星TLE数据的反演密度和MSISE00 结果之比对.Starshine卫星形状为规则球形，逆弹道系数基本保持恒定（Lean et al., 2006）.可以看出TLE 反演密度与MSISE00 结果一致，较好地描述了卫星整个任务期间轨道密度的变化特征.由于TLE 数据时间分辨率低，因此一般只能反演沿轨道2～5 天的平均大气密度.TLE 数据反演密度主要用于研究热层大气的长期变化规律，工程上也被用于大气模式标定工作.

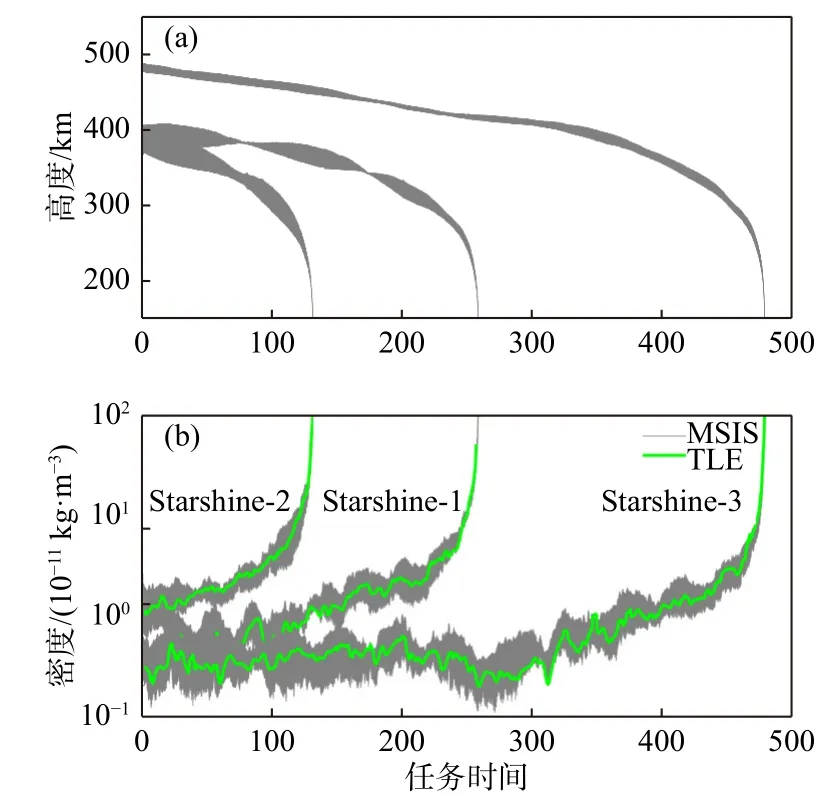
图3 Starshine-1/2/3 卫星轨道高度（a）和基于TLE 数据的反演密度（b）.Starshine-1/2/3 分别发射于1999年5月27日、2001年12月5日和2001年9月29日Fig.3 The altitudes of Starshine-1/2/3 satellites (a) and the TLE-based orbital densities (b).Starshine-1/2/3 satellites were launched on 27 May 1999, 5 December 2001 and 29 September, 2001, respectively

1.4 基于精密轨道数据反演热层大气密度

随着星载导航设备的应用，越来越多的航天器可以被精密定轨.二十一世纪以来，诸如CHAMP、GRACE 以及Swarm 等卫星均具有较高定轨精度.基于这些高精度的航天器轨道数据和精确的力学模型，可以反演获得具有较高时空分辨率的热层大气密度观测数据.本节将介绍几种基于精密轨道数据反演热层大气密度的方法.

1.4.1 插值微分法

根据式（1），可以通过计算航天器所受大气拖曳阻力adrag，反演大气密度.插值微分法的基本原理是对航天器位置矢量进行二阶微分，计算航天器瞬时加速度，然后减去大气拖曳力以外的所有作用力，最终得到大气拖曳阻力（Calabia et al., 2015;Calabia and Jin, 2017）.航天器瞬时加速度计算如下：

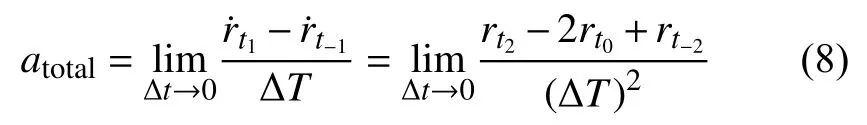
其中，r和r˙分别代表航天器位置和速度.t-2到t2代表相邻的5 个时刻.ΔT代表t-1到t1的时间间隔.为了精确计算航天器所受加速度，时间间隔 ΔT需足够低以降低误差.经过计算比较，该时间间隔被设置为0.05 s.由于航天器精密星历时间间隔一般为几秒到几十秒，因此需要在此基础上进行插值，以获取更短时间间隔的星历.经过插值微分所得航天器瞬时加速度，包括地球重力、潮汐、日月引力、光压、相对论效应以及大气拖曳力等所有作用力.除大气拖曳力，其他作用力使用精确力学模型计算，然后从总的加速度中扣除，得到大气拖曳力，最后进行密度反演：

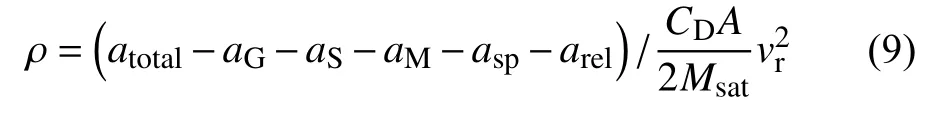
其中aG代表包括地球中心引力、非球形引力以及潮汐在内的地球引力，aS和aM分别指代太阳和月球中心引力场，asp代表光压以及地球反照压，arel代表相对论效应.

微分插值法可以获取较高时空分辨率的热层大气密度，如图4 所示为基于精密轨道数据使用插值微分法获取的GRACE 轨道密度与加速度计结果之比对，可以看出两者基本一致.加速度计数据反演密度具有最高的精度，一般作为参考密度.需要说明的是，插值的准确性依赖于较高的星历数据密度.

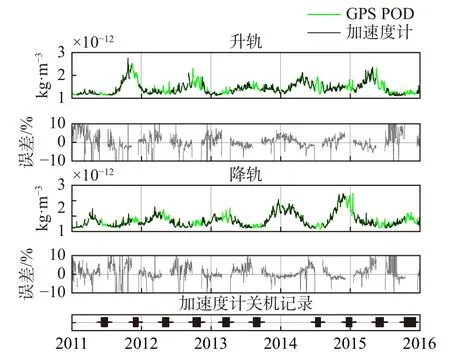
图4 基于GRACE 卫星精密轨道数据以及加速度计数据反演的2011—2016年热层大气密度（修改自Calabia and Jin, 2017）Fig.4 POD-based thermospheric mass densities from 2011 to 2016.The densities derived from accelerometer data are plotted as references (modified from Calabia and Jin,2017)

1.4.2 半长轴衰减法

根据式（2），使用精密轨道数据将方程中e、f和n等开普勒轨道根数由卫星位置和速度替换，只需计算航天器在大气拖曳力作用下的半长轴衰减率，则大气密度可以反演得到.使用半长轴衰减法反演密度最主要的工作就是计算半长轴在大气拖曳阻力作用下的衰减率.下面将详细分析的算法.

对于两个连续的历元（t0,r0,v0）和（t1,r1,v1），对应的半长轴分别为a0和a1.考虑除大气拖曳阻力以外的所有作用力，从历元（t0,r0,v0）外推至t1时刻，得到模拟历元（t1,r1′,v′1），以及对应的模拟半长轴a′1.因此在Δt=t1-t0时间段内航天器半长轴在大气拖曳力作用下的衰减量为a′1-a1（Sang et al., 2012）.需要说明的是，这里采用轨道外推的方法计算半长轴衰减率的原因是，不同时刻的半长轴变化量是大气拖曳力与地球非球形摄动力共同作用的结果，并不能反映大气拖曳力的单独作用.因此，航天器半长轴受大气拖曳力作用的衰减率为：

将上式带入式（2）即可计算热层大气密度.图5 展示了基于精密轨道数据使用半长轴衰减法的反演密度（蓝线），可以看出该结果与加速度计数据结果（红线）具有较好的一致性.

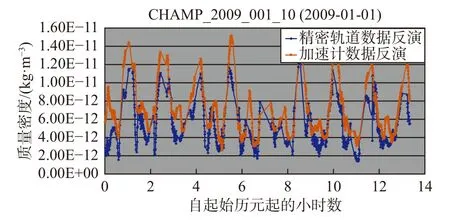
图5 基于CHAMP 精密轨道数据（蓝线）与加速度计数据（红线）之比对（修改自Sang et al., 2012）Fig.5 The comparison of CHAMP orbital density derived from POD data and that from accelerometer data (modified from Sang et al., 2012)

1.4.3 能量衰减法

半长轴衰减法和插值微分法本质上都是利用力学方法，Li 和 Lei（2021b）指出可以基于能量守恒原理反演大气密度.卫星在轨运行，受到中心引力和其他摄动力的作用.该摄动力分为保守摄动力和非保守摄动力.航天器在保守力作用下机械能守恒，在非保守力作用下机械能发生改变.对于低轨航天器，非保守力主要为大气拖曳力、光压以及地球反照压.因此，可以通过计算卫星能量的衰减反演热层大气密度.这种方法不需要进行轨道外推，能够大幅降低计算成本.而且可以根据星历精度选择适当时间步长，对于数据的要求更低，适用范围更广.在轨航天器总机械能可以表示为：

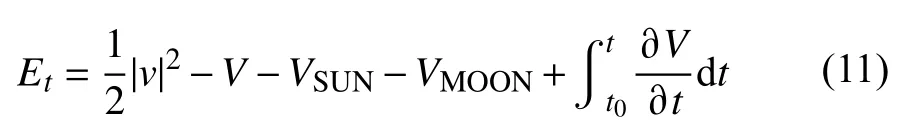
等式右边分别代表航天器动能、地球引力势能、日月引力势能以及时变引力势能，时变引力势能主要由地球自转和各种地球潮汐造成.包含时变引力势和地球重力场在内的航天器总的引力势能变化可以用地球引力对航天器总的做功来表示.航天器在所选取弧段内的能量变化可以写为：

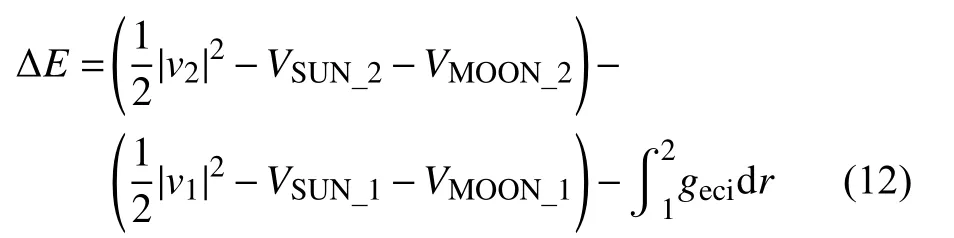
式中geci表示惯性坐标系下的地球引力.下标1 和2分别代表所选取弧段的初末位置.这里机械能的衰减等于总的非保守力做功ΔE=vΔt·an，an表示非保守力加速度.图6 展示了基于精密轨道数据使用能量衰减法反演的GRACE 卫星非保守力加速度与加速度计结果之比对，两者结果较一致.为了得到大气拖曳阻力还需要从非保守力an中减去光压asrp和地球反照压atir等其他非保守力.将所得大气拖曳力带入式（1），即可反演所选取弧度上的大气平均密度.

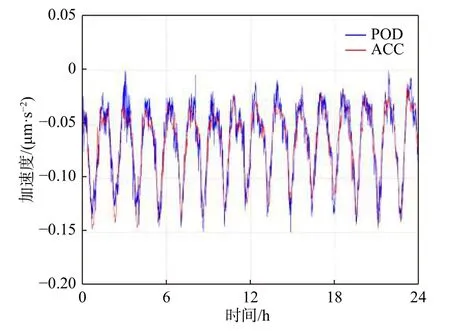
图6 2006年1月1日基于GRACE 卫星精密轨道数据反演得到的非保守力加速度（蓝线）与加速度计测量结果（红线）之比对（修改自Li and Lei, 2021b）Fig.6 The comparison of GRACE along-track non-conservative forces derived from POD data on 1 January, 2006,and those from the accelerometer (modified from Li and Lei, 2021b)

1.5 基于加速度计数据反演热层大气密度

自上世纪六七十年代开始，加速度计开始作为空间载荷进入太空，用于测量航天器所受到的非保守力（Boudon et al., 1979; Champion and Marcos,1973）.二十一世纪以来，一系列低轨卫星如CHAMP、GRACE 等携带更为精密的加速度计进入太空，当前投入使用的星载加速度计主要由法国航空航天研究所（ONERA）制造.表1 罗列了部分ONERA 制造的星载加速度计主要技术指标（Christophe et al., 2015; 马云, 2019; Touboul et al.,2012）.基于这些高精度加速度计数据，研究人员得以获取高时空分辨率、高精度的大气密度观测数据，用于研究热层大气小尺度变化特征，进一步提升大气模式准确性.

表1 ONERA 静电加速度计主要技术指标Table 1 The technical indicators of some on-board electrostatic accelerometers made by ONERA

加速度计数据一般需要在轨标定，以下为基于精密轨道数据的线性标定方法（Bruinsma et al.,2004）：

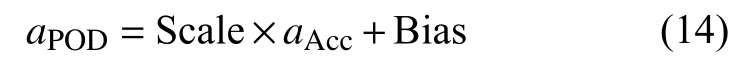
式中，aPOD表示使用精密轨道数据反演的等效非保守力加速度，aAcc代表加速度计测量结果，Scale和Bias 代表尺度和偏差标定因子.根据不同的卫星，选取不同的估计弧长.以GRACE 为例，选择一天作为一个估计弧段，通过最小二乘法估计标定因子，然后使用该标定因子标定加速度计数据.加速度计测量的是所有非保守力加速度，为了得到大气拖曳力还需要减去光压、地球反照压等其他非保守力.根据式（1），热层大气密度可如下得到：

加速度计数据反演密度具有高精度，高时空分辨率等优势.图7 展示了基于GRACE 卫星精密轨道数据（图7a、7b）以及加速度计数据（图7e、7f）反演的2017年9月磁暴期间热层大气密度变化.可以看出精密轨道数据反演的热层大气密度与加速度计反演密度均能描述磁暴期间热层大气的基本变化特征.磁暴期间，极区热层大气密度迅速上升，并激发了大尺度的热层大气波动现象，将扰动传播至低纬区域.加速度计数据反演密度时空分辨率最高，能够给出更为精细的热层大气变化特征.如图7f 所示，加速度计数据反演密度捕捉到了在9月7日平静时期热层大气存在的大尺度波动现象，这可能与当天较高的AE 指数相关.

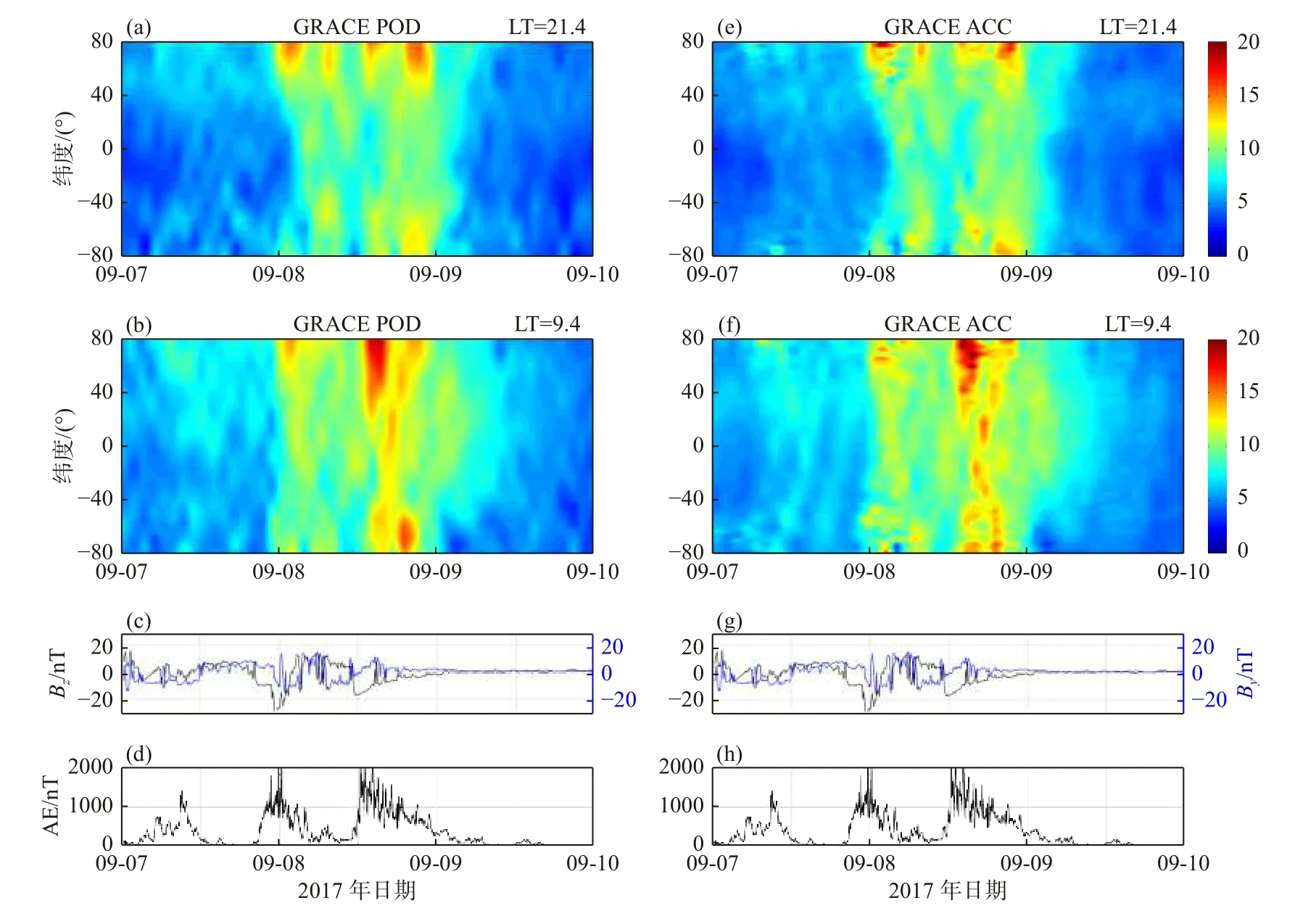
图7 基于GRACE 卫星精密轨道数据反演得到的2017年9月磁暴期间的热层大气密度（a, b）与加速度计反演密度（e,f）.密度单位为10-12 kg/m3.磁暴期间行星际磁场By、Bz 以及AE 指数在子图（c, d）和（g, h）中给出（修改自Li and Lei, 2021b）Fig.7 Thermospheric mass densities retrieved from GRACE POD data and those from the accelerometer data during the 2017 September storm (in units of 10-12 kg/m3).The interplanetary magnetic field By, Bz components, and the AE index are shown in the bottom for reference (modified from Li and Lei, 2021b)

2 常用热层大气经验模式

在航天器定轨、预报以及空间碎片预警等航天工程中，一般使用经验模式计算热层大气密度.本节我们将介绍当前主要的大气经验模式，进一步介绍最新模式优化方法及其结果.根据静力学平衡假设，热层大气密度 ρ随高度h的变化为（Montenbruck and Gill, 2000）：

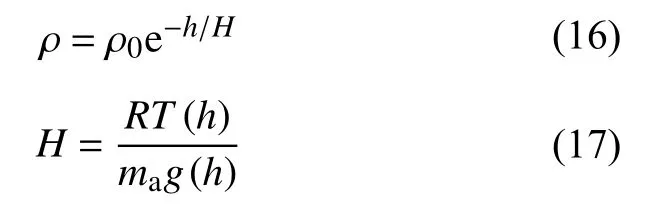
其中 ρ0为参考高度的大气密度，H表示大气标高.R为气体常数，T(h)代表大气温度，ma为大气相对分子质量，g(h)为地球重力加速度.根据式（16）和（17），热层不同种类分子随高度的衰减速率不同，因此不同成分随高度的分布也不同.热层大气经验模式建模的基本原理是基于大量的温度、密度观测数据，拟合半经验半物理的数学公式，得到大气温度廓线，再计算不同分子成分的密度分布.

使用经验模式时，根据输入的太阳、地磁活动指数以及时空信息可以获得热层大气密度结果.由于其易于使用且能够较好再现大气密度变化情况，已被广泛应用于航天工程和科学研究中.目前常用的经验模式主要有Jacchia、DTM、MSIS 等系列模式，经过不断发展改进更新，这些模式的模拟能力和精度也在不断提高.

2.1 Jacchia 系列模式

Jacchia 系列模型从上世纪六十年代开始开发，其发展历程和主要情况如表2 所示.下面以J71 模型为例简要介绍Jacchia 模式算法（Jacchia, 1971;Montenbruck and Gill, 2000）.首先根据太阳活动以及地磁活动计算全球逃逸层温度T∞分布：

表2 Jacchia 系列模式基本情况Table 2 Brief introductions of Jacchia models

其中，T1代表太阳活动周期、半年、季节以及周日变化对逃逸层温度的影响.ΔT∞代表地磁活动对逃逸层温度的影响.温度廓线下边界设置为90 km 高度处温度T0=183 K.在获取整个温度剖面的基础上，可根据温度与密度的函数关系计算密度分布.Gill（1996）建立了以二次多项式表示密度随高度变化的函数，通过插值计算大气密度，可以更为高效的计算全球密度分布.

2.2 MSIS 系列模式

MSIS（Mass Spectrometer Incoherent Scatter）模式基于非相干散射雷达、探空火箭以及质谱仪等观测数据建立，发展历程和主要情况如表3 所示.下面以MSIS86 模式为例简要介绍该模式计算方案（Hedin, 1987）.与Jacchia 模式相似，MSIS 也需要首先计算热层大气温度分布，然后利用各成分对温度的依赖性得到不同高度大气成分分布，最后将所有成分叠加获得大气密度.热层大气温度随高度变化函数为：

表3 MSIS 系列模式基本情况Table 3 Brief introductions of MSIS models

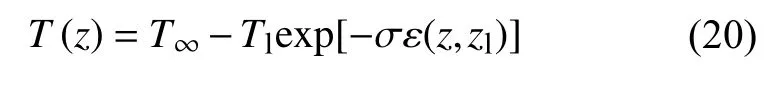
式中T∞=T∞[1+G(L)] 表示逃逸层温度，Tl=Tl[1+G(L)]为120 km 处的大气温度.其中，和分别表示逃逸层平均温度和120 km 处平均温度，在模式中设定为常数，G(L)为经验函数，表征时间、纬度、太阳和磁场活动等参数对大气温度的影响 ，ε (z,zl)=(z-zl)(Rp-zl)/(Rp+zl)，Rp=6 356.77 km.σ=/(T∞-Tl)，其中=[1+G(L)]，为温度随高度变化梯度.

热层大气的密度分布可以看做是大气分子扩散与混合共同作用的结果.假设120 km 高度处不同气体成分的数密度为常数，则成分随高度的变化可以表示为：

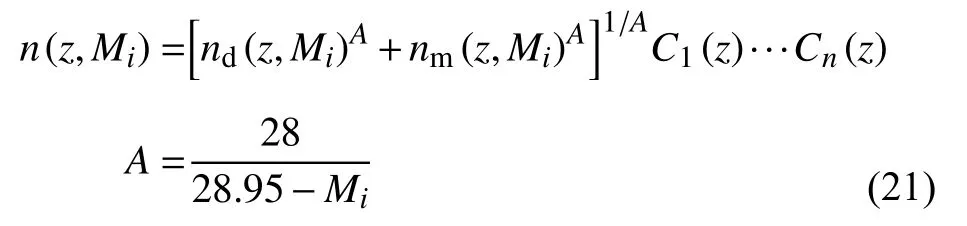
其中nd表示扩散函数，nm为混合函数.参数C1(z)···Cn(z)表示其他修正参数.最后根据大气各成分的相对分子质量Mi，将不同成分质量密度叠加得到大气密度：

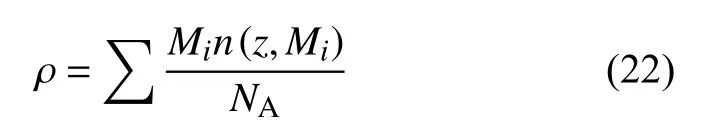
其中NA=6.022×1023mol-1，为阿伏加德罗常数.

MSIS90 版本将该模式的计算高度延展到地面（Hedin, 1991），后来美国海军研究实验室继续开发了NRLMSISE00 版本（Picone et al., 2002），使用的数据包括质谱仪和地基非相干散射雷达观测数据，以及星载加速度计数据、卫星轨道数据反演密度和卫星轨道衰减数据库等，同时还引入了异常氧成分信息.

2.3 DTM 系列模式

DTM（Drag Temperature Model）模式所用建模数据主要为质谱仪、加速度计以及卫星轨道资料反演的大气密度，发展历程和主要情况如表4 所示.本文以DTM-94 模式为例简述其基本算法（Berger et al., 1998）.首先该模式计算了逃逸层温度：

表4 DTM 系列模式基本情况Table 4 Brief introductions of DTM models

不同成分的数密度为：

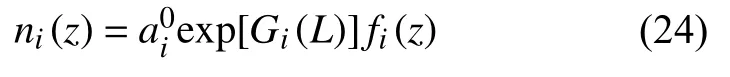
其中，T∞0为常数，代表逃逸层平均温度.a0i表示主要成分在120 km 高度的平均浓度.函数G(L)与MSIS 模式定义相同.fi(z)为基于扩散平衡方程得到的各成分随高度分布曲线.最后叠加所有成分质量密度得到总的大气密度.

2.4 最新版本信息

目前上述三个常见热层大气经验模式最新版本分别为MSIS 2.0、JB2008 和DTM2013，具体信息如表5 所示（Emmert, 2015; 翁利斌, 2019）.

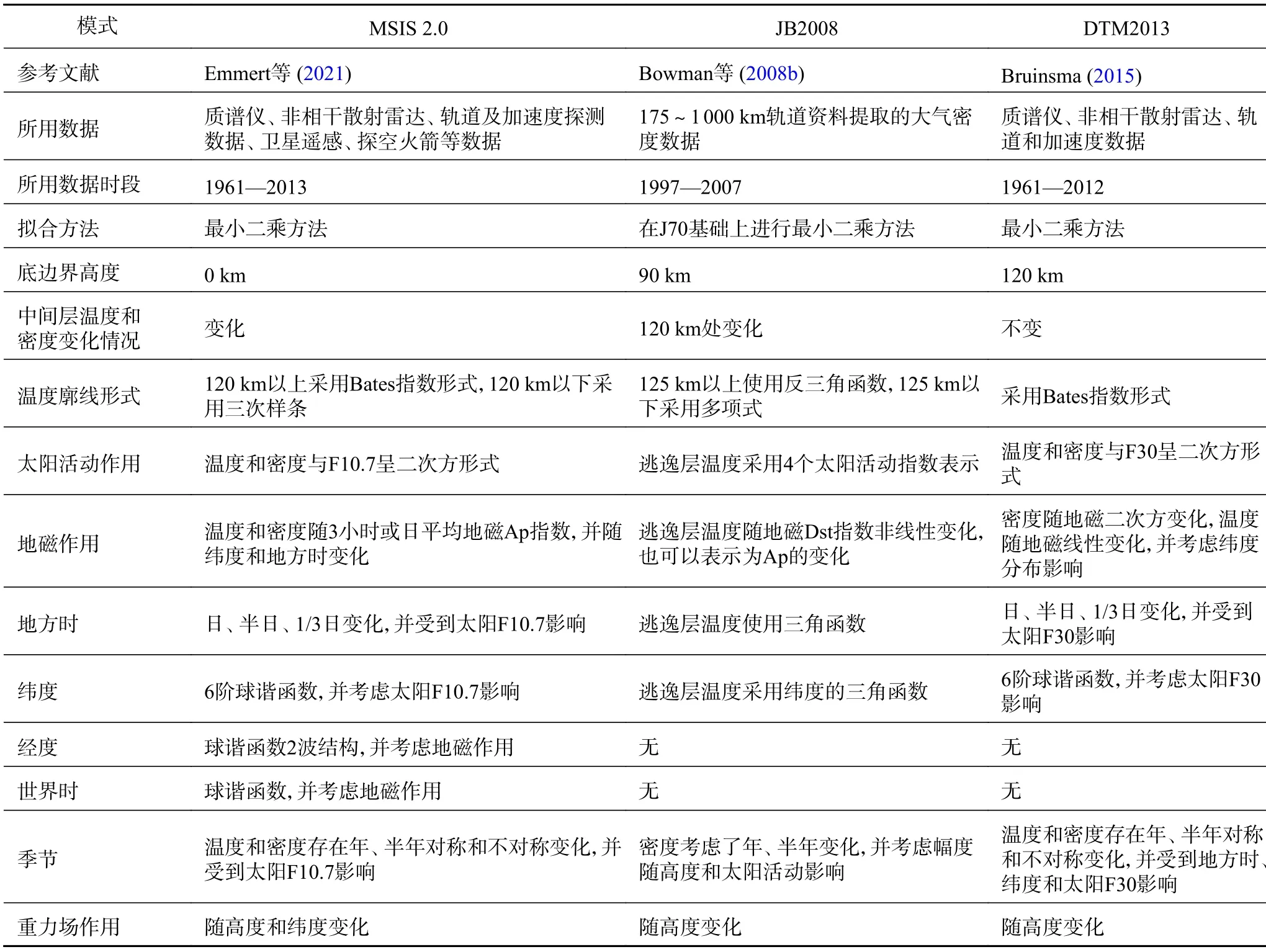
表5 热层大气密度经验模型最新版本信息Table 5 Summary of the selected empirical thermosphere models

3 热层大气模式优化研究进展

随着空间技术的发展，特别是精密定轨及星载高精度加速度计的发展和应用，使用低轨卫星原位探测资料获得了大量高精度大气密度反演数据.近年来基于这些高精度密度探测数据，热层大气模式不断得到优化和发展.本节主要介绍基于高精度探测数据的大气经验模式优化方案.

3.1 热层大气逃逸层温度建模

大部分热层大气经验模式建立在静力平衡假设基础上，一般先计算得到温度，然后根据大气温度与成分的关系获取不同高度大气成分的分布，最终综合所有大气成分获得总的大气密度.在计算大气温度时空分布时，逃逸层温度是一个重要参量，直接影响着大气温度廓线结果.实际的逃逸层温度难以观测，Weng 等（2017）利用热层大气探测密度提取出等效的逃逸层温度，构建了逃逸层温度模型（Exospheric Temperature Model, ETM），利用建模得到的逃逸层温度替代原有经验模型中的逃逸层温度，然后借助MSISE00 计算框架获得热层大气温度、成分和密度信息，从而实现了对一定高度范围内的热层大气密度的修正优化.

3.1.1 逃逸层温度提取

基于热层大气密度探测数据提取逃逸层温度的基本算法是通过不断修正经验模型中的逃逸层温度，使得模式计算的大气密度结果与探测数据一致，则对应的温度即等效逃逸层温度，具体提取流程如图8 所示.图9 展示了基于CHAMP 卫星密度探测数据提取的等效逃逸层温度和MSIS 模式结果的对比，可以看出，经验模式给出的逃逸层温度明显偏高.

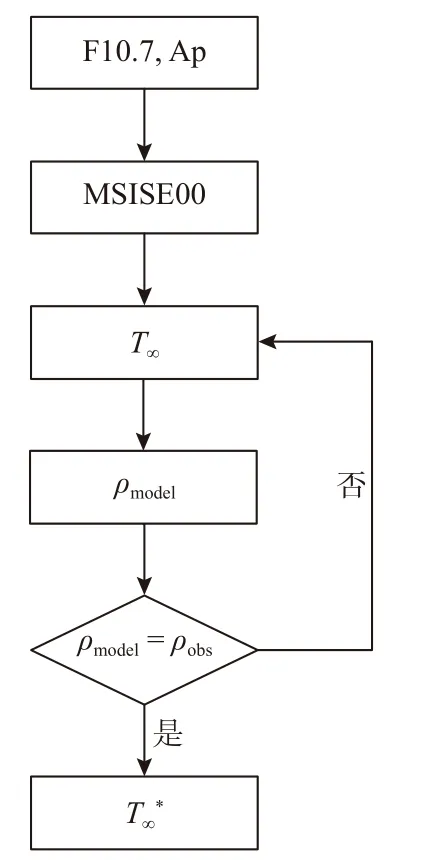
图8 利用MSISE00 经验模式和热层大气密度探测值提取等效逃逸层温度流程图Fig.8 The exospheric temperature derived from MSISE00 and thermospheric density

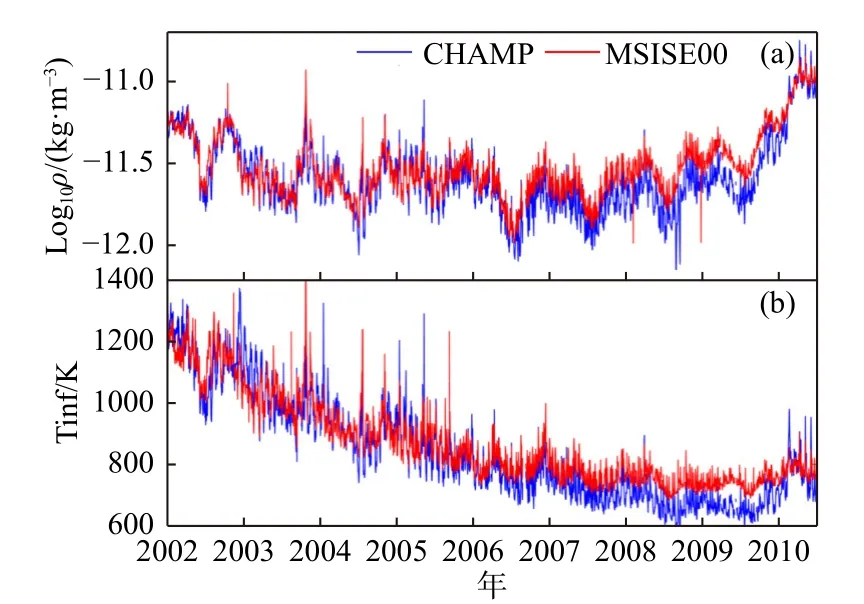
图9 CHAMP 卫星热层大气密度（a）和提取的逃逸层温度（b），以及对应的MSISE00 模式日均值结果Fig.9 Thermospheric density (a) and exospheric temperature(b) derived from CHAMP observation and MSISE00 empirical model

3.1.2 多项式建模方法

考虑到卫星探测数据时空分布、计算效率特别是温度分布特征等因素，Weng 等（2017）在建模时忽略了经度变化的影响，同时加入MSISE00 经验模式的计算结果来约束模式，以保证结果的合理性，并有效解决了稀疏探测数据带来的建模不稳定问题，计算公式如下：

上式中，Tm（m=0, 1, 2, 3）表示：

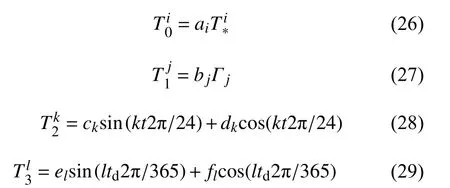
其中，T*为MSISE00 经验模式计算的逃逸层温度结果.

式（27）中：

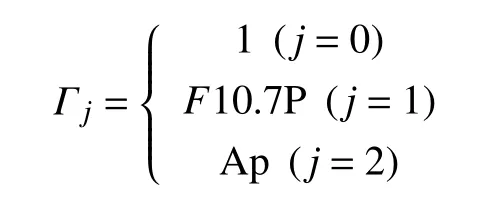
式（28）表示热层大气密度日变化和半日变化，t表示地方时；式（29）表示热层大气密度年变化和半年变化，td表示天数.

3.1.3 逃逸层温度模型结果与分析

最后基于CHAMP 卫星探测数据拟合模型参数.为了独立检验ETM 模式的模拟能力，使用GRACE 卫星大气密度及其提取的逃逸层温度进行对比评估.图10 给出了MSISE00 和ETM 模式模拟的逃逸层温度和热层大气密度与探测值的相对误差统计结果.从图10a 可以看出MSISE00 模式的逃逸层温度结果整体高于GRACE 卫星探测值，偏差和标准差分别为5.88%和6.96%.相比较而言，ETM模式的误差结果基本呈现正态分布，偏差和标准差分别为1.24%和4.29%.图10b 为大气密度与探测值的误差统计结果，可以看出MSISE00 模式模拟的热层大气密度与探测值相对偏差为41.52%，而ETM 模式则为10.58%.经过计算，这两个模式模拟的密度与GRACE 卫星热层大气密度探测值的标准差分别为45.27%和24.75%.由此可见，与MSISE00 模式相比，使用GRACE 数据进行独立检验表明ETM 模式计算得到的逃逸层温度和热层大气密度精度得到了较大幅度提升.

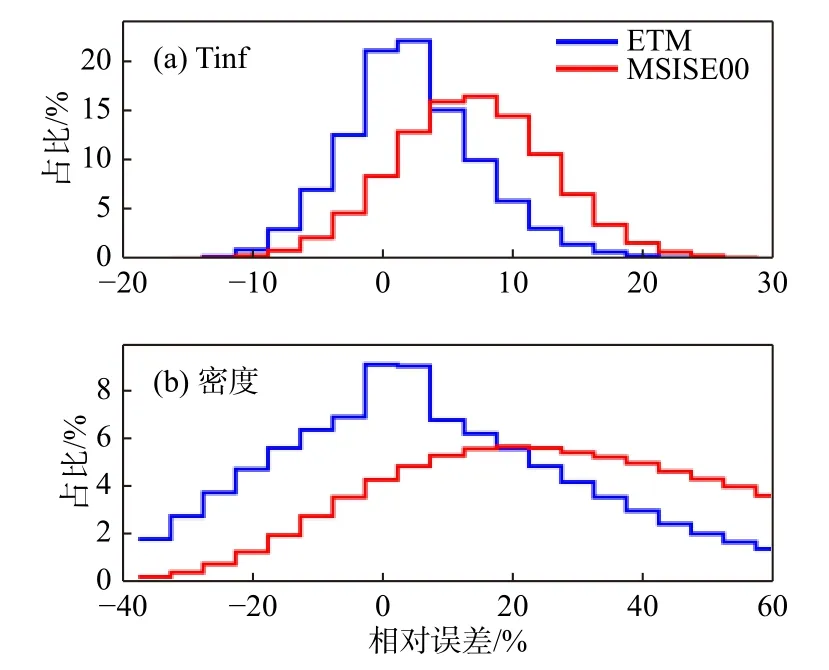
图10 MSISE00 以及ETM 模式模拟的逃逸层温度（a）和GRACE 卫星所在高度热层大气密度（b）与探测值的相对误差统计结果Fig.10 The statistics of relative errors of (a) exospheric temperature and (b) density with GRACE measurements for the ETM (blue line) and MSISE00 (red line)

3.2 热层大气动态修正方案

热层大气动态修正也是模式优化的一种有效方案.其基本原理是融合CHAMP、GRACE 等多源卫星探测数据，结合热层电离层电动力学耦合模型（TIEGCM）模拟结果，构建物理模型+数据驱动的热层大气密度动态修正模式（Ruan et al., 2018）.

3.2.1 基于卫星探测的热层大气密度数据反演逃逸层温度

以静力学平衡条件为依据，热层大气密度的垂直变化可以由热层大气顶部温度和底部温度表征.动态修正的方法是利用经验模式，计算不同大气温度条件下的热层大气密度垂直分布，建立热层大气温度与热层大气密度的定量关系；利用CHAMP、GRACE 等卫星探测的局地热层大气密度，采用迭代方法，获取对应的逃逸层温度，并开展相对应的分析和研究，以完成对热层密度及逃逸层温度信息的收集、处理及其时空分布特征的提取和积累.

3.2.2 基于数值理论模型，提取热层大气正交基函数

热层大气变化的外部驱动源丰富、内部耦合复杂，物理自洽是动态修正的重要考虑因素.根据目前对热层大气的理论研究成果，使用电离层热层耦合模式模拟获取热层大气顶部温度（即逃逸层温度）随太阳和地磁活动水平的时空分布，获取大量的模拟数据源，使用经验正交基方法对数据源进行建模，获取热层大气顶部温度不同模态的时空分布特征，并基于这些模态表征真实大气的变化规律.如图11展示了第一至第五阶正交基函数（PC1-PC5）随纬度与地方时变化的分布图，及其在理论模型数据库中所占比重.

图11 （a-e）第一至第五阶主成分系数（PC1-PC5）随纬度与地方时变化的分布图，（f）及其在理论模型数据库中占所有变化的比重（修改自Ruan et al., 2018）Fig.11 Variations of the basis functions (a-e) PC1-PC5 as a function of local time and latitude and (f) their relative contributions to the total variance (modified from Ruan et al., 2018)

3.2.3 利用稀疏数据驱动技术，构建全球热层大气变化

利用观测数据计算理论模型提取的正交基函数幅度可以有效地将理论模型和实际探测数据结合起来，并实现对热层大气的全球重构.在实际操作中，采用最小二乘法，通过多源卫星探测数据来获取理论模型正交基函数的变化幅度，进而构建全球热层大气变化.图12 为全球热层动态反演示意图.图12a 中蓝色实线代表CHAMP 卫星数据反演的逃逸层温度变化，蓝色虚线代表理论模型模拟的相同位置的逃逸层温度变化，红色实线代表重构结果.从图中可以看到，由于CHAMP 卫星运行轨道的昼夜差异，其探测得到的逃逸层温度也具有显著的高低变化，而理论模型（TIEGCM）能够较好地模拟该变化特征，但具有显著的绝对值差异，因此，理论模型并不能直接用于预测实际大气的变化.与直接的理论模型模拟不同，基于探测数据的重构结果（红线）不仅具有理论模型的变化特征，而且与观测结果具有较好的绝对值一致性，能够满足实际大气预报需求.结果表明，结合理论模型与探测数据，可有效构建全球大气动态模型.

图12 探测数据驱动技术示意图（修改自Ruan et al.,2018）Fig.12 Schematic diagram for the data-driven process (modified from Ruan et al., 2018)

3.2.4 多源卫星数据融合的参数化动态建模

融合CHAMP、GRACE 等多源卫星探测数据，基于理论模型提取的正交基函数及卫星实时探测数据，通过最小二乘法拟合的方式获取正交基函数幅度系数，并对逃逸层温度进行动态反演.Ruan 等（2018）将CHAMP 卫星绕地球每运行一圈所记录的探测数据作为数据驱动源，拟合理论模型构建全球热层大气变化.

参数化过程具体如下：

其中TSG代表太阳活动和地磁活动的作用，TTime代表各正交基系数的年变化和世界时（经度）变化.具体公式如下：

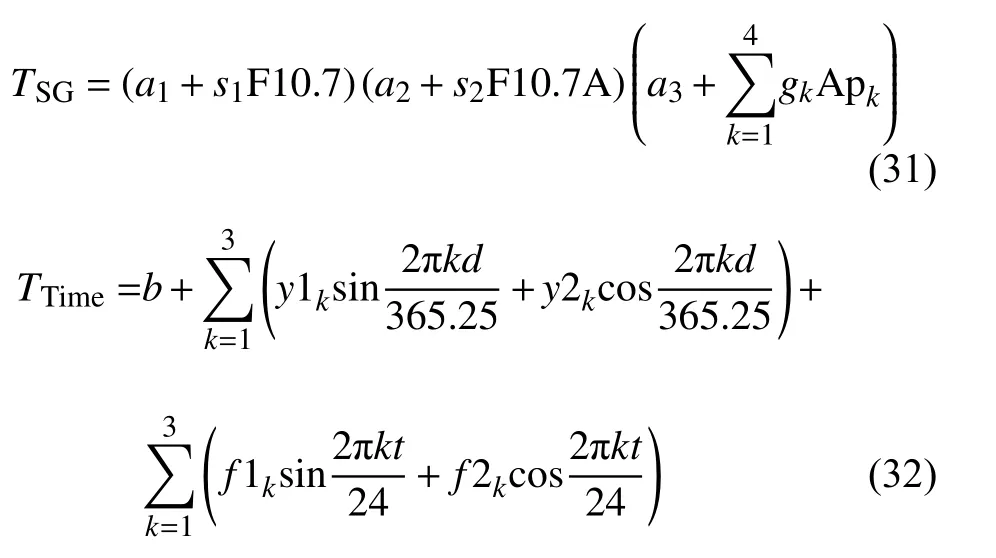
以上F10.7为提前1 天的太阳10.7 cm 射电流量，F10.7A为F10.7 指数81 天滑动平均值，地磁Ap1—Ap4指数分别代表天平均值（Ap1）、提前3 小时的数值（Ap2）、提前6 小时的数值（Ap3）以及提前9 小时的数值（Ap4），d代表年天数，t代表世界时，其余参数可通过最小二乘法拟合获得.

3.3 热层数据同化与预报

3.3.1 数据同化

近年来，数据同化方法在地球科学领域的应用得到快速发展.通过融合探测与模拟信息，数据同化可以提供较观测更完整、较模拟更准确的目标参数状态.三维/四维变分同化（Bannister, 2017）与集合卡尔曼滤波（Evensen, 2003）等方法自提出以来获得了大量关注，且已被广泛应用于气象、海洋和陆面同化系统.

为了更好地估计热层大气温度、密度参数，研究人员发展了一系列热层大气数据同化方法（如,Cantrall et al., 2019; Ruan et al., 2018; Sutton, 2018;Weimer et al., 2020）.Picone 等（2005）及Gondelach和Linares（2020）通过同化基于空间目标轨道跟踪数据（TLE）获得的大气密度信息估计了全球热层大气密度分布.CHAMP 和GRACE 加速度计反演密度也广泛地被应用于热层大气密度同化工作中（ Ren and Lei, 2020; Ruan et al., 2018; Sutton,2018）.常用的同化算法包括集合卡尔曼滤波算法（Codrescu et al., 2018; Matsuo et al., 2013）、集合最优插值方法（Murray et al., 2015）、集合平方根滤波方法（Cantrall et al., 2019）等，用于融合热层观测与经验/理论数值模拟信息.但是，在这些传统同化方法中，为避免观测信息与距离较远处信息的“假相关”，一般通过“局地化”方法对同化过程进行限制，使观测信息仅可调整探测位置附近的大气状态.由于热层探测极为缺乏，如低轨卫星需～1.5 小时获得环绕地球一圈的探测数据，因此传统方法在高层大气数据同化方面具有较大的局限性.

热层作为一个复杂的非线性耦合系统，其时空演化依赖于各种参数的协同作用，如温度、风、密度以及中性组分.由于热层大气环流模型（GCM）可以较好地模拟高层大气不同时空尺度的复杂变化，因此考虑基于理论模式的数据同化可以提供对热层更好的预测与预报能力.Ren 和Lei（2020）利用CHAMP 卫星轨道密度探测，迭代调整热层大气环流模型中太阳与地磁驱动指数，从而使模拟与探测的轨道密度一致，构建了基于理论模式的热层数据同化系统PIDA.他们进一步使用GRACE 卫星轨道密度和GUVI 临边观测对PIDA 进行评估.比较结果显示，PIDA 同化结果与CHAMP 轨道密度非常一致.然而，通过与轨道高度较高的GRACE 卫星轨道密度以及TIMED-GUVI 临边观测进行对比，结果显示PIDA 可以很好地估计全球热层密度的时空演化，但该同化密度存在高度依赖的系统偏差.

图13a、13c 展示了GUVI 临边观测以及TIEGCM 和PIDA 估计的平均温度与密度剖面，相应的模拟与观测比值的统计平均在图13b、13d 中给出.可以看出，与TIEGCM 模型对比，同化后的热层大气密度与观测结果更为吻合，而同化后的温度偏差增大.主要原因是，Kp 与F10.7 的变化主要影响高热层的状态，通过调整PIDA 模型外驱动参数以符合卫星轨道密度探测的方法，无法对低热层（低于150 km）状态产生显著影响.因此，为了与CHAMP 轨道密度相一致，PIDA 模型低估了热层大气温度，使得热层大气标高相应降低.由于温度的变化对热层密度的影响会在高度上持续累计，从而导致PIDA 同化后的热层密度在低高度比真实情况偏高，而在更高的高度比探测结果偏低.

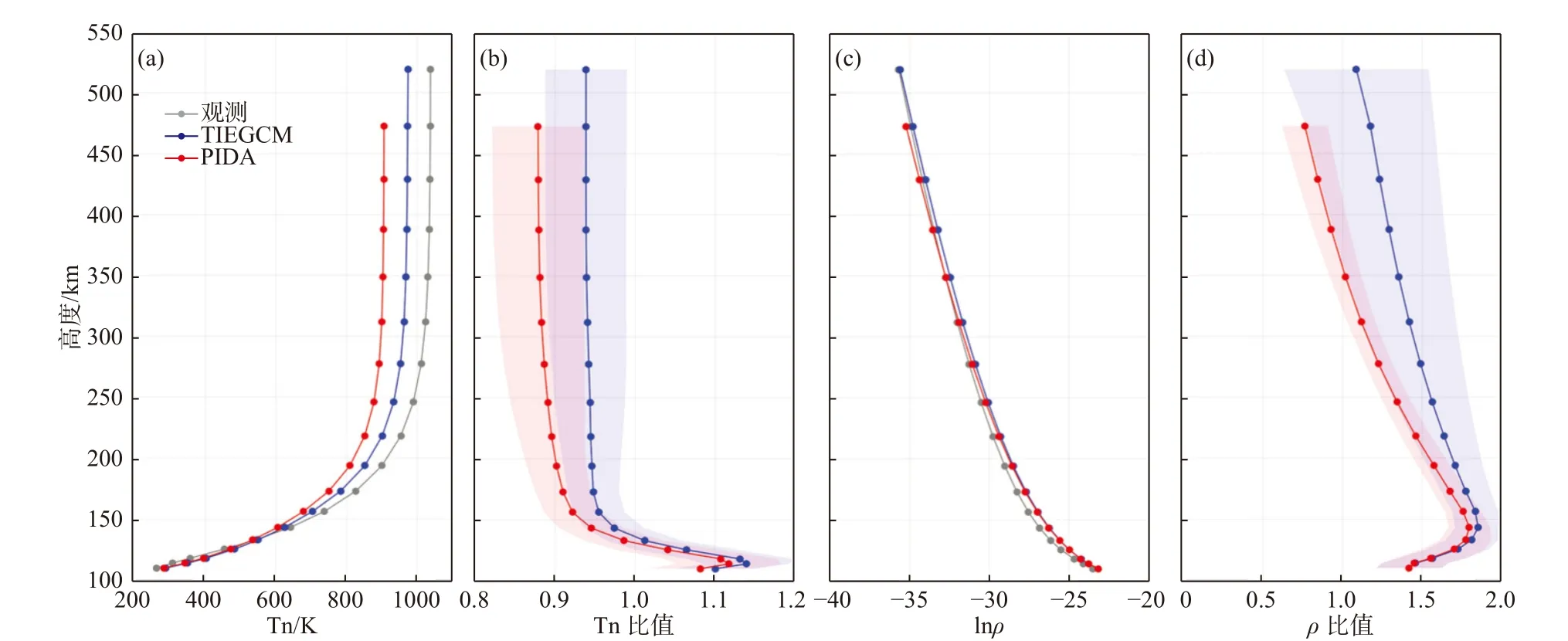
图13 2004年第80—280 天平均的GUVI 临边观测（a）温度与（c）密度高度剖面（灰色：观测；蓝色：TIEGCM；红色：PIDA）.（b）温度与（d）密度的模拟与观测比值的统计平均（蓝色：TIEGCM；红色：PIDA）.统计标准差由图（b）和图（d）中相应的彩色阴影表示（修改自Ren and Lei, 2020）Fig.13 The altitude profiles of the temporal and spatial averaged (a) temperature and (c) density from Limb observations (gray dotted lines) and the corresponding simulation results from TIEGCM (blue dotted lines) and PIDA (red dotted lines).The mean ratio of the simulation results (blue line for TIEGCM; red line for PIDA) to observations for (b) temperature and (d) density.The standard deviations were marked by the corresponding colored shading in (b) and (d) (modified from Ren and Lei, 2020)

在流体静力学条件下，热层密度的高度分布与热层底边界的密度和温度显著相关.结果显示，TIEGCM 明显高估了低热层的温度以及密度.尽管F10.7 与Kp 可以显著影响高热层状态，但是其变化无法对低热层大气产生显著影响.因此，理论模式对低热层估计的较大偏差使得PIDA 对不同高度密度的估计仍存在较大偏差.因此，基于理论模式的数据同化系统应同时考虑低热层大气的状态估计.此外，研究还指出，热层数据同化需融合不同高度的多种参数信息，以消除同化系统偏差.

3.3.2 基于智能优化算法的热层预报研究

在传统的高层大气数值预报应用中，一般先通过特定数据同化方法，对实时热层大气状态（如质量密度、温度和中性成分等）进行尽可能准确地估计.然后，使用预报模式对热层大气状态进行预报.由于高层大气理论模式可以重现不同时空尺度下复杂的热层大气变化特性，其通常被选用为预报模式.但是，由于模式中的某些缺陷（如不确定性参数、缺少物理过程等）以及太阳与地磁活动预测困难等限制，理论模式预报误差会随时间迅速增大，从而导致有效预报时长局限在几天之内.对热层大气长期可靠的预报仍是科学界挑战性的难题之一.

Ren 和Lei（2022）构建了一种新型的基于全球探测的热层预报模式GOFT，以实现热层大气数十天的稳定预报.GOFT 使用TIEGCM 作为基本理论模式.GOFT 通过智能优化粒子滤波算法，对TIEGCM 中可能导致热层状态估计显著误差的一系列不确定性参数进行智能调整，实现了热层大气预报.他们利用TIEGCM 以及广泛使用的热层经验模式MSISE00 与GOFT 预报结果进行对比.结果表明，在太阳和地磁活动给出的情况下，GOFT 可提供可靠的超30 天预报.此外，基于GOFT 有望实现复杂的非线性耦合高层大气系统的长期预报.

基于智能优化粒子滤波算法的热层预报模式GOFT 逻辑示意图如图14 所示.粒子滤波是非线性非高斯系统状态估计的常用数据同化算法（如，Djuric et al., 2003; van Leeuwen, 2009）.GOFT 模式粒子群组中“粒子”为不确定性参数被随机扰动后的TIEGCM 模式.在当前版本调整了12 个对热层状态存在显著影响的不确定性参数（如潮汐、焦耳加热因子等）.GOFT 首先在每个时间步将粒子更新一定的时长.然后根据模拟-观测误差获得每个粒子权重.这些权重粒子便用于热层预报.为了获得更优的粒子群，在下一步同化新的观测之前，通过特定的智能优化算法对模式不确定参数（即粒子群中的粒子）进行选择变异.

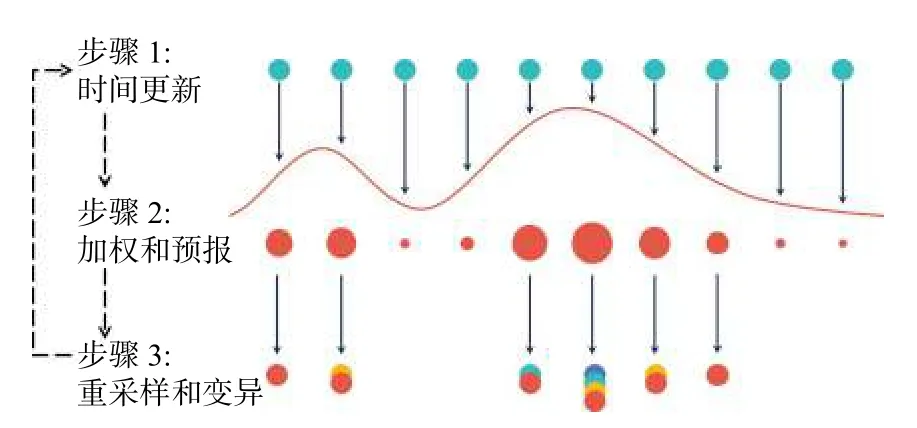
图14 预报模式GOFT 示意图.彩色圆点表示GOFT 中的粒子，其大小与粒子权重成正比.红色曲线表示概率密度函数（修改自Ren and Lei, 2022）Fig.14 Schematic view of the forecast model GOFT.The solid dot symbols indicate the particles in the GOFT with the symbol sizes proportional to the weighting of the particles.The red curve represents the probability density function (modified from Ren and Lei, 2022)

GOFT 模式的关键目标是提供较现有模型更为可靠的热层长期预报.图15 比较了GOFT 和TIEGCM 对GUVI 临边密度的30 天预报误差.如图15a 所示，在前15 天预报时段内，GOFT 对390 km 高度轨道密度的预报误差低于15%，相较于TIEGCM 的预报误差分别提高了90%.此外，我们还与热层经验模型MSISE00 预报结果进行比较，对比结果显示GOFT 预报精度同样提高了80%.在后续15 天预报时段，GOFT 对GUVI 临边密度的预报误差仍低于20%，与TIEGCM 相比提高了～80%～90%，而与MSISE00 相比提高了20%～70%.评估结果表明，预报模式GOFT 对热层质量密度的30 天预报精度比理论模式TIEGCM 提高了70%～90%.该方法为复杂的高层大气预报系统提供了未来的改进前景.需要指出的是，GOFT 对热层的预报需要提供F10.7 和Kp 指数预报，这里使用了真实的Kp 与F10.7 指数以评估GOFT 在预测热层方面的性能.

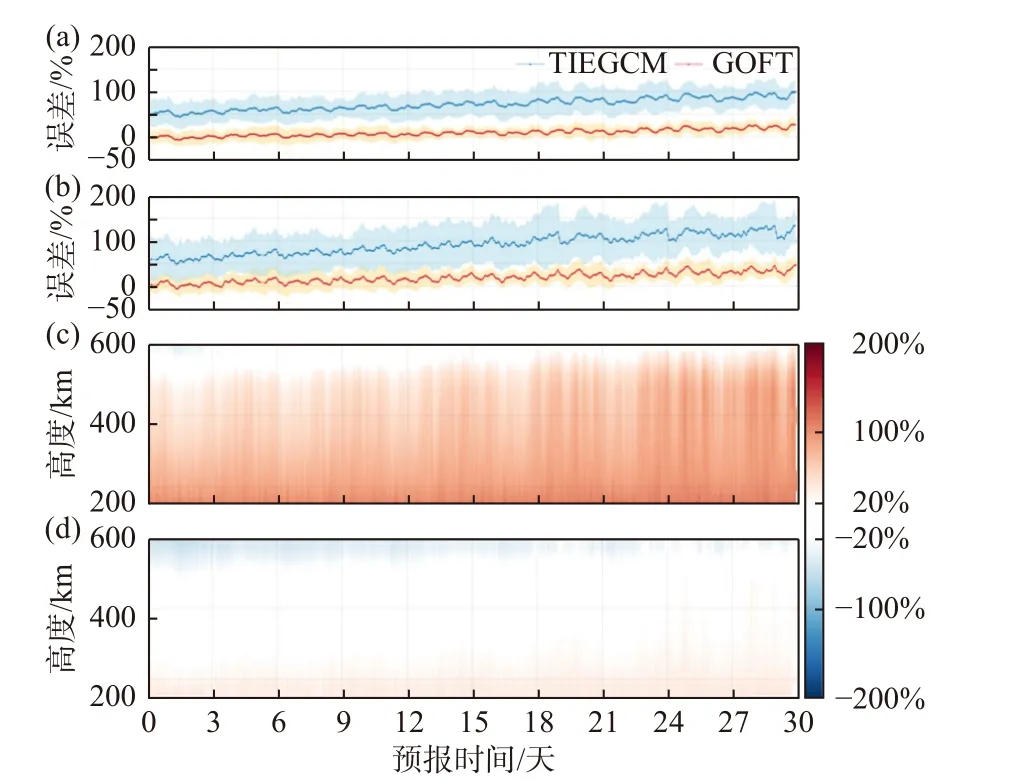
图15 GOFT（红色点线）和TIEGCM（蓝色点线）对（a）CHAMP 和（b）GRACE 轨道平均密度的30 天平均预报误差随预报时长的变化.阴影表示统计标准差.（c）TIEGCM 和（d）GOFT 对150～600 km轨道平均临边密度的30 天预报误差随预报时长和高度的变化（修改自Ren and Lei, 2022）Fig.15 Statistical results for the 30-day forecast from the GOFT and TIEGCM.The GOFT (red line) and TIEGCM (blue line) averaged relative forecasting errors with the standard deviations (corresponding colored shading) for the orbital mean mass density from(a) CHAMP and (b) GRACE satellites during the 30-day forecast interval.The statistical average of the relative forecasting errors for limb orbital mean mass density by TIMED-GUVI from the (c) TIEGCM and (d)GOFT (modified from Ren and Lei, 2022)

4 热层大气响应典型空间事件特征研究进展

热层大气对空间事件的响应是当前热层研究的热点.在一些突发空间事件中，例如磁暴、耀斑、日食等，热层大气通常表现出短时间尺度的变化特征.早期关于磁暴期间热层大气的响应特征研究主要源于对空间目标轨道跟踪数据的分析，Jacchia（1959b）基于Sputnik 3 轨道数据首次证实了磁暴会造成热层大气密度的显著增长（图16）.近年来随着星载加速度计的应用，高时空分辨率的大气密度观测数据揭示了更多热层大气在磁暴期间的精细变化特征（Bruinsma et al., 2006; Lei et al., 2011,2012; Liu et al., 2010, 2011; Lühr et al., 2004; Sutton et al., 2005）.图17 展示了CHAMP（400 km）和GRACE（490 km）卫星观测到的2003年11月19—21日磁暴期间热层大气在不同高度上的变化特征.磁暴期间，极区附近热层大气密度迅速增加，随后极区附近的密度增强区域开始向赤道传播，大约4 个小时后赤道附近大气密度增加.CHAMP 观测表明南北半球大气响应较为对称，而GRACE 则观测到热层大气在南半球的响应强于北半球，因此热层大气对磁暴响应的半球不对称性可能存在高度和地方时相关性（Li and Lei, 2021b）.从全球尺度而言，磁暴期间热层大气密度增加了300%～800%.磁暴导致的大气密度增强会加剧航天器轨道衰减.极端磁暴条件下，航天器轨道衰减率会增大至平静时期的8 倍，中等强度磁暴也会造成轨道衰减率100%～150%的增加（Li and Lei, 2021a）.另外，共转相互作用区（CIR）驱动的地磁扰动虽然强度弱，但是持续时间较长，因而也会对卫星轨道造成显著影响（Chen et al., 2012, 2014）.磁暴结束后，热层大气进入恢复阶段，Lei 等（2012）基于CHAMP 和GRACE 卫星观测资料指出，由于NO恢复速度较慢，NO 的冷却效应会导致热层大气在磁暴结束后出现“过冷却”效应，磁暴结束后的热层大气密度可能低于磁暴之前平静时期水平（图18）.

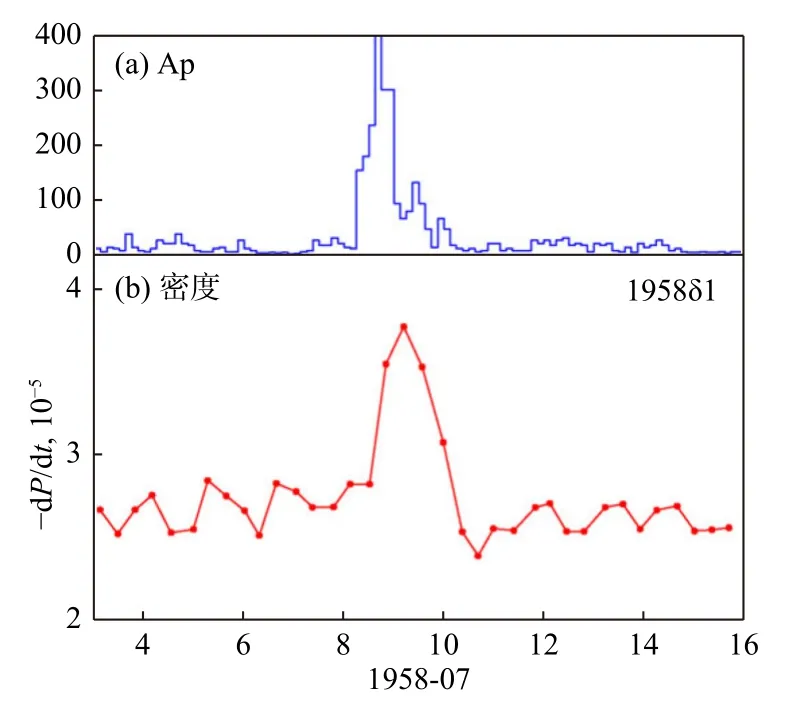
图16 1958年7月磁暴期间的Ap 指数变化（a），以及空间目标1958 δ1（SPUTNIK 3 rocket）运行周期变化率（b）.航天器轨道周期变化率可以表征大气密度的变化（修改自Prölss, 2011）Fig.16 Ap index (a) and the orbit period change rate of space object 1958 δ1 (b) during geomagnetic storm in July,1958.The change rate of the space object represents the orbital density (modified from Prölss, 2011)

图17 CHAMP（a, b）和GRACE（c, d）卫星观测到的热层大气对2003年11月20日磁暴的响应（修改自Bruinsma et al.,2006）Fig.17 The thermospheric response to 20 November, 2003 geomagnetic storm observed by CHAMP (a, b) and GRACE (c, d) satellites (modified from Bruinsma et al., 2006)

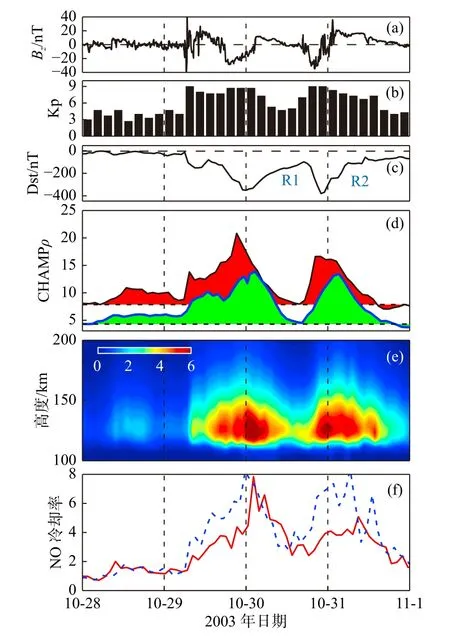
图18 2003年10月28—31日磁暴期间（a）行星际磁场Bz 分量、地磁（b）Kp、（c）Dst 指数，（d）归一化至390 km 高度的CHAMP 卫星白天（红色）和夜晚（绿色）轨道平均密度，（e）基于TIMED/SABER 观测的100～200 km 高度上NO 冷却率的轨道平均，以及（f）125 km 高度上白天（红色）、夜晚（蓝色）的NO 平均冷却率.其中密度单位为10-12 kg/m3.图（d）中虚线表示最平静时期的大气密度；NO 冷却率单位为107 erg/cm3/s（修改自Lei et al., 2012）Fig.18 Variations of (a) interplanetary magnetic field Bz, geomagnetic (b) Kp and (c) Dst indices, (d) dayside (red)and nightside (green) orbital averaged densities from CHAMP (normalized to 390 km), orbital averaged NO cooling rate from TIMED/SABER (e) between 100 and 200 km, and (f) dayside (red) and nightside (blue) averaged NO cooling rates at 125 km during 28-31 October 2003.Note that the mass densities in (d) are in units of 10-12 kg/m3, and the dashed lines stand for mass densities during the quietest period on October 28; NO cooling rates in (e-f) are in units of 107 erg/cm3/s (modified from Lei et al., 2012)

太阳耀斑爆发，伴随着太阳EUV 辐射的突然增强，导致低热层加热效应增加，热层大气随即膨胀.CHAMP 卫星观测显示，在2003年10月28日X17 级耀斑事件中，400 km 高度上热层大气密度增加了30%～40%，响应时间约为1～3 小时（Liu et al., 2007; Pawlowski and Ridley, 2008; Sutton et al.,2005）.

日全食发生时，月影区EUV 辐射迅速降低至接近0，导致月影区热层温度下降，密度降低.研究人员通过理论模式模拟了日食期间热层大气的演化特征（Dang et al., 2018; Harding et al.2018; Lei et al., 2018）.Li 等（2021）进一步通过多颗卫星联合观测，证实了日食不仅会造成月影区10%～25%的局地大气密度扰动，还会以波动的形式对全球热层大气造成持续性影响（图19）.

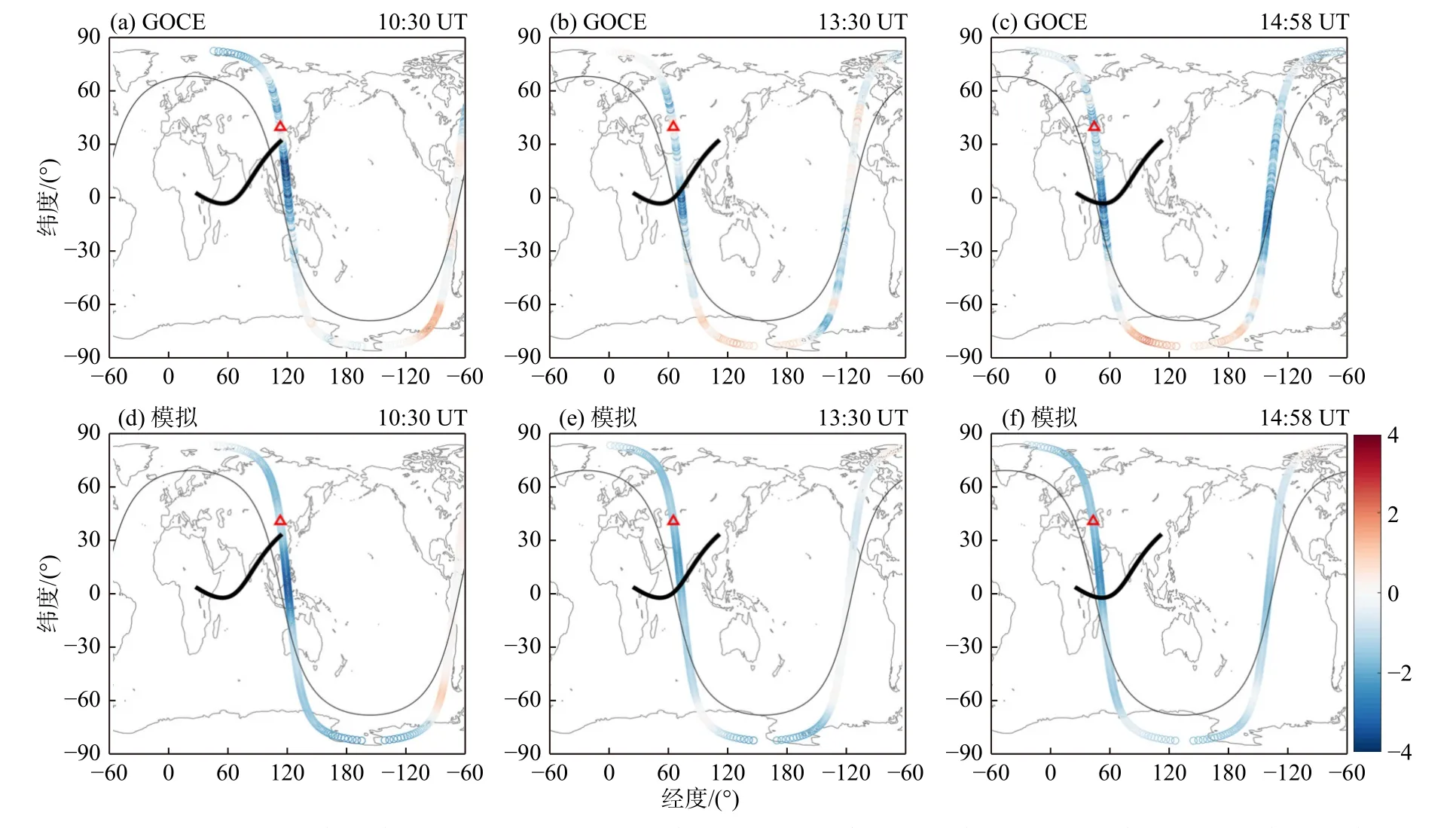
图19 2010年1月15日日食结束后GOCE 卫星轨道密度相对背景密度的绝对变化.背景密度定义为日食前8 个轨道的平均密度.密度单位为10-12 kg/m3.图（a-c）表示观测密度；（d-f）表示模拟结果.红色三角形代表卫星位置，右上角时间为当前时间（修改自Li et al., 2021）Fig.19 The absolute changes of neutral densities after the 15 January 15, 2010 solar eclipse with respect to the background density from (a-c) GOCE observation and that (d-f) from TIE-GCM simulation.Note that the densities are in units of 10-12 kg/m3 and the background density is defined as the mean density of eight orbits before the eclipse.The red triangles stand for satellite positions at the specific times shown in the top right-hand corner of each column (modified from Li et al., 2021)

5 总结

热层是日地空间系统重要的组成部分，一方面，研究热层对于理解整个日地空间因果链上的相互作用具有重要的科学意义；另一方面，由于人类大部分的空间活动都在热层，掌握热层大气变化规律，构建并优化热层大气模式对于保障太空资产和空间活动安全、确保航天航空任务的圆满完成具有显著的工程应用价值.

本文介绍了当前热层大气密度反演的方法，比对了各种方法的优缺点.TLE 数据具有跟踪目标数量多、观测持续时间长等优势，但观测时间精度相对较低，因而TLE 反演密度在热层大气气候学研究以及模式标定领域具有一定优势；基于精密轨道数据可以反演获得较高分辨率和精度的大气密度观测结果，且在携带星载加速度计的情况下可用于标定加速度计数据；加速度计数据反演密度具有最高的时空分辨率和精度.

随着观测技术的发展，基于最新的观测数据，热层大气模式优化工作已取得了长足的进展.使用加速度计数据反演密度修正逃逸层温度时，采用多项式或者稀疏矩阵拟合等技术取得了较好的优化效果.此外，多源参数同化以及粒子滤波等技术也开始应用于热层大气模式优化研究中，推动了热层大气密度中长期预报的研究进展.热层大气研究虽然取得了诸多成果，但其数据的时空覆盖依旧贫乏，热层变化特性尚需进一步探索和认识.目前的大气模式精度也有待进一步提高，还需要发展更多的新方法、新技术应用于热层大气研究和应用，以提升我们对热层的认识，并服务于卫星轨道定位与预报等.